双指针算法
1.基本介绍
严格的来说,双指针只能说是是算法中的一种技巧。
双指针指的是在遍历对象的过程中,不是普通的使用单个指针进行访问,而是使用两个相同方向(快慢指针)或者相反方向(对撞指针)的指针进行扫描,从而达到相应的目的。最常见的双指针算法有两种:一种是,在一个序列里边,用两个指针维护一段区间;另一种是,在两个序列里边,一个指针指向其中一个序列,另外一个指针指向另外一个序列,来维护某种次序。
2.模板
for (int i = 0, j = 0; i < n; i ++ ) // j从某一位置开始,不一定是0
{
while (j < i && check(i, j)) j ++ ;
// 具体问题的逻辑
}
常见问题分类:
(1) 对于一个序列,用两个指针维护一段区间,比如快排的划分过程
(2) 对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作
双指针算法的核心思想(作用):优化
在利用双指针算法解题时,考虑原问题如何用暴力算法解出,观察是否可构成单调性,若可以,就可采用双指针算法对暴力算法进行优化.
当我们采用朴素的方法即暴力枚举每一种可能的情况,时间复杂度为O(n*n)
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
//具体逻辑
}
}
而当我们使用双指针算法时通过某种性质就可以将上述O(n*n)的操作优化到O(n)
暴力算法和它优化后的双指针算法有什么区别:
由于具有某种单调性,朴素算法往往能优化为双指针算法。
区别:
- 朴素算法每次在第二层遍历的时候,是会从新开始(j会回溯到初始位置),然后再遍历下去。(假设i是终点,j是起点)
- 双指针算法:由于具有某种单调性,每次在第二层遍历的时候,不需要回溯到初始位置(单调性),而是在满足要求的位置继续走下去或者更新掉。
3.例题
例题01、
先看这样一个例子:输入一个字符每个子串之间有一个空格,让你输出每一个空格后的子串。
输入
abc def hij输出
abc def hij
【参考代码】
#include<iostream>
#include<string>
using namespace std;
int main()
{
string str;
getline(cin, str);
int n = str.size();
for(int i = 0; i < n; i++)
{
int j = i;
while(str[j] != ' ') j++;
// cout<<j;
for(int k = i; k < j; k++) cout<<str[k];
cout<<endl;
i = j; //循环体执行完后for()中的i才 i++即,下一次开始时 i就到了上一次空格(位置j)的下一位
}
return 0;
}
例题02、
【AcWing 799. 最长连续不重复子序列 】
给定一个长度为 n 的整数序列,请找出最长的不包含重复的数的连续区间,输出它的长度。
输入格式
第一行包含整数 n。
第二行包含 n 个整数(均在 0∼105 范围内),表示整数序列。
输出格式
共一行,包含一个整数,表示最长的不包含重复的数的连续区间的长度。
数据范围
1≤n≤105
输入样例:
5
1 2 2 3 5输出样例:
3
思路:
使用双指针算法,根据观察发现,当使用i,j两个快慢指针表示当前的指针移动到i的最长不重复序列时候,具有单调性,即i向后移动,j必然向右或者不动,不可能向左移动,这一单调性质导致可以使用双指针算法。(当你出现重复时若j还向左移动,那序列必然还有重复,这就矛盾了!)
在双指针算法中,一个指针扫描整个数组而移动,关键如何找到对应的另一个指针移动的位置,在本题中,我们定义i为块指针,j为慢指针,j的位置定义为i对应的最长不重复序列的j的位置,因为不重复,i和j元素都不重复,出现次数都为一,因此我们使用一个数组s来记录各个元素出现的次数,i,j不断移动,数组及时更新,每次i更新,便更新j确保(j,i)区间元素都只出现一次,代码如下
【参考代码】
#include<iostream>
using namespace std;
const int N = 100000+10;
int a[N],s[N];// s[N]用来记录数据出现的次数
int main()
{
int n;
cin>>n;
int res = 0;
for(int i = 0; i < n; i++) cin>>a[i];
for(int i = 0, j = 0; i < n; i++)
{
// 注意:j = 0不能拿下来,不然每次又是从0开始了!
s[a[i]]++; // 记录数值a[i]出现的次数
// i快指针,j 慢指针
while(j <= i && s[a[i]] > 1) // 若出现重复的数值。j <= i不要也行
{
s[a[j]]--;
j++;
}
//更新的不包含重复的数的连续区间的最大长度
res = max(res, i - j +1);
}
cout<<res;
return 0;
}
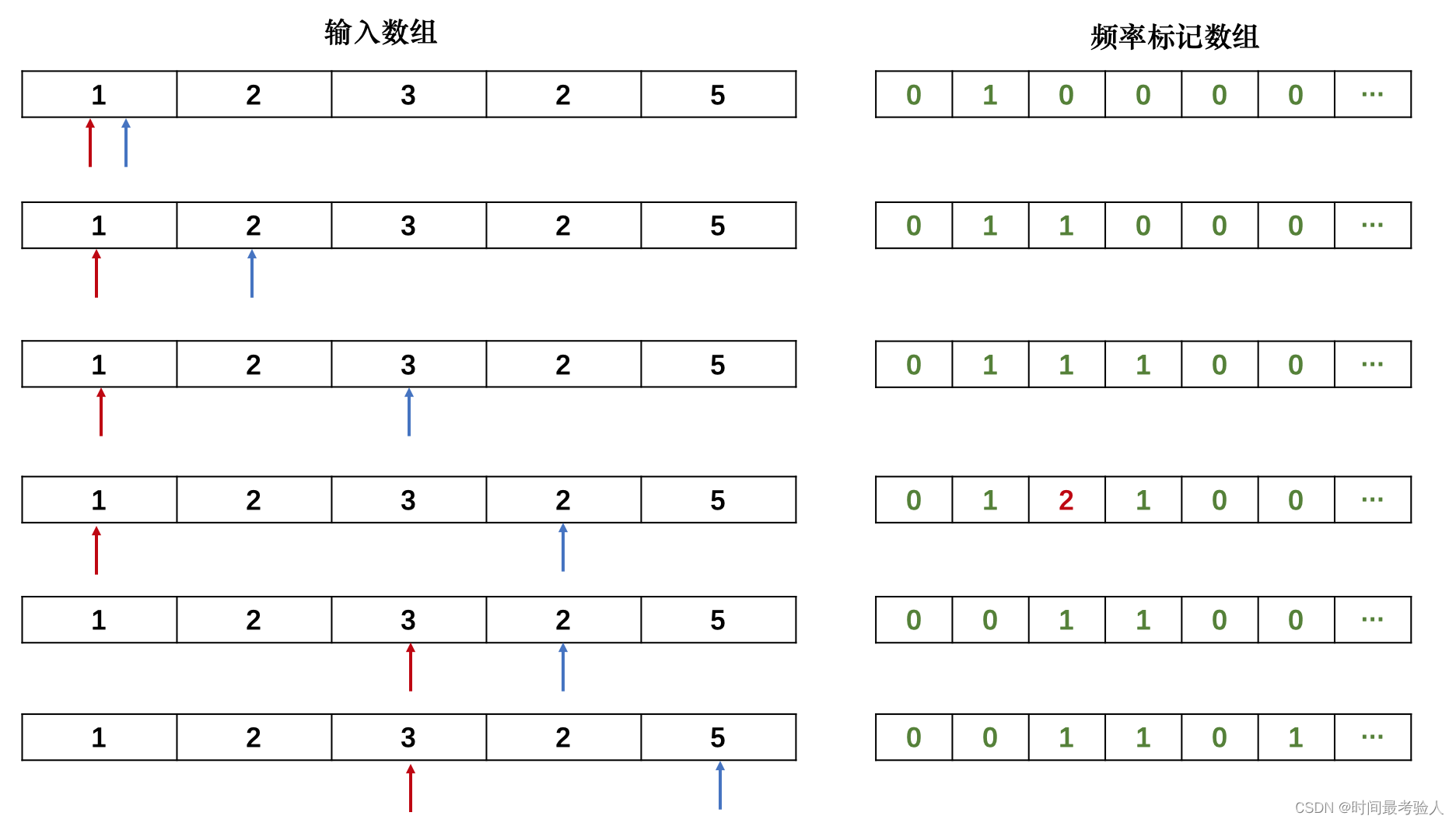
图解辅助理解:
例题03、
【acwing 800.数组元素的目标和】
给定两个升序排序的有序数组 A 和 B,以及一个目标值 xx。
数组下标从 0开始。
请你求出满足 A[i]+B[j]=x 的数对 (i,j)(i,j)。
数据保证有唯一解。
输入格式
第一行包含三个整数n,m,x,分别表示 A 的长度,B 的长度以及目标值 x。
第二行包含 n 个整数,表示数组 A。
第三行包含 m 个整数,表示数组 B。
输出格式
共一行,包含两个整数 i 和 j。
数据范围
数组长度不超过 105。
同一数组内元素各不相同。
1≤数组元素≤109输入样例:
4 5 6
1 2 4 7
3 4 6 8 9输出样例:
1 1
【暴力做法】O(n*n)
#include<iostream>
using namespace std;
const int N = 100000+10;
int a[N],b[N];
int main()
{
int n,m,x;
cin>>n>>m>>x;
for(int i = 0; i < n; i++) scanf("%d",&a[i]);
for(int i = 0; i < m; i++) scanf("%d",&b[i]);
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(a[i]+b[j] == x)
{
cout<<i<<" "<<j<<endl;
}
}
}
return 0;
}
【双指针算法】O(n + m)
思路:
- 双指针算法的核心思想是优化,因此可以先写出暴力做法
- 寻找单调性,双指针算法进行优化
通过暴力法我们可以知道,对于每一个i都想找到一个j使得a[i]+b[j]==x,由于两段序列都是单调递增的,具有单调性,因此我们可以用双指针算法进行优化。
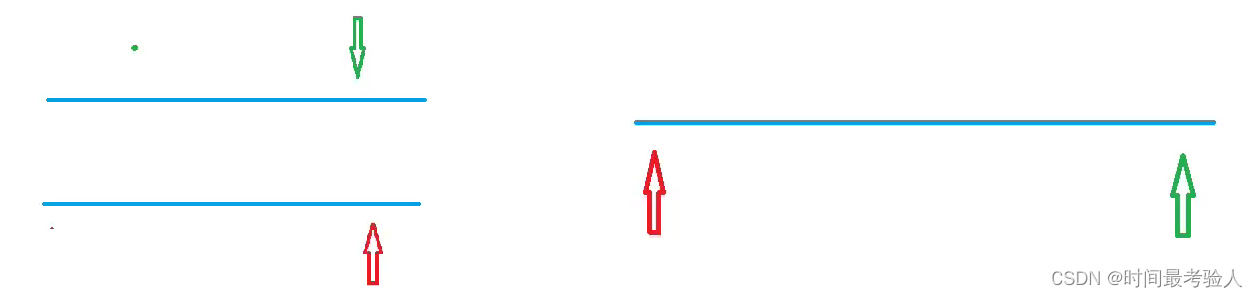
我们让j从m-1位置开始(从右往左扫描),根据单调性,一旦a[i] + b[j] > x,当前i位置的下一个a[i]:必定会有a[i] + b[j] > x,那么j就左移j--。当出现a[i] + b[j] == x时输出结果即可。注:j是从下标m-1位置开始往左移的,即还要满足j>=0。
#include<iostream>
using namespace std;
const int N = 100000+10;
int a[N],b[N];
int main()
{
int n,m,x;
cin>>n>>m>>x;
for(int i = 0; i < n; i++) scanf("%d",&a[i]);
for(int i = 0; i < m; i++) scanf("%d",&b[i]);
for(int i = 0, j = m - 1; i < n; i++)
{
while(j >= 0 && a[i] + b[j] > x) j--;
if(a[i] + b[j] == x)
{
printf("%d %d\n", i, j);
break;
}
}
return 0;
}
例题04、
【acwing 2816. 判断子序列】
给定一个长度为 n 的整数序列 a1,a2,…,an 以及一个长度为 m 的整数序列 b1,b2,…,bm。
请你判断 a 序列是否为 b 序列的子序列。
子序列指序列的一部分项按原有次序排列而得的序列,例如序列 {a1,a3,a5} 是序列 {a1,a2,a3,a4,a5} 的一个子序列。
输入格式
第一行包含两个整数 n,m。
第二行包含 n 个整数,表示 a1,a2,…,an。
第三行包含 m 个整数,表示 b1,b2,…,bm。
输出格式
如果 a 序列是 b 序列的子序列,输出一行
Yes。否则,输出
No。数据范围
1≤n≤m≤1051≤n≤m≤105,
−109≤ai,bi≤109−109≤ai,bi≤109输入样例:
3 5
1 3 5
1 2 3 4 5输出样例:
3 5
1 3 5
1 2 3 4 5
思路:
- 判断子序列,顺次判断!
j指针用来扫描整个b数组,i指针用来扫描a数组。若发现a[i]==b[j],则让i指针后移一位。- 整个过程中,
j指针不断后移,而i指针只有当匹配成功时才后移一位,若最后若i==n,则说明匹配成功。
【参考代码】
#include<iostream>
using namespace std;
const int N = 100000+10;
int a[N],b[N];
int main()
{
int n,m;
scanf("%d%d", &n, &m);
for(int i = 0; i < n; i++) scanf("%d",&a[i]);
for(int i = 0; i < m; i++) scanf("%d",&b[i]);
int i = 0, j = 0;
while(i < n && j < m)
{
//i只有在匹配成功时才往后移动一位,而j在整个过程中要不断扫描
if(a[i] == b[j])
{
i++;
j++;
}
else j++;
}
// 最后i == n说明匹配成功
if(i == n) puts("Yes");
else puts("No");
return 0;
}
上述14~24行代码也可以改成:
//j在整个过程中要不断扫描,而i只有在匹配成功时才往后移动一位
int i = 0;
for(int j = 0; j < m; j++)
{
if(i < n && a[i] == b[j]) i++;
}
【总结】
针对板子里while什么情况下使用?
当我们遇到像 AcWing 799.最长连续不重复子序列,AcWing 800.数组元素的目标和 这种问题,我们需要先固定一个指针,然后另一个指针去连续的判断一段区间,需要while()循环。换句话说,
while()循环用来解决连续一段区间的判断问题,而这道题中我们需要对a数组和b数组的每一位,逐位去进行比较判断,j指针不断后移,而i指针只有当匹配成功时才后移一位,它不是连续一段区间的判断。更重要的还是灵活变通!
例题05、
【acwing 32. 调整数组顺序使奇数位于偶数前面】
输入一个整数数组,实现一个函数来调整该数组中数字的顺序。
使得所有的奇数位于数组的前半部分,所有的偶数位于数组的后半部分。
样例
输入:[1,2,3,4,5]
输出: [1,3,5,2,4]
思路:类似于快速排序的划分过程
题目要求:调整数组顺序使奇数位于偶数前面。
- 前段:定义
i指针从头开始遍历扫描,如果是奇数则指针右移i++,一旦出现偶数则停止 - 后段:定义
j指针,从右往左遍历扫描,如果是偶数则指针左移j--,一旦出现奇数则停止 - 在
i < j情况下交换停止时的奇偶数,然后接着下一次循环,直到i=j时循环结束
【参考代码】
class Solution {
public:
void reOrderArray(vector<int> &array) {
int i = 0, j = array.size() - 1;
while(i < j)
{
while(i < j && array[i] % 2 == 1) i++;
while(i < j && array[j] % 2 == 0) j--;
if(i < j) swap(array[i], array[j]);
}
}
};
总结
运用双指针算法时不仅仅要找到某种性质(解题的关键——单调性),同时也别忘了指针i、j的范围已经更新问题!
参考学习:acwing算法基础课