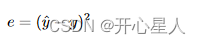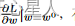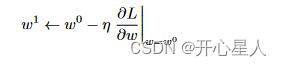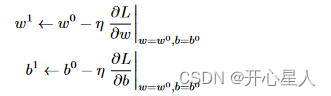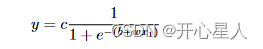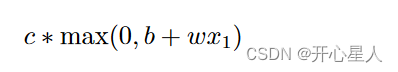机器学习就是让机器具备找一个函数的能力
带有未知的参数的函数称为模型
通常一个模型的修改,往往来自于对这个问题的理解,即领域知识。
损失函数
- 平均绝对误差(Mean Absolute Error,MAE)
- 均方误差(Mean Squared Error,MSE)
- 交叉熵(cross entropy):有一些任务中 y 和 ^y 都是概率分布,这个时候可能会选择交叉熵
梯度下降
解一个最优化的问题。把未知的参数找一个数值出来,看代哪一个数值进去可以让损失 L 的值最小。
梯度下降(gradient descent)是经常会使用优化的方法
假设只有一个未知参数w,怎么样找一个 w 让损失的值最小。
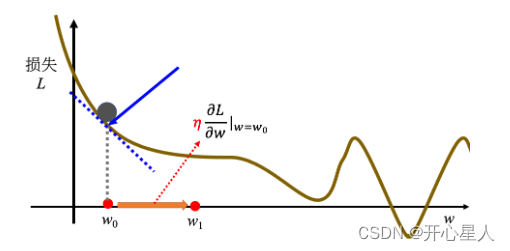
首先要随机选取一个初始的点 w0,计算在 w 等于 w0 的时候,参数 w 对损失L的微分
计算在这一个点,在 w0 这个位置的误差表面的切线斜率,也就是这一条蓝色的虚线,它的斜率,如果这一条虚线的斜率是负的,代表说左边比较高,右边比较低。在这个位置附近,左边比较高,右边比较低。如果左边比较高右边比较低的话,就把 w 的值变大,就可以让损失变小。如果算出来的斜率是正的,就代表左边比较低右边比较高。左边比较低右边比较高,如果左边比较低右边比较高的话,就代表把 w 变小了,w 往左边移,可以让损失的值变小
w左右移动的步伐大小取决于:
- 1、斜率,斜率大步伐就跨大一点,斜率小步伐就跨小一点
- 2、学习率(learning rate)η 也会影响步伐大小。学习率是自己设定的,如果 η 设大一点,每次参数更新就会量大,学习可能就比较快。如果 η 设小一点,参数更新就很慢,每次只会改变一点点参数的数值。(在做机器学习,需要自己设定,不是机器自己找出来的,称为超参数(hyperparameter))
所以w的更新如下:
不断地移动 w 的位置,最后会停下来。往往有两种情况会停下来
- 1、设定更新次数的超参数:上限可能会设为 100 万次,参数更新 100 万次后,就不再更新了
- 2、当不断调整参数,调整到一个地方,它的微分的值就是这一项,算出来正好是 0 的时候,如果这一项正好算出来是 0,0 乘上学习率 η 还是 0,所以参数就不会再移动位置
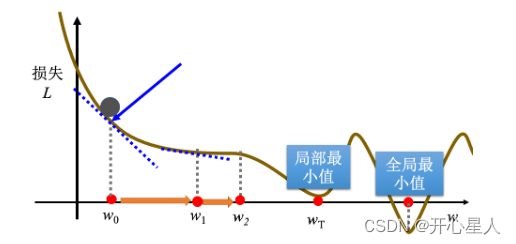
局部最小值和全局最小值问题
梯度下降有一个很大的问题,没有找到真正最好的解,没有找到可以让损失最小的 w。
如果在梯度下降中,w0 是随机初始的位置,也很有可能走到 wT 这里,训练就停住了,无法再移动 w 的位置。(事实上局部最小值是一个假问题,在做梯度下降的时候,真正面对的难题不是局部最小值。)
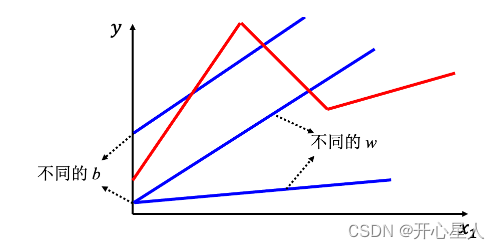
对于有多个未知参数,w、b。
激活函数
线性模型,不管如何设置 w 跟 b,永远制造不出红色线,永远无法用线性模型制造红色线。显然线性模型有很大的限制,这一种来自于模型的限制称为模型的偏差,无法模拟真实的情况。
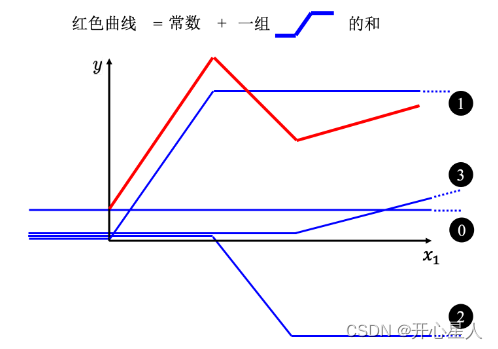
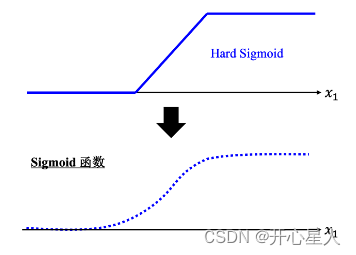
所以需要写一个更复杂的、更有灵活性的、有未知参数的函数。红色的曲线可以看作是一个常数再加上一群 Hard Sigmoid 函数。Hard Sigmoid 函数的特性是当输入的值,当 x 轴的值小于某一个阈值(某个定值)的时候,大于另外一个定值阈值的时候,中间有一个斜坡。所以它是先水平的,再斜坡,再水平的。所以红色的线可以看作是一个常数项加一大堆的蓝色函数(Hard Sigmoid)
假设 x 跟 y 的关系非常复杂也没关系,就想办法写一个带有未知数的函数。直接写 Hard Sigmoid 不是很容易,但是可以用一条曲线来理解它,用Sigmoid 函数来逼近 Hard Sigmoid,
Sigmoid 函数的表达式为
Hard Sigmoid 可以看作是两个修正线性单元(Rectified Linear Unit,ReLU)的加总
Sigmoid 和 ReLU 是最常见的激活函数
https://blog.csdn.net/caip12999203000/article/details/127067360
批量
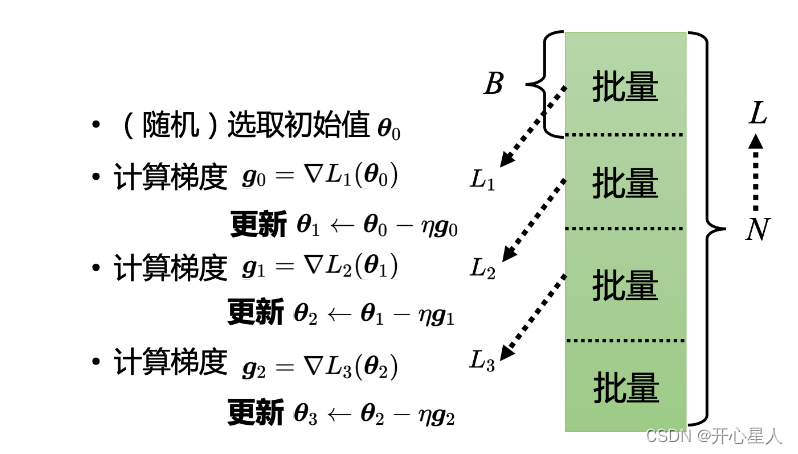
实际使用梯度下降的时候,会把 N 笔数据随机分成一个一个的批量(batch),一组一组的。每个批量里面有 B 笔数据,所以本来有 N笔数据,现在 B 笔数据一组,一组叫做批量
本来是把所有的数据拿出来算一个损失,现在只拿一个批量里面的数据出来算一个损失
所以实现上每次会先选一个批量,用该批量来算 L1,根据 L1 来算梯度,再用梯度来更新参数,接下来再选下一个批量算出 L2,根据 L2 算出梯度,再更新参数,再取下一个批量算出 L3,根据 L3 算出梯度,再用 L3 算出来的梯度来更新参数。
所以并不是拿 L 来算梯度,实际上是拿一个批量算出来的 L1, L2, L3 来计算梯度。把所有的批量都看过一次,称为一个回合(epoch),每一次更新参数叫做一次更新。
举个例子,假设有 10000 笔数据,即 N 等于 10000,批量的大小是设 10,也就 B 等于 10。10000 个样本(example)形成了 1000 个批量,所以在一个回合里面更新了参数 1000 次,所以一个回合并不是更新参数一次,在这个例子里面一个回合,已经更新了参数 1000 次了。
所以做了一个回合的训练其实不知道它更新了几次参数,有可能 1000 次,也有可能 10 次,取决于它的批量大小有多大。 批量大小是超参数
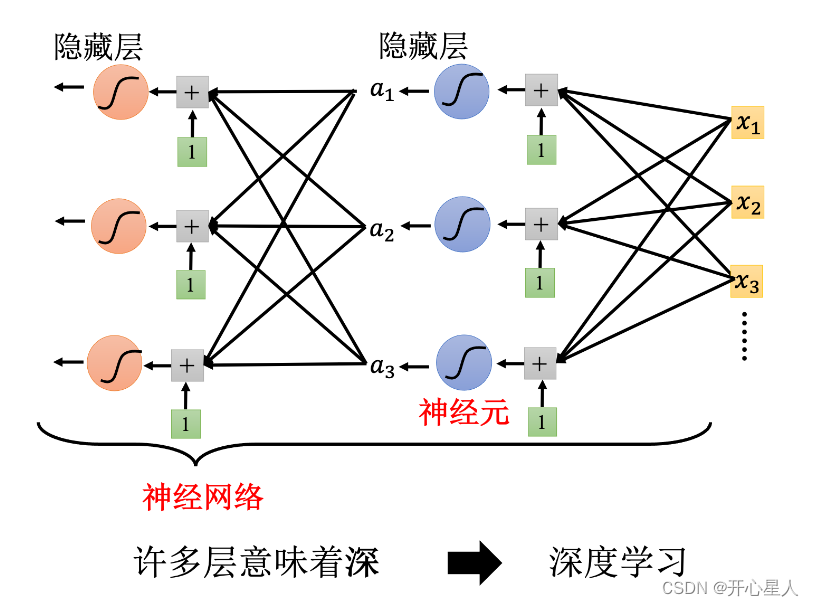
深度学习
Sigmoid 或 ReLU 称为神经元(neuron),很多的神经元称为神经网络(neural network)
每一排称为一层,称为隐藏层(hidden layer),很多的隐藏层就“深”,这套技术称为深度学习。
深度学习的训练会用到反向传播(BackPropagation,BP),其实它就是比较有效率、算梯度的方法。