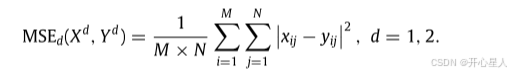摘要

motivation：PD计算过程非常耗时，严重限制了TDA的应用

本文提出了一种端到端的神经网络模型TopologyNet，用于直接从3D点云数据中拟合拓扑表示。TopologyNet显著减少了生成拓扑表示的计算时间，并在实际实例中保持了较小的近似误差。

TopologyNet被用于点云生成，作为点云自编码器的拓扑分支，以改善性能，并在潜在的生成对抗网络中使用额外的拓扑特征来产生新的点云(·提出了具有拓扑自动编码器的I-GAN模型，以提高新生成的点云的质量)。

引言

Achlioptas等人[3]探索了使用深度架构来学习表示，并引入了第一个点云的深度生成模型。特别地，提出了一种自动编码器，使用PointNet编码器将输入转换为隐藏向量。然而，大多数方法显式地考虑了数据的几何信息，而不是数据的拓扑结构。

在大规模数据集上高效地计算持久性同调（PDs）是一个具有挑战性的问题。例如，当基于Vietoris–Rips复形在包含5000个点的3D点云上计算1-PD时，需考虑$C_{5000}^2\approx 1.25\times 10^7$ 个1-单纯形和$C_{5000}^3\approx 2.08\times 10^{10}$个2-单纯形，随着半径参数增加到无限大。如果每个单纯形使用1 B的内存存储空间，则需要约19.4 GB的内存来存储这些单纯形。此外，持久性同调算法的时间复杂度与单纯形数量成正比。持久性同调的经典算法在实际实例上的复杂度接近线性，而在最坏情况下的复杂度为三次方。一台普通计算机在这种情况下计算1-PD将需要很长时间，甚至可能导致内存溢出。因此，特别是在深度学习场景中，需要一种高效的方法来估算持久性同调（PDs）。

相关工作

点云的几何神经网络: 为了处理不规则点，PointNet 使用多层感知器（MLP）提取点特征，并使用最大池化来获得最终的特征。PointNet++ 设计了一个分层框架，该框架在输入点云集的嵌套划分上递归地应用PointNet，以利用具有递增感受野的局部上下文。其他方法则提出了不同的点卷积算子，以提高特征提取的效果。Wang等人 [12] 提出了一个动态图卷积神经网络，他们开发了EdgeConv模块以有效地提取局部上下文。除了EdgeConv之外，其他卷积方法还包括SplineConv [22] 和GraphConv [23]。对于点云生成，Achlioptas等人 [3] 提出了一个自动编码器来学习与输入对应的隐藏向量。然而，这些卷积方法都没有直接考虑数据的拓扑结构。

持久同源性和深度学习：持久同源性可以是神经网络的另一个分支。一些研究已经使用显式拓扑先验和拓扑损失函数进行图像分割[24-26]。Brüel-Gabrielsson等人[27]提出了一种可微拓扑层，采用持久性设计可微损失，基于水平集过滤和基于边的过滤计算PD，然后将PD点映射回分别创建和破坏同调类的单形，通过梯度下降更新与这些单形顶点相关的坐标或参数。该拓扑层通过在深度生成网络的输出上构造包含拓扑先验的拓扑损失来提高生成的点云和体素的拓扑质量。然而，该方法依赖于传统的持久同源性计算方法，并且当过滤变得过大时可能遭受低效的计算。此外，PD被学习为图像分类任务中的特征。霍费尔等人[28]提出了一种用于拓扑签名的网络层，以分类2D图像。然而，他们没有将持久同源性扩展到3D点云场。

PI：(1)该表示是向量;（2）该表示可以反映持久特征并保留PD中包含的信息（3）该表示相对于噪声是稳定的。

EdgeConv是一种用于处理点云数据的图卷积网络（GCN）模块。它由Wang等人在2019年提出，并在论文《Dynamic Graph CNN for Learning on Point Clouds》中进行了详细描述。EdgeConv的核心思想是动态地构建图结构，并在这个图上应用卷积操作来提取点云的局部特征。通过动态图构建和边特征提取，EdgeConv能够捕捉点云数据的局部几何结构

1. 动态图构建：

   • 在传统的图卷积网络中，图结构通常是预先定义好的，不会随着输入数据的变化而变化。而EdgeConv能够根据每个输入点云动态地构建图结构。
   • 对于每个输入点，EdgeConv会搜索其$k$个最近邻点，构建从一个点到另一个点的有向边，形成一个有向图。这个过程中还会为每个点添加自环（self-loop），以包含点自身的信息。

2. 边特征提取：

   • EdgeConv通过一个可学习的函数 $h_{\theta }$ 来计算每条边的特征。这个函数通常是一个具有参数 $\theta$ 的神经网络，它可以从两个顶点的特征中学习边的特征表示。
   • 对于图中的每条边 $(x_{l_1},x_{l_2})$，EdgeConv计算边特征 $e_{1,2}=h_{\theta }(x_{l_1},x_{l_2})$。

3. 特征聚合：

   • 利用对称的聚合函数（如最大池化）来聚合与每个顶点相关的所有边的特征。这样，每个顶点的新特征表示为与该顶点相关的所有边特征的聚合结果。
   • 公式表示为： x i ′ = □ l ∈ { i , ( j , 1 ) , . . . , ( j , k ) } h θ ( x i , x ) x'_i = \square_{l \in \{i, (j,1), ..., (j,k)\}} h_\theta(x_i, x) xi′​=□l∈{i,(j,1),...,(j,k)}​hθ​(xi​,x)，其中 $x_i^{\prime }$ 是第 $i$ 个顶点的输出特征，$\square$ 是聚合函数。

4. 多尺度特征融合：

   • EdgeConv通常堆叠多个层，每层可以捕捉不同尺度的局部特征。通过这种方式，网络能够学习到点云的多尺度表示。

5. 适用于不规则数据：

   • 由于点云数据通常是无序的且分布不均匀，EdgeConv能够很好地处理这种不规则性，因为它在局部邻域内构建图结构，而不是依赖于全局的规则网格结构。

TopologyNet

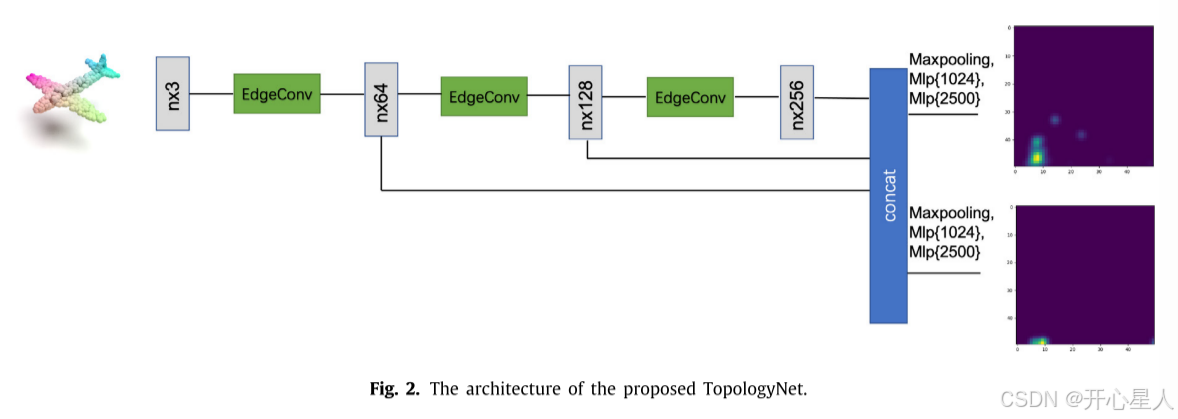
TopologyNet可以学习3D点云及其相应PI之间的映射

在该架构中，三个堆叠的EdgeConv模块被用作点云卷积算子。然后，将来自三个EdgeConv层的特征向量连接以获得多尺度特征。并行地，采用最大池化和两个MLP通过共享通过EdgeConv层提取的特征来分别产生预测的1-PI和2-PI。

用于预测1-PI和2-PI的网络的EdgeConv层中的相应参数之间的差异很小，并且不同维度PI的预测主要受MLP层的影响。因此，在训练阶段采用多任务学习策略，对EdgeConv层模块中的参数进行共享和联合优化，提高了TopologyNet的训练效率。

此外，点云的PI（点集不变性）对点的顺序是不变的。因此，采用了对称聚合函数最大池化（max pooling）来合并特征，这避免了由于点云中点的不同排序而产生的影响。

此外，PD和PI是旋转和平移不变的。因此，对样本进行归一化的技巧可以消除平移对生成PI的影响，而样本增强则通过在训练阶段随机旋转每批数据，使训练好的网络尽可能生成旋转不变的PI。

此外，通过使用子采样技术（如最远点采样）和超采样技术（如简单点复制），将具有不固定数量点的输入点云采样为1024 × 3，固定数量的点作为所提出的网络的输入。

可微拓扑损失


λ是一个权重超参数

TopologyNet是一个端到端的工具，用于预测3D点云的拓扑特征，同时用可微神经网络代替不可微的计算。因此，在上面的loss关注输入点云的拓扑结构，即环和洞，可作为本工作中点云生成相关任务的正则化损失项。

拓扑自动编码器

拓扑分支，不需要将其作为正则化损失项来约束点云的生成，而是能够有效地提取由PI表示的拓扑特征。

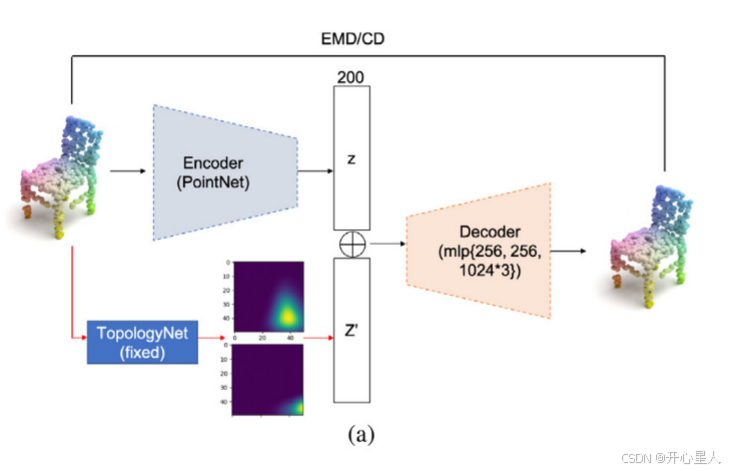
在ModelNet 40上训练TopologyNet后，我们固定了TopologyNet的参数，并将其视为拓扑特征提取算子。除了拓扑分支之外，第二个编码器分支是具有最大池化聚合函数的公共PointNet编码器。

编码器在原始1024 × 3点集输入上运行。它由五个1 × 1卷积和批归一化层组成，分别具有64、128、128、256和200个通道。最大池化层聚合所有点的特征，并输出具有200个维度的隐藏向量z。
拓扑分支使用TopologyNet提取50 × 50的1-PI和2-PI。为了减少原始PI的维数，我们使用了平均池操作。具体来说，使用的核大小为5 × 5，步长为5个像素。因此，得到两个10 × 10的1-PI和2-PI作为输出，这是两个100维向量。最后，将这两个矢量连接起来，得到一个200维拓扑特征矢量z′，表示输入点云的环和二维孔洞。
我们使用元素加法函数来合并两个隐藏向量z和z′。我们的解码器包括3个MLP层，分别为256，256和1024 × 3单元，可以生成大小为1024 × 3的点云。

误差评估：
1、与baseline自动编码器进行比较，使用CD或EMD定量测量
2、比较输入和输出点云差异，通过比较点云对应PD的差异性，使用1-WD

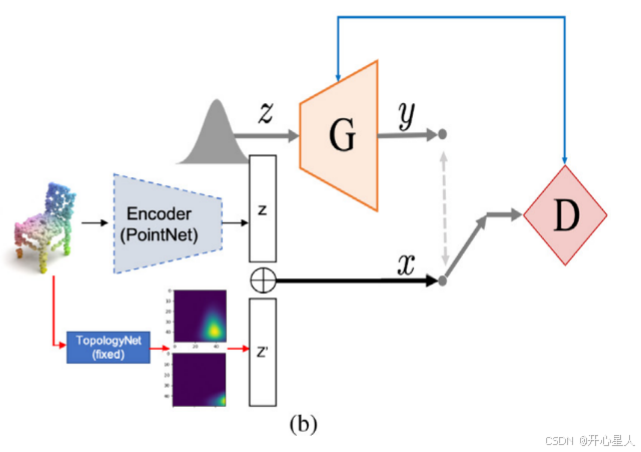
具有拓扑自动编码器的GAN

生成器输入从高斯分布采样的随机变量以预测潜在变量作为输出。
在对抗训练中，利用拓扑自动编码器产生的潜在变量对鉴别器进行训练，使生成器的输出更接近潜在变量。
最后，将训练好的生成器的输出输入到拓扑自动编码器的解码器中，以生成新的点云。

G是生成器，D表示鉴别器。隐藏向量的长度设为200。具体地说，生成器由两个完全连接的层组成，它们的尺寸分别为128 × 128和128 × 200，ReLU作为它们的激活函数。鉴别器由三个完全相连的层组成，它们的大小分别为200 × 256、256 × 512和512 × 1;前两层使用ReLU作为它们的激活函数，而最后一层使用sigmoid。

在对抗训练中，使用带有梯度惩罚的Wasserstein GAN 的损失函数来训练网络。该方法采用梯度罚函数法解决了网络训练困难和不收敛的问题。通过增加真实的样本区域、生成样本区域和插值样本区域的梯度约束，可以避免训练鉴别器时梯度过大的问题。