Bootstrap

3 ＞ 数据结构与算法 栈与队列

概览

本节总结了栈和队列的基本概念和用法，另外附上栈与队列的基本操作代码（C语言版）。
本节适合有C语言基础的初学者、期末复习、考研等方面的用途。

栈

  1. 只允许在一端插入和删除操作的线性表。代码如下
  2. 特点：先进后出模式（LIFO），只能在栈顶操作。
  3. 什么是卡特兰数：有 n 个元素进栈（顺序可以不同），出栈元素不同的排列个数为 1 n + 1 C 2 n n \frac{1}{n+1}C^n_{2n} n+11​C2nn​。
  4. 共享栈：两个栈共享同一片存储空间，两个栈分别从存储空间的两端逐渐向中间增长，当两个栈的栈顶相遇时，则栈满。（此方式可以降低栈上溢的可能）
  5. 理想情况下，入栈、出栈的时间复杂度： O ( 1 ) O(1) O(1)
数组栈
#include "stdio.h"
#include "malloc.h"
#include "stdbool.h"
#define SElemType int
#define STACK_INIT_SIZE 10 //栈初始大小
#define STACK_INCREMENT 2 //栈递增大小
typedef struct SqStack {
    SElemType *base; //在栈构造之前和销毁之后，base的值为NULL
    SElemType *top; //栈顶指针
    int stacksize; //当前已分配的存储空间，以元素为单位
}SqStack;
void InitStack(SqStack *S) {  //构造一个空栈S
    (*S).base=(SElemType *)malloc(STACK_INIT_SIZE*sizeof(SElemType));
    if(!(*S).base)
        exit(1);
    (*S).top=(*S).base;
    (*S).stacksize=STACK_INIT_SIZE;
}
void DestroyStack(SqStack *S) {	//销毁栈S，S不再存在
    free((*S).base);
    (*S).base=NULL;
    (*S).top=NULL;
    (*S).stacksize=0;
}
bool StackEmpty(SqStack S) {	//若栈S为空栈，则返回TRUE，否则返回FALSE
    if(S.top==S.base)
        return true;
    else
        return false;
}
int StackLength(SqStack S) {	//返回S的元素个数，即栈的长度
    return S.top-S.base;
}
bool GetTop(SqStack S,SElemType *e) { //若栈不空，则用e返回S的栈顶元素，并返回TRUE；否则返回FALSE
    if(S.top>S.base) {
        *e=*(S.top-1);
        return true;
    }
    else
        return false;
}
void Push(SqStack *S,SElemType e) {	//插入元素e为新的栈顶元素
    if((*S).top-(*S).base>=(*S).stacksize) {
        (*S).base=(SElemType *)realloc((*S).base,((*S).stacksize+STACK_INCREMENT)*sizeof(SElemType));
        if(!(*S).base)
            exit(1);
        (*S).top=(*S).base+(*S).stacksize;
        (*S).stacksize+=STACK_INCREMENT;
    }
    *((*S).top)++=e;
}
bool Pop(SqStack *S,SElemType *e) { //若栈不空，则弹出S的栈顶元素，用e返回其值，并返回TRUE；否则返回FALSE
    if((*S).top==(*S).base)
        return false;
    *e=*--(*S).top;
    return true;
}
void StackTraverse(SqStack S,void(*visit)(SElemType)) {	//从栈底到栈顶依次对栈中每个元素调用函数visit()
    while(S.top>S.base)
        visit(*S.base++);
    printf("\n");
}
void PrintElement(SElemType e) {  //visit函数
    printf("%d ", e);
}
int main() {
    //创建顺序栈并初始化
    SqStack stack;
    InitStack(&stack);
    // 插入一些元素
    Push(&stack, 1);
    Push(&stack, 2);
    Push(&stack, 3);
    printf("Stack Length: %d\n", StackLength(stack));
    // 依次打印这些元素
    printf("Stack Elements: ");
    StackTraverse(stack, PrintElement);
    // 从栈顶依次取出元素
    SElemType popped_element;
    while (Pop(&stack, &popped_element)) {
        printf("Popped Element: %d\n", popped_element);
    }
    printf("Stack Length: %d\n", StackLength(stack));
    //销毁顺序栈
    DestroyStack(&stack);

    return 0;
}
链栈
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ElemType int
typedef struct Node { // 定义链表结点
    ElemType data;
    struct Node *next;
} Node;
typedef struct { // 定义链表栈结构
    Node *top; // 栈顶指针
} LinkStack;
void InitStack(LinkStack *stack) { // 初始化链表栈
    stack->top = NULL;
}
void DestroyStack(LinkStack *stack) { // 销毁链表栈
    Node *p = stack->top;
    while (p) {
        Node *temp = p;
        p = p->next;
        free(temp);
    }
    stack->top = NULL;
}
bool StackEmpty(LinkStack stack) { // 判断栈是否为空
    return stack.top == NULL;
}
bool GetTop(LinkStack stack, ElemType *e) { // 获取栈顶元素
    if (StackEmpty(stack)) {
        return false; // 栈为空，无法获取栈顶元素
    }
    *e = stack.top->data;
    return true;
}
bool Push(LinkStack *stack, ElemType e) { // 入栈操作
    Node *newNode = (Node *)malloc(sizeof(Node));
    if (!newNode) {
        printf("内存分配失败");
        return false;
    }
    newNode->data = e;
    newNode->next = stack->top;
    stack->top = newNode;
    return true;
}
bool Pop(LinkStack *stack, ElemType *e) { // 出栈操作
    if (StackEmpty(*stack)) {
        printf("空栈");
        return false;
    }
    Node *temp = stack->top;
    *e = temp->data;
    stack->top = temp->next;
    free(temp);
    return true;
}
void ClearStack(LinkStack *stack) { // 清空栈
    Node *p = stack->top;
    while (p) {
        Node *temp = p;
        p = p->next;
        free(temp);
    }
    stack->top = NULL;
}
int StackLength(LinkStack stack) { // 链表栈的长度
    int length = 0;
    Node *p = stack.top;
    while (p) {
        length++;
        p = p->next;
    }
    return length;
}
bool GetElement(LinkStack stack, int index, ElemType *e) { // 根据索引获取栈中元素
    if (index < 1 || index > StackLength(stack)) {
        printf("非法索引值");
        return false;
    }
    Node *p = stack.top;
    for (int i = 1; i < index; i++) {
        p = p->next;
    }
    *e = p->data;
    return true;
}
bool ModifyElement(LinkStack *stack, int index, ElemType e) { // 修改栈中指定索引的元素
    if (index < 1 || index > StackLength(*stack)) {
        printf("非法索引值");
        return false;
    }
    Node *p = stack->top;
    for (int i = 1; i < index; i++) {
        p = p->next;
    }
    p->data = e;
    return true;
}
bool DeleteElement(LinkStack *stack, int index, ElemType *e) { // 删除栈中指定索引的元素
    if (index < 1 || index > StackLength(*stack)) {
        printf("非法索引值");
        return false;
    }
    Node *p = stack->top;
    if (index == 1) {
        stack->top = p->next;
    } else {
        Node *pre = NULL;
        for (int i = 1; i < index; i++) {
            pre = p;
            p = p->next;
        }
        pre->next = p->next;
    }
    *e = p->data;
    free(p);
    return true;
}
void PrintStack(LinkStack stack) { // 打印栈中元素
    Node *p = stack.top;
    printf("Stack Elements: ");
    while (p) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}
int main() {
    //初始化堆栈
    LinkStack stack;
    InitStack(&stack);
    //向堆栈中存入数据
    Push(&stack, 1);
    Push(&stack, 2);
    Push(&stack, 3);
    printf("Stack Length: %d\n", StackLength(stack));
    //打印堆栈
    PrintStack(stack);
    //获取栈顶数据
    ElemType top_element;
    if (GetTop(stack, &top_element)) {
        printf("Top Element: %d\n", top_element);
    }
    //取出栈顶数据
    ElemType popped_element;
    if (Pop(&stack, &popped_element)) {
        printf("Popped Element: %d\n", popped_element);
    }
    printf("Stack Length after popping: %d\n", StackLength(stack));
    //调整堆栈的2号数据为5
    ModifyElement(&stack, 2, 5);
    PrintStack(stack);
    //销毁堆栈
    DestroyStack(&stack);

    return 0;
}

队列

  1. 只允许一端进（队尾），另一端出（队头）。
  2. 特点：先进先出模式（FIFO），根据不同类型的队列有不同的入队和出队方式。
  3. 理想情况下，入队、出队的时间复杂度： O ( 1 ) O(1) O(1)
  4. 顺序队列：（一般采用环状队列）代码如下
    1. 用取模运算将存储空间在逻辑上变成环状。
    2. 元素个数计算：
      1. 设置 “len” 存储数据个数；（不牺牲任何存储单元）
      2. ( r e a r − f r o n t + M + 1 )   %   M (rear-front+M+1)~\%~M (rear−front+M+1) % M（rear指针指向队尾元素）
      3. ( r e a r − f r o n t + M )   %   M (rear-front+M)~\%~M (rear−front+M) % M（必须牺牲一个存储单元，rear 指针指向队尾元素下一位）
    3. 判满和判空方法：
      1. 牺牲一个存储单元，防止两指针指向同一位置出现判空判满为相同条件，
      2. 设置变量实时存储队列长度，
      3. 设置标记 tag，数据入队 tag=0，数据出队 tag=1；当最后一次 tag=0 且两个指针指向相同位置则满。当 tag=1 且两个指针指向相同位置则为空。
  5. 链表队列
  6. 双端队列：
    1. 全功能队列：两端都可以输入和输出
    2. 输入受限：只允许其中一端输入、但两端都可以输出
    3. 输出受限：两端都可以输入，但只允许其中一端输出
    4. 栈属于阉割版的双端队列
环状顺序队列
#include <stdio.h>
#include <stdbool.h>
#define MAX_SIZE 10 // 队列最大容量为10

typedef int ElemType;
typedef struct {
    ElemType data[MAX_SIZE];
    int front; // 队头指针
    int rear;  // 队尾指针
} CircularQueue;
// 初始化环状顺序队列
void InitQueue(CircularQueue *queue) {
    queue->front = 0;
    queue->rear = 0;
}
// 销毁环状顺序队列
void DestroyQueue(CircularQueue *queue) {
    queue->front = 0;
    queue->rear = 0;
}
// 判断队列是否为空
bool QueueEmpty(CircularQueue queue) {
    return queue.front == queue.rear;  //牺牲一个存储单元作为判空和判满的条件
}
// 判断队列是否已满
bool QueueFull(CircularQueue queue) {
    return (queue.rear + 1) % MAX_SIZE == queue.front;
}
// 入队操作
bool EnQueue(CircularQueue *queue, ElemType e) {
    if (QueueFull(*queue)) {
        return false; // 队列已满，无法入队
    }
    queue->data[queue->rear] = e;
    queue->rear = (queue->rear + 1) % MAX_SIZE; // 队尾指针后移
    return true;
}
// 出队操作
bool DeQueue(CircularQueue *queue, ElemType *e) {
    if (QueueEmpty(*queue)) {
        return false; // 队列为空，无法出队
    }
    *e = queue->data[queue->front];
    queue->front = (queue->front + 1) % MAX_SIZE; // 队头指针后移
    return true;
}
// 获取队头元素
bool GetFront(CircularQueue queue, ElemType *e) {
    if (QueueEmpty(queue)) {
        return false; // 队列为空，无法获取队头元素
    }
    *e = queue.data[queue.front];
    return true;
}
// 获取队尾元素
bool GetRear(CircularQueue queue, ElemType *e) {
    if (QueueEmpty(queue)) {
        return false; // 队列为空，无法获取队尾元素
    }
    *e = queue.data[(queue.rear - 1 + MAX_SIZE) % MAX_SIZE];
    return true;
}
int main() {
    //创建并初始化队列
    CircularQueue queue;
    InitQueue(&queue);
    //添加元素
    EnQueue(&queue, 1);
    EnQueue(&queue, 2);
    EnQueue(&queue, 3);
    //获取队头元素
    ElemType front_element, rear_element;
    if (GetFront(queue, &front_element)) {
        printf("Front Element: %d\n", front_element);
    }
    //获取队尾元素
    if (GetRear(queue, &rear_element)) {
        printf("Rear Element: %d\n", rear_element);
    }
    //出队操作
    ElemType dequeued_element;
    while (DeQueue(&queue, &dequeued_element)) {
        printf("Dequeued Element: %d\n", dequeued_element);
    }
    //销毁队列
    DestroyQueue(&queue);

    return 0;
}

应用

  1. 括号匹配：（栈的应用）代码如下
    1. 依次扫描括号，遇到左括号进栈，遇到右括号出栈一个栈内元素，比较出栈元素和当前右括号是否相同，不同则失败；
    2. 匹配完后栈内还有元素则说明还有左括号未匹配，匹配失败；
    3. 匹配未完时遇到右括号而栈为空，则没有与之匹配的左括号，匹配失败。
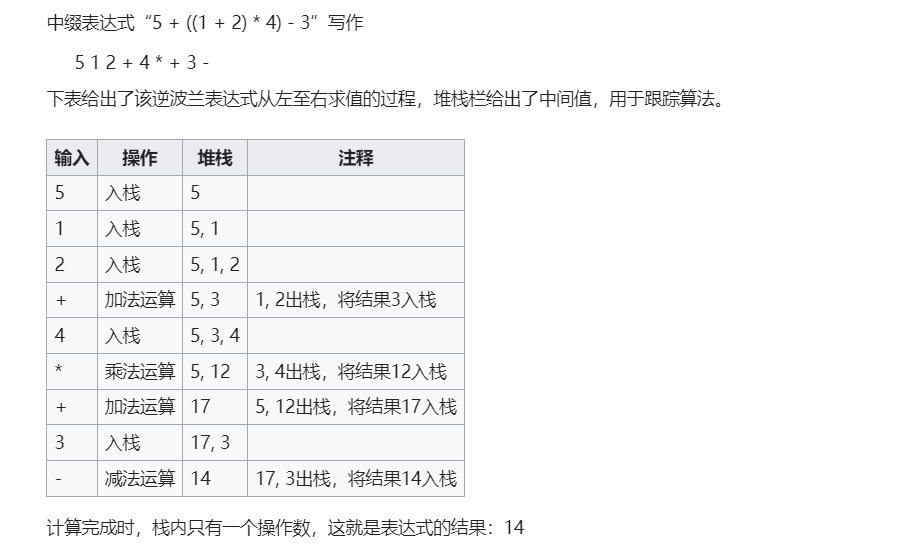
  2. 表达式计算：（栈的应用）
    1. 波兰表达式（又称前缀表达式）
    2. 逆波兰表达式（又称后缀表达式）（在机算和手算要确保 ”左优先“ 原则）
      来自维基百科的逆波兰式示例
    3. 后缀表达式求值：
      1. 依次扫描每个元素，直到扫描完所有元素，
      2. 遇见数字直接入栈，
      3. 遇见符号从栈中取出两个元素，执行运算，将运算后的元素入栈。
  3. 局部变量的存储采用栈进行；
  4. 函数套娃式调用特点：最里面函数的最先执行
    1. 递归能做什么：把原始问题转换成属性相同，但规模较小的问题。
    2. 递归调用时，函数调用栈可称为“递归工作栈”：
      1. 每递归一次，就将递归调用所需的数据加入栈顶，
      2. 每解递归一次，就会将栈顶的计算数据弹出栈顶，并将数据传入下一递归层。
    3. 效率低下，可能包含很多重复运算；递归调用过多将导致栈溢出。
    4. 递归调用越多，则空间复杂度越高。
    5. 与递归算法求解问题相比，通常非递归算法更高效。
  5. 队列的应用：
    1. 树的层次遍历
    2. 图的广度优先遍历
    3. 多个进程争抢有限系统资源的先来先服务策略（FCFS）
    4. 缓冲区
  6. 矩阵的压缩存储：
    1. 行优先存储：一行一行的存。
    2. 列优先存储：一列一列的存。
    3. 对称矩阵：（数组下标统一从 0 开始）
      1. 只存储主对角线+上（下）三角区数据，一维数组大小为 ( 1 + n ) n 2 \frac{(1+n)n}{2} 2(1+n)n​。
      2. 按照行优先：要访问第 i 行 j 列的元素，则第 i − 1 i-1 i−1 行有 i ∗ ( i − 1 ) / 2 i*(i-1)/2 i∗(i−1)/2 个元素，第 i 列有 j 个元素，一维数组表为 ( i ∗ ( i − 1 ) ) / 2 + j − 1 (i*(i-1))/2+j-1 (i∗(i−1))/2+j−1。（从数据少的行列向数据多的行列访问）
      3. 按照列优先：要访问第 i 行 j 列的元素，则 j − 1 j-1 j−1 列总共有 n − ( ( j − 1 ) − 1 ) n-((j-1)-1) n−((j−1)−1) 个元素，第 j 列有 i − j i-j i−j个元素，则数据位置为 − [ n + ( n − j + 2 ) ] / 2 + i − j + 1 − 1 -[n+(n-j+2)]/2+i-j+1-1 −[n+(n−j+2)]/2+i−j+1−1号。（从数据多的行列向数据少的行列访问）
    4. 三角矩阵：
      1. 上（下）三角区域不是（是）常量，除开对角线。
      2. 按行列优先访问方式和对称矩阵一样。
    5. 三对角矩阵：（带状矩阵）
      1. 当 |i-j|>1时，元素就为0。
      2. 行优先时：一维 数组位置为 k=(3*(i-1)-1)+(j-i+2)-1 号,列优先调换 i j 一样的。
      3. 通过一维数组（位置为 k）确定二维数组位置：3*(i-1)-1<k+1≤3*i-1，k向上取整。
    6. 稀疏矩阵的压缩存储：
      1. 采用顺序存储：用三元组，存储非零元素的行、列和值。
      2. 采用链式存储：
        • 定义直角坐标形式的两个数组（数组每个元素为指针，分别向下向右指向非零元素位置），
        • 每个元素节点包含行（列）位置、数据、指向同行（列）下一元素指针。
      3. 稀疏矩阵的随机存储特性：
        • 无法直接访问元素：不能和普通数组一样通过行列访问；
        • 修改和插入元素困难：修改原矩阵后，可能需要重新组织存储结构；
        • 逻辑关系和运算更加复杂。
括号匹配
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>
typedef struct { // 定义栈结构
    char *data; // 栈数组指针
    int top;    // 栈顶指针
    int maxSize; // 栈最大容量
} Stack;
void initStack(Stack *stack, int maxSize) { // 初始化栈
    stack->data = (char *)malloc(maxSize * sizeof(char));
    stack->top = -1;
    stack->maxSize = maxSize;
}
void destroyStack(Stack *stack) { // 销毁栈
    free(stack->data);
    stack->data = NULL;
    stack->top = -1;
    stack->maxSize = 0;
}
bool isEmpty(Stack *stack) { // 判断栈是否为空
    return stack->top == -1;
}
bool push(Stack *stack, char c) { // 入栈
    if (stack->top == stack->maxSize - 1) {
        return false; // 栈满，无法入栈
    }
    stack->data[++stack->top] = c;
    return true;
} 
bool pop(Stack *stack, char *c) { // 出栈
    if (isEmpty(stack)) {
        return false; // 栈空，无法出栈
    }
    *c = stack->data[stack->top--];
    return true;
}
bool isValid(char *s) { // 括号匹配函数
    Stack stack;
    initStack(&stack, strlen(s)); // 初始化栈
    int i = 0;
    while (s[i] != '\0') {
        if (s[i] == '(' || s[i] == '[' || s[i] == '{') {
            push(&stack, s[i]); // 左括号入栈
        } else if (s[i] == ')' || s[i] == ']' || s[i] == '}') {
            char top;
            if (pop(&stack, &top)) {
                // 检查右括号是否匹配栈顶的左括号
                if ((s[i] == ')' && top != '(') ||
                    (s[i] == ']' && top != '[') ||
                    (s[i] == '}' && top != '{')) {
                    destroyStack(&stack);
                    return false; // 括号不匹配
                }
            } else {
                destroyStack(&stack);
                return false; // 栈空，没有左括号与之匹配
            }
        }
        i++;
    }
    bool result = isEmpty(&stack); // 判断栈是否为空
    destroyStack(&stack); // 销毁栈
    return result;
}
int main() {
    char expr1[] = "{[()]}";
    char expr2[] = "{[()]}[";
    printf("表达式 1 : %s\n", isValid(expr1) ? "正确" : "错误");
    printf("表达式 2 : %s\n", isValid(expr2) ? "正确" : "错误");
    return 0;
}

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
大数据知识面试题-Flume（2022版）
React的生命周期？
《Python进阶系列》二十八：mmap模块（处理大文本）
vue实现pc和移动端布局
Watchdog driver API
kali linux多版本java共存并自由切换 update-alternatives
springboot+flowable 使用方式
打造智能家居：用React、Node.js和WebSocket构建ESP32设备控制面板（代码说明）
python文件处理-excel格式处理
[Android/Icon] 分享一个图标/Icon制作网站
;