复盘
7:40 开题
看 T1 发现又是数数?约束似乎比较多,T2 看起来比较可做,T3 应该是什么神奇计数dp,T4 一眼不太可做
推 T1,想到 “区间加” 这种操作其实很难在线性 dp 里维护,很多后效性,很快想到了在差分数组上拆成 +1 -1 的操作,然后 dp 状态里记录前缀 ,以为会了,直接开写了
发现样例没过,仔细手玩后发现题没看清,操作是有先后顺序的,(1,2)(2,2) 与 (2,2)(1,2) 不是同种方案!以为补个阶乘就行了,发现这样会多算,因为 (2,2)(2,2) 还是只有一种
然后就懵逼了,感觉左右端点拆开做的话就没法维护它们不同,笃定差分假了
然后又胡了个神奇钦定+容斥的做法,再次 十分自信 开写,写完一推样例发现假了… 呃呃呃
然后还在思考 T1,到剩下 2h 多的时候发现情况不对,先打暴力吧,十分慌
开 T2 ,一眼想到差分后找一段不互质的数,想想觉得是什么调和级数神奇值域做法,推了推发现避免不开对 O ( 1 e 18 ) O(1e18) O(1e18) 的数进行质因子分解,难蚌
冷静了一下发现按 r r r 往右扫,维护前面一段段 gcd 变化的位置即可,想想了这个做法复杂度最大 n l o g 2 V nlog^2V nlog2V,但 g c d gcd gcd 衰减的速度肯定比 l o g log log 快很多,开写
测大样例发现 910ms ,很极限;又打打表发现上面说的 g c d gcd gcd 变化的段通常都是 5 5 5 左右,觉得应该能很快。但还是决定和个超级快读,结果发现跑的更慢,于是换回一般快读
剩 50min,慌,看 T3 ,发现朴素的式子很好出,决定先打暴力吧
看 T4 ,发现暴力送了 55pts?但应该只打的完 35,写完后回去看 T1 ,拿点暴力
然后就 30pts 进厂了
so,30+70+15+30=145? rk_inf
( ps: T2 后面的 30pts 均只差了 100ms 以内,甚至那发超级快读获得了 85pts 的好成绩
节奏很崩的一场,发现自己很容易被 T1 搞心态,其实第一步差分的想法很接近正解了,但就是顺序问题一时没想清就把这个思路全盘否定了,而且还影响后面心态
另外就是想到做法一定要先手玩样例,最容易浪费时间的地方就是 调细节多的假做法…
还有就是应该先通览题面的,T3 这种我应该比较擅长的推式子最后也被迫放弃
所以以后的策略应该是:通览题面;不急着写代码,码之前一定要谨慎、理清思路;留足时间打暴力,不要看不起暴力
题解
T1
正解的模型转化更好,将区间左右端点 +1,-1 看作 括号匹配,这样更方便刻画匹配的方案数
设 f i , j , k f_{i,j,k} fi,j,k 表示 前 i i i 个位置,当前前缀和为 j j j , + 1 +1 +1 操作总共用了 k k k 次
从 i i i 转移到 i + 1 i+1 i+1 时,假设用 o o o 次 − 1 -1 −1 操作,要与前面的 j j j 匹配,由于这 o o o 个右括号都是一样的,但挑出来的 j j j 个左括号不一定,所以乘上 C j o × o ! C_j^o\times o! Cjo×o!;另外还有新匹配好的这 o o o 对插到长度为 k − j k-j k−j 的已完成的操作序列中,即:
f i , j , k × C j o × o ! × C k − j + o o → f i + 1 , j − o , k , 0 ≤ o ≤ j f_{i,j,k}\times C_j^o\times o!\times C_{k-j+o}^o\to f_{i+1,j-o,k}\ ,\ 0\leq o\leq j fi,j,k×Cjo×o!×Ck−j+oo→fi+1,j−o,k , 0≤o≤j
但这样会有个问题,我们相当于是认为了 这 j j j 个待匹配的左括号互不相同,实际上不是(赛时正是卡到这)
先说一种我赛后订题的想法:
担心若干的左括号会影响?我们直接 在加入左括号时提前 除以
p
!
p!
p! ,
p
p
p 代表左括号个数,强制认为它们不同,额,费用提前计算?
f i , j , k × C j o × o ! × C k − j + o o × 1 p ! → f i + 1 , j − o + p , k + p , 0 ≤ o ≤ j , 0 ≤ p ≤ m − k f_{i,j,k}\times C_j^o\times o!\times C_{k-j+o}^o\times \frac{1}{p!}\to f_{i+1,j-o+p,k+p}\ ,\ 0\leq o\leq j,0\leq p\leq m-k fi,j,k×Cjo×o!×Ck−j+oo×p!1→fi+1,j−o+p,k+p , 0≤o≤j,0≤p≤m−k
这样可以获得 65pts 的好成绩(听说实现好有85)
换一种更好的想法:
既然认为 操作有序 ,我们想象成 长度为 m m m 的一个操作序列,初始为空,每次往里面某些位置插入操作,需要考虑顺序
+1 操作看成往里面为空的位置放数,-1 操作看成往现有的未匹配的 +1 里放,匹配上
那么转移就变得简单:
f i , j , k × C j o × C m − k p → f i + 1 , j − o + p , k + p , 0 ≤ o ≤ j , 0 ≤ p ≤ m − k f_{i,j,k}\times C_j^o\times C_{m-k}^p\to f_{i+1,j-o+p,k+p}\ ,\ 0\leq o\leq j,0\leq p\leq m-k fi,j,k×Cjo×Cm−kp→fi+1,j−o+p,k+p , 0≤o≤j,0≤p≤m−k
复杂度 O ( n m 4 ) O(nm^4) O(nm4)
接下来的优化,我们考虑一个事情:这两种转移实际上是独立的
先增加多少 + 1 +1 +1 并不会影响 − 1 -1 −1 究竟可以与前面多少个 + 1 +1 +1 匹配,也就是说 j j j 与 p p p 的枚举是独立的
那么我们用两个数组:
f 0 f_0 f0 表示 i i i 位置已进行过两种转移,接下来在 i + 1 i+1 i+1 位置进行 + 1 +1 +1 操作
f 1 f_1 f1 表示 i i i 位置进行了 + 1 +1 +1 ,接下来要进行 − 1 -1 −1 转移
两步拆开枚举就能优化到 O ( n m 3 ) O(nm^3) O(nm3),又因为这个 m 3 m^3 m3 实际上是 C m 3 C_m^3 Cm3,常数极小,2.5s 可以通过
#include<bits/stdc++.h>
using namespace std ;
typedef long long LL ;
const int N = 105 , M = 305 ;
const int mod = 998244353 ;
LL ksm( LL a , LL b )
{
LL res = 1 , t = a % mod ;
while( b ) {
if( b&1 ) res = res * t % mod ;
b = b >> 1 ;
t = t * t % mod ;
}
return res ;
}
int n , m , a[N] , b[N] ;
LL f0[N][M][M] , f1[N][M][M] , C[M][M] ;// 前i个位置,进行 k 次操作,这个位置的sum为j
int main()
{
scanf("%d%d" , &n , &m ) ;
for(int i = 0 ; i <= m ; i ++ ) {
C[i][0] = 1 ;
for(int j = 1 ; j <= i ; j ++ ) {
C[i][j] = ( C[i-1][j] + C[i-1][j-1] ) % mod ;
}
}
for(int i = 1 ; i <= n ; i ++ ) {
scanf("%d" , &a[i] ) ;
}
for(int i = 1 ; i <= n ; i ++ ) {
scanf("%d" , &b[i] ) ;
}
f0[0][0][0] = 1 ;
for(int i = 0 ; i <= n ; i ++ ) {
for(int k = 0 ; k <= m ; k ++ ) {
// 注意到两种操作其实是独立的,可以分开做
for(int j = a[i] ; j <= min(k,b[i]) ; j ++ ) {
// i,0 -> i+1,1
if( f0[i][k][j] ) {
for(int o = 0 ; o <= j ; o ++ ) { // i+1 位置进行 -1 操作,与前面匹配
f1[i+1][k][j-o] = ( f1[i+1][k][j-o] + f0[i][k][j]*C[j][o] ) % mod ;
}
}
}
for(int j = 0 ; j <= b[i] ; j ++ ) { // 在 i+1 位置进行 p 次 +1 操作
// 0 -> 1
if( f1[i+1][k][j] ) {
for(int p = max(0,a[i+1]-j) ; p <= min(m-k,b[i+1]-j) ; p ++ ) {
f0[i+1][k+p][j+p] = ( f0[i+1][k+p][j+p] + f1[i+1][k][j]*C[m-k][p] ) % mod ;
}
}
}
}
}
printf("%lld" , f0[n+1][m][0] ) ;
return 0 ;
}
T2
首先贴一个来自 tbls 的逆天 GCD,加上后吊打正解 (bushi
inline LL qGcd(LL a, LL b) {
if (!a | !b) {
return a | b;
}
int az = __builtin_ctzll(a), bz = __builtin_ctzll(b), z = min(az, bz);
a >>= az; b >>= bz;
while (a != b) {
LL diff = b - a; az = __builtin_ctzll(diff);
b = min(a, b); a = abs(diff) >> az;
}
return a << z;
}
下面说正解:
baka’s trick 佬のblog
首先我赛时有点唐,编了个不常规但更快的做法 (bushi
正常的想法:同样是按 r r r 枚举,实时维护最靠左的 gcd 不为 1 的位置(而不用维护内部的所有 gcd),实际上是双指针
但 gcd 的限制在于 不可撤销,由于本质是 M i n Min Min 操作,我们 l + + l++ l++ 后没法实时维护出区间 gcd
就像回滚莫队之于普通莫队,这个 trick 使得双指针可以便捷维护这类不可撤销信息
动态维护 l , r , m i d l,r,mid l,r,mid 三个指针,对于 [ l , m i d ] [l,mid] [l,mid] 内我维护从 m i d mid mid 到 l l l 的后缀 gcd,从 m i d + 1 mid+1 mid+1 到 r r r 维护 前缀 gcd,区间 gcd 即可以用 g c d ( f [ l ] , f [ r ] ) gcd(f[l],f[r]) gcd(f[l],f[r]) 得到
r r r 右移时,更新 f [ r ] = g c d ( f [ r − 1 ] , b [ r ] ) f[r]=gcd(f[r-1],b[r]) f[r]=gcd(f[r−1],b[r]) ( m i d + 1 < r ) (mid+1< r) (mid+1<r),然后当区间 gcd = 1 时,移动 l l l
若 l > m i d l>mid l>mid,此时不能再移,那么把 m i d mid mid 移动到 r r r,然后重构 [ l , m i d ] [l,mid] [l,mid] 段内的后缀 gcd,同时更新最靠左的 l l l
int l = 1 , mid = 1 , ans = 1 ;
for(int r = 1 ; r < n ; r ++ ) {
if( r == 1 || mid+1 == r ) f[r] = b[r] ;
else f[r] = Gcd( f[r-1] , b[r] ) ;
while( l <= mid && Gcd(f[r],f[l]) == 1 ) l ++ ;
if( l > mid ) { // 重构
mid = r ;
f[mid] = b[r] ;
if( b[r] == 1 ) {
l = r+1 ;//相当于 k=r
}
else {
for(int k = r-1 ; k >= l ; k -- ) {
f[k] = Gcd( f[k+1] , b[k] ) ;
if( f[k] == 1 ) {
l = k+1 ;
break ;
}
}
}
}
ans = max( ans , r-l+2 ) ;
}
时间复杂度,由于三个指针移动次数是 O ( n ) O(n) O(n),重构次数也是 O ( n ) O(n) O(n),对于这道题复杂度为 O ( n l o g V ) O(nlogV) O(nlogV)
T3
式子题
本题等价于求:
C t x + C 2 t x + C 3 t x . . . + C n t x C_t^x+C_{2t}^x+C_{3t}^x...+C_{nt}^x Ctx+C2tx+C3tx...+Cntx
看到这个形式,容易想到当 t = 1 t=1 t=1 时,是组合数的下指标求和,我们是会做的:
C 1 x + C 2 x + C 3 x + . . . + C n x = C n + 1 x + 1 C_1^x+C_2^x+C_3^x+...+C_n^x=C_{n+1}^{x+1} C1x+C2x+C3x+...+Cnx=Cn+1x+1
这个式子的组合意义是: n + 1 n+1 n+1 个人中选 x + 1 x+1 x+1 个,枚举选择的人中最大的编号,接下来再在前面选 x x x 个
如果是 t = 2 t=2 t=2 呢?我们凑一下
∑ i = 1 n C 2 i x + ∑ i = 1 n C 2 i + 1 x = ∑ i = 1 2 n + 1 C i x − C 1 x \sum_{i=1}^n C_{2i}^x+\sum_{i=1}^n C_{2i+1}^{x}=\sum_{i=1}^{2n+1}C_i^x-C_1^x ∑i=1nC2ix+∑i=1nC2i+1x=∑i=12n+1Cix−C1x ,可以直接算
推广一下:
∑ i = 1 n C t i x + ∑ i = 1 n C t i + 1 x + . . . + ∑ i = 1 n C t i + t − 1 x = ∑ i = 1 t n + t − 1 C i x − ( C 1 x + . . . + C t − 1 x ) \sum_{i=1}^n C_{ti}^x+\sum_{i=1}^n C_{ti+1}^x+...+\sum_{i=1}^n C_{ti+t-1}^x=\sum_{i=1}^{tn+t-1}C_i^x-(C_1^x+...+C_{t-1}^x) ∑i=1nCtix+∑i=1nCti+1x+...+∑i=1nCti+t−1x=∑i=1tn+t−1Cix−(C1x+...+Ct−1x),可以算
我们设 f ( x , r ) = ∑ i = 1 n C t i + r x f(x,r)=\sum_{i=1}^n C_{ti+r}^x f(x,r)=∑i=1nCti+rx,已知 ∑ i = 0 t − 1 f ( x , i ) \sum_{i=0}^{t-1} f(x,i) ∑i=0t−1f(x,i)
接下来再找一些关系,可以发现相邻两项做差可以用组合数性质,即
f ( x , r ) − f ( x , r − 1 ) = f ( x − 1 , r − 1 ) f(x,r)-f(x,r-1)=f(x-1,r-1) f(x,r)−f(x,r−1)=f(x−1,r−1)
把 f ( x , r ) f(x,r) f(x,r) 全部化成 f ( x − 1 , r ) f(x-1,r) f(x−1,r) 和 f ( x , 0 f(x,0 f(x,0) 的形式,带入到 ∑ f \sum f ∑f 的式子即可用 x − 1 x-1 x−1 的所有 求出 ( x , 0 ) (x,0) (x,0),然后递推求 ( x , r ) (x,r) (x,r)
复杂度 O ( n t 2 ) O(nt^2) O(nt2)
T4
神奇数数
我们考虑对于每个连通块找到一个 “代表元”,以此来计数
让一个连通块中 a i + b j a_i+b_j ai+bj 最小的,如果相同取 i i i 更小,如果仍相同取 j j j 更小的作为代表元,数这样的点的数量就是答案
考虑怎样的 ( i , j ) (i,j) (i,j) 可以当作代表元,首先显然有 a i + b j ≤ x a_i+b_j\leq x ai+bj≤x
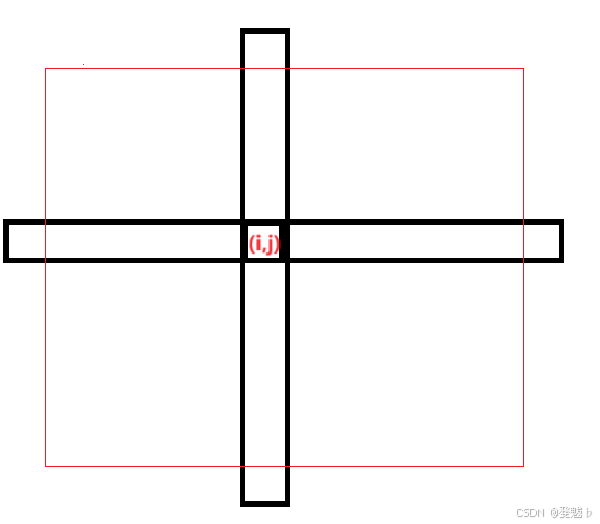
( n n n 作为行, m m m 作为列 ) 接下来找到 ( i , j ) (i,j) (i,j) 左侧第一个 ≤ b j \leq b_j ≤bj 的,右侧第一个 < b j <b_j <bj 的,上方第一个 ≤ a i \leq a_i ≤ai,下方第一个 < a i <a_i <ai,因为这些点是可能 “替代” 这个代表元的
给出一个结论, ( i , j ) (i,j) (i,j) 为代表元,等价于 ( i , j ) (i,j) (i,j) 只走黑块,不能往上、下、左、右走到对应的这四个点中的一个上
充分性:若 ( i , j ) (i,j) (i,j) 为代表元,一旦能走到,说明 ( i , j ) (i,j) (i,j) 与这四个点连通,就会导致 ( i , j ) (i,j) (i,j) 不如这四个点,代表元被替代
必要性:只要走不到这四个点,就一定走不出这个矩形,因为 往上下左右直着走 是最容易走出去的路径 ( 从大小关系容易得出 ) ,那么 ( i , j ) (i,j) (i,j) 所在的连通块就不与外界连通,而这个矩形内没有点比 ( i , j ) (i,j) (i,j) 作为代表元更优,所以 ( i , j ) (i,j) (i,j) 就是这个连通块的代表元
以 a i a_i ai 为例,看 ( i , j ) (i,j) (i,j) 走不到四个点等价于什么:
设左边第一个比 a i a_i ai 大的位置为 L i L_i Li,右边为 R i R_i Ri,那么:
m i n ( m a x ( a L i , . . . a i ) , m a x ( a i , . . . , a R i ) ) + b j > x min(\ max(a_{L_i},...a_i),max(a_i,...,a_{R_i})\ )+b_j > x min( max(aLi,...ai),max(ai,...,aRi) )+bj>x
记前面那一坨为 A i A_i Ai , A i A_i Ai 显然可以 O ( n ) O(n) O(n) 求出,同理定义 B i B_i Bi,那么合法的代表元 ( i , j ) (i,j) (i,j) 满足:
{ a i + b j ≤ x A i + b j > x a i + B j > x \left\{\begin{matrix} a_i+b_j\leq x \\A_i+b_j>x \\a_i+B_j>x \end{matrix}\right. ⎩ ⎨ ⎧ai+bj≤xAi+bj>xai+Bj>x
显然这是一个偏序问题,二维数点扫描线即可
#include<bits/stdc++.h>
using namespace std ;
typedef long long LL ;
const int N = 2e5+100 , INF = 2e5 ;
// 神仙题
int n , m , X , a[N] , b[N] ;
int sta[22][N] , stb[22][N] , Lg2[N] ;
void make_st()
{
for(int i = 2 ; i <= max(n,m) ; i ++ ) Lg2[i] = Lg2[i/2] + 1 ;
for(int i = 0 ; i <= 20 ; i ++ ) {
if( i == 0 ) {
for(int j = 1 ; j <= n ; j ++ ) sta[i][j] = a[j] ;
for(int j = 1 ; j <= m ; j ++ ) stb[i][j] = b[j] ;
}
else {
for(int j = 1 ; j <= n-(1<<i)+1 ; j ++ ) {
sta[i][j] = max( sta[i-1][j] , sta[i-1][j+(1<<(i-1))] ) ;
}
for(int j = 1 ; j <= m-(1<<i)+1 ; j ++ ) {
stb[i][j] = max( stb[i-1][j] , stb[i-1][j+(1<<(i-1))] ) ;
}
}
}
}
int querya( int l , int r )
{
int k = Lg2[r-l+1] ;
return max( sta[k][l] , sta[k][r-(1<<k)+1] ) ;
}
int queryb( int l , int r )
{
int k = Lg2[r-l+1] ;
return max( stb[k][l] , stb[k][r-(1<<k)+1] ) ;
}
int stk[N] , top , A[N] , B[N] ;
struct line
{
int x , y , f ;
}l[2*N] ;
int len , Min = 1e9 ;
void pre_work()
{
for(int i = 1 ; i <= n ; i ++ ) {
while( top && a[i] < a[stk[top]] ) top -- ;
int l = stk[top]+1 ;
if( !top ) A[i] = INF ;
else A[i] = querya( l , i ) ;
stk[++top] = i ;
}
top = 0 ;
for(int i = 1 ; i <= m ; i ++ ) {
while( top && b[i] < b[stk[top]] ) top -- ;
int l = stk[top]+1 ;
if( !top ) B[i] = INF ;
else B[i] = queryb( l , i ) ;
stk[++top] = i ;
}
top = 0 ;
stk[0] = n+1 ;
for(int i = n ; i >= 1 ; i -- ) {
while( top && a[i] <= a[stk[top]] ) top -- ;
int r = stk[top]-1 ;
if( !top ) A[i] = min( A[i] , INF ) ;
else A[i] = min( A[i] , querya(i,r) ) ;
stk[++top] = i ;
}
top = 0 ;
stk[0] = m+1 ;
for(int i = m ; i >= 1 ; i -- ) {
while( top && b[i] <= b[stk[top]] ) top -- ;
int r = stk[top]-1 ;
if( !top ) B[i] = min( B[i] , INF ) ;
else B[i] = min( B[i] , queryb(i,r) ) ;
stk[++top] = i ;
}
for(int i = 1 ; i <= m ; i ++ ) {
l[++len] = {X-B[i]+1,X-b[i]+1,1} ;
l[++len] = {X-b[i]+1,X-b[i]+1,-1} ;
Min = min ( Min , X-B[i]+1 ) ;
}
}
int ida[N] ;
bool cmpa( int x , int y )
{
return a[x]<a[y] ;
}
bool cmpb( line x , line y )
{
return x.x < y.x ;
}
struct BIT
{
int t[2*N] ;
inline int lowbit( int x ) { return x&-x ; }
void add( int p , int x ) { // 后缀
for( ; p <= INF ; p += lowbit(p) ) t[p] += x ;
}
int ask( int p ) {
int res = 0 ;
for( ; p ; p -= lowbit(p) ) res += t[p] ;
return res ;
}
} T ;
LL ans ;
int main()
{
scanf("%d%d%d" , &n , &m , &X ) ;
for(int i = 1 ; i <= n ; i ++ ) scanf("%d" , &a[i] ) , ida[i] = i ;
for(int i = 1 ; i <= m ; i ++ ) scanf("%d" , &b[i] ) ;
make_st() ;
pre_work() ;
sort( ida+1 , ida+n+1 , cmpa ) ;// query
sort( l+1 , l+len+1 , cmpb ) ;// modify
for(int r = Min , i = 1 , j = 1 ; r <= INF ; r ++ ) {
while( j <= len && l[j].x == r ) {
T.add( max(1,l[j].y) , l[j].f ) ;
j ++ ;
}
while( i <= n && a[ida[i]] == r ) {
ans += T.ask( A[ida[i]] ) ;
i ++ ;
}
}
printf("%lld" , ans ) ;
return 0 ;
}