💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
自从人工智能 (AI) 赢得了国际象棋、将棋和围棋等人类职业选手的青睐以来,人们对人工智能的期望一直在急剧增加。人工智能发展如此之快的原因之一是计算机处理速度的大幅提高,这使得在计算机中虚拟快速重复模拟比赛(如奥赛罗、将棋、围棋等)成为可能。最后,人工智能已经获得了超越人类专业人士的力量。同样在控制工程中,如果控制器的增益调谐实验可以在计算机中虚拟执行,那么有望通过类似AI的方法显着提高控制性能。“V-Tiger”是“Virtual Time-response based Iterative Gain Evaluation and Redesign”的缩写,它迭代:1)根据一次性实验数据计算插入某个控制器时闭环系统的虚拟时间响应,2)根据虚拟时间响应测量过冲和建立时间,以及3)评估和重新设计控制器增益,考虑稳定裕度。
关键词 数据驱动控制、时间响应、增益调谐。
V-Tiger是一种自动调整控制器增益的方法,旨在优化建立时间、过冲和稳定性裕度,它使用被控对象输入/输出阶跃响应来设计PID控制器。本方法的优越性在于可以通过计算机模拟来进行控制器调整,从而提高控制性能。
控制领域的发展趋势是数据驱动控制,利用大量的实验数据拟合控制模型,实现更好的控制效果。 V-Tiger使用一次性实验数据计算插入某个控制器时闭环系统的虚拟时间响应。这种基于数据模型的方法不仅速度更快,还可以从实际过程中构建更准确的模型,从而实现更优质的控制效果。
通过V-Tiger方法,可以快速评估和重新设计控制器增益,考虑稳定裕度。其中,稳定裕度是保证闭环系统稳态误差、阻尼比和过冲都在合理范围内的关键因素。在控制系统设计中,经常需要在建立时间、过冲和稳态误差之间做出权衡。而采用V-Tiger方法可以更好地平衡这些因素,从而实现更好的控制效果。
V-Tiger是一种数据驱动的、基于虚拟实验的方法,能够通过迭代计算和控制器增益的重新设计,显著提高控制性能。它是控制领域发展趋势的重要组成部分,将为未来控制系统的设计和优化带来更为广阔的前景。
【V-Tiger项目】旨在开发一种智能方法,自动调整PID控制器的增益(比例Kp、积分Ki、微分Kd)以优化控制系统的性能,特别是在建立时间、过冲、以及稳定性裕度等方面。该研究利用被控对象的阶跃响应特性来指导控制器参数的设计,以下是研究的关键步骤和方法概述:
1. 系统辨识与模型建立
- 阶跃响应测试:首先,对被控对象进行阶跃输入测试,记录输入和输出数据。这一步骤是为了获取系统的动态行为信息,如上升时间、峰值时间、稳态误差等。
- 模型拟合:基于收集的数据,利用系统辨识技术(如最小二乘法、频率响应估计等)来建立被控对象的数学模型,通常采用一阶、二阶或更高阶的传递函数模型。
2. PID控制器参数初估
- 经验公式:根据被控对象模型的参数(如时间常数、阻尼比、自然频率等),应用经验公式(如Ziegler-Nichols方法、Tyreus-Luyben规则等)来初步估计PID控制器的增益值。
- 迭代改进:采用试错方法或更高级的优化算法(如遗传算法、粒子群优化、梯度下降等),逐步调整PID参数,以逼近理想控制性能指标。
3. 性能指标优化
- 建立时间:目标是最短时间达到并保持在设定点附近。
- 过冲:限制输出的最大超出设定点的比例,以避免潜在的风险或不稳定。
- 稳定性裕度:确保系统具有足够的相位裕度和增益裕度,以应对不确定性和扰动,保持长期稳定运行。
4. 闭环性能评估与调整
- 仿真验证:在模型基础上,将PID控制器与被控对象组成闭环系统进行仿真,观察输出响应是否满足性能要求。
- 自适应调整:开发自适应机制,根据闭环系统的实际表现(如通过在线监控输出响应的实时变化),动态调整PID参数,实现持续优化。
5. 实验验证
- 硬件在环(HIL)测试:在实验室环境下,通过HIL系统模拟真实工况,验证优化后的PID控制器性能,确保理论成果的实用性和有效性。
6. 结论与应用
- 分析研究结果,总结自适应调整算法的有效性,探讨其在不同工业过程控制中的适用性和局限性。
- 推广应用:将优化后的控制器算法部署到实际工业控制系统中,提升控制效率和产品质量。
技术挑战与未来展望
- 复杂系统的建模:对于高度非线性、时变或大延迟的系统,模型建立和控制器设计将更加复杂。
- 在线学习与自适应性:开发更为智能的算法,使控制器能实时适应环境变化和系统参数漂移。
- 大数据与机器学习整合:结合大数据分析和深度学习技术,自动从海量历史数据中学习最优控制器参数,提升控制精度和鲁棒性。
📚2 运行结果
主函数代码:
ts=0.01; % sampling time [s]
s=tf('s'); % complex variable of Laplace transform
z=tf('z',ts); % shift operator
p=(1-1/z)/ts; % differential operator based on backward Euler's rule
Gs = 5/(0.01*s^2+0.2*s+10)*exp(-0.1*s); % plant G(s) to be controlled
G = c2d(Gs,ts); % G(z) is derived by discretizing G(s) with zero order holder
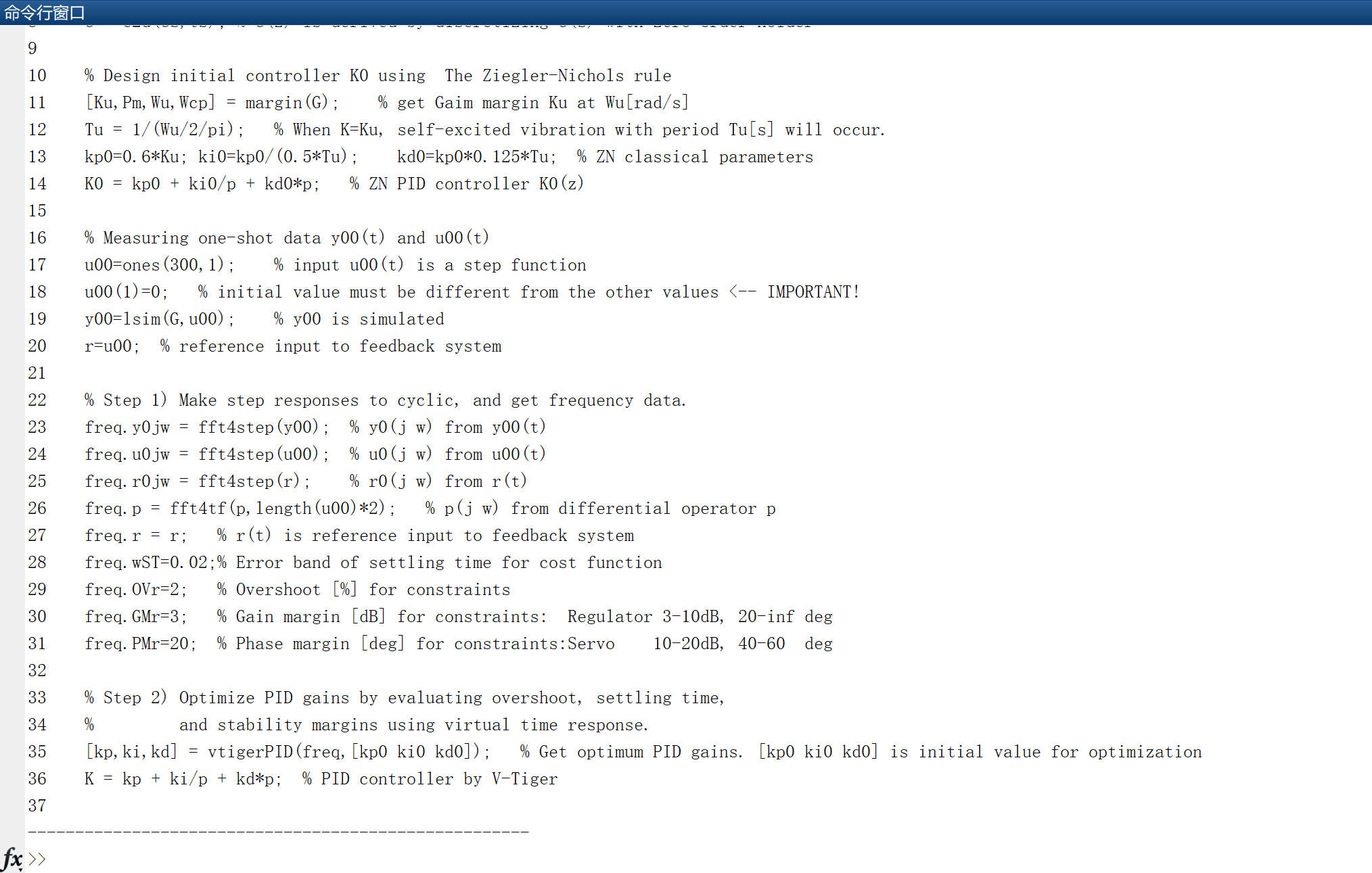
% Design initial controller K0 using The Ziegler-Nichols rule
[Ku,Pm,Wu,Wcp] = margin(G); % get Gaim margin Ku at Wu[rad/s]
Tu = 1/(Wu/2/pi); % When K=Ku, self-excited vibration with period Tu[s] will occur.
kp0=0.6*Ku; ki0=kp0/(0.5*Tu); kd0=kp0*0.125*Tu; % ZN classical parameters
K0 = kp0 + ki0/p + kd0*p; % ZN PID controller K0(z)
% Measuring one-shot data y00(t) and u00(t)
u00=ones(300,1); % input u00(t) is a step function
u00(1)=0; % initial value must be different from the other values <-- IMPORTANT!
y00=lsim(G,u00); % y00 is simulated
r=u00; % reference input to feedback system
% Step 1) Make step responses to cyclic, and get frequency data.
freq.y0jw = fft4step(y00); % y0(j w) from y00(t)
freq.u0jw = fft4step(u00); % u0(j w) from u00(t)
freq.r0jw = fft4step(r); % r0(j w) from r(t)
freq.p = fft4tf(p,length(u00)*2); % p(j w) from differential operator p
freq.r = r; % r(t) is reference input to feedback system
freq.wST=0.02;% Error band of settling time for cost function
freq.OVr=2; % Overshoot [%] for constraints
freq.GMr=3; % Gain margin [dB] for constraints: Regulator 3-10dB, 20-inf deg
freq.PMr=20; % Phase margin [deg] for constraints:Servo 10-20dB, 40-60 deg
% Step 2) Optimize PID gains by evaluating overshoot, settling time,
% and stability margins using virtual time response.
[kp,ki,kd] = vtigerPID(freq,[kp0 ki0 kd0]); % Get optimum PID gains. [kp0 ki0 kd0] is initial value for optimization
K = kp + ki/p + kd*p; % PID controller by V-Tiger
disp('-----------------------------------------------------')
% Verify the controller of V-Tiger and ZN by simulations
[y,u] = freq2yu(freq,K); % Virtual time responses predicted by V-Tiger when K is used
Gcl = feedback(ss(G*K),1); % closed loop transfer function. feedback(a,b)=a/(1+a*b). ss(G) is ss(Gcl); % State space representation from G
yt=lsim(Gcl,r); % yt is true y(t) simulated using true plant model G(z)
yZN=lsim(feedback(ss(G*K0),1),r);% y(t) by K0 (ZN) is simulated using true plant model G(z)
figure(1),
p1=plot([yt yZN y-yt y00]);
hold on
vtigerPID(freq,[kp ki kd],1);
hold off; grid; xlabel('sample number k (0.01k [sec])')
legend(p1,'y (V-Tiger)','y (ZN)','error of true/virtual y','y_{00}','Location','southeast');
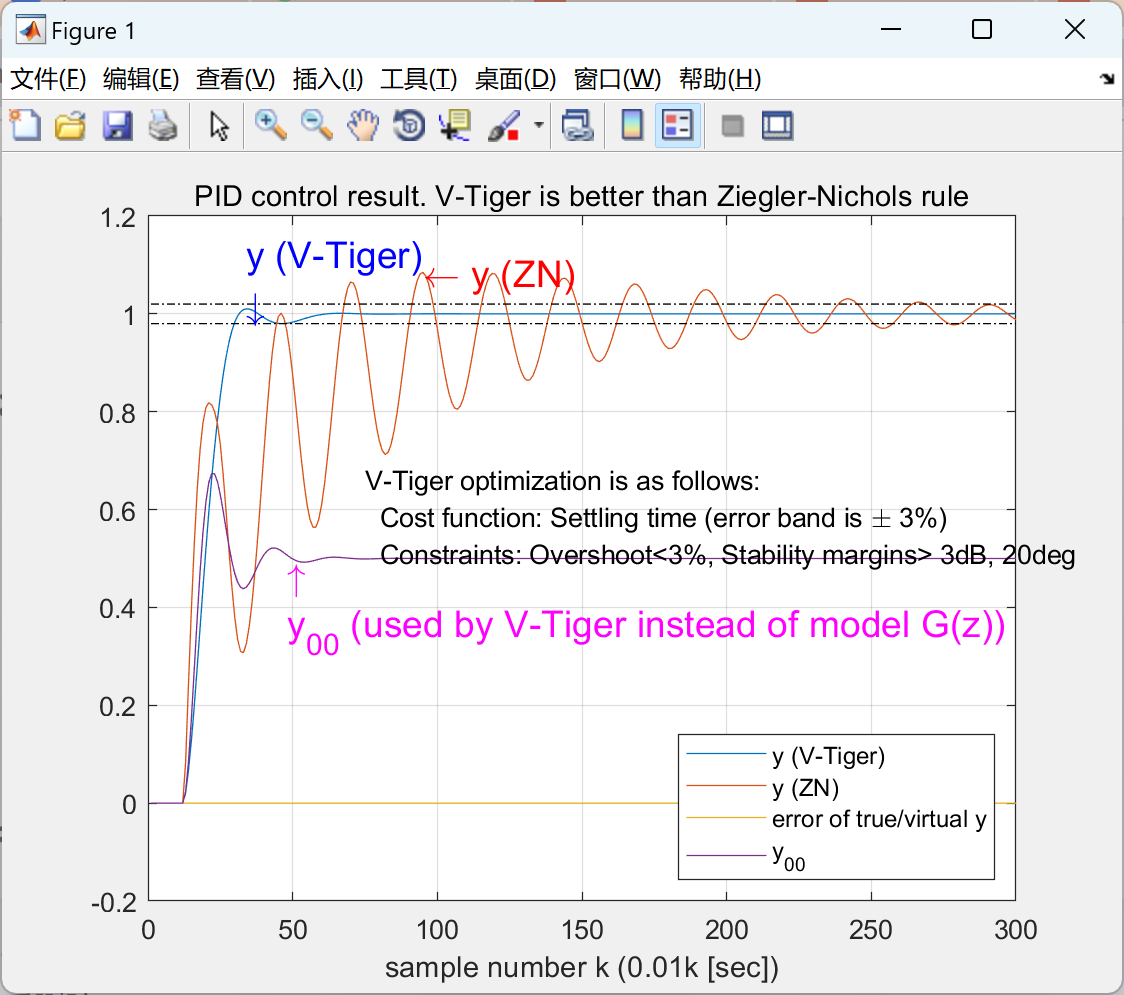
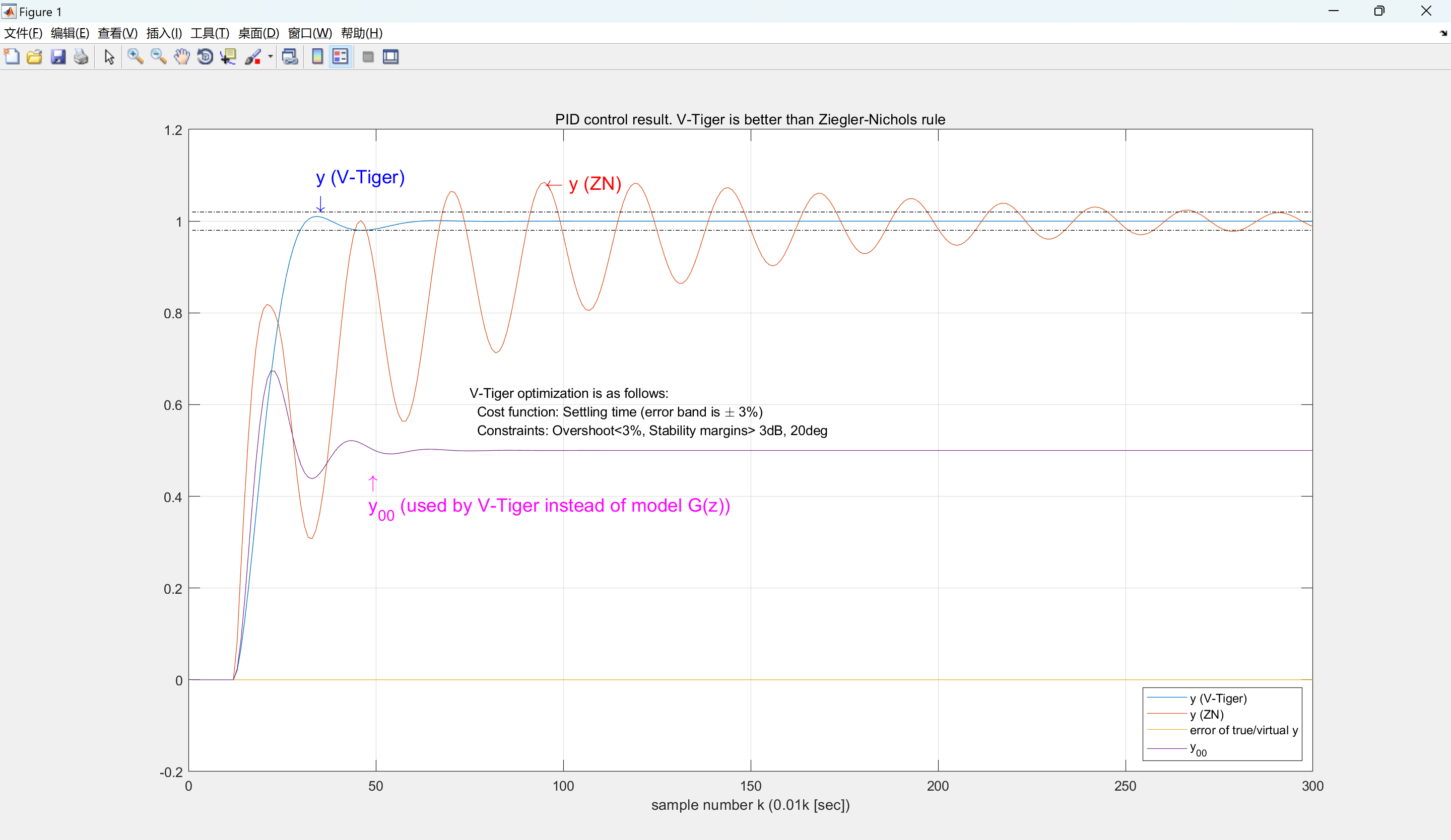
title('PID control result. V-Tiger is better than Ziegler-Nichols rule')
disp('V-Tiger has completed controller design using y00 instead of the plant model.')
disp(['Plant G(s) to be discretized with sampling time ts=' num2str(ts) '[s] is as follows:']),
[yZN,iZN]=max(yZN); text(iZN,yZN,'\leftarrow y (ZN)','Color','red','FontSize',14);
[yvt,ivt]=max(yt); text(ivt,yvt+0.06,['y (V-Tiger)';'\downarrow '],'Color','blue','FontSize',14);
text(length(y)*0.16,y00(end)*0.8,['\uparrow '; ...
'y_{00} (used by V-Tiger instead of model G(z))'],'Color','magenta','FontSize',14);
text(length(y)*0.25,max(y)*0.58,[ ...
'V-Tiger optimization is as follows: '; ...
' Cost function: Settling time (error band is \pm 3%) '; ...
' Constraints: Overshoot<3%, Stability margins> 3dB, 20deg'])
Gs, disp('');
disp('Fig.1 shows step resonses. V-Tiger is better than ZN method.'),
disp('press any key to type code of "vtiger_demo.m".'),
pause
disp('-----------------------------------------------------')
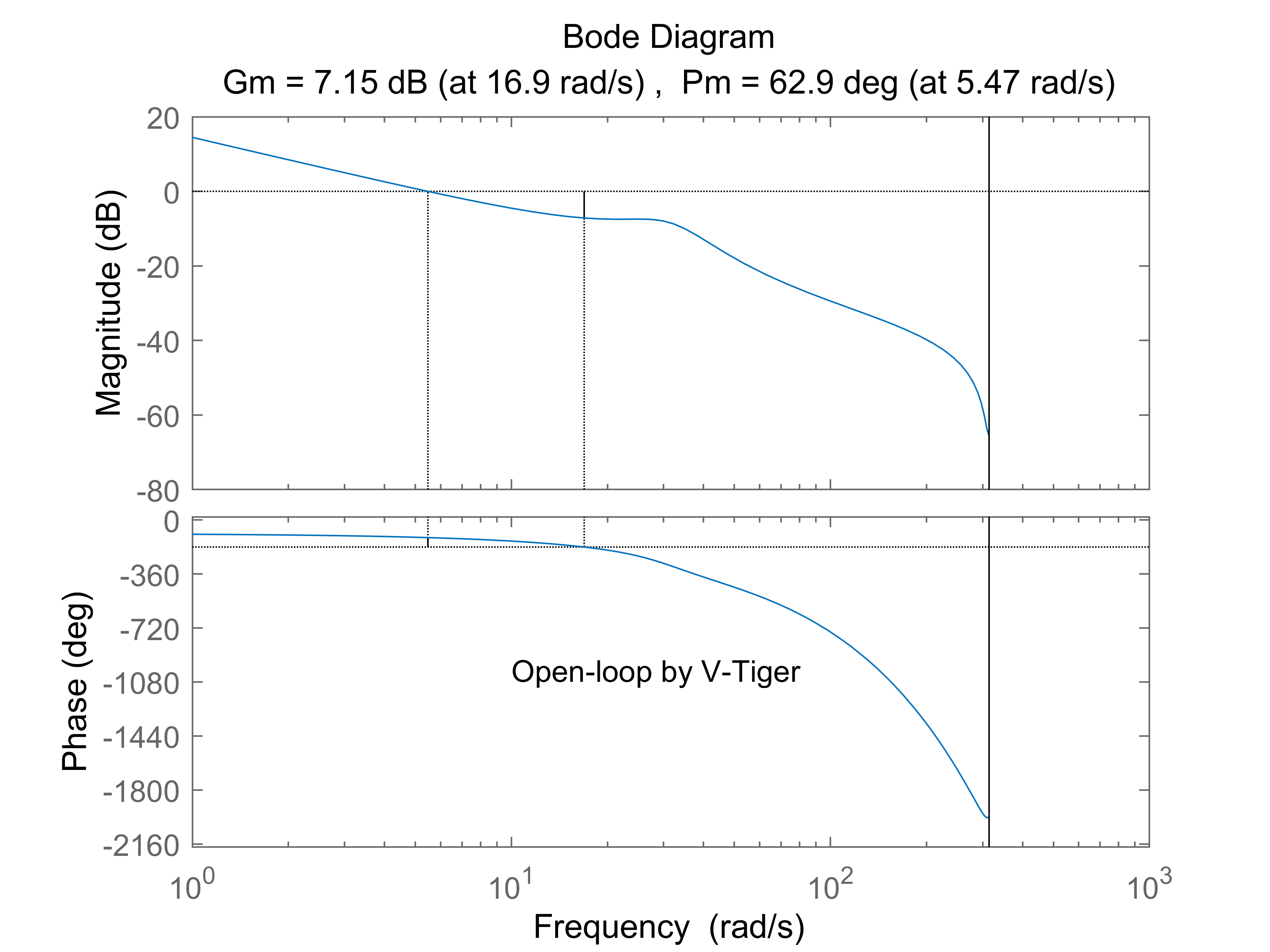
figure(2), margin(G*K); text(10,-1000,'Open-loop by V-Tiger')
dbtype vtiger_demo 1:37
disp('-----------------------------------------------------')
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]李普贤.大滞后系统控制器的设计及性能评估[D].北京化工大学,2017.DOI:CNKI:CDMD:2.1017.288686.
[2]李刚,WANG,Qing-lin.基于阶跃跟踪响应的PID控制器性能评价与调节[J].系统仿真学报, 2008.DOI:JournalArticle/5aed4d1fc095d710d40a9782.
[3]王海燕,燕巍.一种自整定PID参数的模糊控制系统的设计与仿真[J].自动化技术与应用, 2015.DOI:JournalArticle/5b3bb7b8c095d70f008a1d1f.