1. 适用于动态规划解决问题得特征
-
最优化原理
是指一个问题的最优解,包括其子问题的最优解,或一个最优化策略的子策略总时最优的
-
无后向行
及某个阶段的状态一旦确定,求不受这个状态以后策略的影响
-
子问题重叠
即:子问题之间是不独立的,一个子问题在下一个阶段的决策中可能被多次使用到;
2. 动态规划的基本思想
1. 将求解的问题分成多个阶段或多个子问题,然后按顺序求解各子问题;前一子问题的解为后一子问题的解提供了有用的信息;
2. 在求解任意子问题时,列出各种可能的局部解,通过决策表六那些有可能达到最优的局部解,丢弃其他的局部解
3. 由于动态规划解决的问题多数有重叠子问题这个特点,为了减少重复计算,对每一个子问题只求解一次,将其不同阶段的不同状态保存搭配一个二维数组中
3. 设计动态规划的步骤
-
划分阶段
-
选择状态
-
确定决策并写出状态转移方程
4. 资源分配问题
1. 题目:
设有资源n,(n为整数),分配给m各项目,gi(x)为第i各项目分得资源x(x为整数)所得到得利润;求总利润最大得资源分配方案,也就是求下面问题
max z = g1(x1) + g2(x2) + ....+ gm(xm)
x1 + x2 + x3 + .... + xm = n, 0<= xi <= n ,且xi为整数,i = 1,2,3 ...,m
2. 算法设计
-
划分阶段
将该问题划分为A,B,C三个阶段
-
选择状态
例:第一阶段A 有8种情况 分别是 x1(x1表示给A分配得钱数) =0,1,2,....,7、
第二个阶段(A,B)有8中情况,分别是x2(x2表示给A,B分得得钱数) = 0,1,2,.....,7
-
决定决策并写出状态转移方程
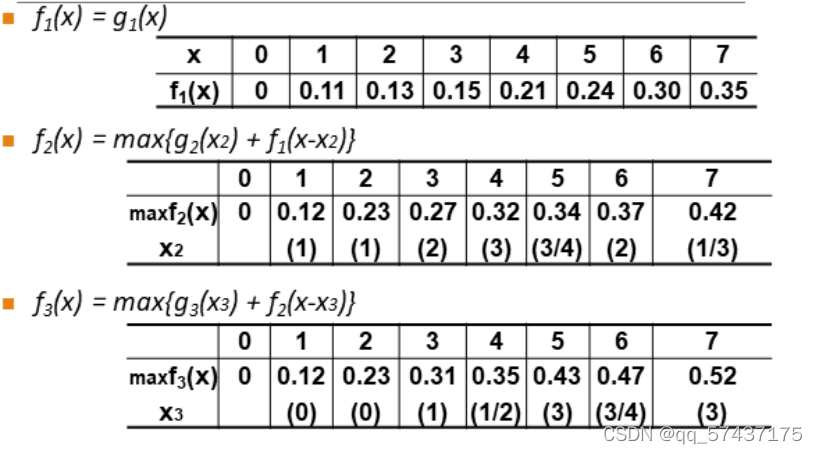
状态转移方程 max{ p(x) + f(n-x)} 解释一下:x表示在该阶段 i ,给 i 阶段(A,B,或C)的钱,n表示总的投资金额
f(n-x)表示 i - 1阶段的最优子结构
-
算法实现程序
以下图片就是a中所能存储的数据,但是要注意:这个算法真的很神奇,就是实现之后,你如果手头有5万元,而不仅仅是7万元,你也可以求出最优解
解释一下a(以这个题为例讲解),a中所存储的是一、二、三 阶段 的最优解,而不仅仅是A、B、C的最优解,重要的是 阶段
阶段:第一节段最优解是指给A投资的最优解
第二阶段最优解是指给A、B投资的最优解
第三阶段最优解是指给A、B、C投资的最优解
所以可以由a中得出,投资 总额 和 每个 项目所投资的数的关系,不要被着题给限制住了,这个算法十分强大,不仅仅可以求解投资总额为7的最优解,也可以求解投资总额为1,.....,6的解,当然你也可以进行算法改进求投资总额为100万元的都没问题,不过由于题目信息的限制,题中只给出了给A,B,C投资1~7的利润值
#include<stdio.h>
void main() {
//主方法要尽可能的简化
//a中存放每一状态的最优的解,p中存放每A,B,C的利润,f记录当前项目的最大利润
//m表示项目数,n表示总的投资额
/*
* m = 3;n = 7
A:0 0.11 0.13 0.15 0.21 0.24 0.30 0.35
B:0 0.12 0.16 0.21 0.23 0.25 0.24 0.34
C:0 0.08 0.12 0.20 0.24 0.26 0.30 0.35
*/
//起始下标均为0,也可以自己设置为1
int a[3][8],m,n,rest,gain[9],t;
float p[8], f[8], temp[8];
printf("请输入项目数:"); scanf_s("%d", &m);
printf("请输入总的投资金额:"); scanf_s("%d", &n);
//初始化状态一的
printf("请输入A的利润:");
for (int i = 0; i <= n; i++) {
scanf_s("%f", &p[i]);
f[i] = p[i];
}
for (int i = 0; i <= n; i++) {
a[0][i] = i;
}
//开始解决剩余的m-1各项目,先对这n-1项进行初始化
for (int k = 1; k < m; k++) {
printf("请输入第%d个项目的利润:",k+1);
for (int j = 0; j <= n; j++) {
temp[j] = 0;
scanf_s("%f", &p[j]);
a[k][j] = 0;
}
//我愿称之为精髓
for (int i = 0; i <= n; i++) {//i表示给这个阶段投的总钱数
for (int j = 0; j <= i; j++) {//j表示给这个阶段的比较主体投的钱数(即第一阶段的比较主体为A;第二阶段的比较主体为B;第三阶段的比较主体为C)
//以下的比较思想尤为重要
//1. p[j] + f[i-j] 状态转移方程
//2. temp[i]中存放该阶段中,当投资总额为i时的最优子结构,起始的时候,将temp设置为0,保证temp中最终存放的数为该阶段中最优的解
if (p[j] + f[i-j] > temp[i]) {//通过这筛选条件我们可以得出该阶段中,投资总额为i时得最优解
temp[i] = f[i-j] + p[j];
a[k][i] = j;//标号k表示, 第k个项目 ;i表示为该阶段投的总的钱数,j表示给这个阶段的主体所投的钱数
}
}
}
for (int j = 0; j <= n; j++) {
f[j] = temp[j];
}
for (int i = 0; i < 8; i++) {
printf("%f\t", f[i]);
}
printf("\n");
}
/*printf("C:%d", a[2][n]); t = 7 - a[2][n];//还剩下t钱
printf("B:%d", a[1][t]); t = t - a[1][t];
printf("A:%d", a[0][t]);*/
t = n;
for (int i = m-1; i >=0 ; i--) {
gain[i] = a[i][t];//gain中装载回溯之后 所有项目实际投资的金额
t = t - a[i][t];//表示上一阶段回溯后,后阶段所剩的钱数
}
for (int i = 0; i < m; i++) {
printf("第%d个项目的投资额:%d", i+1, gain[i]);
printf("\n");
}
}