快速排序

快速排序是对冒泡排序的一种改进。它的基本思想是∶通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

需求∶
排序前:{6,1，2,7，9，3,4,5,8}

排序后:{1,2,3，4,5,6,7，8,9}

排序原理︰
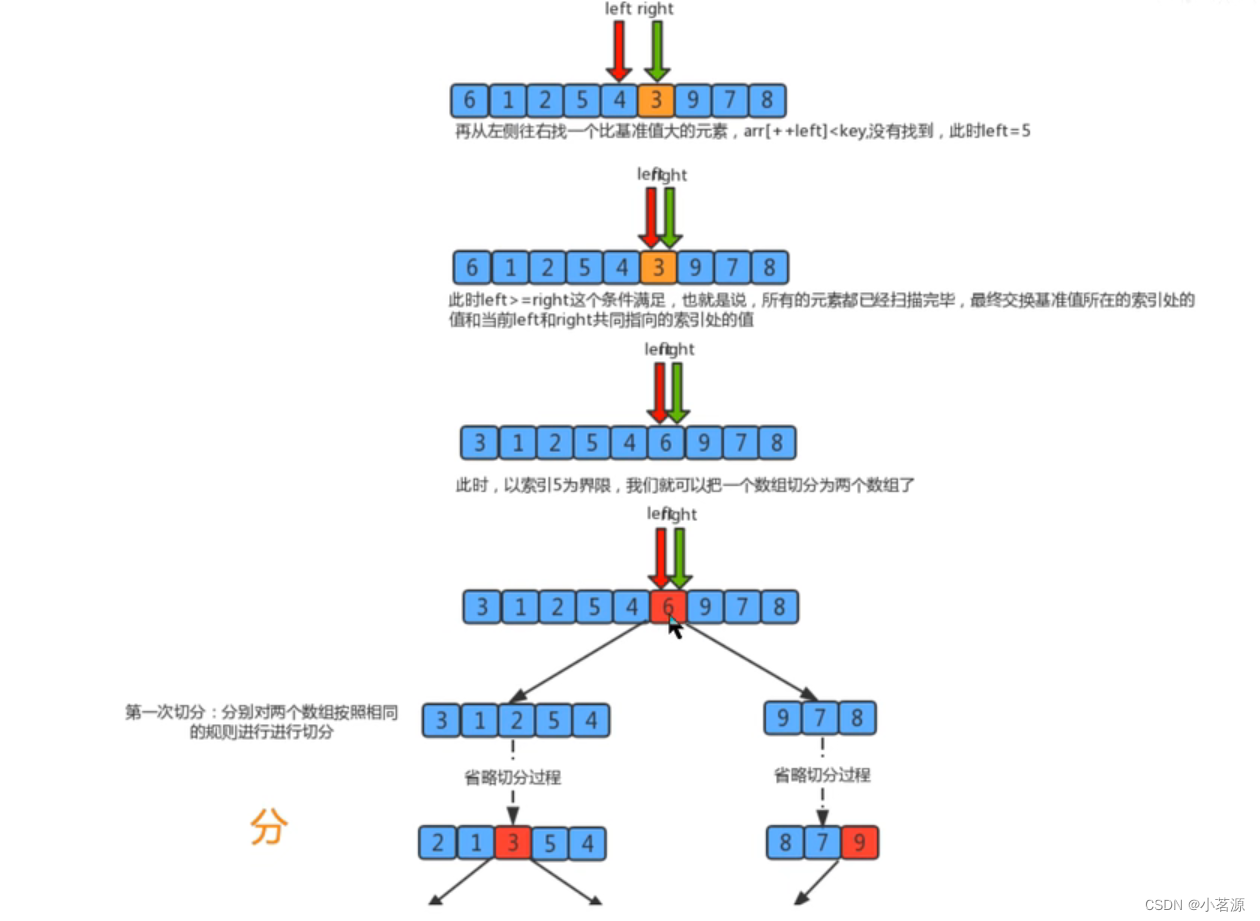
1.首先设定一个分界值，通过该分界值将数组分成左右两部分;
2将大于或等于分界值的数据放到到数组右边，小于分界值的数据放到数组的左边。此时左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值;
3.然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。
4.重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左侧和右侧两个部分的数据排完序后，整个数组的排序也就完成了。

图解:

快速排序API设计:

切分原理:

把一个数组切分成两个子数组的基本思想∶

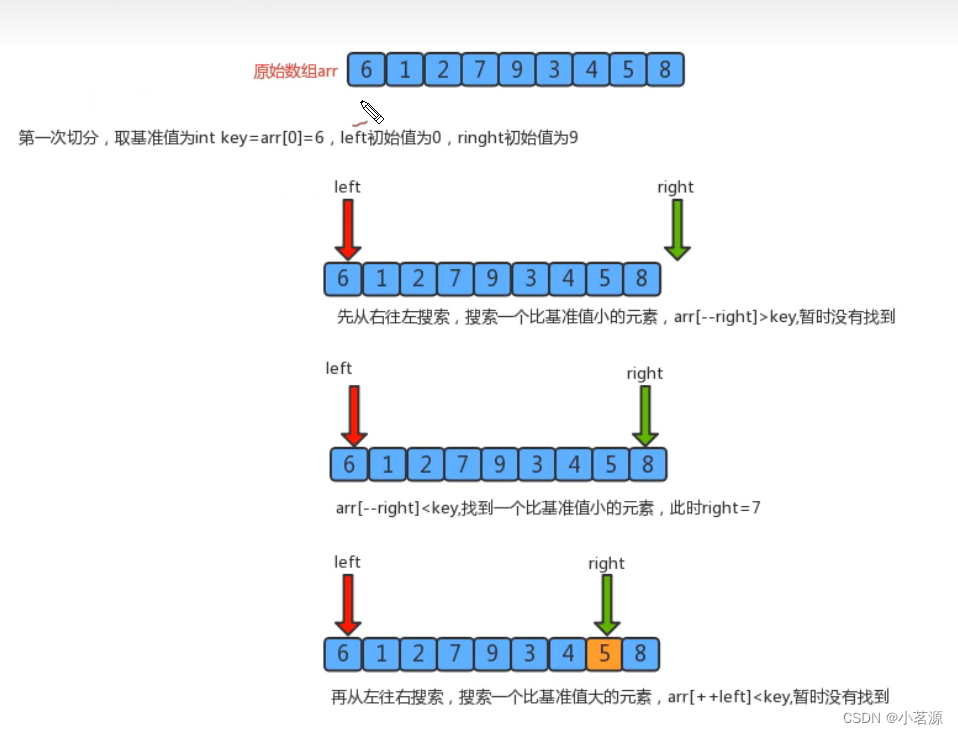
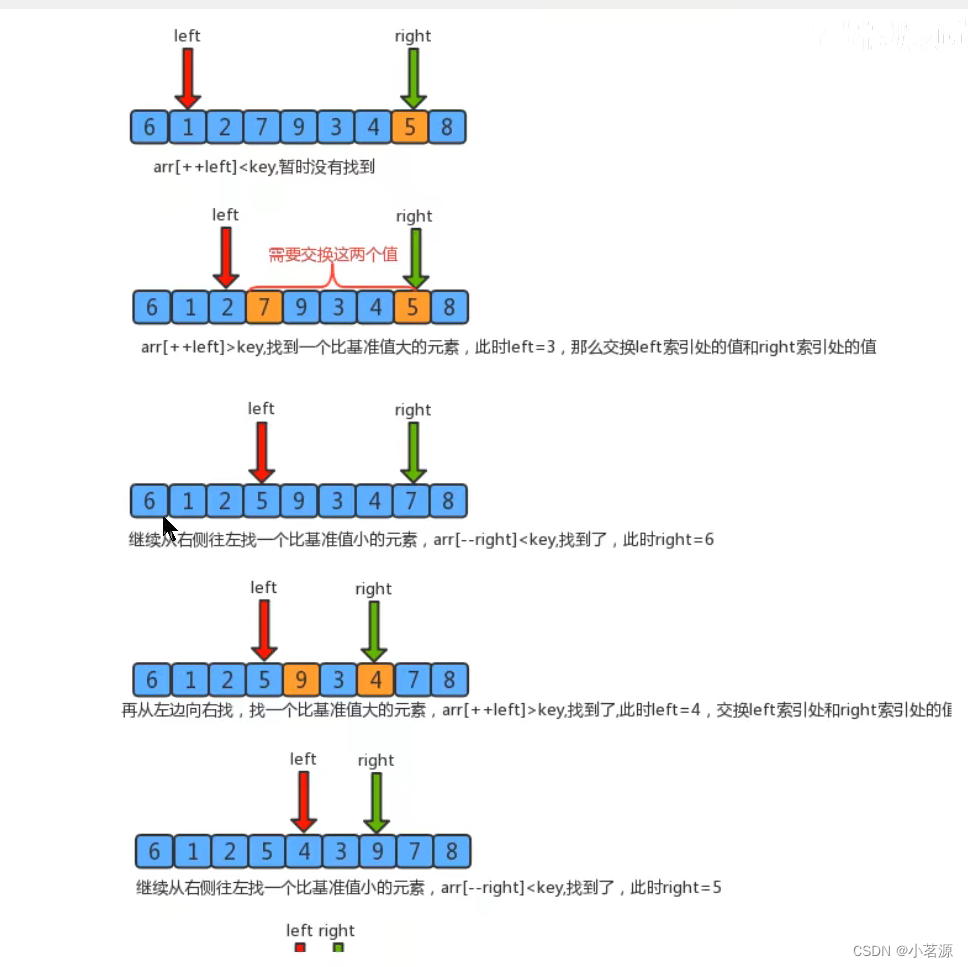
1.找一个基准值，用两个指针分别指向数组的头部和尾部;

2.先从尾部向头部开始搜索一个比基准值小的元素，搜索到即停止，并记录指针的位置;

3.再从头部向尾部开始搜索一个比基准值大的元素，搜索到即停止，并记录指针的位置;

4.交换当前左边指针位置和右边指针位置的元素;

5.重复2,3,4步骤，直到左边指针的值大于右边指针的值停止。

图解:

代码部分:

package com.igeek.sort;

public class Quick {
        /*
            比较v元素是否小于w元素
         */
        private static boolean less(Comparable v,Comparable w){
            return v.compareTo(w)<0;
        }

        /*
            数组元素i和j交换位置
         */
        private static void exch(Comparable[] a,int i,int j){
            Comparable t=a[i];
            a[i]=a[j];
            a[j]=t;
        }

        /*
            对数组a中的元素进行排序
     */
        public static void sort(Comparable[] a){
            int lo=0;
            int hi=a.length-1;
            sort(a,lo,hi);
        }

        /*
            对数组a中从lo到hi的元素进行排序
         */
        private static void sort(Comparable[] a,int lo, int hi){
            //做安全性校验;
            if (hi<=lo){
                return;
            }
            //需要对数组中lo索引到hi索引处的元素进行分组(左子组和右子组);
            int partition=partition(a,lo,hi);//放回的是分组的分界值所在的索引,分界值位置变换后的索引

            //让左子组有序
            sort(a,lo,partition-1);
            //让右子组有序
            sort(a,partition+1,hi);

        }
        /*
            对数组中,从lo到mid为一组,从mid+1到hi为一组,对这俩组数据进行归并
         */
        private static int partition(Comparable[] a,int lo,int hi){
            //确定分界值
            Comparable key=a[lo];
            //定义俩个指针,分别指向待切分元素的最小索引处和最大索引处的下一个位置
            int left=lo;
            int right=hi+1;

            //切分
            while (true){
                //先从右往左扫描,移动right指针,找到一个比分界值大的元素,停止
                while (less(key,a[--right])){
                    if (right==lo){
                        break;
                    }
                }
                //再从左往右扫描,移动left指针,找到一个比分界值大的元素,停止
                while (less(a[++left],key)){
                    if (left==hi){
                        break;
                    }
                }
                //判断left>=right,如果是.则证明元素扫描完毕,结束循环,如果不是,则交换元素即可
                if (left>=right){
                    break;
                }else {
                    exch(a,left,right);
                }
            }
            //交换分界值
            exch(a,lo,right);
           return right;
        }
    }

//测试:
package com.igeek.test;

import com.igeek.sort.Quick;

import java.util.Arrays;

public class QuickTest {
    public static void main(String[] args) {
        Integer[] a={6,1,2,7,9,3,4,5,8};
        Quick.sort(a);
        System.out.println(Arrays.toString(a));
    }
}
//结果:[1, 2, 3, 4, 5, 6, 7, 8, 9]

快速排序和归并排序的区别:

快速排序是另外一种分治的排序算法，它将一个数组分成两个子数组，将两部分独立的排序。快速排序和归并排序是互补的∶归并排序将数组分成两个子数组分别排序，并将有序的子数组归并从而将整个数组排序，而快速排序的方式则是当两个数组都有序时，整个数组自然就有序了。在归并排序中，一个数组被等分为两半，归并调用发生在处理整个数组之前，在快速排序中，切分数组的位置取决于数组的内容，递归调用发生在处理整个数组之后。

快速排序时间复杂分析:

快速排序的一次切分从两头开始交替搜索，直到left和right重合，因此，一次切分算法的时间复杂度为o(n),但整个快速排序的时间复杂度和切分的次数相关。

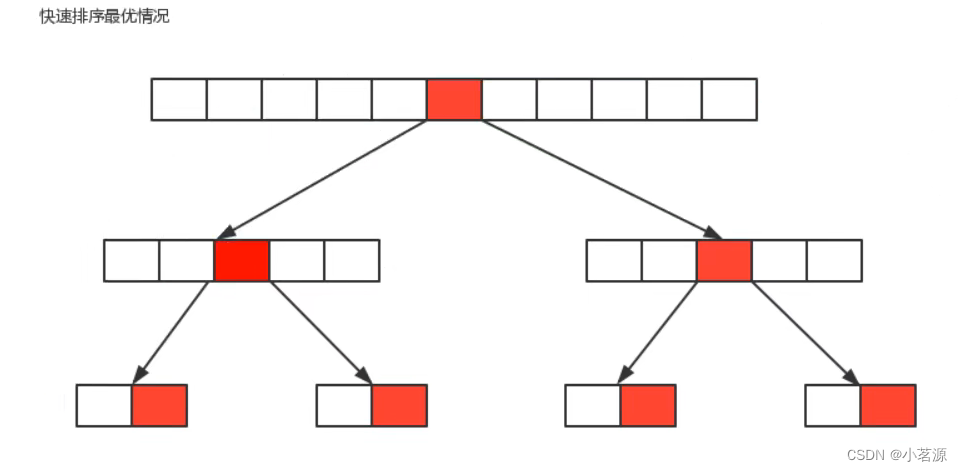
最优情况∶每一次切分选择的基准数字刚好将当前序列等分。

如果我们把数组的切分看做是一个树，那么上图就是它的最优情况的图示，共切分了]o:n次，所以，最优情况下快速排序的时间复杂度为O(nlogn)

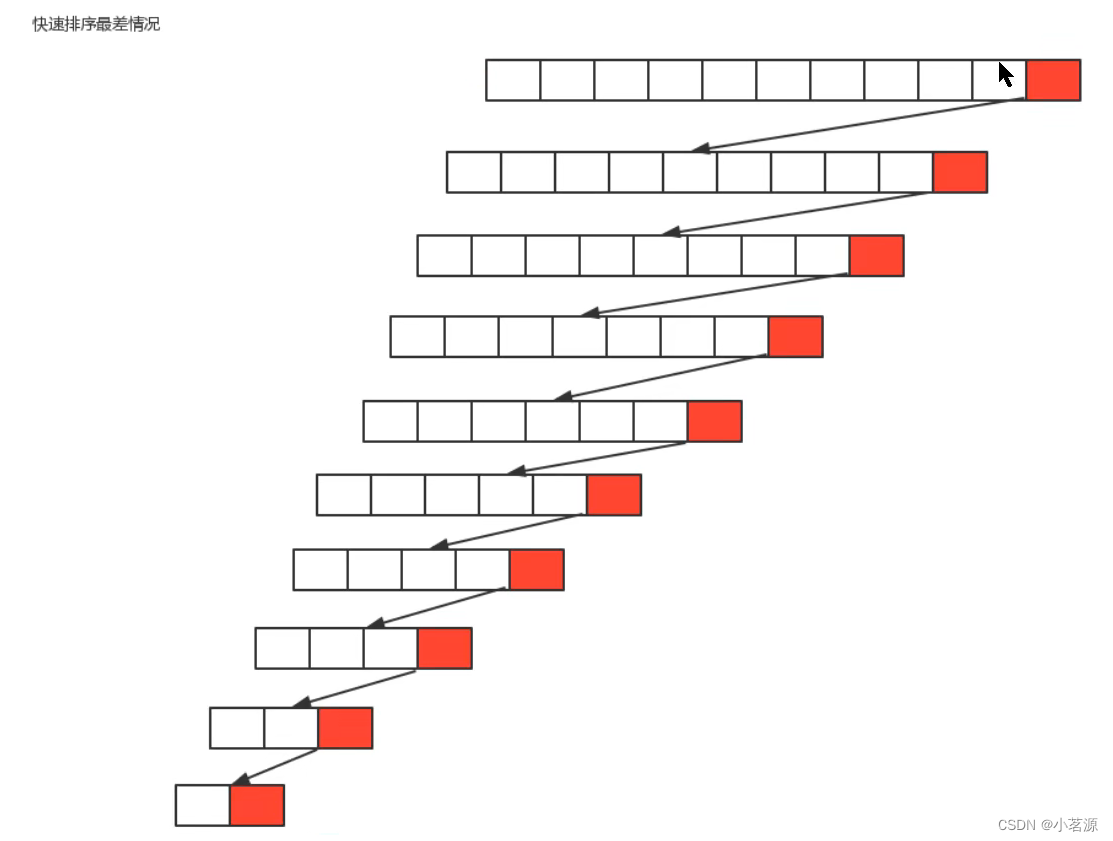
最坏情况∶每一次切分选择的基准数字是当前序列中最大数或者最小数，这使得每次切分都会有一个子组，那么总共就得切分n次，所以，最坏情况下，快速排序的时间复杂度为O(n个2);

平均情况:每一次切公选择的甚准数字不具最大值和最小值，也不是中值，这种情况我们也可以用数学归纳法证明，快速排序的时间复杂度为o(nlogn).由于数学归纳法有很多数学相关的知识，容易使我们混抡，所以这里就不对平均情况的时间复杂度做证明了。

排序的稳定性:

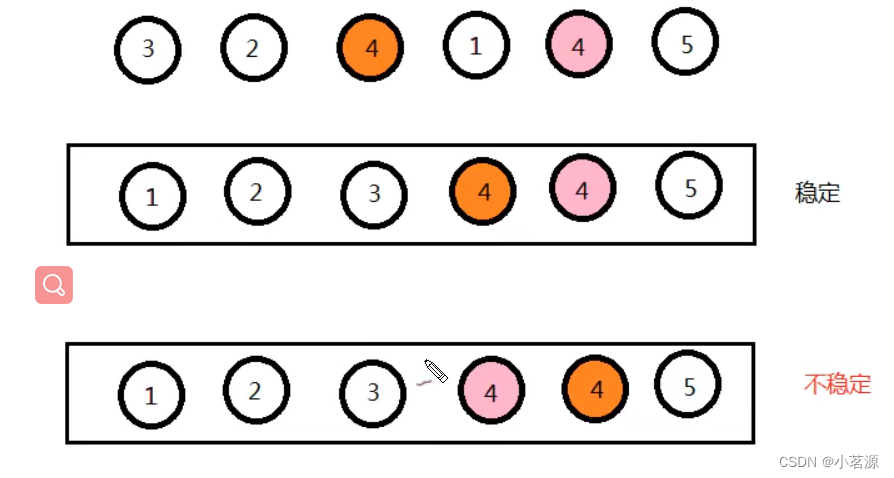
稳定性的定义:

数组arr中有若干元素，其中A元素和B元素相等。并且A元素在B元素前面,如果使用某种排序算法排序后，能够保证A元素依然在B元,素的前面，可以说这个该算法是稳定的。

稳定性的意义:

如果一组数据只需要一次排序，则稳定性一般是没有意义的，如果一组数据需要多次排序，稳定性是有意义的。例如要排序的内容是一组商品对象，第一次排序按照价格由低到高排序，第二次排序按照销量由高到低排序，如果第二次排序使用稳定性算法，就可以使得相同销量的对象依旧保持着价格高低的顺序展现，只有销量不同的对象才需要重新排序。这样既可以保持第一次排序的原有意义，而且可以减少系统开销。

常见排序算法的稳定性:

冒泡排序:

只有当arr[i]>arr[i+1]的时候，才会交换元素的位置，而相等的时候并不交换位置，所以冒泡排序是一种稳定排序算法。

选择排序:

选择排序是给每个位置选择当前元素最小的,，例如有数据{5(1)，8，5(2)，2，9},第一遍选择到的最小元素为2

所以5(1)会和2进

行交换位置，此时5(1)到了5(2)后面，破坏了稳定性，所以选择排序是一种不稳定的排序算法。

插入排序︰

比较是从有序序列的末尾开始，也就是想要插入的元素和已经有序的最大者开始比起，如果比它大则直接插入在其后面，否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的，那么把要插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。

希尔排序:

希尔排序是按照不同步长对元素进行插入排序,虽然一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以希尔排序是不稳定的。

归并排序:

归并排序在归并的过程中，只有arrli]arr[i+1]的时候才会交换位置，如果两个元素相等则不会交换位置，所以它并不会破坏稳定性，归并排序是稳定的。

快速排序︰

:

希尔排序是按照不同步长对元素进行插入排序,虽然一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以希尔排序是不稳定的。

归并排序:

归并排序在归并的过程中，只有arrli]arr[i+1]的时候才会交换位置，如果两个元素相等则不会交换位置，所以它并不会破坏稳定性，归并排序是稳定的。

快速排序︰

快速排序需要一个基准值，在基准值的右侧找一个比基准值小的元素，在基准值的左侧找一个比基准值大的元素，然后交换这两个元素，此时会破坏稳定性，所以快速排序是一种不稳定的算法。