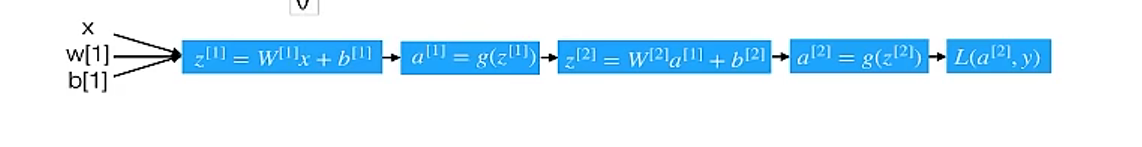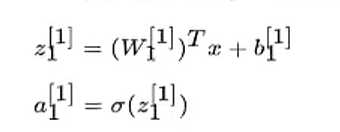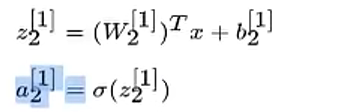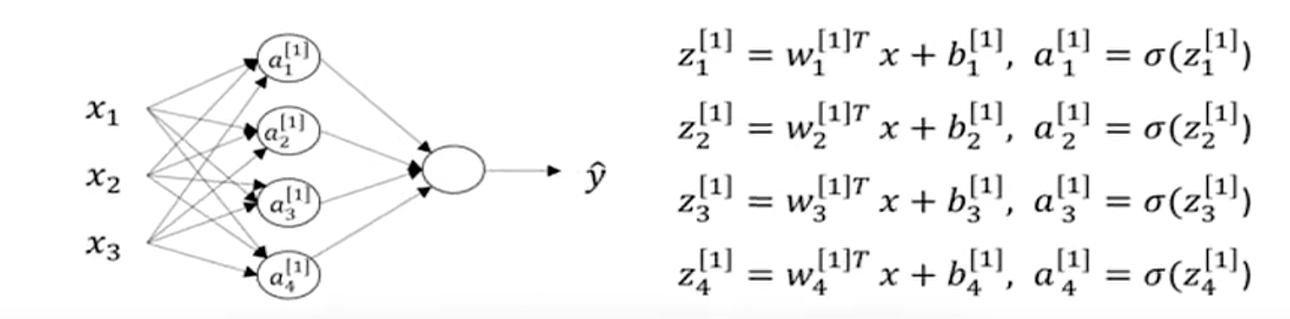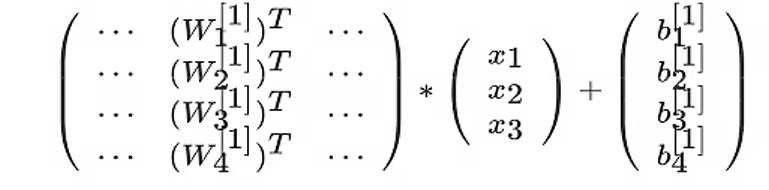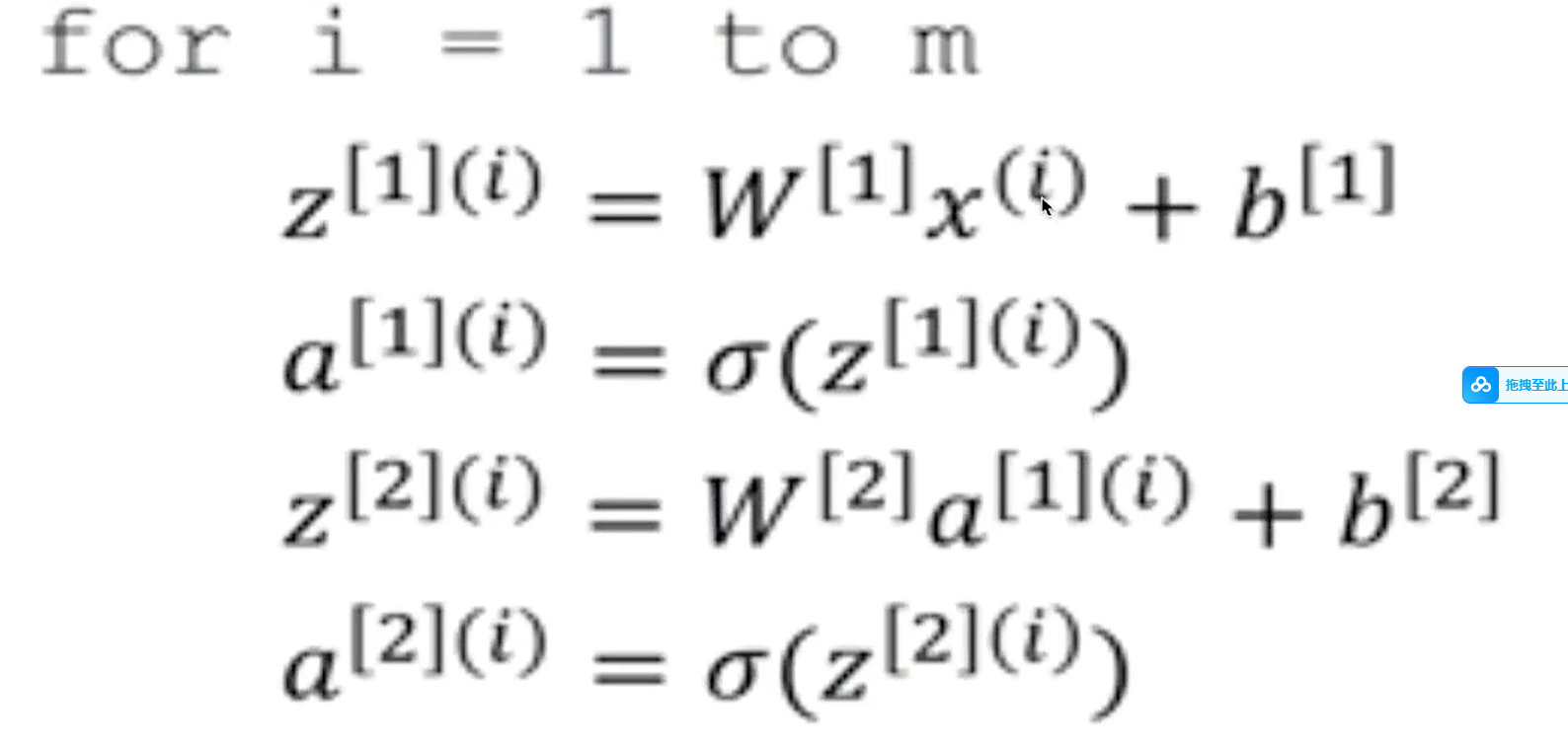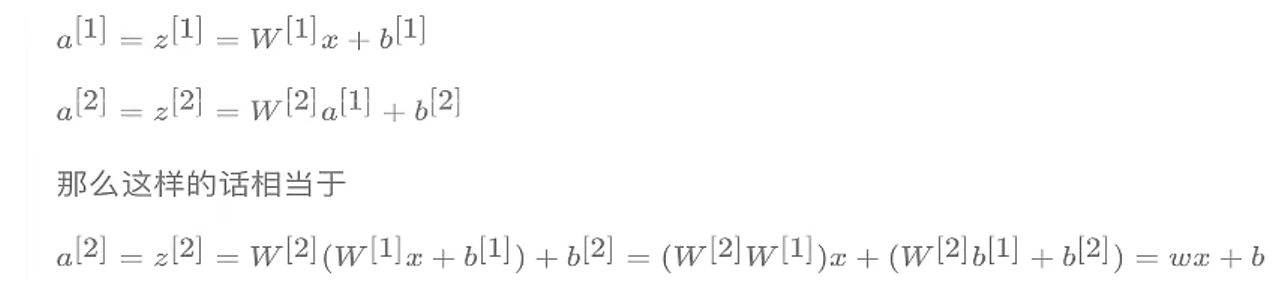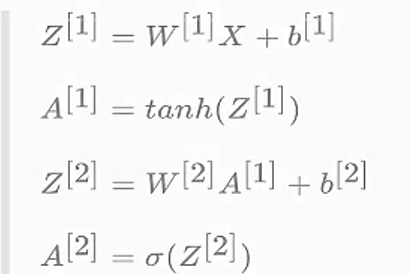目录
1.3.5 练习
1.3.浅层神经网络
1.3.1 浅层神经网络表示
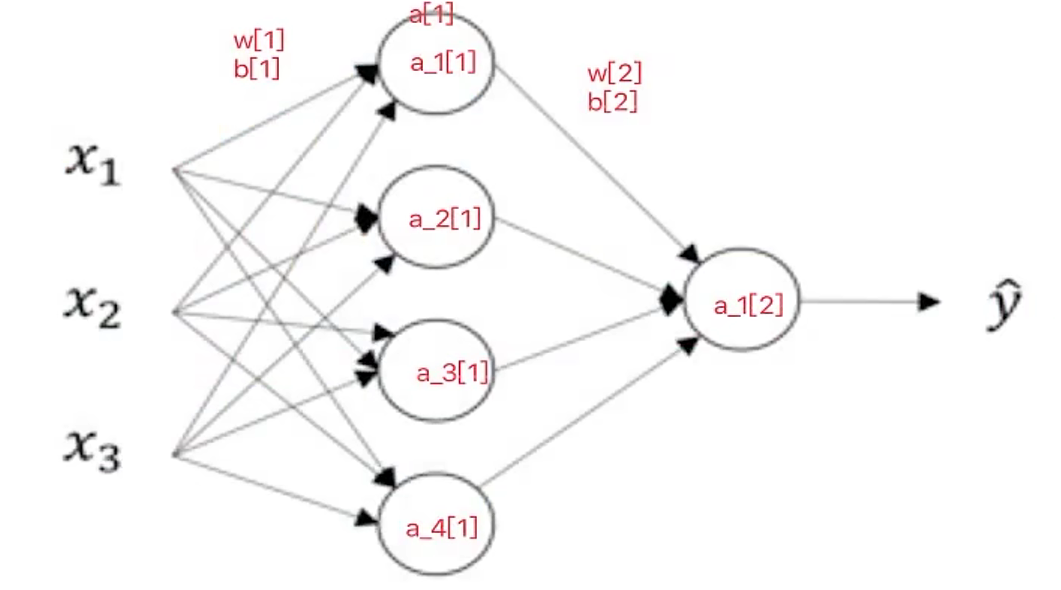
之前已经说过神经网络的结构了,在这不重复叙述。假设我们有如下结构的网络
对于这个网络我们建立一个简单的图示?我们对第一个隐藏层记为[1],输出层为[2]。如下图
计算图如下
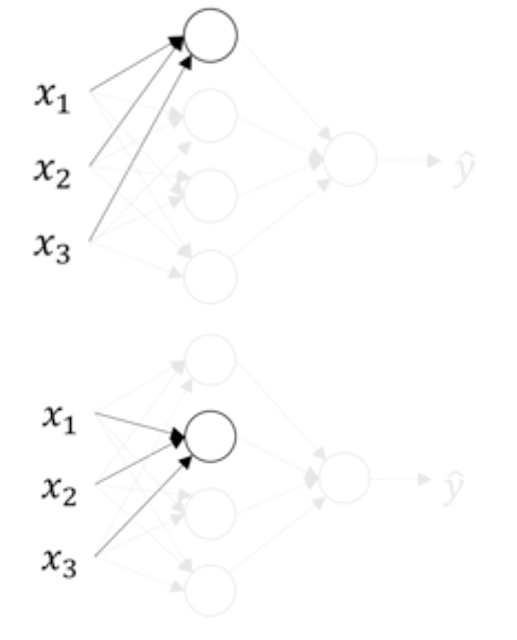
- 每个神经元的计算分解步骤如下
- 第一层中的第一个神经元
- 第一层中的第二个神经元
得出第一层的计算:
1.3.2 单个样本的向量化表示
那么现在把上面的第一层的计算过程过程用更简单的形式表现出来就是这样的计算
那么对于刚才我们所举的例子,将所有层通过向量把整个前向过程表示出来,并且确定每一个组成部分的形状
前向过程计算:
那么如果有多个样本,需要这样去做
- 多个样本的向量化表示
假设一样含有M个样本,那么上述过程变成
1.3.4 激活函数的选择
涉及到网络的优化时候,会有不同的激活函数选择有一个问题是神经网络的隐藏层和输出单元用什么激活函数。之前我们都是选用 sigmoid 函数,但有时其他函数的效果会好得多,大多数通过实践得来,没有很好的解释性。
可供选用的激活函数有:
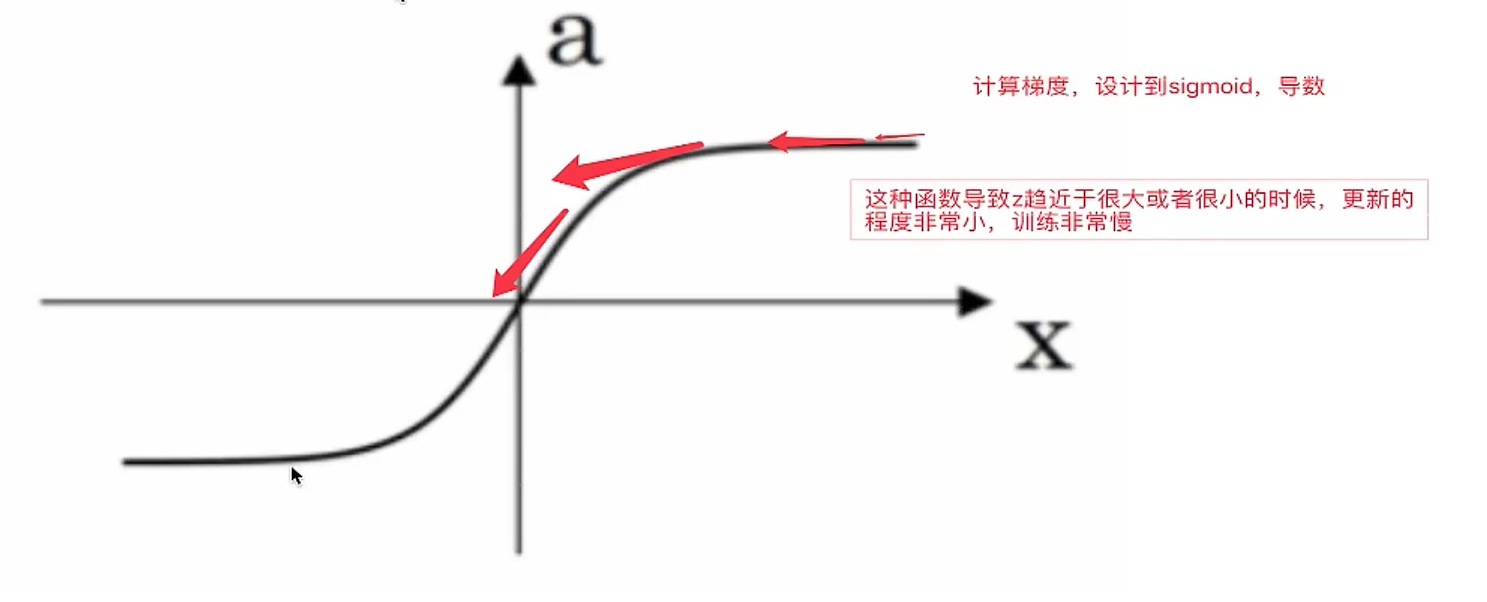
- 1.tanh 函数(the hyperbolic tangent function,双曲正切函数):
效果比 sigmoid 函数好,因为函数输出介于 -1 和 1 之间。
注 :tanh 函数存在和 sigmoid 函数一样的缺点:当 z 趋紧无穷大(或无穷小),导数的梯度(即函数的斜率)就趋紧于 0,这使得梯度算法的速度会减慢。
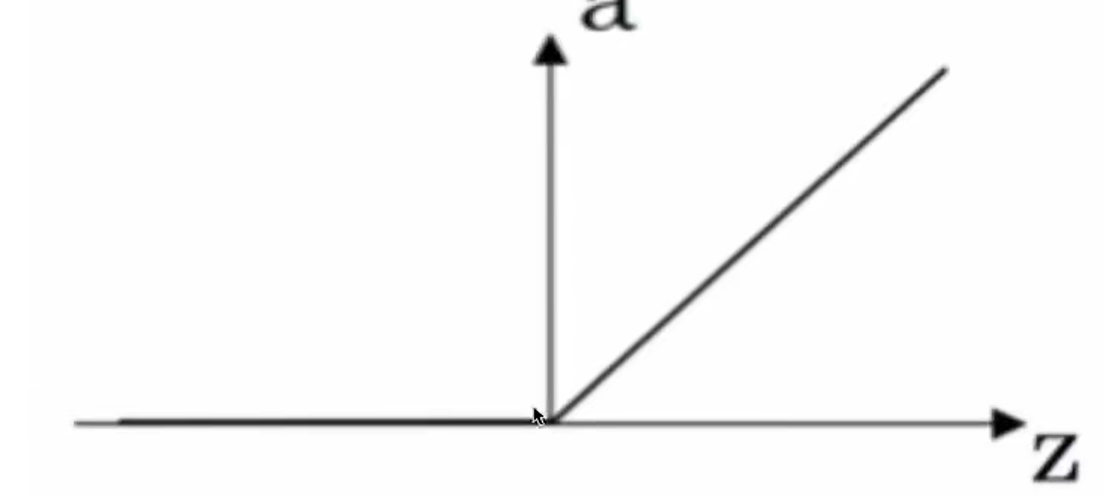
- 2.ReLU 函数(the rectified linear unit,修正线性单元)
当 z > 0 时,梯度始终为 1,从而提高神经网络基于梯度算法的运算速度,收敛速度远大于 sigmoid 和 tanh。然而当 z < 0 时,梯度一直为 0,但是实际的运用中,该缺陷的影响不是很大。
-
Leaky ReLU(带泄漏的 ReLU):
Leaky ReLU 保证在 z < 0 的时候,梯度仍然不为 0。理论上来说,Leaky ReLU 有 ReLU 的所有优点,但在实际操作中没有证明总是好于 ReLU,因此不常用。
1.3.4.1 为什么需要非线性的激活函数
使用线性激活函数和不使用激活函数、直接使用 Logistic 回归没有区别,那么无论神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果相当,就成了最原始的感知器了。
1.3.5 修改激活函数
将上述网络的隐层激活函数修改为tanh,最后一层同样还是二分类,所以激活函数选择依然是sigmoid函数
- 前向传播
- 反向传播梯度下降
那么通过这个计算图来理解这个过程,单个样本的导数推导过程:
1.3.5 练习
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
import sklearn.linear_model
from load_dataset import load_planar_dataset
X, Y = load_planar_dataset()
print ('数据集特征值的形状:', X.shape)
print ('数据集目标值的:', Y.shape)
print ('样本数:', X.shape[1])
def sigmoid(x):
"""
"""
s = 1/(1+np.exp(-x))
return s
* 步骤
* 定义网络结构
* 初始化参数
* 循环一下步骤
* 前向传播
* 计算损失
* 反向传播获得梯度
* 梯度更新
#%% md
### 1、定义神经网络结构
网络输入输出以及隐藏层神经元个数
#%%
def layer_sizes(X, Y):
"""
"""
# 输入层大小2
n_x = X.shape[0]
# 隐层大小
n_h = 4
# 输出层大小
n_y = Y.shape[0]
### END CODE HERE ###
return (n_x, n_h, n_y)
#%% md
### 2、 初始化模型参数
随机初始化权重以及偏置为0
#%%
def initialize_parameters(n_x, n_h, n_y):
"""
输入每层的神经元数量
返回:隐层、输出层的参数
"""
np.random.seed(2)
### 开始
# 创建隐层的两个参数
# 让值小一些
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h, 1))
# 创建输出层前对应的参数
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y, 1))
### 结束
# 检测维度是否符合要求
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
#%% md
### 3、循环中的第一步:前向传播
根据之前给的前向传播公式,完成该函数
使用的函数:np.dot,np.tanh, np.sigmoid
#%%
def forward_propagation(X, parameters):
"""
Argument:
X:(n_feature, m)
Returns:
A2:最后一层的输出
cache:用于反向传播计算的存储中间计算结果的字典
"""
# 获取参数
### 开始
# 取出每一层的参数
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
# 进行一层一层的运算
Z1 = np.matmul(W1, X) + b1
A1 = np.tanh(Z1)
# 第二层
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2)
### 结束
assert(A2.shape == (1, X.shape[1]))
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache
#%% md
### 3、循环中的二步:计算损失
完成损失计算的过程,根据损失公式
设计多个维度,使用np.multiply进行乘法运算
#%%
def compute_cost(A2, Y, parameters):
"""
parameters:最后一层输出,目标值,参数
return:损失
"""
m = Y.shape[1]
### 开始
logpro = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), (np.log(1 - A2)))
cost = - 1 / m * np.sum(logpro)
### 结束
cost = np.squeeze(cost)
assert(isinstance(cost, float))
return cost
#%% md
### 3、循环中的第三步:反向传播
反向传播在这个网络中分为两步
def backward_propagation(parameters, cache, X, Y):
"""
parameters:
cache:存储每层前向传播计算结果
X:数据特征
Y:数据目标值
return:每个参数的梯度
"""
# 得出训练样本数量
m = X.shape[1]
# 获取参数和缓存中的输出
### 开始
W1 = parameters['W1']
W2 = parameters['W2']
A1 = cache['A1']
A2 = cache['A2']
### 结束
# 反向传播计算梯度
### 开始
# 最后一层的参数梯度计算
dZ2 = A2 - Y
dW2 = 1/m * np.dot(dZ2, A1.T)
db2 = 1/m * np.sum(dZ2, axis=1, keepdims=True)
# 隐藏层的参数梯度计算
dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))
dW1 = 1/m * np.dot(dZ1, X.T)
db1 = 1/m * np.sum(dZ1, axis=1, keepdims=True)
### 结束
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads
#%% md
### 3、循环中的第四步:更新梯度
#%%
def update_parameters(parameters, grads, learning_rate = 0.005):
"""
参数:网络参数,梯度,学习率
返回更新之后的参数
"""
# 获取参数以及梯度
### 开始
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
dW1 = grads['dW1']
db1 = grads['db1']
dW2 = grads['dW2']
db2 = grads['db2']
## 结束
# 使用学习率更新参数
### 开始
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
### 结束
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
#%% md
### 4、建立网络模型训练逻辑
#%%
def nn_model(X, Y, num_iterations = 10000, print_cost=False):
"""
"""
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
# 初始化参数
### 开始
# 获取网络的层大小
# 2, 4, 1
n_x, n_h, n_y = layer_sizes(X, Y)
parameters = initialize_parameters(n_x, n_h, n_y)
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
### 结束
# 循环
for i in range(0, num_iterations):
### 开始
# 前向传播
A2, cache = forward_propagation(X, parameters)
# 计算损失
cost = compute_cost(A2, Y, parameters)
# 反向传播计算梯度
grads = backward_propagation(parameters, cache, X, Y)
# 利用梯度更新参数
parameters = update_parameters(parameters, grads)
### 结束
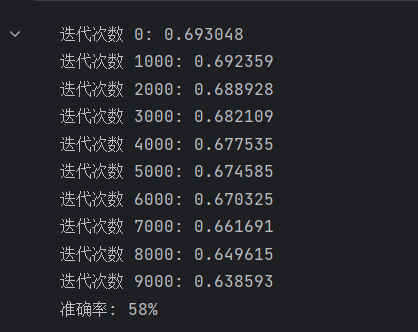
if i % 1000 == 0:
print ("迭代次数 %i: %f" %(i, cost))
return parameters
#%% md
### 5、预测结果
#%%
def predict(parameters, X):
"""
"""
# 计算概率值,以及判断类别
A2, cache = forward_propagation(X, parameters)
predictions = np.array( [1 if x >0.5 else 0 for x in A2.reshape(-1,1)] ).reshape(A2.shape)
return predictions
#%%
# 测试
parameters = nn_model(X, Y, num_iterations = 10000)
predictions = predict(parameters, X)