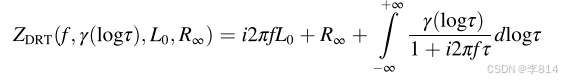使用DNN-DRT对EIS数据进行反卷积(1)
1. 引言
- 电化学阻抗谱(EIS)被广泛用于表征电化学系统。弛豫时间分布 (DRT)是一种强大的非参数替代方法。为了解释电化学阻抗谱数据,通常使用等效电路和物理模型,但等效电路模型(ECM)并不是唯一的,而物理模型实现起来较为困难。弛豫时间分布(DRT)是分析电化学阻抗谱数据的一种替代方法。
- DRT阻抗模型可以用下面的表达式得到,其中L0、R ∞、τ、γ(logτ)分别是电感、欧姆内阻、时间常数和DRT。从中求解γ(logτ)的过程也就称为反卷积。因为受到实验误差和截至频率的影响,从实验数据反卷积求出γ(logτ)仍然具有困难。目前也有很多方法用来反卷积,比如傅里叶变换、遗传算法、Monte Carlo samplers以及岭回归(RR)等方法。
2. 准备工作
2.1 导入相关的库
import os
import numpy as np
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import cvxpy as cp
import sys
from torch import nn
import math
from math import pi, sin, cos, sqrt, log
import compute_DRT
2.2 检查设备,设置标准
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print('Using device:', device)
if device.type == 'cuda':
print(torch.cuda.get_device_name(0))
print('Memory Usage:')
print('Allocated:', round(torch.cuda.memory_allocated(0)/1024**2,3), 'MB')
print('Cached: ', round(torch.cuda.memory_reserved(0)/1024**2,3), 'MB')
np.random.seed(21312)
torch.manual_seed(213912)
os.environ['PYTHONHASHSEED']=str(213912)
plt.rc('text', usetex=True)
plt.rc('font', family='serif', size=15)
plt.rc('xtick', labelsize=15)
plt.rc('ytick', labelsize=15)
3. 人工合成数据
- 这里使用"钩子"模型来合成精确的EIS数据和DRT数据
log_freq_min = -2.
log_freq_max = 6.
N_f = 10*int(log_freq_max-log_freq_min)+1
freq_vec = np.logspace(log_freq_min, log_freq_max, num=N_f, endpoint=True).reshape(N_f,1)
log_tau_min = -log_freq_max
log_tau_max = -log_freq_min
R_inf = 10.
sigma_n = 0.5
// ZARC 1
R_ct_1 = 50.
phi_1 = 0.9
tau_1 = 1E-4
// ZARC 2
R_ct_2 = -10.
phi_2 = 0.9
tau_2 = 1E-1
T_1 = tau_1**phi_1/R_ct_1
T_2 = tau_2**phi_2/R_ct_2
// first DRT
gamma_exact_RR_1 = (R_ct_1)/(2.*pi)*sin((1.-phi_1)*pi)/(np.cosh(phi_1*np.log(tau_vec_RR/tau_1))-cos((1.-phi_1)*pi))
gamma_exact_NN_1 = (R_ct_1)/(2.*pi)*sin((1.-phi_1)*pi)/(np.cosh(phi_1*np.log(tau_vec_NN/tau_1))-cos((1.-phi_1)*pi))
// second DRT
gamma_exact_RR_2 = (R_ct_2)/(2.*pi)*sin((1.-phi_2)*pi)/(np.cosh(phi_2*np.log(tau_vec_RR/tau_2))-cos((1.-phi_2)*pi))
gamma_exact_NN_2 = (R_ct_2)/(2.*pi)*sin((1.-phi_2)*pi)/(np.cosh(phi_2*np.log(tau_vec_NN/tau_2))-cos((1.-phi_2)*pi))
// total gamma
gamma_exact_RR = gamma_exact_RR_1 + gamma_exact_RR_2
gamma_exact_NN = gamma_exact_NN_1 + gamma_exact_NN_2
// normalized gamma
R_ct = R_ct_1 + R_ct_2
gamma_exact_RR_norm = gamma_exact_RR/R_ct
gamma_exact_NN_norm = gamma_exact_NN/R_ct
Z_exact = R_inf + 1./(1./R_ct_1+T_1*(1j*2.*pi*freq_vec)**phi_1) + 1./(1./R_ct_2+T_2*(1j*2.*pi*freq_vec)**phi_2)
Z_exp = Z_exact + sigma_n*(np.random.normal(0, 1, Z_exact.shape) + 1j*np.random.normal(0, 1, Z_exact.shape))
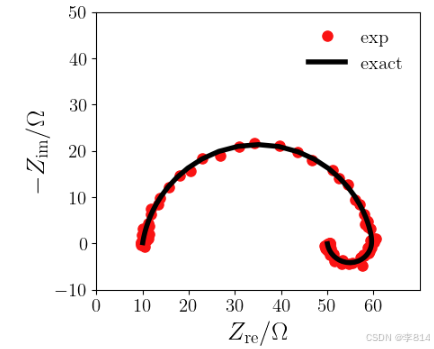
plt.plot(np.real(Z_exp), -np.imag(Z_exp), 'o', markersize=8, color='red', label='exp')
plt.plot(np.real(Z_exact), -np.imag(Z_exact), linewidth=4, color='black', label='exact')
plt.axis([0,70,-10,50])
plt.xticks(np.arange(0, 70, step=10))
plt.legend(frameon=False, fontsize = 15)
plt.gca().set_aspect('equal', adjustable='box')
plt.rcParams['text.latex.preamble'] = r'\usepackage{amsmath}'
plt.xlabel(r'$Z_{\rm re}/\Omega$', fontsize = 20)
plt.ylabel(r'$-Z_{\rm im}/\Omega$', fontsize = 20)
fig = plt.gcf()
fig.set_size_inches(6.472, 4)
plt.show()
运行结果:
"钩子"模型的公式:
4. 岭回归(RR)
- 首先使用RR回归上述合成的数据
// data
Z_RR = np.zeros(2*N_f)
Z_RR[:N_f] = Z_exp.real.flatten()
Z_RR[N_f:] = Z_exp.imag.flatten()
// matrices
A_re_RR = compute_DRT.compute_A_re(freq_vec, tau_vec_RR)
A_im_RR = compute_DRT.compute_A_im(freq_vec, tau_vec_RR)
L2_RR = compute_DRT.compute_L2(log_tau_vec_RR_norm)
L1_RR = compute_DRT.compute_L1(log_tau_vec_RR_norm)
// build matrices for cvxpy
lambda_0 = 1.0E-5
A_R0 = np.zeros((2*N_f,1))
A_R0[0:N_f,0] = 1.0
A_RR = np.hstack( ( A_R0, np.vstack((A_re_RR, A_im_RR)) ) )
L1_RR = np.hstack( ( np.zeros((N_tau_RR-1,1)), L1_RR ) )
Q = A_RR.T@A_RR + lambda_0*L1_RR.T@L1_RR
q = -2.*A_RR.T@Z_RR
// Define and solve the CVXPY problem.
x_RR = cp.Variable(N_tau_RR+1)
prob = cp.Problem(cp.Minimize(cp.quad_form(x_RR, Q) + q.T @ x_RR)) # , [x_RR >= 0]) # we do not need a positive gamma anymore
prob.solve();
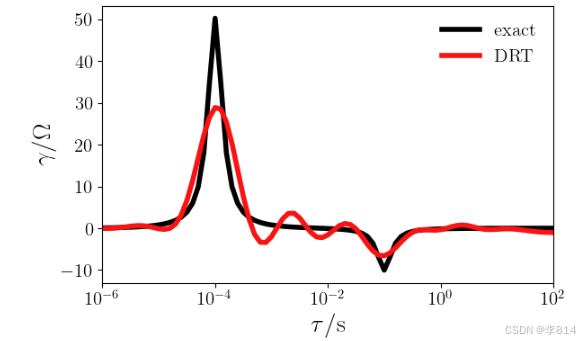
plt.semilogx(tau_vec_RR, gamma_exact_RR, linewidth=4, color='black', label= 'exact')
plt.semilogx(tau_vec_RR, x_RR.value[1:], linewidth=4, color='red', label='DRT')
plt.xlim(1E-6, 1E2)
plt.legend(frameon=False, fontsize = 15)
plt.xlabel(r'$\tau/\rm s$', fontsize=20)
plt.ylabel(r'$\gamma/\Omega$', fontsize=20)
fig = plt.gcf()
fig.set_size_inches(6.472, 4)
plt.show()
运行结果:
具体文献链接: Link
- 用来记录学习过程,具体的可以查看文献了解。