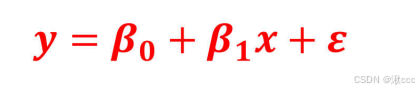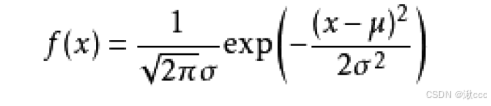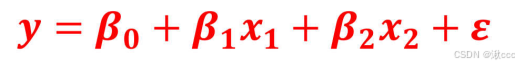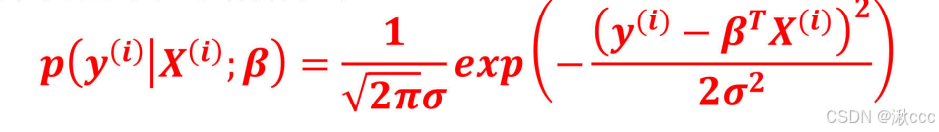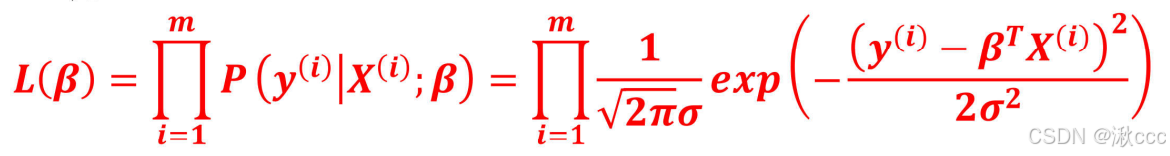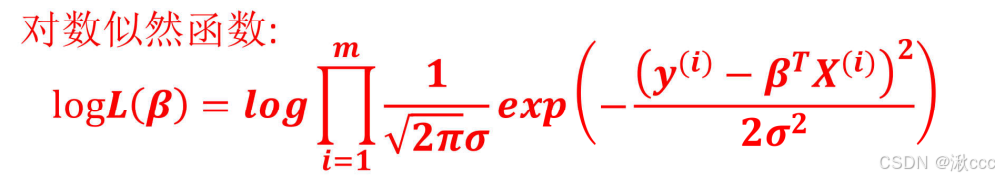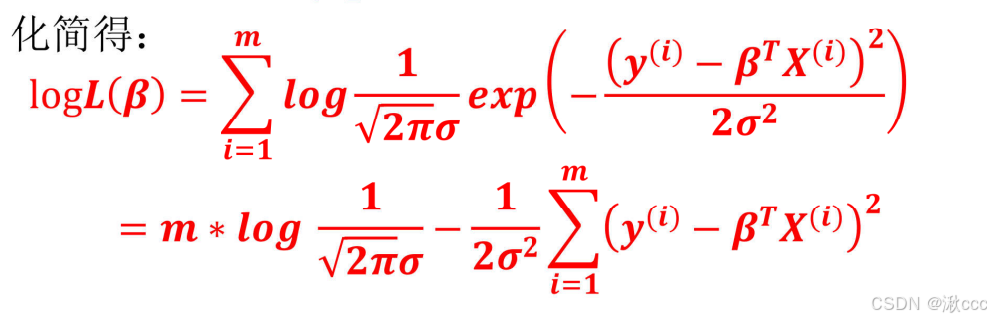目录
一、什么是线性回归
线性回归是利用数理统计中回归分析,来确定两种或多种以上变量间相互依赖的定量关系的一种统计分析方法 。
相关关系:包含因果关系和平行关系
因果关系:回归分析【原因引起结果,需要明确自变量和因变量】
平行关系:相关分析【无因果分析,不区分自变量和因变量】
举例:
| 工资(自变量) | 贷款额度(因变量) |
| 4000 | 10000 |
| 8000 | 12000 |
| 5000 | 8000 |
| 6000 | 15000 |
| 7000 | ? |
工资对贷款额度有多大影响?如何公平的评定工资的影响?
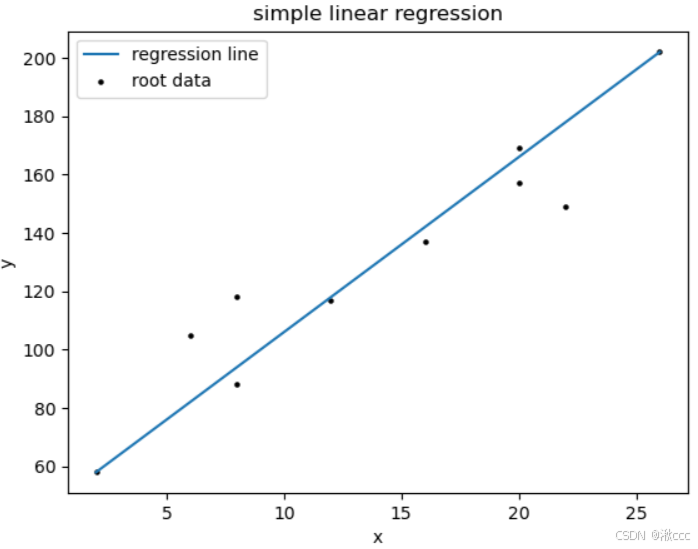
二、一元线性回归模型
一元线性回归模型:

误差项:除线性因素外的随机因素所产生的误差
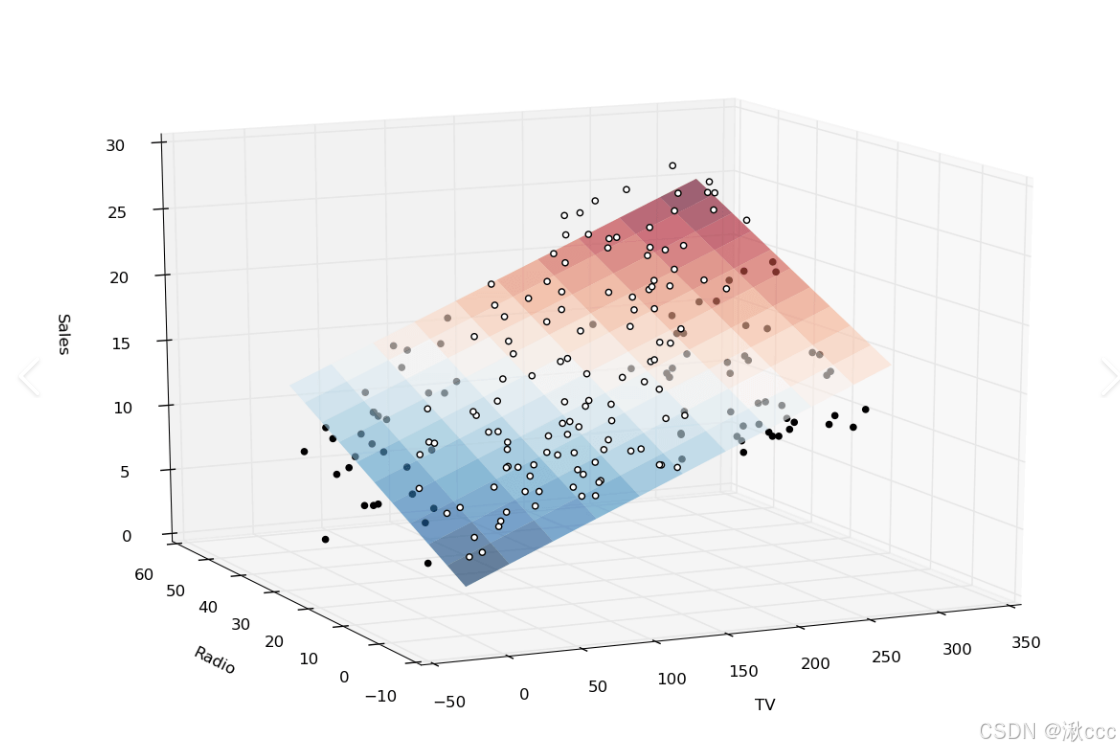
三、多元线性回归模型
多元线性回归模型:
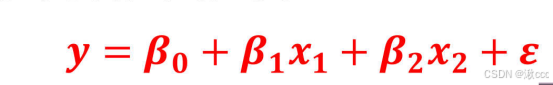

四、误差项分析
1、误差项是否可以忽略
差项不可省略,误差是必然产生的。并且由于产生了误差项,我们便可以基于误差的特点来进行对线性回归的参数估计的。在大多数实际应用中,误差项不可忽略,因为它包含了模型未能解释的随机因素和潜在偏差。
2、误差项的特点
独立同分布
一组随机变量 X1,X2,…,XnX1,X2,…,Xn 是独立同分布的,如果它们既相互独立,又具有相同的概率分布。
- 独立:每个样本点都是独立的
- 同分布:一组随机变量 X1,X2,…,XnX1,X2,…,Xn 是同分布的,如果它们具有相同的概率分布。也就是所有变量的取值规律完全相同。
3、误差项满足高斯分布(正太分布)
(1)、高斯分布公式
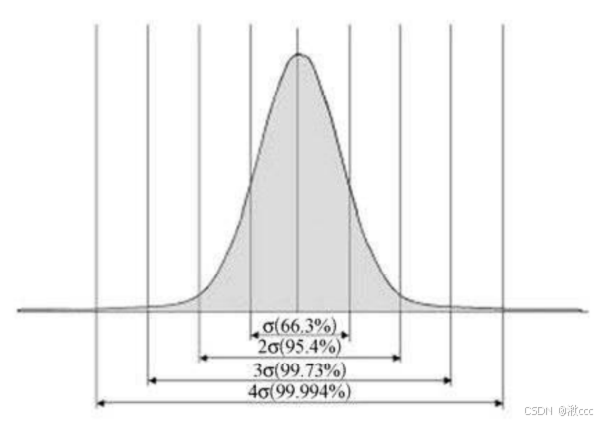
因为误差项满足高斯分布,所以对参数问题的估计就转化成了对误差项的分析。
(2)、公式推导
线性回归公式
转化为矩阵计算
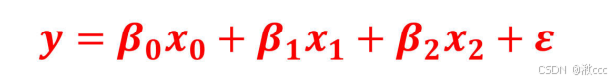
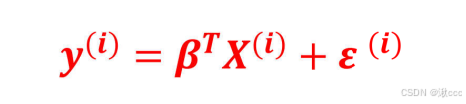
带入高斯分布公式
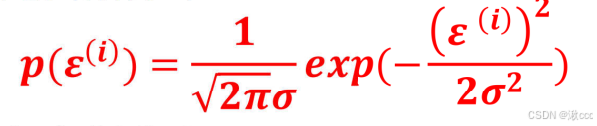
五、极大似然估计
1、什么是极大似然估计
极大似然估计是一种统计方法,用于估计模型参数。其核心思想是:在给定观测数据的情况下,找到最有可能生成这些数据的参数值。
-
假设我们有一个概率模型,其参数为 θθ。
-
给定一组观测数据 X=(x1,x2,…,xn)X=(x1,x2,…,xn),我们希望找到参数 θθ 的值,使得这组数据在该模型下出现的概率最大。
-
换句话说,极大似然估计寻找的是“最合理”的参数值,使得观测数据看起来最“自然”。
2、似然函数求解
取对数
目标函数

使用最小二乘法求解
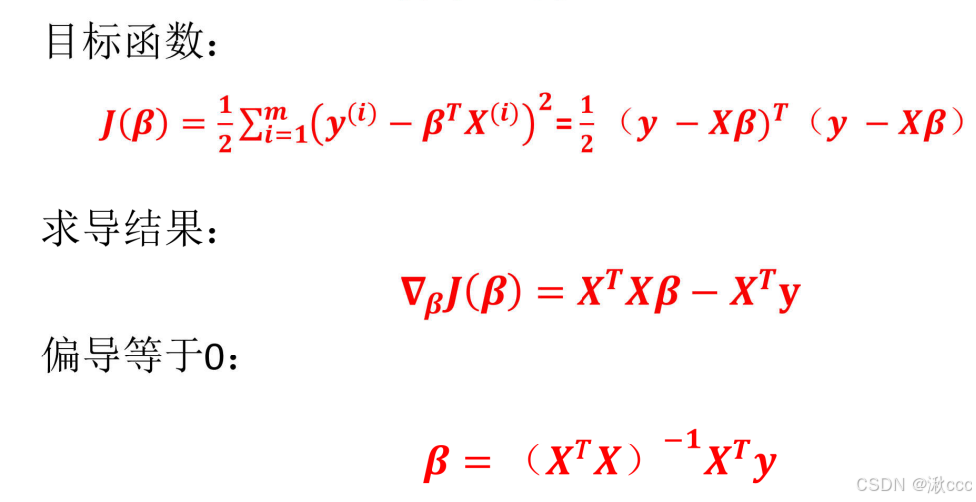
六、模型评估
评估数据以及模型的好坏
1、相关系数
又称皮尔逊相关系数,是研究变量之间相关 关系的度量,一般用字母r表示。

2、拟合优度
即判定系数R方
SSR:回归平方和
SST:离差平方和
1.反映了回归直线的拟合程度。
2.取值范围在[0,1]之间。
3.R方越接近1,说明拟合效果 越好;R方越接近0,说明拟 合效果越差。
4.R方的平方根是相关系数。