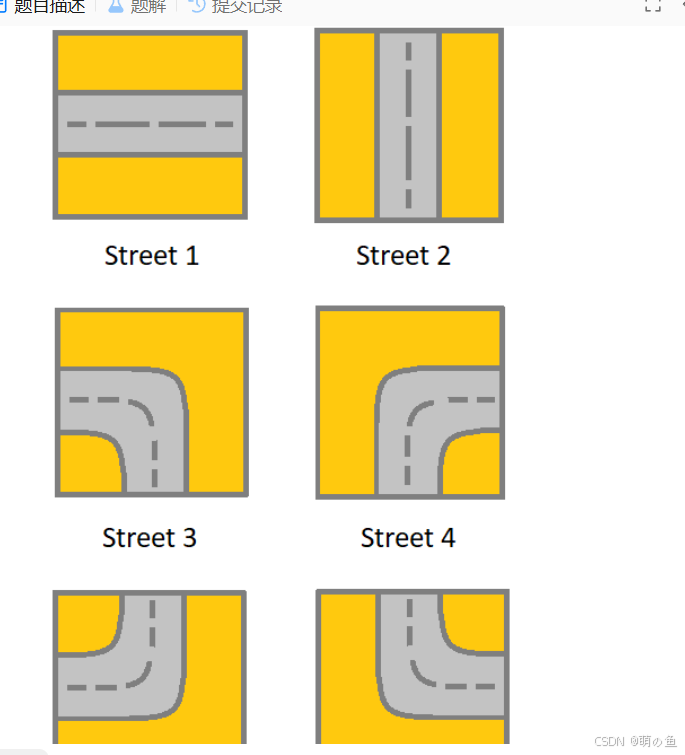
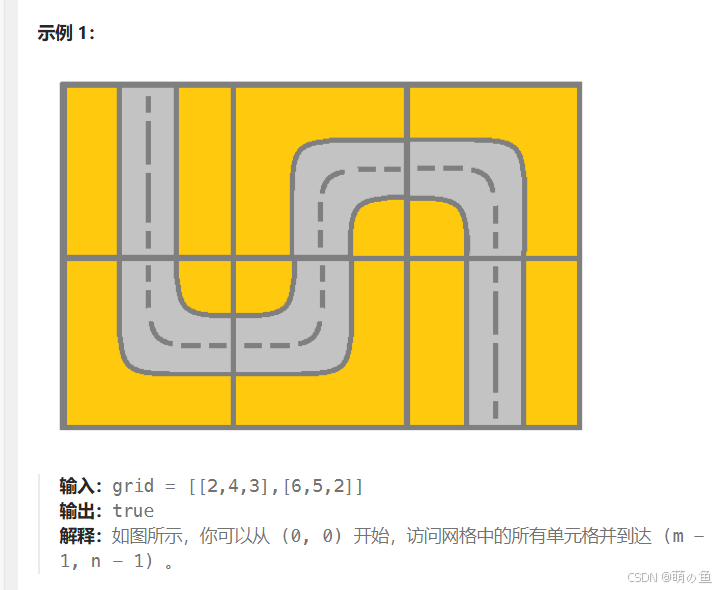
题目如下

数据范围

示例

本题就是加了限制的回溯题，无论是采用bfs或者dfs只需要注意街道与街道的限制（如 在第二种街道想要向下走的时候下面的格子只能是2 3 4类型的街道）只要加了限制条件回溯路径就可以。

通过代码

class Solution {
public:
    bool flag = false;
    int tx, ty;
    bool hasValidPath(vector<vector<int>>& grid) {
        tx = grid.size() - 1;
        ty = grid[0].size() - 1;
        vector<vector<bool>> v(tx + 1, vector<bool>(ty + 1, false));
        dfs(grid, v, 0, 0);
        return flag;
    }
    void dfs(vector<vector<int>>& g, vector<vector<bool>>& v, int x, int y) {
   //     cout << "x=" << x << "y=" << y << "d=" << g[x][y] << endl;
        if (flag)
            return;
        if (x == tx && y == ty) {
            flag = true;
            return;
        }
        v[x][y] = true;
        int d = g[x][y];

        int n = g.size(), m = g[0].size();
        switch (d) {
        case 2: {
            if (x >= 1 && !v[x - 1][y] &&
                (g[x - 1][y] == 3 || g[x - 1][y] == 4 || g[x - 1][y] == 2)) {
                dfs(g, v, x - 1, y);
                v[x - 1][y] = false;
            }
            if (x < n - 1 && !v[x + 1][y] &&
                (g[x + 1][y] == 6 || g[x + 1][y] == 5 || g[x + 1][y] == 2)) {
                dfs(g, v, x + 1, y);
                v[x + 1][y] = false;
            }
            break;
        }
        case 1: {
            if (y >= 1 && !v[x][y - 1] &&
                (g[x][y - 1] == 6 || g[x][y - 1] == 4 || g[x][y - 1] == 1)) {
                dfs(g, v, x, y - 1);
                v[x][y - 1] = false;
            }
            if (y < m - 1 && !v[x][y + 1] &&
                (g[x][y + 1] == 3 || g[x][y + 1] == 5 || g[x][y + 1] == 1)) {
                dfs(g, v, x, y + 1);
                v[x][y + 1] = false;
            }
            break;
        }
        case 3: {
            if (y < m - 1 && !v[x][y + 1] &&
                (g[x][y + 1] == 1 || g[x][y + 1] == 4 || g[x][y + 1] == 6)) {
                dfs(g, v, x, y + 1);
                v[x][y + 1] = false;
            }
            if (x < n - 1 && !v[x + 1][y] &&
                (g[x + 1][y] == 5 || g[x + 1][y] == 6 || g[x + 1][y] == 2)) {
                dfs(g, v, x + 1, y);
                v[x + 1][y] = false;
            }
            break;
        }
        case 4: {
            if (y < m - 1 && !v[x][y + 1] &&
                (g[x][y + 1] == 3 || g[x][y + 1] == 1 || g[x][y + 1] == 5)) {
                dfs(g, v, x, y + 1);
                v[x][y + 1] = false;
            }
            if (x < n - 1 && !v[x + 1][y] &&
                (g[x + 1][y] == 2 || g[x + 1][y] == 5 || g[x + 1][y] == 6)) {
                dfs(g, v, x + 1, y);
                v[x + 1][y] = false;
            }
            break;
        }
        case 5: {
            if (x >= 1 && !v[x - 1][y] &&
                (g[x - 1][y] == 3 || g[x - 1][y] == 4 || g[x - 1][y] == 2)) {
                dfs(g, v, x - 1, y);
                v[x - 1][y] = false;
            }
            if (y >= 1 && !v[x][y - 1] &&
                (g[x][y - 1] == 1 || g[x][y - 1] == 4 || g[x][y - 1] == 6)) {
                dfs(g, v, x, y - 1);
                v[x][y - 1] = false;
            }
            break;
        }
        case 6: {
            if (x >= 1 && !v[x - 1][y] &&
                (g[x - 1][y] == 3 || g[x - 1][y] == 4 || g[x - 1][y] == 2)) {
                dfs(g, v, x - 1, y);
                v[x - 1][y] = false;
            }
            if (y < n - 1 && !v[x][y + 1] &&
                (g[x][y + 1] == 3 || g[x][y + 1] == 1 || g[x][y + 1] == 5)) {
                dfs(g, v, x, y + 1);
                v[x][y + 1] = false;
            }
            break;
        }
        }
    }
};