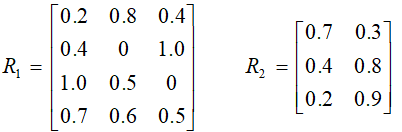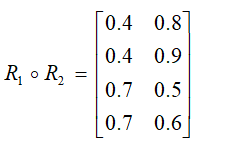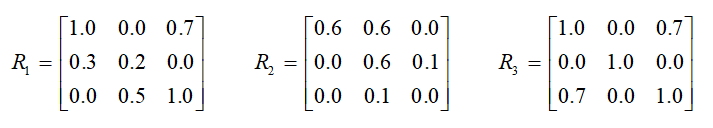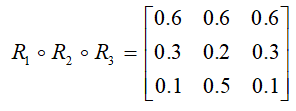目录
人工智能之盲目搜索算法
第1关:盲目搜索之宽度优先搜索算法
# -*- coding:utf-8 -*-
class Maze:
def __init__(self, map, n, m, x, y):
self.ans = 0 #最短步长结果
self.map = map #迷宫地图map[0,n-1][0,m-1](下标0开始)
self.n = n #迷宫地图行数n
self.m = m #迷宫地图列数m
self.x = x #起点,行坐标(下标0开始)
self.y = y #起点,列坐标(下标0开始)
class Solution:
def solveMaze(self, maze):
"""求解迷宫问题
:type: maze: class Maze #迷宫的数据结构类
:rtype: maze.ans: int #返回最短路径长度
"""
#请在这里补充代码,完成本关任务
#********** Begin **********#
maze.ans = 0
que = [(maze.x, maze.y, maze.ans)] #宽度搜索-队列(列表类型)
vis = {(maze.x, maze.y):True} # 访问标记-字典类型
dir = [[0, -1],[0, 1],[-1, 0],[1, 0]] # 移动方向控制
while que.__len__()>0:
node = que[0] # 出队
del que[0]
x = node[0]
y = node[1]
ans = node[2]
if x==0 or x==maze.n-1 or y==0 or y==maze.m-1: # 边界,出迷宫,更新结果
if maze.ans==0 or maze.ans>ans:
maze.ans =ans
for i in range(4): #上下左右移动
newx = x + dir[i][0] # 新的行坐标
newy = y + dir[i][1] #新的列坐标
if 0<=newx and newx<maze.n and 0<=newy and newy<maze.m \
and maze.map[newx][newy]==1 and (newx, newy) not in vis:
vis[(newx,newy)] = True
que.append((newx, newy, ans+1)) #入队
return maze.ans # 返回结果
#********** End **********#
第2关:盲目搜索之深度优先搜索算法
# -*- coding:utf-8 -*-
class Solution:
def __init__(self, n=0):
self.vis = [[]] #用于标记是否存在皇后的二维列表(初始值全为0)
self.ans = 0 #用于存储答案(N皇后方案数,初始值0)
self.n = n #用于存储皇后数量n
def solveNQueens(self):
"""求解N皇后问题(调用self.DFS函数)
:rtype: self.ans: int #返回N皇后放置方案数
"""
#请在这里补充代码,完成本关任务
#********** Begin **********#
self.vis = [[0 for j in range(50)] for i in range(3)]
self.ans = 0
self.DFS(1, self.n)
return self.ans
#********** End **********#
def DFS(self, row, n):
"""深度优先搜索N皇后问题的解空间
:type: row: int #NxN棋盘的第row行
:type: n: int #皇后数量n
:rtype: None #无返回值
"""
#请在这里补充代码,完成本关任务
#********** Begin **********#
if row == n+1:
self.ans += 1
return
for i in range(1,n+1,1):
if self.vis[0][row-i+n]==0 and self.vis[1][i] == 0 and self.vis[2][row+i]==0 :
self.vis[0][row-i+n] = self.vis[1][i] = self.vis[2][row+i] = 1
self.DFS(row+1, n)
self.vis[0][row-i+n] = self.vis[1][i] = self.vis[2][row+i] = 0
#********** End **********#问题求解的基本原理
第1关:状态空间法问题求解
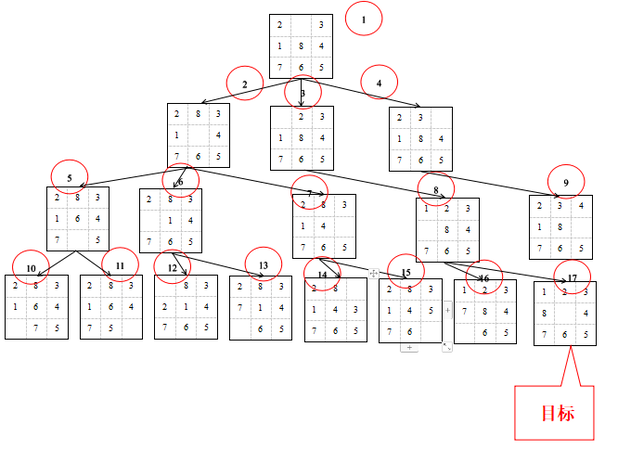
1、给出一组八数码问题的状态空间和目标状态:
下列哪一个路径是该问题的解路径( )
A、1->3->8->17
2、下列说法正确的是( )
A、常用的搜索策略方式为盲目搜索与启发式搜索。
B、A*算法属于启发式搜索。
C、广度优先搜索算法属于盲目搜索。
3、在求解问题时,启发式搜索算法一定比盲目搜索算法好。
B、错
第2关:问题归约法问题求解
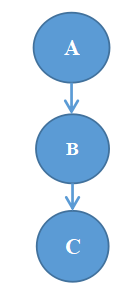
1、如图是一个问题的与或树,如果 C 无解, A 可能有解。
与或树
B、错
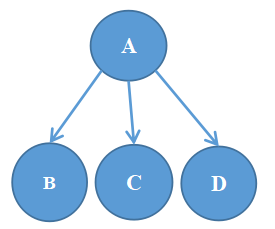
2、如图是某个问题的与或树,下列说法正确的是( )
与或树
B、如果 A 有解,则 B 、C 、D 一定有一个结点有解。
C、如果 B 、C 、D 都有解,则 A 一定有解。
D、如果 B 、C 、D 都无解,则 A 一定无解。
3、如图是某个问题的与或树,下列说法正确的是( )
与或树
A、如果 A 有解,则 B 、C 、D 一定都有解。
C、如果 B 、C 、D 都有解,则 A 一定有解。
D、如果 B 有解,C 、D 无解,则 A 一定无解。
启发式搜索算法
第1关:评估函数和启发信息
1、评估函数的作用就是估计待扩展结点在问题求解中的价值。
A、对
2、启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到目标。
A、对
第2关:A*搜索算法
class Array2D:
"""
说明:
1.构造方法需要两个参数,即二维数组的宽和高
2.成员变量w和h是二维数组的宽和高
3.使用:‘对象[x][y]’可以直接取到相应的值
4.数组的默认值都是0
"""
def __init__(self, w, h):
self.w = w
self.h = h
self.data = []
self.data = [[0 for y in range(h)] for x in range(w)]
def showArray2D(self):
for y in range(self.h):
for x in range(self.w):
print(self.data[x][y], end=' ')
print("")
def __getitem__(self, item):
return self.data[item]
class Point:
"""
表示一个点
"""
def __init__(self, x, y):
self.x = x
self.y = y
def __eq__(self, other):
if self.x == other.x and self.y == other.y:
return True
return False
def __str__(self):
return "x:" + str(self.x) + ",y:" + str(self.y)
class AStar:
"""
AStar算法的Python3.x实现
"""
class Node: # 描述AStar算法中的节点数据
def __init__(self, point, endPoint, g=0):
self.point = point # 自己的坐标
self.father = None # 父节点
self.endPoint = endPoint
self.g = g # g值,g值在用到的时候会重新算
self.h = (abs(endPoint.x - point.x) + abs(endPoint.y - point.y)) * 10 # 计算h值
def __init__(self, map2d, startPoint, endPoint, passTag=0):
"""
构造AStar算法的启动条件
:param map2d: Array2D类型的寻路数组
:param startPoint: Point或二元组类型的寻路起点
:param endPoint: Point或二元组类型的寻路终点
:param passTag: int类型的可行走标记(若地图数据!=passTag即为障碍)
"""
# 开启表
self.openList = []
# 关闭表
self.closeList = []
# 寻路地图
self.map2d = map2d
# 起点终点
# ********** Begin **********#
self.startPoint = startPoint
self.endPoint = endPoint
# ********** End **********#
# 可行走标记
self.passTag = passTag
def getMinNode(self):
"""
获得openlist中F值最小的节点
:return: Node
"""
# ********** Begin **********#
nowf = self.openList[0]
minf=self.openList[0].g +self.openList[0].h
for i in self.openList:
if minf > i.g + i.h:
minf = i.g + i.h
nowf = i
return nowf
# ********** End **********#
def pointInCloseList(self, point):
for node in self.closeList:
if node.point == point:
return True
return False
def pointInOpenList(self, point):
for node in self.openList:
if node.point == point:
return node
return None
def endPointInCloseList(self):
for node in self.openList:
if node.point == self.endPoint:
return node
return None
def searchNear(self, minF, offsetX, offsetY):
"""
搜索节点周围的点
:param minF:F值最小的节点
:param offsetX:坐标偏移量
:param offsetY:
:return:
"""
# 越界检测
# ********** Begin **********#
if minF.point.x + offsetX >= self.map2d.w or minF.point.y + offsetY >= self.map2d.h or minF.point.x + offsetX < 0 or minF.point.y + offsetY < 0:
return
# ********** End **********#
# 如果是障碍,就忽略
if self.map2d[minF.point.x + offsetX][minF.point.y + offsetY] != self.passTag:
return
# 如果在关闭表中,就忽略
currentPoint = Point(minF.point.x + offsetX, minF.point.y + offsetY)
currentNode = AStar.Node(currentPoint,self.endPoint)
if self.pointInCloseList(currentPoint):
return
# 设置单位花费
if offsetX == 0 or offsetY == 0:
step = 10
else:
step = 14
# 如果不再openList中,就把它加入openlist
# ********** Begin **********#
if not self.pointInOpenList(currentPoint):
# print(currentNode.g)
currentNode.g = step + minF.g
# print(currentNode)
currentNode.father = minF
self.openList.append(currentNode)
# ********** End **********#
# 如果在openList中,判断minF到当前点的G是否更小
if minF.g + step < currentNode.g: # 如果更小,就重新计算g值,并且改变father
currentNode.g = minF.g + step
currentNode.father = minF
def start(self):
"""
开始寻路
:return: None或Point列表(路径)
"""
# 判断寻路终点是否是障碍
if self.map2d[self.endPoint.x][self.endPoint.y] != self.passTag:
return None
# 1.将起点放入开启列表
startNode = AStar.Node(self.startPoint, self.endPoint)
self.openList.append(startNode)
# 2.主循环逻辑
while True:
# 找到F值最小的点
minF = self.getMinNode()
# 把这个点加入closeList中,并且在openList中删除它
self.closeList.append(minF)
self.openList.remove(minF)
# 判断这个节点的上下左右节点
# ********** Begin **********#
self.searchNear(minF,0,-1)
self.searchNear(minF,1,0)
self.searchNear(minF,-1,0)
self.searchNear(minF,0,1)
# ********** End **********#
# 判断是否终止
point = self.endPointInCloseList()
if point: # 如果终点在关闭表中,就返回结果
# print("关闭表中")
cPoint = point
pathList = []
while True:
if cPoint.father:
pathList.append(cPoint.point)
cPoint = cPoint.father
else:
return list(reversed(pathList))
if len(self.openList) == 0:
return None语义网络
第1关:语义网络
1、下列关于语义网络的结构方式描述正确的是?
A、语义网络是一种用图来表示知识的结构化方式。
B、语义网络是一种面向语义的结构,它们一般使用一组推理规则,规则是为了正确处理出现在网络中的特种弧而专门设计的。
C、语义网络的一个重要特性是属性继承。
D、在属性继承的基础上可以方便地进行推理是语义网络的优点之一。
2、下列关于语义网络的特点阐述错误的是?
D、可利用语义网络的结构关系检索和推理,效率高。
3、对于语义网络概念的描述错误的是?
D、作为知识表示的一种形式,语义网络对计算机程序员和AI研究人员大有用途,尤其是在集合成员关系和精度这两个元素。
4、下列关于语义网络表示法的特点说法正确的是?
A、语义网络表示法的结构性好。
B、语义网络表示法的下层结点可以继承、新增和变异上层结点的属性,从而实现信息共享。
D、语义网络的表达范围有限,一旦结点个数太多,网络结构复杂,推理就难以进行。
不确定性推理
第1关:可信度方法
1、如果证据 E 的出现使得结论 H 一定程度为真,则可信度因子( )
C、0 < CF( H , E ) < 1
2、在可信度方法中,若证据 A 的可信度 CF(F)=0,这意味着( )
A、对证据 A 一无所知
3、设有如下一组推理规则:
r 1: IF E1 THEN E2 (0.6)
r 2: IF E2 AND E3 THEN E4 (0.8)
r 3: IF E4 THEN H (0.7)
r 4: IF E5 THEN H (0.9)
且已知CF(E1)=0.5,CF(E3)=0.6,CF(E 5)=0.4,结论H的初始可信度一无所知,则CF(H)=( )
D、0.47
第2关:证据理论
1、在证据理论中,信任函数与似然函数对(Bel(A),Pl(A))的值为(0,0)时,表示( )
D、A 为假
2、基本概率分配函数之值是概率。
B、错
3、设样本空间D=a,b,c,d,M 1、M2为定义在2 D上的概率分配函数:M1:M1(b,c,d)=0.7,M 1(a,b,c,d)=0.3,M 1的其余基本函数均为0
M 2:M 2(a,b)=0.6,M 2(a,b,c,d)=0.4,M 的其余基本函数均为0
则,它们的正交和M=M1⊕M2=( )
A、0
第3关:模糊推理基础
1、设有论域U=x 1,x 2,x 3,x 4,x 5,A、B是U上的两个模糊集,且有
A=0.85/x 1+0.7/x 2+0.9/x 3+0.9/x 4+0.7/x 5
B=0.5/x 1+0.65/x 2+0.8/x 3+0.98/x 4+0.77/x 5
则A∩B=
A、0.5/x1+0.65/x2+0.8/x3+0.9/x4+0.7/x5
2、设有论域U=x 1,x 2,x 3,x 4,x 5,A、B是U上的两个模糊集,且有
A=0.85/x 1+0.7/x 2+0.9/x 3+0.9/x 4+0.7/x 5
B=0.5/x 1+0.65/x 2+0.8/x 3+0.98/x 4+0.77/x 5
则A∪B=
B、0.85/x1+0.7/x2+0.9/x3+0.98/x4+0.77/x5
3、设有论域U=x 1,x 2,x 3,x 4,x 5,A、B是U上的两个模糊集,且有
A=0.85/x 1+0.7/x 2+0.9/x 3+0.9/x 4+0.7/x 5
B=0.5/x 1+0.65/x 2+0.8/x 3+0.98/x 4+0.77/x 5
则¬A=
C、0.15/x1+0.3/x2+0.1/x3+0.1/x4+0.3/x5
4、设有如下两个模糊关系:
则:
A、对
5、设有如下两个模糊关系:
则:
B、对
第4关:模糊推理及其应用
OIL=100.0#定义油渍论域
Stain=100.0#定义污渍论域
def ruleMD(stain):
if stain<0 or stain>100:
return 0.0
else:#当传入的参数在0-100之间时,该处有两种情况
# 计算MD的结果,并且和同参数下的SD结果相比较,得出一个结果
if stain>=0 and stain<=50:
return stain/50.0
else:
# 同上的操作,得出结果和同参数下的LD相比较
return (100-stain)/50.0
def ruleSD(stain):
#SD部分的rule
#当输入的参数0 <= x <= 50, 执行该方法
result=(50-stain)/50.0
returnMDresult=ruleMD(stain)
#传参数到MD中,计算,并比较
#1、相同,则返回结果为SD,2、SD的结果大,则返回SD,3、MD的结果大,则返回MD的返回值
if result<returnMDresult:
return 2.0
else:
return 1.0
def ruleLD(stain):
# LD部分的rule
# 当输入的参数在50 - 100之间时,执行
result = (stain - 50) / 50
returnMDresult = ruleMD(stain)
# 同时将参数传入给MD,同时比较MD方法传回来的参数和该方法求出的值相比较,求出最后的最适合的预测值
# ********** Begin **********#
if result < returnMDresult:
return 2.0
else:
return 3.0
# ********** End **********#
def ruleMG(oil):
#当传入的参数在0 - 100之间时,该处有两种情况
if oil<0 or oil>100:
return 0#当在论域之外时,直接返回无结果
else:
if oil>=0 and oil<=50:
return oil/50.0#计算MD的结果,并且和同参数下的SD结果相比较,得出一个结果
else:
return (100 - oil) / 50#同上的操作,得出结果和同参数下的LD相比较
def ruleSG(oil):
if oil<0 or oil>50:
return 0.0
else:
#SG部分的rule
#当输入的参数0<=x<=50,执行该方法
result=(50-oil)/50.0
returnMGresult=ruleMG(oil)
#传参数到MD中,计算,并比较
#1、相同,则返回结果为SD,2、SD的结果大,则返回SD,3、MD的结果大,则返回MD的返回值
if result<returnMGresult:
return 2.0
else:
return 1.0
def ruleLG(oil):
# LD部分的rula
#当输入的参数在50 - 100之间时,执行
#同时将参数传入给MG,同时比较MG方法传回来的参数和该方法求出的值相比较,求出最后的最适合的预测值
returnMGresult=ruleMG(oil)
result=(oil-50)/50.0
#比较后,得到预测值
if result<returnMGresult:
return 2.0
else:
return 3.0
#F函数,总的函数,从该函数中分流到rule的三个函数中
def Function(oil,stain):
#VS: SD, SG
#S: MD, SG
#M: SD, MG MD, MG LD, SG
#L: SD, LG MD,LG LD,MG
#XL: LD, LG
#根据规则输出最后的洗涤时间
#需要客户的正确输入
# ********** Begin **********#
if stain >= 0 and stain <= 50:
result_D = ruleSD(stain)
else:
result_D = ruleLD(stain)
if oil >= 0 and oil <= 50:
result_G = ruleSG(oil)
else:
result_G = ruleLG(oil)
# ********** End **********#
#比较最后的结果,返回结果控制规则表,例如VS在表格中的坐标是(1,1),S的坐标是(2,1)
if result_D==1.0 and result_G==1.0:
return 1 #return VS
elif result_G==1.0 and result_D==2.0:
return 2 #return S
elif (result_D==1.0 and result_G==2.0) or (result_G==2.0 and result_D==2.0) or (result_G==1.0 and result_D==3.0):
return 3 #reutrn M
elif (result_D==1.0 and result_G==3.0) or (result_D==2.0 and result_G==3.0) or (result_D==3.0 and result_G==2.0):
return 4 #return L
elif result_G==3.0 and result_D==3.0:
return 5 #return VL
概率理论和不确定性
第1关:概率理论和不确定性
1、下列对概率论原理描述正确的是?
A、概率论,是研究随机现象数量规律的数学分支。
B、随机现象是相对于决定性现象而言的,在一定条件下必然发生某一结果的现象称为决定性现象。
C、随机现象则是指在基本条件不变的情况下,每一次试验或观察前,不能肯定会出现哪种结果,呈现出偶然性。
D、事件的概率是衡量该事件发生的可能性的量度。
2、下列选项对概率论的定义描述正确的是?
A、传统概率又称为拉普拉斯概率,因为其定义是由法国数学家拉普拉斯提出的。如果一个随机试验所包含的单位事件是有限的,且每个单位事件发生的可能性均相等,则这个随机试验叫做拉普拉斯试验。
B、传统概率在实践中被广泛应用于确定事件的概率值。
D、传统概率的理论依据是:如果没有足够的论据来证明一个事件的概率大于另一个事件的概率,那么可以认为这两个事件的概率值相等。
3、“因为事件在一定程度上是以集合的含义定义的,因此可以把集合计算方法直接应用于事件的计算,也就是说,在计算过程中,可以把事件当作集合来对待。”这句话是否是正确的?
A、正确
4、下列关于概率理论和不确定性的描述正确的是?
A、概率理论在处理不确定性方面起着重要的作用。
B、概率理论在处理不确定性方面有一个障碍,就是大多数人在评估风险时都是主观的(而不是分析性的)。
C、我们经常用贝叶斯网络来应对不确定性。
D、对概率理论进行任何讨论的起点都是从执行某个过程的实验开始过程。
确定性推理
第1关:推理概述
1、人们在对各种事物进行分析、综合并最后做出决定时,通常是从已知的事实出发,通过运用已掌握的知识,找出其中蕴含的事实,或归纳出新的事实。这一过程通常称为推理,即从初始证据出发,按某种策略不断运用知识库中的已有知识,逐步推出结论的过程称为推理。( )
A、对
2、下列有关推理的说法错误的是( )
D、已知事实是使推理得以向前推进,并逐步达到最终目的的依据。
3、若按推出结论的途径来分,推理可分为( )
A、演绎推理
B、归纳推理
C、默认推理
4、下列有关推理的分类正确的是( )
A、按照推理过程中推出的结论是否越来越接近最终目标来划分,可分为单调推理与非单调推理。
B、归纳推理是从个别到一般的过程,是从足够多的具体事例中归纳出一般性知识的推理过程。
C、在单调推理中,随着推理向前推进及新知识的加入,推出的结论越来越接近最终目标。
D、如果推理过程中运用与推理有关的启发性知识,则称为启发式推理,否则称为非启发式推理。
5、下列有关推理方向说法正确的是( )
C、把正向推理和逆向推理结合起来所进行的推理称为混合推理。
6、下面哪些是常见的冲突消解策略( )
A、按针对性排序。
B、按已知事实的新鲜性排序。
C、按匹配度排序。
D、按条件个数排序。
第2关:自然演绎推理
1、下列说法正确的是( )
C、原子谓词公式是一个不能再分解的命题。
2、将下列谓词公式转化为字句集:
(∀x){[﹁P(x)∨﹁Q(x)]→(∃y)[S(x,y)∧Q(x)]}∧(∀x)[P(x)∨B(x)]
下列步骤中哪些是错误的( )
F、化为 Skolem 标准形: ( ∀ x )( ∀ w ){ Q ( x ) ∧ [ P ( x ) ∨ S ( x ,f ( x ) ) ∧Q ( x ) ] ∧ [ P ( w ) ∨ B ( w ) ]
第3关:鲁宾孙归结原理
1、谓词公式不可满足的充要条件是其字句集不可满足。( )
A、对
2、为了要证明字句集S的不可满足性,只要对其中可进行字句进行归结,并把归结式加入字句集S,或者用归结式替换它的亲本字句,然后对新字句集(S 1或S 2)证明不可满足性就可以了。( )
A、对
3、设C 1=¬P∨Q∨R,C 2=¬Q∨S,L 1=Q,L 2=¬Q,通过归结方法可得C 12=¬P∨R∨S
A、对
第4关:归结反演
S = [] # 以列表形式存储子句集S
""" 读取子句集文件中子句,并存放在S列表中 - 每个子句也是以列表形式存储 - 以析取式分割 - 例如:~p ∨ ~q ∨ r 存储形式为 ['~p', '~q', 'r'] """
def readClauseSet(filePath):
global S
for line in open(filePath, mode='r', encoding='utf-8'):
line = line.replace(' ', '').strip()
line = line.split('∨')
S.append(line)
""" - 为正文字,则返回其负文字 - 为负文字,则返回其正文字 """
def opposite(clause):
if '~' in clause:
return clause.replace('~', '')
else:
return '~' + clause
""" 归结 """
def resolution():
global S
end = False
while True:
if end: break
father = S.pop()
for i in father[:]:
if end: break
for mother in S[:]:
if end: break
j = list(filter(lambda x: x == opposite(i), mother))
if j == []:
continue
else:
print('\n亲本子句:' + ' ∨ '.join(father) + ' 和 ' + ' ∨ '.join(mother))
father.remove(i)
mother.remove(j[0])
#********** Begin **********#
if(father == [] and mother == []):
print('归结式:NIL')
end = True
elif father == []:
print('归结式:' + ' ∨ '.join(mother))
elif mother == []:
print('归结式:' + ' ∨ '.join(mother))
else:
print('归结式:' + ' ∨ '.join(father))
#********** End **********#常用的知识表示方法
第1关:知识表示方法
1、“表示方法可以分为替代表示法和直接表示法两类”判断这句话是否正确?
A、正确
2、下列对直接表示法描述正确的是?
A、直接表示法是Gelernter在1963年提出的。用于基于传统欧氏几何证明的几何定理证明器。
B、计算机对直接表示的信息难以处理是导致直接表示没有得到长足发展的原因。
C、直接表示难以表示定量信息。
D、直接表示不能描述自然世界的全部信息。
3、下列对谓词和命题的对比说法正确的是?
A、谓词的表达能力强。
B、谓词可以代表变化的情况。
D、谓词可以在不同的知识之间建立联系。
4、下列对谓词逻辑法的描述错误的是?
D、谓词逻辑法的局限性,没有扎实的数学基础。
5、下列对产生式规则表示法描述正确的是?
A、产生式规则表示法的推理方法有正向推理,反向推理,双向推理。
B、产生式规则表示法的优点有:模块性,灵活性,自然性,透明性。
C、产生式规则表示法的缺点有:知识库维护难, 效率低, 理解难。
D、产生式系统的基本特征有:数据库和一个解释程序。
知识的定义
第1关:知识与知识表示的定义
1、下列说法正确的是?
B、如果打雷,那么就很可能下雨。这是一条知识。
C、知识以各种形式储存在计算机中。
D、将有关信息关联在一起所形成的信息结构称为知识。
知识表示
第2关:逻辑表示法
#encoding=utf8
'''
请将下面代码空缺部分补全
'''
def x(p):
#********* Begin *********#
if p == '打雷':
q = '下雨'
elif p == '动物会飞会下蛋':
q = '该动物是鸟'
#********* End *********#
print(q)第3关:框架表示法
#encoding=utf8
def d():
#********* Begin *********#
d = {'name':'蔡徐坤','age':21,'hobby':'rap','sex':'male'}
#********* End *********#
return d产生式表示法与框架表示法
第1关:产生式表示法
1、下面哪个选项是确定性规则知识的产生式表示的基本形式( )
A、IF P THEN Q
2、老李的年龄可能是40岁,表示为(Li,Age,40,0.8),这属于哪种表示法( )
D、不确定性事实知识的产生式表示
3、产生式与谓词逻辑的蕴含式的基本形式相同,但蕴含式只是产生式的一种特殊情况。
A、对
4、下列关于产生式表示法的特点,那些是产生式表示法的优点( )
A、自然性
B、模块性
C、清晰性
D、有效性
5、以下适合用产生式表示法表示的是( )
A、化学反应方面的知识
B、医疗诊断方面的知识
C、故障诊断方面的知识
D、领域问题的求解
第2关:产生式系统
# 动物识别系统
# 自定义函数,判断有无重复元素
def judge_repeat(value, list=[]):
for i in range(0, len(list)):
if (list[i] == value):
return 1
else:
if (i != len(list) - 1):
continue
else:
return 0
# 自定义函数,对已经整理好的综合数据库real_list进行最终的结果判断
def judge_last(list):
for i in list:
if (i == '23'):
for i in list:
if (i == '12'):
for i in list:
if (i == '21'):
for i in list:
if (i == '13'):
print("黄褐色,有斑点,哺乳类,食肉类->金钱豹\n")
print("所识别的动物为金钱豹")
return 0
elif (i == '14'):
print("黄褐色,有黑色条纹,哺乳类,食肉类->虎\n")
print("所识别的动物为虎")
return 0
elif (i == '14'):
for i in list:
if (i == '24'):
print("有黑色条纹,蹄类->斑马\n")
print("所识别的动物为斑马")
return 0
elif (i == '24'):
for i in list:
if (i == '13'):
for i in list:
if (i == '15'):
for i in list:
if (i == '16'):
print("有斑点,有黑色条纹,长脖,蹄类->长颈鹿\n")
print("所识别的动物为长颈鹿")
return 0
elif (i == '20'):
for i in list:
if (i == '22'):
print("善飞,鸟类->信天翁\n")
print("所识别的动物为信天翁")
return 0
#********* Begin *********#
elif (i == '22'):
for i in list:
if (i == '15'):
for i in list:
if (i == '16'):
for i in list:
if (i == '4'):
print("不会飞,长脖,长腿,鸟类->鸵鸟\n")
print("所识别的动物为鸵鸟")
return 0
# ********* End *********#
elif (i == '4'):
for i in list:
if (i == '22'):
for i in list:
if (i == '18'):
for i in list:
if (i == '19'):
print("不会飞,会游泳,黑白二色,鸟类->企鹅\n")
print("所识别的动物企鹅")
return 0
else:
if (list.index(i) != len(list) - 1):
continue
else:
print("\n根据所给条件无法判断为何种动物")
第3关:框架表示法
1、产生式表示法是一种结构化的知识表示方法,现在已经在多种系统中得到应用。
B、错
2、如下图是一个教室框架,该框架共有( )槽
B、13
3、下列选项中,哪些是框架表示法的特点( )
A、结构性
C、继承性
D、自然性
搜索问题与技术
第1关:搜索策略
1、若将搜索问题看成是走迷宫,搜索空间越大,则迷宫越大
A、正确
2、常用的搜索策略方式为盲目搜索与启发式搜索
A、正确
3、下列说法正确的是
B、广度优先搜索算法属于盲目搜索
C、搜索问题的解可能有多个
D、A*算法属于启发式搜索
第2关:盲目搜索
def PlayMazz(mazz, start, end):
'''
走迷宫,从start走到end
:param mazz: 迷宫
:param start: 迷宫的起点
:param end: 迷宫的出口
'''
# queue为队列,当队列为空或者当前地点为H时搜索结束
visited, queue = set(), [start]
while queue:
# 从队列中出队,即当前所处的地点
vertex = queue.pop(0)
if vertex not in visited:
visited.add(vertex)
print(vertex, end='')
#********* Begin *********#
#当走到出口时结束算法
if vertex == end:
return
#********* Begin *********#
# 将当前所处地点所能走到的地点放入队列
for v in mazz[vertex]:
if v not in visited:
queue.extend(v)第3关:启发式搜索 - 扫地机器人最短路径搜索
from a_star_utils import Node
def A_star(map, mapSize, start, end):
'''
A*算法,从start走到end
:param map:地图
:param mapSize:地图大小,例如[10,10]表示地图长10宽10
:param start:表示出发地,类型为列表,如[1,2]表示出发地为地图中的第1行第2列的方块
:param end:表示目的地,类型为列表,如[1,2]表示目的地为地图中的第1行第2列的方块
:return:从出发地到目的地的路径
'''
openedList = []
#********* Begin *********#
# 获得出发地方块的信息,并将信息保存为node变量
node = map[start[0]][start[1]]
#********* End *********#
node.distanceFromOri = 0
node.allDistance = 0
#********* Begin *********#
# 将当前方块存到开启列表中
openedList.append (node)
node.added = True
#********* End *********#
while len(openedList) != 0:
node = openedList.pop(0)
node.closed = True
if node.y == end[0] and node.x == end[1]:
finalListNeedReverse = []
while node != None:
finalListNeedReverse.append(node)
node = node.parent
finalListNeedReverse.reverse()
return finalListNeedReverse
neighboursList = []
y = node.y
x = node.x
parentDistanceFromOri = node.distanceFromOri
for needNodey in (y + 1, y, y - 1):
if needNodey < 0 or needNodey >= mapSize[0]:
continue
for needNodex in (x + 1, x, x - 1):
if needNodex < 0 or needNodex >= mapSize[1]:
continue
needNode = map[needNodey][needNodex]
if needNode.unable == True or needNode.closed == True or needNode.added == True:
continue
yOffset = needNodey - y
xOffset = needNodex - x
allOffset = yOffset + xOffset
if allOffset == 1 or allOffset == -1:
distanceFromOri = parentDistanceFromOri + 1
else:
distanceFromOri = parentDistanceFromOri + 1.4
if needNode in neighboursList:
# 若新的G值比老的G值低,则更新成老的G值
if distanceFromOri < needNode.distanceFromOri:
needNode.distanceFromOri = distanceFromOri
else:
needNode.distanceFromOri = distanceFromOri
neighboursList.append(needNode)
for needNode in neighboursList:
needNode.parent = node
# 更新F值
needNode.allDistance = needNode.distanceFromOri + needNode.distanceFromDes
needNode.added = True
openedList.append(needNode)
openedList.sort(key=lambda x: x.allDistance)
return None第4关:搜索算法应用 - 四皇后问题
def make(mark):
'''
标记皇后的位置,例如mark[0] = 2, 表示第1行皇后放在第3列的位置
:param mark: 皇后的位置信息
:return: 拼接好的结果
'''
#初始化数组
r = [['X' for _ in range(len(mark))] for _ in range(len(mark))]
#将每一行中皇后的位置用‘Q’代替
for i in mark:
r[i][mark[i]] = 'Q'
#枚举,将原来散的元素连接成字符串
for k, v in enumerate(r):
r[k] = ''.join(v)
return r
def FourQueens(mark, cur, ret):
'''
深度优先搜索的方式求解四皇后问题
:param mark:表示皇后的位置信息,例如[0,1,3,2]表示棋盘的第1行第1列,第2行第2列,第3行第4列,第4行第3列放置了皇后。例如[1, None, None, None]表示第1行第2列放置了皇后,其他行没有放置皇后。初始值为[None,None,None,None]
:param cur:表示当前准备在第几行放置皇后,例如`cur=1`时,表示准备在第`2`行放置皇后。初始值为0
:param ret:表示存放皇后摆放结果的列表,类型为列表。初始值为[]
:return:无
'''
if cur == len(mark):
#********* Begin *********#
# 如果当前行是最后一行,记录一个解,并返回结束此次搜索
ret.append(make(mark))
return
#********* End *********#
#试探处理,将当前行的皇后应该在的位置遍历每一列,如果满足条件,递归调用处理下一行
for i in range(len(mark)):
mark[cur], down = i, True
for j in range(cur):
# 当想在当前位置放皇后会与其他皇后冲突时不放置皇后
if mark[j] == i or abs(i-mark[j]) == cur - j:
down = False
break
if down:
# 准备在下一行找能放置换后的位置
FourQueens(mark, cur+1, ret)第十三章 不确定性的量化
第1关:第十三章 不确定性的量化习题
1、下列式子成立的是( )
C、P(AB)=P(A)·P(B|A)
2、下列关于不确定性说法正确的是:
B、概率提供了一种方法以概括由我们的惰性和无知产生的不确定性,由此解决限制问题
3、设两个独立事件A和B都不发生的概率为1/9,A发生B不发生的概率与B发生A不发生的概率相同则事件A发生的概率P(A)是:
A、2/3
第十四章 概率推理
第1关:第十四章 概率推理习题
1、已知事件A与事件B发生与否伴随出现,根据贝叶斯公式可得到P(B|A)=P(A|B)*M/P(A),则M=()
D、P(B)
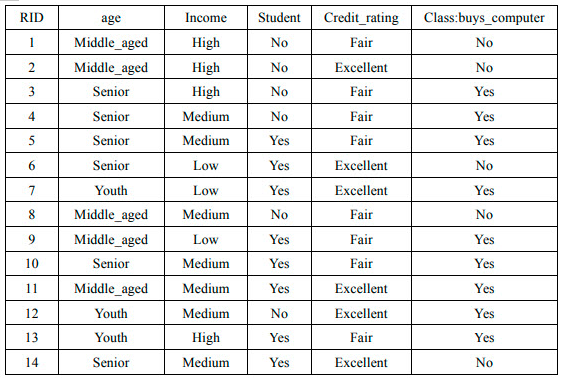
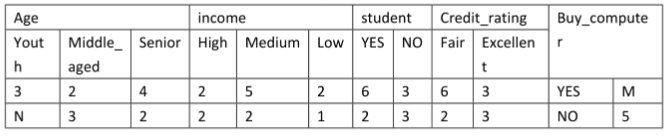
2、通过对某地区的部分人群进行调查,获得了他们对于的age、income、是否为student、Credit_rating以及是否购买某品牌的电脑的信息进行了记录。训练样例如表1,通过训练样例得到表2,表3为根据表2的统计数据,得到的在分类为YES和NO的条件下各个属性值取得的概率以及YES和NO在所有样例中取值的概率。
表1
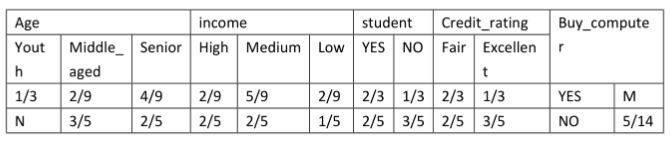
表2
表3
x(age=youth,income=medium,student=no,credit_rating=excellent),则P(NO|x)=()
B、0.23
3、贝叶斯网络主要应用的领域有()
A、模式识别
B、辅助智能决策
C、医疗诊断
D、数据融合
4、关于贝叶斯网络的描述正确的是()
A、它时一种帮助人们将概率统计应用于复杂领域、进行不确定性推理和数据分析的工具。
D、它是有向无环图
5、给定贝叶斯公式P( cj|x) =(P(x|cj)P(cj))/P(x),公式中P( cj|x)为()
B、后验概率
第九章 一阶逻辑的推理
第1关:第九章 一阶逻辑的推理习题
1、习题 2 :构造下面推理的证明:每个喜欢步行的人都不喜欢坐汽车。每个人或者喜欢坐汽车或者喜欢骑自行车。有的人不喜欢骑自行车,因而有的人不喜欢步行(个体域为人类集合)
下列说法正确的是:
B、前提:∀x ( F ( x ) ⇒¬G ( x ) ) , ∀x ( G(x) V H(x) ) , ∀ x ( H(x) )
2、习题 2 :构造下面推理的证明:每个喜欢步行的人都不喜欢坐汽车。每个人或者喜欢坐汽车或者喜欢骑自行车。有的人不喜欢骑自行车,因而有的人不喜欢步行(个体域为全总个体域)
下列选项错误的是:
C、结论:∃ x ( ¬M(x)∧¬ F(x))
第八章 一阶逻辑
第1关:第八章 一阶逻辑习题
1、下列答案中哪个是错的?
用谓词表达式写出下列命题:
(1)王文不是学生;
(2)2是素数且是偶数;
(3)若m是奇数,则2m不是奇数;
(4)河北省南接河南省;
(5)若2大于3.则2大于4.
E、S(x,y):x大于y a:2 b:3 c :4
于是(5)为:S(a,b) ⇒S(b,c)
2、用谓词表达式写出下列命题:
(1)凡是有理数都可以写成分数;
(2)存在着会说话的机器人;
(3)并非每个实数都是有理数;
(4)如果有限个数的乘积为零,那么至少有一个因子等于零;
(5)没有不犯错误的人。
下列答案中哪项错误?
C、R(x):x是实数 Q(x):x是有理数
于是 (3)为: (∀x)(R(x) ⇒Q(x))
E、M(x):x为人 F(x):x犯错误
于是 (5)为: ∃x(F(x)∧M(x))