目录
一、函数递归的定义和条件
1.递归的定义
程序调用自身的编程技巧称为递归( recursion)。表示一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
递归的主要思考方式在于:把大事化小
2.递归的两个必要条件
(1)存在限制条件,当满足这个限制条件的时候,递归便不再继续。
(2)每次递归调用之后越来越接近这个限制条件。
二、基本思想
1.我们在写递归代码时,首先就需要一个能够完成任务的具体思路。
2.运用递归大事化小的思维,写出每一步的步骤。
3.写出相应完成任务的函数,但我们不需要考虑它内部的执行的整个过程。
4.根据结果仔细考虑终止递归的条件。
5.在写代码的时候只需要考虑前两步即可。
三、实例讲解
1.汉诺塔问题
(1)问题描述
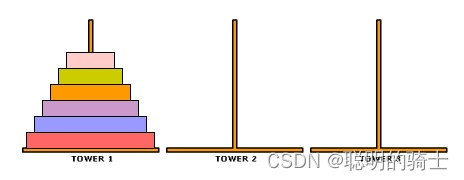
汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
任务:把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
规定:在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
相当于在保证每根柱子上小圆盘下是大圆盘的条件下,把1柱上的圆盘通过柱2全部移动到柱3上。
(2)思路分析
- 基本思路
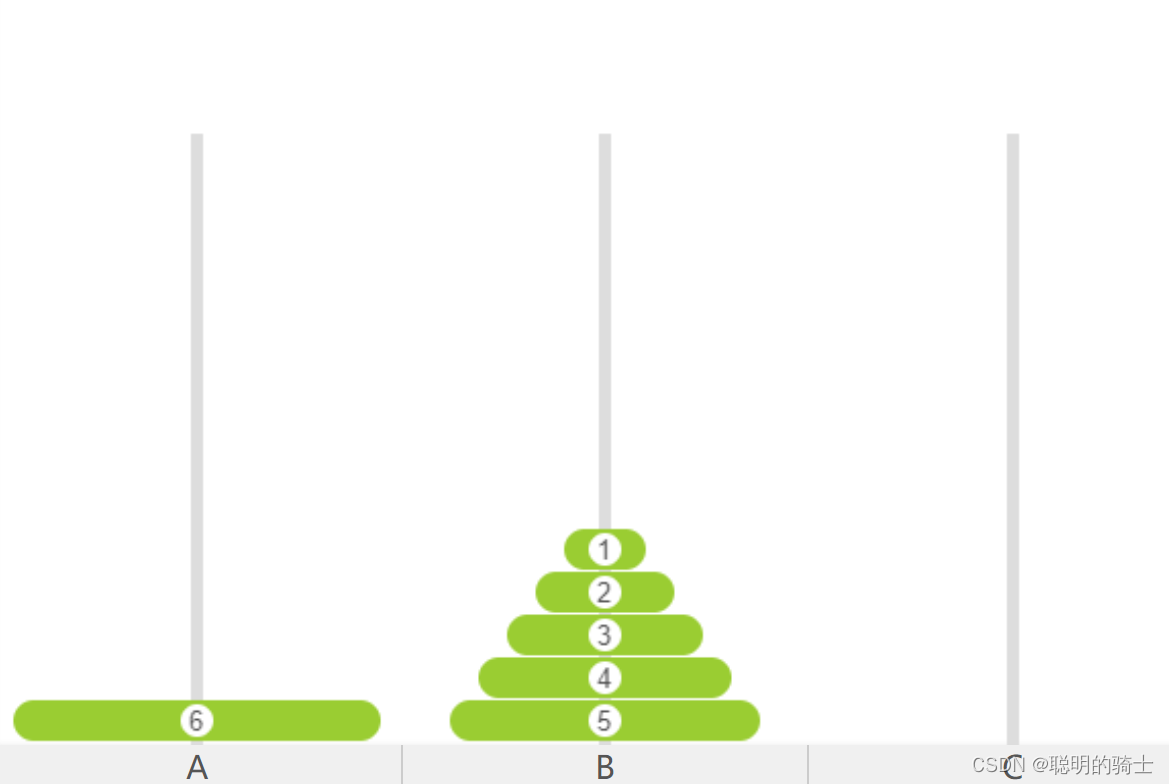
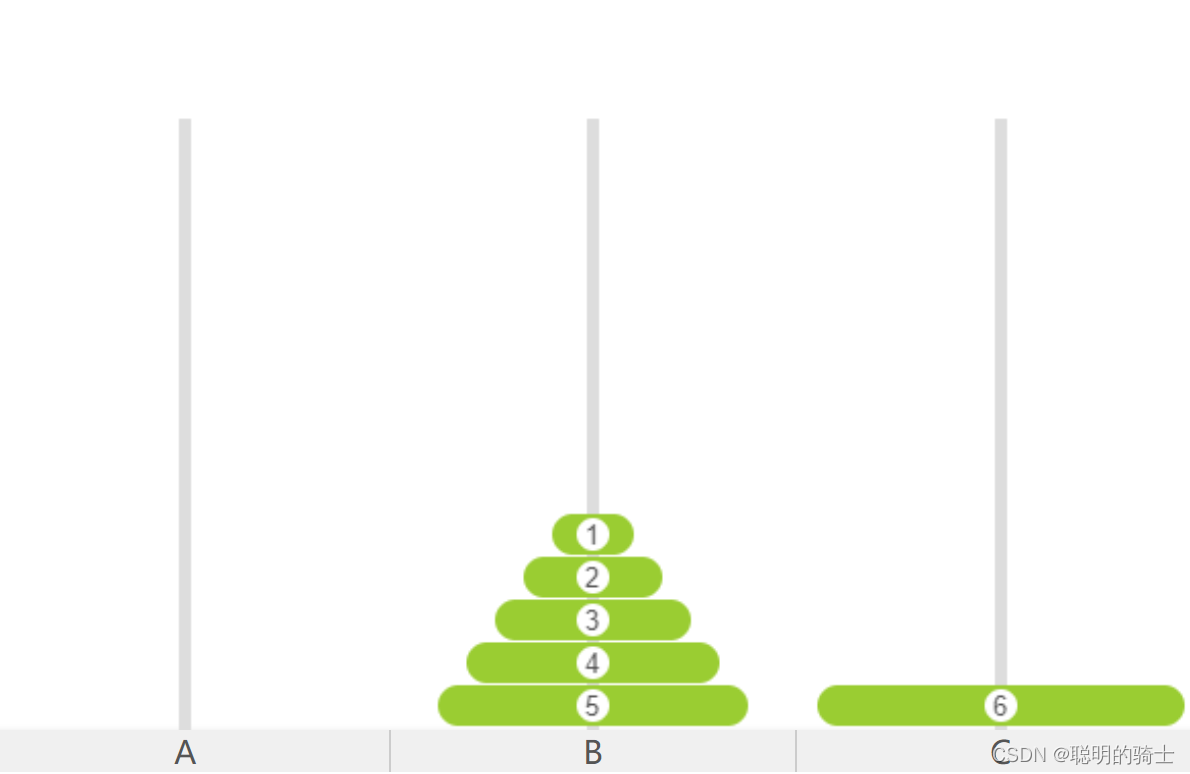
柱1上一共有六个圆盘,我们可以先把上面的五个圆盘整体挪动到第二根柱子上,然后把柱1的最下面的圆盘挪到柱3上,最后再把柱2上的五个圆盘整体挪动柱3上。
- 函数定义
我们此时定义一个函数叫hanoi,它可以完成把规定数量的圆盘从一个柱子移动到另一个柱子上。
- 递归结束的判断
我们需要把柱1的六个圆盘移动到柱3上。
如果我们需要移动最下面的第六个圆盘,就需要先移走上面的五个圆盘。
如果我们需要移动第五个圆盘,就又需要先移走上面的四个圆盘。
如果我们需要移动第四个圆盘,就双需要先移走上面的三个圆盘。
如果我们需要移动第三个圆盘,就叒需要先移走上面的二个圆盘。
如果我们需要移动第二个圆盘,就叕需要先移走上面的一个圆盘。
最后在我们只剩下一个圆盘时,我们就可以直接移动了。
此时,我们的递归此时就可以中断了,所以我们得到递归终止的判断依据:柱1上的圆盘数小于等于一时,跳出递归。
(3)代码书写
#include<stdio.h>
void move(char a,char c)
{
printf("%c->%c ", a, c);
}
void hanoi(int n, char a, char b, char c)
{
if (n > 1)
{
hanoi(n - 1, a, c, b);//
move(a, c);//
hanoi(n - 1, b, a, c);//
}
else
{
move(a, c);
}
}
int main()
{
int n = 0;
printf("请输入需要移动的圆盘个数:");
scanf("%d", &n);
hanoi(n,'A','B','C');//移动A上的所有圆盘到C上
return 0;
}2.青蛙跳台阶问题
(1)问题描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
任务:青蛙跳上一个 n 级的台阶总共有多少种跳法。
规定:青蛙一次可以跳一个或两个台阶。
(2)思路分析
- 基本思路
我们可以先计算一下再台阶较少时的跳跃方式的种数。
一级台阶:青蛙直接跳上去,共一种方式。
二级台阶:青蛙跳一级再跳一级;青蛙直接跳上两级,共两种。
三级台阶:青蛙跳一级三次;青蛙跳一级再跳两级;青蛙跳两级再跳一级,共三种。
四级台阶:青蛙跳一级四次;青蛙跳两级再跳一级再跳一级;青蛙跳一级再跳两级再跳一级;青蛙跳一级再跳一级再跳两级青蛙;青蛙跳两级再跳两级,共五种。(后面就不一一列举了)
五级台阶:共八种
六级台阶:共十三种
......
从这里我们可以看到,随着台阶级数的升高,青蛙跳台阶的可能情况满足斐波那契数列的条件。(这里的元素满足从第三项开始,前面两项的和等于这一项,但元素的前两位不是1)
- 函数定义
我们此时定义一个函数叫frog,它可以完成计算这个数列的第n个元素。
- 递归结束的判断
比如说,青蛙需要跳上五级台阶。
为了找到五级台阶的种数,我们需要找到四级台阶和三级台阶的数值。
为了找到四级台阶的种数,我们需要找到三级台阶和二级台阶的数值,此时其中一个数值不需要递归了。
为了找到三级台阶的种数,我们需要找到二级台阶和一级台阶的数值,此时另一个数值也不需要递归了。
此时,我们的递归此时就可以中断了,所以我们得到递归终止的判断依据:柱1上的圆盘数小于等于一时,跳出递归。
(3)代码书写
#include<stdio.h>
int frog(int m)
{
int sum = 0;
if (m == 1)//等于1时,sum=1
{
sum += 1;
}
else if (m == 2)//等于2时,sum=2
{
sum += 2;
}
else//大于3时,开始递归
{
sum = frog(m - 1) + frog(m - 2);
}
return sum;
}
int main()
{
int n = 0;
printf("请输入台阶的个数:");
scanf("%d", &n);
int m = frog(n);
printf("青蛙跳上台阶的选择共有%d种\n", m);
return 0;
}三、总结
对于我自己而言,写递归一般是这样的步骤:
1.仔细看好题目的要求,思考你可以进行的操作。
2.根据你自己可以使用的操作,运用大事化小的思想或者通项公式的思想写出每一步。
(1)大事化小
按顺序打印数字的每一位:print函数实现
print(1234)
print(123) printf("4 ")
print(12) printf("3 ") printf("4 ")
print(1) printf("2 ") printf("3 ") printf("4 ")
printf("1 ") printf("2 ") printf("3 ") printf("4 ")
(2)通项公式
斐波那契数列表示为An
A1=1,A2=1,A3=A1+A2,A4=A2+A3,A5=A3+A4 。。。。。。
3.根据递归的运行确定递归终点的判据(这一步很重要)
4.只看前两步,写出代码即可。
//按顺序打印数字的每一位:print函数实现
void print(int n)
{
if(n>9)//判断依据
{
print(n/10);//这个代码实现了个位前数字的打印,不需要管它内部的运行流程
}
printf("%d ", n%10);//这个代码打印个位
}int fib(int m)
{
int ret = 0;
if (m<=2)
{
ret = 1;//第一二项为1
}
else
{
ret = fib(m - 1) + fib(m - 2);//三项及三项以后,后一项等于前两项的和
}
return ret;
}