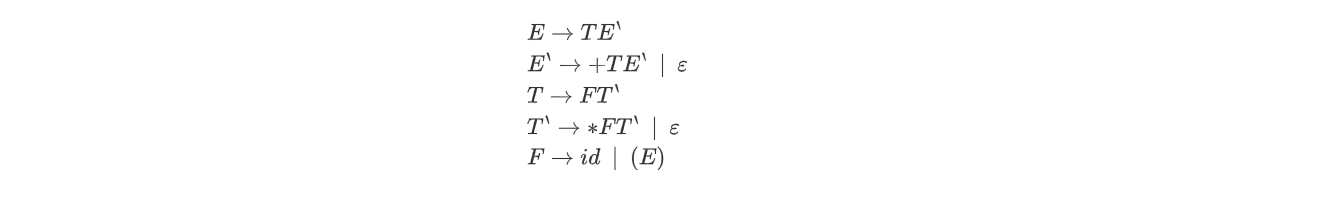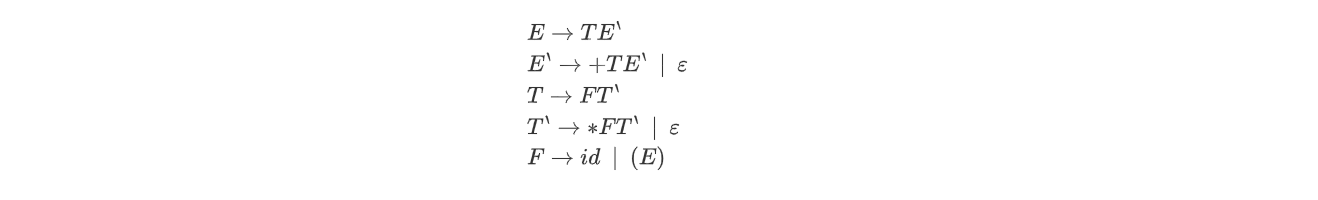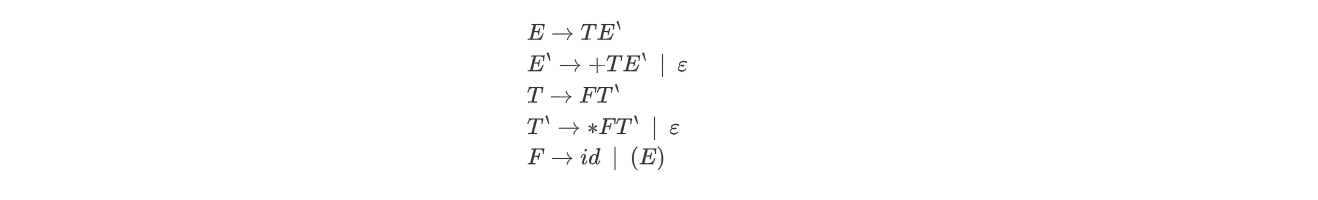LL(1)文法判断

前言：

​  在自然语言中，文法是文章的书写法规，一般用来指以文字、词语、短句、句子的编排而组成的完整语句和文章的合理性组织。

  而文法在计算机中是设计师制定的一些规则，编译器通过这些规则可以识别出程序设计语言的语义，然后通过分析编译出语言（代码）要表达的效果，它就像是编译器的大脑，没有它编译器就不能识别这些编程语言。而今天要讲的LL(1)文法是计算机文法中的一种，需要注意的是，并不是所有的语言都可以用LL(1)文法来描述，而且不存在判定某语言是否是LL(1)文法的算法。也就是说，确定的自顶向下分析只能实现一部分上下文无关语言的分析，这就是LL(1)文法所产生的语言。

​ LL(1)文法定义如下：
$$\begin{array}{rl}& 对文法G的句子进行确定的自顶向下语法分析的充分必要条件是，G的任意两个具有相同左部的产生式A\to \alpha |\beta 满足下列条件:\\ & (1)如果\alpha 、\beta 均不能推导出\epsilon ，则FIRST(\alpha )\cap FIRST(\beta )=\varphi \\ & (2)\alpha 和\beta 至多有一个能推导出\epsilon \\ & (3)如果\alpha \to \epsilon ，则FIRST(\alpha )\cap FOLLOW(A)=\varphi \end{array}$$
将满足上述条件的文法称为LL(1)文法。

注：希腊字母代表不同的非终结符跟终结符组成的序列，小写字母代表终结符，大写字母代表非终结符，id代表数字，#是输入结束符，ε是空, ...表示若干个终结符或者非终结符或者空

🐳LL(1)文法判断方法

LL(1)文法共有两种判断法：

• 通过定义判断，满足前言中的定义则是LL(1)文法，具体步骤如下：

  • 消除左递归

  • 计算出FIRST集合

  • 计算出FOLLOW集合

  • 存在产生式 A→α|β，如果α、β均不能推导出ε，则需满足： FIRST(α) ∩ FIRST(β) =∅

  • 存在产生式 A→α|β，如果α 和 β 至多有一个能推导出 ε

    1）假设是 α 能推导出 ε，则要满足：FIRST(α) ∩ FOLLOW(A) = ε

    2）假设α 和 β 都不能推导出 ε，则直接满足条件

• 通过SLECT集合求解

  • 消除左递归
  • 计算出FIRST集合
  • 计算出FOLLOW集合
  • 通过FIRST集合和FOLLOW集合计算出SELECT集合
  • 左部符号相同的SELECT集合进行交集运算，交集结果为空，则符合LL(1)文法

🐳左递归的消除

引言：

  左递归，是计算机科学里面一种递归的特殊状况。在上下文无关文法内的说法，若一个非终端符号（non-terminal）r有任何直接的文法规则或者透过多个文法规则，推导出的句型（sentential form）其中最左边的符号又会出现r，则我们说这个非终端符号r是左递归的。

• 左递归的定义：一个文法是左递归的，若我们可以找出其中存在某非终端符号A，最终会推导出来的句型(sentential form)里面包含以自己为最左符号(left-symbol)的句型。

• 左递归的分类：

  • 直接左递归：
    $$A\to A\alpha |\beta$$

  • 间接左递归：
    $$\begin{array}{rl}& A\to B\alpha \\ & B\to ...\to A\beta \end{array}$$

• 递归消除方法：

  • 对于直接左递归：
    $$\begin{array}{rl}& A\to \beta A^{‘}\\ & A^{‘}\to \alpha A^{‘}|\epsilon \end{array}$$

  • 对于间接左递归：

    1）把给定的文法G中所有非终结符按任意顺序排列，并编号

    2）若产生式右部最左的符号是非终结符，且这个非终结符序号大于左部非终结符，则暂不处理

    3）若序号小于左部的非终结符，则用序号小的产生式的右部来替换左部

    4）若消除过程中出现了直接左递归，就按照直接左递归的方法，来消除

    5）删除其中不可达的非终结符¹

Step1:把文法G的所有非终结符按任意顺序排列，并编号
A_1、B_2、C_3


Step2:按照顺序遍历G中的非终结符，根据规则2）、3）、4）进行判断
对于A:
A的下标是1，右部是B,而B的下标是2大于1，故暂不处理

对于B:
同理，B也暂不处理

对于C:
C的下标大于右部A的下标，故进行替换
替换后的结果为:C → Bαγ | αγ | γ

此时C的下标仍然大于右部非终结符，故进行替换
替换后的结果为:C → Cαβγ | αβγ | αγ | γ

此时出现直接递归，则按照直接递归的方法来消除递归
消除后的结果为:
C → αβγC` | αγC` | γC`
C` → αβγC` | ε

Step3:删除其中不可达的非终结符，这里是A、B
所以文法G经过消除左递归后的最终结果为：
C → αβγC` | αγC` | γC`
C` → αβγC` | ε

备注：第一步对非终结符按任意方式排序，最后结果的产生式有可能不同，但它们是等价的

🐳FIRST集合求解

First 集合的定义：

这是百度上的介绍，有点晦涩难懂，总结来讲就是：一个文法符号串所可能推导出的符号串的第一个终结符的集合

FIRST集合求解规则：

• 单个终结符的FIRST集合是它本身

• 单个非终结符的FIRST集合

  • A → a…   此时 a∈FIRST(A)
  • A → B…   ε ∉ FIRST(B)，此时 FIRST(B)⊆FIRST(A)
    A → Bα…  ε ∈ FIRST(B)，此时FIRST(A) = FIRST(B)UFIRST(α)
    后续是递推关系……
  • A → B…|α…   此时 FIRST(A) = FIRST(B)UFIRST(α)

• 多个符号的的FIRST集合

  • FIRST(aAB…) = {a}

  • FIRST(AB…) = FIRST(A)（假设 ε ∉ FIRST(A)）；

    当 ε∈FIRST(A)， ε ∉FIRST(B) 时，FIRST(AB…) = FIRST(A)UFIRST(B…)；

    后续是递推关系……

First集合中的符号一定是终结符，终结符也包括空串ε

🌰举个例子，求下列文法G的FIRST集合：

• Step1：通过第一个产生式可以知道： FIRST(T)⊆FIRST(E)，此时不知道FIRST(T)暂且放在这不管

• Step2：通过第二个产生式可以知道：{+,ε}⊆FIRST(E`)

• Step3：通过第三个产生式可以知道：FIRST(F)⊆FIRST(T)，此时不知道FIRST(F)暂且放在这不管

• Step4：通过第四个产生式可以知道：{*,ε}⊆FIRST(T`)

• Step5：通过第五个产生式可以知道：{id,(}⊆FIRST(F)

  此时已知FIRST(F)，往回代入Step3，从而求得FIRST(T)={id,(}；

  又将求得的FIRST(T)回代入Step1，从而求得FIRST(E)={id,(}

综上可知，上面各非终结符的FIRST集合为：

🐳FOLLOW集合求解

引言：

​ 这是书上的定义：

书上说通过（2）和（3）的重复使用可以求出A的FOLLOW集合，刚开始看有点不太懂，后来通过做题实践，总结了求FOLLOW集合的一般性步骤，现在就让我们来看一下怎么如何简便求解FOLLOW集合吧😃

重点：
假如我们要求的是U的FOLLOW集合，其中U存在几种形式：
1.    U → . . .                    此 时 # ∈ U                                                                                                                                                       2.    A → . . . U a             此 时 a ∈ F O L L O W ( U ) , 与 A 无 关 3.    A → . . . U P . . .        此 时 { F I R S T ( P ) − { ε } } ⊆ F O L L O W ( U ) , 与 A 无 关 4.    A → . . . U P            若 ε ∈ F I R S T ( P ) ， 此 时 F O L L O W ( A ) ∪ { F I R S T ( P ) − { ε } } ⊆ F O L L O W ( U ) 5.    A → . . . U                此 时 F O L L O W ( A ) ⊆ F O L L O W ( U ) \begin{aligned} &1.~~U\rightarrow{...}~~~~~~~~~~~~~~~~~~此时\#\in{U}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ &2.~~A\rightarrow{...Ua}~~~~~~~~~~~此时a\in{FOLLOW(U)},与A无关\\ &3.~~A\rightarrow{...UP...}~~~~~~此时\{FIRST(P)-\{\varepsilon\}\}\subseteq{FOLLOW(U)},与A无关\\ &4.~~A\rightarrow{...UP}~~~~~~~~~~若\varepsilon\in{FIRST(P)}，此时FOLLOW(A)\cup{\{FIRST(P)-\{\varepsilon\}\}}\subseteq{FOLLOW(U)}\\ &5.~~A\rightarrow...U~~~~~~~~~~~~~~此时FOLLOW(A)\subseteq{FOLLOW(U)} \end{aligned} ​1.  U→...                  此时#∈U                                                                                                                                                     2.  A→...Ua           此时a∈FOLLOW(U),与A无关3.  A→...UP...      此时{FIRST(P)−{ε}}⊆FOLLOW(U),与A无关4.  A→...UP          若ε∈FIRST(P)，此时FOLLOW(A)∪{FIRST(P)−{ε}}⊆FOLLOW(U)5.  A→...U              此时FOLLOW(A)⊆FOLLOW(U)​
拓展：
*当 A → . . . U P D . . . 时 ， 且 ε ∈ P 且 ε ∉ D 时 , F O L L O W ( U ) = { F I R S T ( P ) − ε } ∪ F O L L O W ( P ) ， 其 中 F O L L O W ( P ) 可 以 根 据 规 则 3. 来 求 解 A\rightarrow{...UPD...}时，且ε\in{P}且ε∉ {D}时,FOLLOW(U)=\{{FIRST(P)−{ε}}\}\cup{FOLLOW(P)}，其中FOLLOW(P)可以根据规则3.来求解 A→...UPD...时，且ε∈P且ε∈/​D时,FOLLOW(U)={FIRST(P)−ε}∪FOLLOW(P)，其中FOLLOW(P)可以根据规则3.来求解
这是存在一种递推关系的，后面可以无限递推下去

在此，详细说明以下形式3.、形式4.和形式5.的关系
形式4.是形式3.的特例，当形式3.中…为ε，且ε∈FIRST(P）时，形式4.等于形式3.
形式5.是形式4.的特例，当形式4.中的P=ε时，就是形式5.

FOLLOW(U)通过上面1、2、3、4、5条规则进行求解，同时应当注意：Follow集合中的符号一定是终结符，但是不能包括空串ε

通过做题我们可以知道FOLLOW集合就是文法符号后面可能跟随的终结符的集合（不包括空 串ε）

🌰举个例子，求下列文法G的FOLLOW集合：

上面我们求得了文法G的FIRST集合，如下：

现在让我们继续来求FOLLOW集合：

• Step1：由形式1.可以知，所有的非终结符的FOLLOW集合都具有{#}

• Step2：求FOLLOW(E)，第五个产生式满足形式2.，所以)∈FOLLOW(E)，此时FOLLOW(E)={#,)}

• Step3：求FOLLOW(E`)，第一个产生式满足形式5.，所以FOLLOW(E)⊆FOLLOW(E’)，此时FOLLOW(E’)={#,)}

• Step4：求FOLLOW(T)，第一个产生式满足形式4.,所以
  FOLLOW(E)⊆FOLLOW(T)；第二个产生式满足形式3.，所以

  {FIRST(E`)-{ε}}⊆FOLLOW(T)，此时FOLLOW(T)={#,),+}

• Step5：同理可求得FOLLOW(T`)={#,),+}

• Step6：同理，FOLLOW(F)={#,),+,*}

综上可知，上面各非终结符的FOLLOW集合为：

🐳SELECT集合求解

SELECT集合就是产生式左部的可能的推导结果的起始符号
A → α   同 时   ε ∉ F I R S T ( α ) 此 时 S E L E C T ( A → α ) = { F I R S T ( α ) − { ε } } A → α   同 时   ε ∈ F I R S T ( α ) 此 时 S E L E C T ( A → α ) = { F I R S T ( α ) − { ε } } ∪ F O L L O W ( A ) \begin{aligned} &A\rightarrow{\alpha}~同时~\varepsilon∉FIRST(\alpha)\qquad此时SELECT(A\rightarrow{\alpha}) = \{FIRST(\alpha)-\{\varepsilon\}\}\\ &A\rightarrow{\alpha}~同时~\varepsilon\in FIRST(\alpha)\qquad此时SELECT(A\rightarrow\alpha)=\{FIRST(\alpha)-\{\varepsilon\}\}\cup FOLLOW(A) \end{aligned} ​A→α 同时 ε∈/​FIRST(α)此时SELECT(A→α)={FIRST(α)−{ε}}A→α 同时 ε∈FIRST(α)此时SELECT(A→α)={FIRST(α)−{ε}}∪FOLLOW(A)​
注：SELECT集合中不包括空串ε，但有可能会包含#

🌰举个例子，求下列文法G的SELECT集合：

上面我们求得了文法G的FIRST集合和FOLLow集合，如下：

现在继续来求SELECT集合：
∉

• Step1：对于第一个产生式，ε∉FIRST(TE‘)，所以SELECT(E → TE’) = { FIRST(TE’ ) - {ε} }={ ( , id }

• Step2：对于第二个产生式，有两种情况：

  当E’ → +TE’，ε∉FIRST(+TE`)，所以SELECT(E’ → +TE’) = {FIRST(+TE’) - {ε}}= {+}

  当E’ → ε，显然 ε∈FIRST(ε)，所以SELECT(E’ → ε) = FOLLOW(E’) = {#,)}

• Step3：同理可求得SELECT(T → FT’) = {(,id}

• Step4：SELECT(T’ → *FT’) = {*}
      ​ SELECT(T’ → ε) = {#,),+}

• Step5：SELECT(F → id) = {id}
  ​     SELECT(F → (E)) = {(}

LL(1)文法预测分析表的构造可以参观这篇文章的大题编译原理期末复习重点

🐳实战例题

$例1:$
$$\begin{array}{rl}& 判断下列文法G是否是LL(1)文法\\ & E\to E+T|T\\ & T\to T\ast F|F\\ & F\to id|(E)\end{array}$$

• Step1：消除左递归
  $$\begin{array}{rl}& E\to T{E}^{‘}\\ & E^{‘}\to +T{E}^{‘}|\epsilon \\ & T\to F{T}^{‘}\\ & T^{‘}\to \ast F{T}^{‘}|\epsilon \\ & F\to id|(E)\end{array}$$

• Step2：求FIRST集合

  非终结符	FIRST	FOLLOW
  E	（，id
  E’	+，ε
  T	（，id
  T‘	*， ε
  F	（，id

  需要注意的是（ ，） ， ε 和 id 都是终结符

• Step3：求FOLLOW集合

  非终结符	FIRST	FOLLOW
  E	（，id	#，）
  E‘	+，ε	#，）
  T	（，id	#，），+
  T’	*， ε	#，），+
  F	（，id	#，），+，*

• Step4：求SELECT集合

  产生式	SELECT集合
  E → TE’	( , id
  E’ → +TE’	+
  E’ → ε	#，）
  T → FT’	（，id
  T’ → *FT’	*
  T’ → ε	#，），+
  F → id	id
  F → (E)	（

• Step5：对左部相同的产生式的SELECT集合进行交集运算

  SELECT(E’ → +TE’) ∩ SELECT(E’ → ε) = ε

  SELECT(T’ → *FT’) ∩ SELECT(T’ → ε) = ε

  SELECT(F → id) ∩ SELECT(F → (E)) = ε

  从上面可以知道，所有左部相同的SELECT集合的交集运算结果都是ε，所以文法G是LL(1)文法

$$\begin{array}{rl}例2:& \\ & 求以下文法G[S]是否是LL(1)文法，并且给出判断过程，的的FIRST集合和FOLLOW集合:\\ & S\to MH|a\\ & H\to LSo|\epsilon \\ & K\to dML|\epsilon \\ & L\to eHf\\ & M\to K|bLM\end{array}$$
$解：$

• Step1：消除左递归。显然文法G[s]不存在左递归，故无需消除左递归

• Step2：求FIRST集合。

  ①对于产生式1，$S\to MH=>FIRST(M)\subseteq FIRST(S)，FIRST(M)$暂且不知道，所以先不管，$S\to a=>a\in FIRST(S)$；
  ②对于产生式2，$H\to LSo=>FIRST(L)\subseteq FIRST(H)，FIRST(L)暂且不知道，所以先不管$，$H\to \epsilon =>\epsilon \in FIRST(H)$；
  ③对于产生式3，$K\to dML=>d\in FIRST(K),$$K\to \epsilon =>\epsilon \in FIRST(K)$ ，所以 F I R S T ( K ) = { d , ε } ； FIRST(K)=\{d,\varepsilon\}； FIRST(K)={d,ε}；
  ④对于产生式4，$L\to eHf=>e\in FIRST(L)$，所以 F I R S T ( L ) = { e } FIRST(L)=\{e\} FIRST(L)={e}，此时已知$FIRST(L)$，将其回代到②中继而求得 F I R S T ( H ) = { e , ε } FIRST(H)=\{e,\varepsilon\} FIRST(H)={e,ε}；
  ⑤对于产生式5，$M\to bLM=>b\in FIRST(M)，$$M\to K=>FIRST(K)\subseteq FIRST(M)$，从③可知 F I R S T ( K ) = { d , ε } FIRST(K)=\{d,\varepsilon\} FIRST(K)={d,ε}，所以 F I R S T ( M ) = { b , d , ε } FIRST(M)=\{b,d,\varepsilon\} FIRST(M)={b,d,ε}，此时已知$FIRST(M)$，将其回代到①中继而求得 F I R S T ( S ) = { a , b , d , ε } FIRST(S)=\{a,b,d,\varepsilon\} FIRST(S)={a,b,d,ε}，需要注意此时ε∈FIRST(M)，所以FIRST(H)⊆FIRST(S)，故 F I R S T ( S ) = { a , b , d , e , ε } FIRST(S)=\{a,b,d,e,ε\} FIRST(S)={a,b,d,e,ε}；

  所以文法G[s]的FIRST集合如下表所示：

  非终结符	FIRST集合
  S	{a,b,d,e,ε}
  H	{e,ε}
  K	{d,ε}
  L	{e}
  M	{b,d,ε}

• Step3：求FOLLOW集合。

  ①首先我们可以发现每个非终结符都出现在产生式的右部，故每一个非终结符的FOLLOW集中都有#
  ②求$FOLLOW(S)$，从产生式2：$H\to LSo|\epsilon$ 知道o∈$FOLLOW(S)$，即 F O L L O W ( S ) = { # , o } FOLLOW(S)=\{\#,o\} FOLLOW(S)={#,o}
  ③求$FOLLOW(H)$，从产生式4可以知道 $f\in FOLLOW(H)$，从产生式1：$S\to MH|a$ 根据FOLLOW求解规则5.（不记得的可以回看）可以知道:$FOLLOW(S)\subseteq FOLLOW(H)$，所以 F O L L O W ( H ) = { # , f , o } FOLLOW(H)=\{\#,f,o\} FOLLOW(H)={#,f,o}
  ④求$FOLLOW(K)$，从从产生式5：$M\to K|bLM$，通过FOLLOW求解规则5.可以知道：$FOLLOW(M)\subseteq FOLLOW(K)$，现在FOLLOW(M)暂且不知道，先不管
  ⑤求$FOLLOW(L)$，从产生式2根据规则3.可以知道： { F I R S T ( S ) − ε } ⊆ F O L L O W ( H ) \{FIRST(S)-ε\}⊆FOLLOW(H) {FIRST(S)−ε}⊆FOLLOW(H)，同时ε∈$FOLLOW(S)$，满足求解规则2.，故$o\in FOLLOW(L)$，此时 F O L L O W ( L ) = { # , a , b , d , e , o } FOLLOW(L)=\{\#,a,b,d,e,o\} FOLLOW(L)={#,a,b,d,e,o}已经是最大的集合了，对于产生式5：$M\to K|bLM$求不求都无所谓了
  ⑥求$FOLLOW(M)$，从产生式1可以知道{FIRST(H)-ε}⊆FOLLOW(M)，同时ε∈FIRST(H)，所以满足规则4.，即：FOLLOW(S)⊆FOLLOW(M)，所以FOLLOW(M)={#,e,o}，此时已经知道了FOLLOW(M)，回代到④中从而求得FOLLOW(K)={#,e,o}

  所以非终结符的FOLLOW集合表为：

  非终结符	FIRST集合	FOLLOW集合
  S	{a,b,d,e,ε}	{#,o}
  H	{e,ε}	{#,f,o}
  K	{d,ε}	{#,e,o}
  L	{e}	{#,a,b,d,e,o}
  M	{b,d,ε}	{#,e,o}

• Step4: 求SELECT集合。

  ①求$SELECT(S\to MH)$，$\epsilon \in FIRST(MH)$，所以 S E L E C T ( S → M H ) = { F I R S T ( M H ) − ε } ∪ F O L L O W ( S ) = { # , b , e , d ， o } SELECT(S→MH)=\{FIRST(MH)-ε\}∪FOLLOW(S)=\{\#,b,e,d，o\} SELECT(S→MH)={FIRST(MH)−ε}∪FOLLOW(S)={#,b,e,d，o}，其中因为ε∈FIRST(M)，所以FIRST(MH)=FIRST(M)UFIRST(H)={b,d,e,ε}。
  ②求$SELECT(S\to a)$，$\epsilon \notin FIRST(a)$，所以 S E L E C T ( S → a ) = { F I R S T ( a ) − ε } = { a } SELECT(S→a)=\{FIRST(a)-ε\}=\{a\} SELECT(S→a)={FIRST(a)−ε}={a}
  ③求$SELECT(H\to LSo)$，$\epsilon \notin FIRST(LSo)$，所以 S E L E C T ( H → L S o ) = { e } SELECT(H→LSo)=\{e\} SELECT(H→LSo)={e}
  ④求$SELECT(H\to \epsilon )$，$\epsilon \in FIRST(\epsilon )$，所以 S E L E C T ( H → ε ) = F O L L O W ( H ) = { # , f , o } SELECT(H→ε)={FOLLOW(H)=\{\#,f,o\}} SELECT(H→ε)=FOLLOW(H)={#,f,o}
  ⑤求$SELECT(K\to dML)$，$\epsilon \notin FIRST(dML)$，所以 S E L E C T ( K → d M L ) = { d } SELECT(K\rightarrow{dML})=\{d\} SELECT(K→dML)={d}
  ⑥同理可求得： S E L E C T ( K → ε ) = { # , e , o } SELECT(K→ε)=\{\#,e,o\} SELECT(K→ε)={#,e,o}
  ⑦ S E L E C T ( L → e H f ) = { e } SELECT(L→eHf)=\{e\} SELECT(L→eHf)={e}
  ⑧ S E L E C T ( M → K ) = { # , d , e , o } SELECT(M→K)=\{\#,d,e,o\} SELECT(M→K)={#,d,e,o}
  ⑨ S E L E C T ( M → b L M ) = { b } SELECT(M→bLM)=\{b\} SELECT(M→bLM)={b}

  所以非终结符的SELECT集合表为：

  产生式	SELECT集合
  S→MH	{#,b,e,d,o}
  S→a	{a}
  H→LSo	{e}
  H→ε	{#,f,o}
  K→dML	{d}
  K→ε	{#,e,o}
  L→eHf	{e}
  M→K	{#,d,e,o}
  M→bLM	{b}

• Step5：求左部相同的产生式的SELECT集合的交集。
  从上表显然可知，左部相同的产生式的SELECT集合的交集都是空，故文法G[s]属于LL(1)文法。

……………………

参考文章：

• 编译原理-消除左递归
• LL(1)文法的判断
• 编译原理求FIRST集、FOLLOW集和SELECT集 （又发现一个大佬😆)

在此感谢所有CSDN乐于分享的博主