对称加密与非对称加密:密码学的基石及 RSA 算法详解
在当今数字化的时代,信息安全至关重要。对称加密和非对称加密作为密码学中的两种基本加密技术,为我们的数据安全提供了强大的保障。本文将深入探讨对称加密和非对称加密的特点、应用场景,以及详细介绍非对称加密算法中的 RSA 算法及其在 Java 中的实现和其他方面的应用。
一、对称加密与非对称加密概述
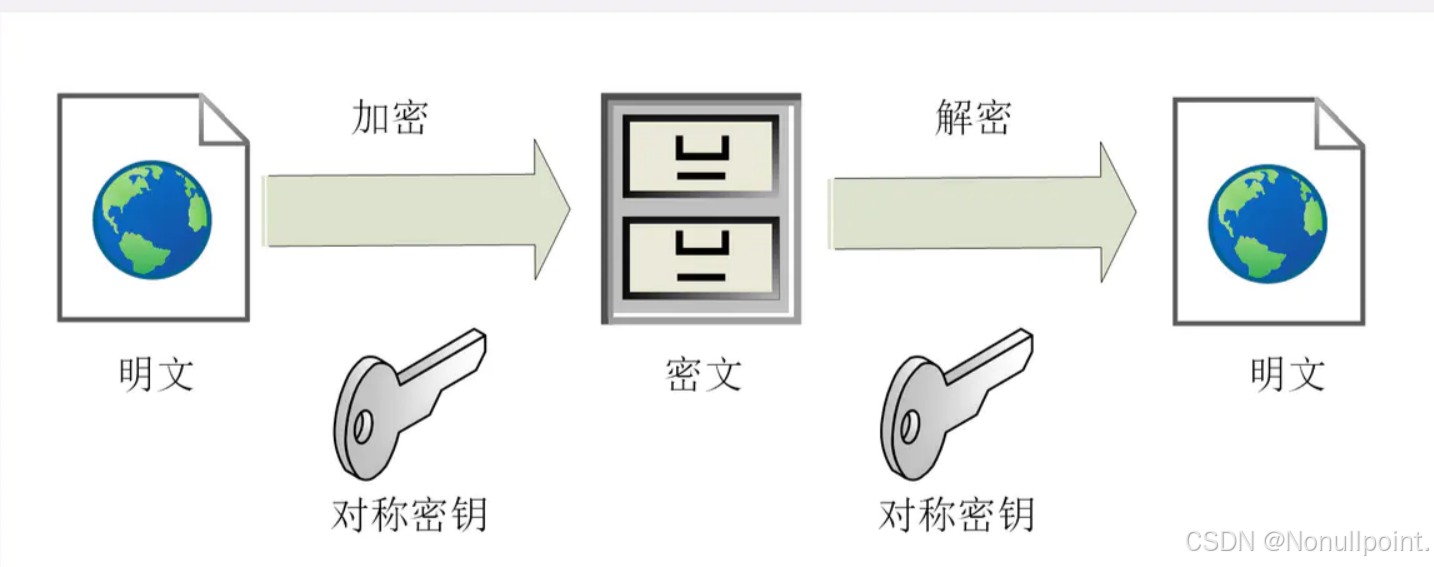
(一)对称加密
- 特点
- 高效性:使用相同的密钥进行加密和解密,速度较快,适用于加密大量数据。
- 密钥管理挑战:密钥的安全分发是一个主要问题。如果密钥被第三方截获,加密信息可能被破解,因此密钥的安全传递和保护至关重要。
- 常见算法:DES、AES、RC4、Blowfish 等。
- 应用场景:适用于加密存储在硬盘上的文件、数据库加密等需要高速加密大量数据的场景。
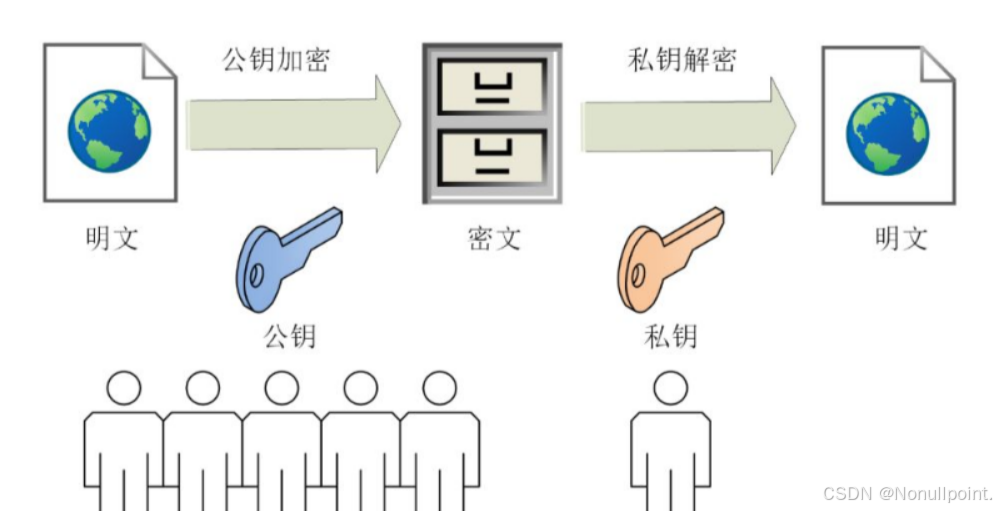
(二)非对称加密
- 特点
- 安全性高:使用一对密钥,公钥公开用于加密信息,私钥保密用于解密信息。私钥不需要在网络上传输,减少了被截获的风险。
- 计算开销大、速度慢:相比于对称加密,非对称加密的计算开销较大,速度较慢,通常不用于大量数据的直接加密。
- 简化密钥管理:公钥可以公开,私钥保持秘密,解决了对称加密中密钥分发的难题。
- 常见算法:RSA、DSA、ECC 等。
- 应用场景:适用于需要安全通信但难以安全地分发密钥的场景,如 HTTPS 通信、数字签名、加密电子邮件等。
二、RSA 非对称加密算法详解
(一)RSA 算法的起源
RSA 是非对称加密算法的一种,它的名字来源于三位发明者的名字首字母 ——Ron Rivest、Adi Shamir 和 Leonard Adleman。
(二)RSA 算法的安全性原理
RSA 算法的安全性基于大整数分解问题的难度。对于两个大素数的乘积,分解它们回到原来的素数是非常困难的,尤其是在没有足够计算资源的情况下。
下面是使用Markdown语法对RSA算法的详细解释:
密钥生成:
选择两个大的随机素数( p )和( q )。
计算它们的乘积( n = pq ),( n )的长度通常在1024到4096比特之间。
计算欧拉函数( \phi(n) = (p-1)(q-1) )。
选择一个整数( e ),满足( 1 < e < \phi(n) )并且( e )和( \phi(n) )互质。
计算( d ),使得( ed \equiv 1 \pmod{\phi(n)} )。换句话说,找到( d )使得( ed - 1 )是( \phi(n) )的倍数。
公钥是( (n, e) ),私钥是( (n, d) )。
加密过程:
假设要加密的消息( m )是一个小于( n )的整数。
使用公钥( (n, e) )加密消息( m )得到密文( c ):( c = m^e \mod n )。
解密过程:
使用私钥( (n, d) )解密密文( c )得到原始消息( m ):( m = c^d \mod n )。
RSA算法之所以有效,是因为( m^{ed} \equiv m \pmod{n} )。这是因为( ed \equiv 1 \pmod{\phi(n)} ),所以( m^{ed} )实际上等于( m )加上( \phi(n) )的倍数,这确保了在模( n )意义下,( m^{ed} )和( m )是相同的。
RSA的安全性依赖于大整数分解问题的难度,即给定( n ),很难找到( p )和( q )。然而,随着量子计算机的发展,使用Shor’s算法可以在多项式时间内解决大整数分解问题,从而威胁到RSA的安全性。因此,对于未来的安全考虑,正在研究和采用后量子加密算法。
需要注意的是,实际应用中,RSA通常不会直接用于大量数据的加密,因为其加密速度较慢。相反,它常被用于加密对称密钥,然后使用对称密钥加密大量数据,这种方法称为混合加密。
(三)RSA算法的使用:
在Java中,RSA非对称加密算法可以通过Java Cryptography Extension (JCE) API来实现。JCE提供了加密、解密、签名以及验证签名的功能。以下是在Java中使用RSA的基本步骤和示例代码:
步骤1: 生成密钥对
首先,你需要生成一个RSA密钥对,包括公钥和私钥。这通常通过KeyPairGenerator类完成。
import java.security.KeyPair;
import java.security.KeyPairGenerator;
import java.security.NoSuchAlgorithmException;
public class RSADemo {
public static void main(String[] args) {
try {
KeyPairGenerator keyGen = KeyPairGenerator.getInstance("RSA");
keyGen.initialize(2048); // 设置密钥长度,例如2048位
KeyPair keyPair = keyGen.generateKeyPair();
// 获取公钥和私钥
java.security.PublicKey publicKey = keyPair.getPublic();
java.security.PrivateKey privateKey = keyPair.getPrivate();
} catch (NoSuchAlgorithmException e) {
e.printStackTrace();
}
}
}
步骤2: 加密数据
使用公钥加密数据,这通常通过Cipher类完成。
import javax.crypto.Cipher;
import java.security.NoSuchPaddingException;
import java.security.InvalidKeyException;
import java.security.PublicKey;
public class RSADemo {
// 假设你已经有了publicKey和privateKey
private static PublicKey publicKey;
private static java.security.PrivateKey privateKey;
public static byte[] encryptData(byte[] data, PublicKey publicKey) {
try {
Cipher cipher = Cipher.getInstance("RSA/ECB/PKCS1Padding");
cipher.init(Cipher.ENCRYPT_MODE, publicKey);
return cipher.doFinal(data);
} catch (Exception e) {
e.printStackTrace();
return null;
}
}
}
步骤3: 解密数据
使用私钥解密数据,同样使用Cipher类。
public class RSADemo2 {
// 假设你已经有了publicKey和privateKey
private static PublicKey publicKey;
private static java.security.PrivateKey privateKey;
public static byte[] decryptData(byte[] encryptedData, java.security.PrivateKey privateKey) {
try {
Cipher cipher = Cipher.getInstance("RSA/ECB/PKCS1Padding");
cipher.init(Cipher.DECRYPT_MODE, privateKey);
return cipher.doFinal(encryptedData);
} catch (Exception e) {
e.printStackTrace();
return null;
}
}
}
注意事项:
- RSA 加密的数据大小有限制,一般不超过密钥长度减去一些开销。
- 在实际应用中,RSA 通常用于加密对称密钥而不是直接加密大量数据,后者通过更高效的对称加密算法如 AES 完成。
- 为了提高安全性,建议使用更长的密钥长度,比如 4096 位。
四、RSA 算法的其他应用
(一)数字签名
RSA 可以用于创建数字签名,通过私钥加密一小段数据(通常是消息摘要)来实现。任何人都可以使用与私钥相对应的公钥来验证签名的真实性,确保了数据的完整性和来源的认证。
(二)安全通信
在通信双方之间建立安全通道,例如在 TLS/SSL 协议中,公钥可以用来加密对称密钥,然后这个对称密钥用于加密会话中的数据,结合了非对称和对称加密的优点。
(三)密钥交换
用于安全地交换对称加密密钥。例如,在 Diffie-Hellman 密钥交换中,可以使用 RSA 作为额外的安全层来保护密钥。
(四)身份验证
在 SSH 协议中,客户端使用其私钥证明其身份给服务器端,而服务器使用存储的公钥来验证签名。
(五)软件分发
软件开发商可以使用 RSA 签名来签署其软件,用户可以确认软件的来源和完整性,防止恶意篡改。
(六)证书管理
在 PKI(公钥基础设施)中,RSA 用于创建和验证数字证书,这些证书包含公钥,并由信任的第三方(证书颁发机构)签名,以保证公钥属于特定实体。
(七)安全存储
用于加密存储在硬盘、USB 驱动器或其他存储介质上的敏感数据,确保即使物理介质被盗也无法访问数据。
(八)法律和合规性
在某些行业和法规中,RSA 签名可以用于确保合同和其他法律文件的电子版本具有法律效力。
(九)区块链和加密货币
在区块链技术中,RSA 或类似的非对称加密技术用于创建和验证交易签名,确保交易的有效性和不可篡改性。
(十)云服务安全
在云环境中,RSA 可以用于保护客户数据的隐私,确保只有授权用户才能访问加密数据。
由于 RSA 算法的计算成本较高,它通常用于加密较小的数据量,如密钥、签名或简短的信息,而对于大量数据则使用对称加密算法,同时使用 RSA 加密对称密钥。
技术中,RSA 或类似的非对称加密技术用于创建和验证交易签名,确保交易的有效性和不可篡改性。
(十)云服务安全
在云环境中,RSA 可以用于保护客户数据的隐私,确保只有授权用户才能访问加密数据。
由于 RSA 算法的计算成本较高,它通常用于加密较小的数据量,如密钥、签名或简短的信息,而对于大量数据则使用对称加密算法,同时使用 RSA 加密对称密钥。
总之,对称加密和非对称加密在信息安全领域都有着重要的地位,而 RSA 非对称加密算法作为其中的代表,在多个方面发挥着关键作用。了解和正确应用这些加密技术,对于保护我们的数字资产和信息安全至关重要。