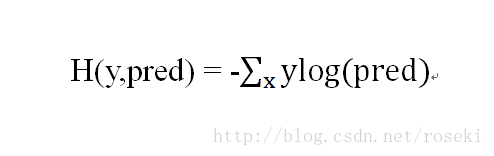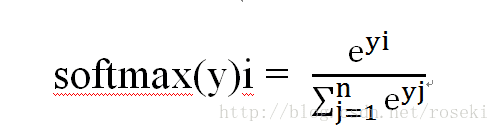白话TensorFlow+实战系列(三)
常用损失函数以及参数优化
这次主要介绍常用损失函数以及关于神经网络优化的问题
1.常用损失函数:
神经网络解决的现实问题主要有两大类:分类与回归。分类指的是将未知数据归类到你希望的类别中去,如经典的mnist识别手写数字,就是将图片分类到0~9中。回归问题一般是拟合一个具体的数据,如预测房价与房屋面积、单价的关系。下面就从这两方面列举常用的损失函数。
分类问题:
分类问题中,因为是将数据分成有限类,因此自然而然想到的就是通过概率来判断属于哪一类,概率最大的就是结果。针对概率,一般是用交叉熵来作损失函数,交叉熵刻画的是两个概率分布之间的距离。其方程如下:
其中y为真实数据的概率分布(如[1,0,0]表示三分类中的第一类,可看成概率分布),pred为神经网络输出的概率分布。
然而全连接神经网络的输出并非是一个概率分布,因此需要人为的对输出进行进一步的处理,即所谓的softmax层。他的作用是将网络的输出全部压缩至0-1之间,并且和为1,因此可以将其输出看做概率分布。其公式如下:
如网络输出为[1,0,0],经过softmax层后变为[e/e+2,1/e+2, 1/e+2],这样就将输出变成概率分布,随后可由交叉熵做损失函数了。
在TensorFlow中,tf.nn.softmax_cross_entropy_with_logits(pred,y)集成了上面的步骤,即先经过softmax层然后进行交叉熵的计算。示例代码如下:
回归问题:
回归问题是对具体数值的预测,即预测的是任意实数。对于回归问题,最常用的是均方差损失函数,定义如下:
示例代码如下:
这就是两类问题常用的损失函数。当然这还远远不够,下面就讲讲网络优化的问题。
2.网络优化问题:
1)学习率
学习率(learning_rate)可理解为每一次梯度下降的步长,一般设置学习率小于0.1,具体多少其实算是一门玄学,全靠经验。当学习率过大时,可能导致参数在最低点附近来回震荡,始终到达不了最优点;当学习率过小时,前期梯度下降的速度极其慢,浪费时间。所以最优的方法是前期学习率设置大点,让梯度迅速下降,随后慢慢将学习率减小,以求达到最优点。
在TensorFlow中提供了类似的设置学习率方法——指数衰减法。用tf.train.exponential_decay实现。代码如下:
其中0.1为初始学习率;100表示每100轮学习率变一次,这个轮数是由total_data除以batch_size得到的,也可以理解为每一个epoch学习率变一次;0.98表示每次变化为上一次学习率乘以0.98;staircase= True表示成阶梯函数下降,False时表示连续衰减。
注意global_step在optimizer中的minimize中要引用。
2)过拟合
评价一个神经网络模型的好坏并非是由模型在训练数集中的表现来决定的,是由测试集说了算,即模型在预测未知数据的表现来决定。过拟合指的是模型在训练集中的表现非常好,甚至可以准确的分类每一个训练数据,然而这种模型在预测未知数据的时候表现并不好,模型过于复杂,即所谓的泛化能力不行。相反的即欠拟合,模型过于简单。如图:
第一个即为欠拟合,模型太简单了,分类效果不好
第二个为正确的模型。
第三个即过拟合,模型过于复杂,导致泛化能力不行。
针对过拟合的问题,有常见的两类方法,一个为dropout,另一个为正则化。
dropout :
dropout原理就是在每次训练的时候,通过随机概率让一些神经元不工作,已达到防止过拟合的目的。
实现dropout很简单,代码如下:
第一个为一般的dropout,常用于全连接层。其中x表示需要dropout的层,keep_prob表示保留的概率,如等于0.4表示随机档掉0.6的神经元。
第二个用于RNN网络中,具体后续会讲。
TensorFlow建议定义keep_prob的时候用placeholder,在run的时候传入,但也可以直接传入0.4,如tf.nn.dropout(x, keep_prob = 0.4)
正则化:
正则化的原理就是在损失函数中加入评价模型复杂度的指标:loss = j(Ɵ) + ƛR(w),其中j(Ɵ)为损失函数,他是所有参数的函数;R(w)就是评价模型复杂度的指标,一般只是权重w的函数,ƛ表示复杂损失在总损失中的比例。
常用的正则化有L1与L2两种方法,而在TensorFlow中,L1与L2方法都有集成的函数,分别为:
L1:tf.contrib.layers.l1_regularizer(lambda)(w)
L2:tf.contrib.layers.l2_regularizer(lambda)(w)
下面以L2举例
L2正则化的定义:
即所有权重的平方和。
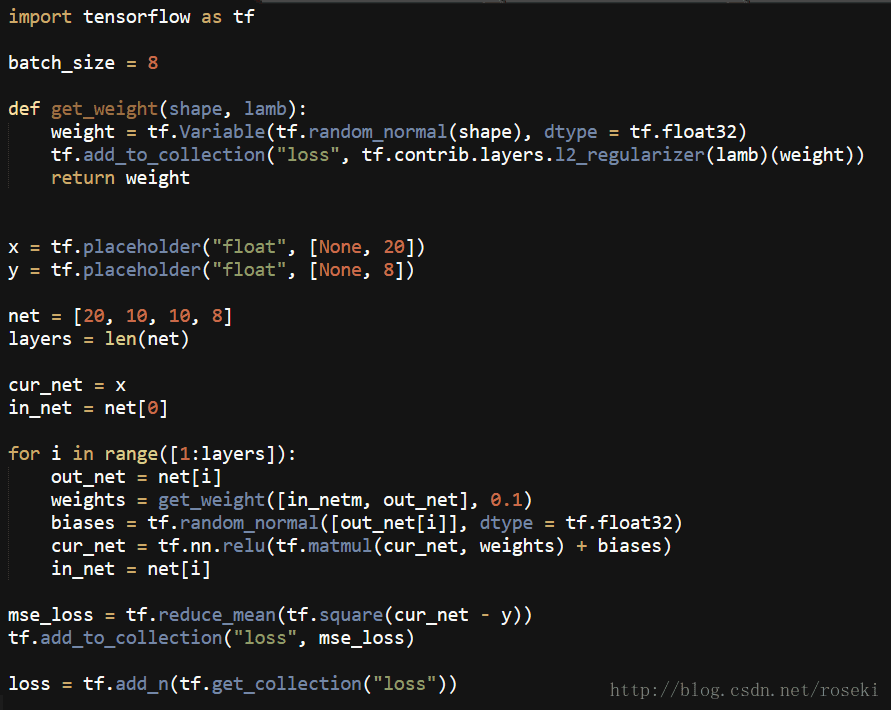
示例代码如下:
这是构建了一个[20,10,10,8]的全连接神经网络
其中get_weight函数用于获取每一层的权重w并进行L2正则化后放入collection中进行管理。
cur_net表示的是当前神经网络层。
in_net与out_net表示的是相邻的两层,用于构建权重。
for循环就是构建网络过程。
mse_loss就是均方差损失函数
最后一并加入collection中,全部相加就得到最后的loss。
滑动平均模型:
在采用随机梯度下降法对神经网络进行训练的时候,滑动平均模型能进一步的提高模型的准确率。TensorFlow中,tf.train.ExponentialMovingAverage用来实现该功能。其原理为:
该函数会为每一个变量生成一个影子变量(shadow_variable),影子变量的初始值即为变量的初始值,随后影子变量由该方程进行改变:
shadow_variable= decay * shadow_variable + (1 - decay) * variable
其中decay为衰减率,一般decay的设置为接近1的数。同时该函数还提供根据step来动态的设置decay:
min{ decay , 1+step / 10 + step}
具体使用案例会在以后进行说明。