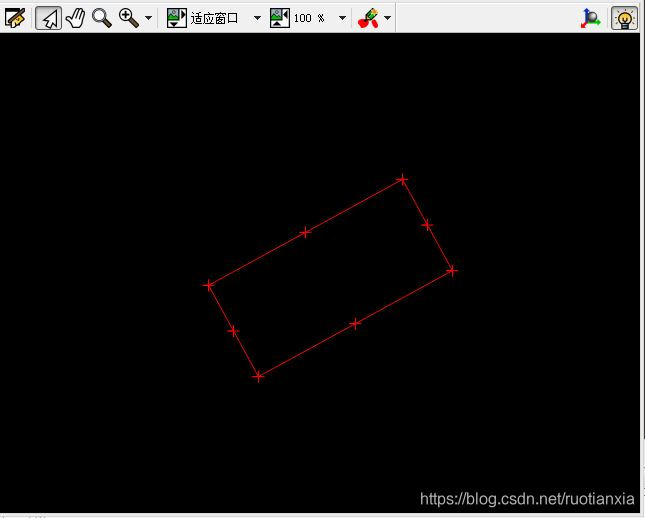
Halcon 工业应用实用教程中的一个例子:
* CenterY : 仿射矩形中心y
* CenterX: 仿射矩形中心x
* Phi: 仿射矩形角度
* Len1: 仿射矩形宽的一半
* Len2: 仿射矩形高的一半
* CornerY: 仿射矩形端点y
* CornerX: 仿射矩形端点x
* LineCenterY: 仿射矩形边中点y
* LineCenterx: 仿射矩形边中点x
* 矩形端点坐标、边中心坐标初始化
CornerY := []
CornerX := []
LineCenterY := []
LineCenterX := []
* 临时变量初始化
RowT := 0
ColT := 0
* 判断仿射矩形是否有效
if (Len1 <= 0 or Len2 <= 0)
return()
endif
* 计算仿射矩形的正弦值、余弦值
tuple_cos(Phi, Cos)
tuple_sin(Phi, Sin)
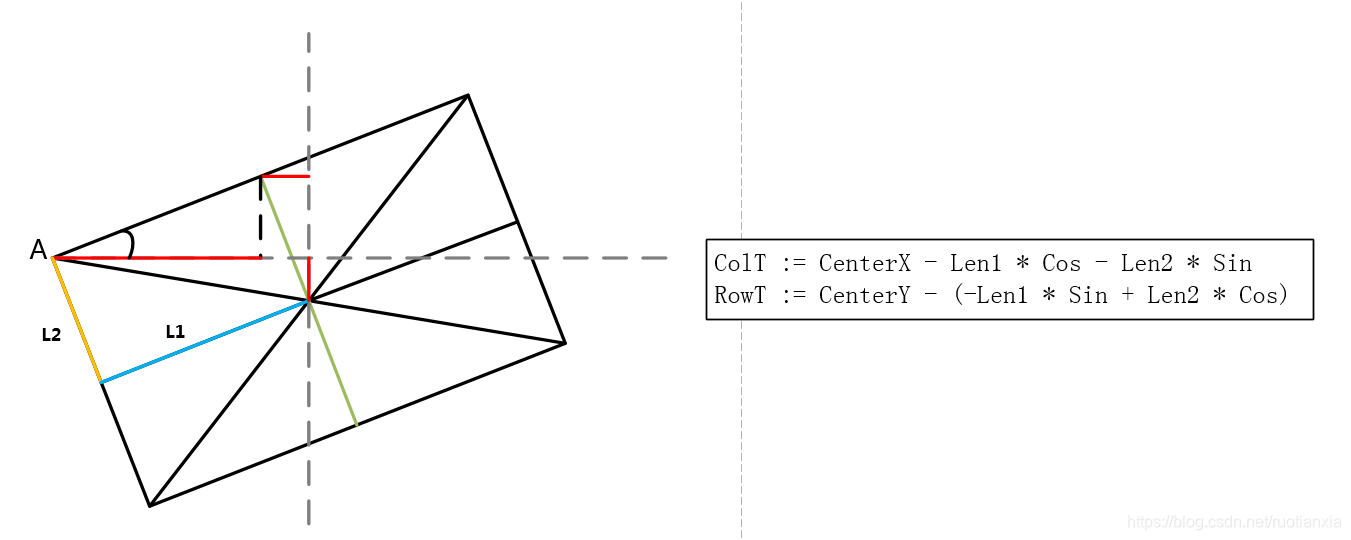
* 矩形第一个端点计算(左上)
ColT := CenterX - Len1 * Cos - Len2 * Sin
RowT := CenterY - (-Len1 * Sin + Len2 * Cos)
CornerY := [CornerY, RowT]
CornerX := [CornerX, ColT]
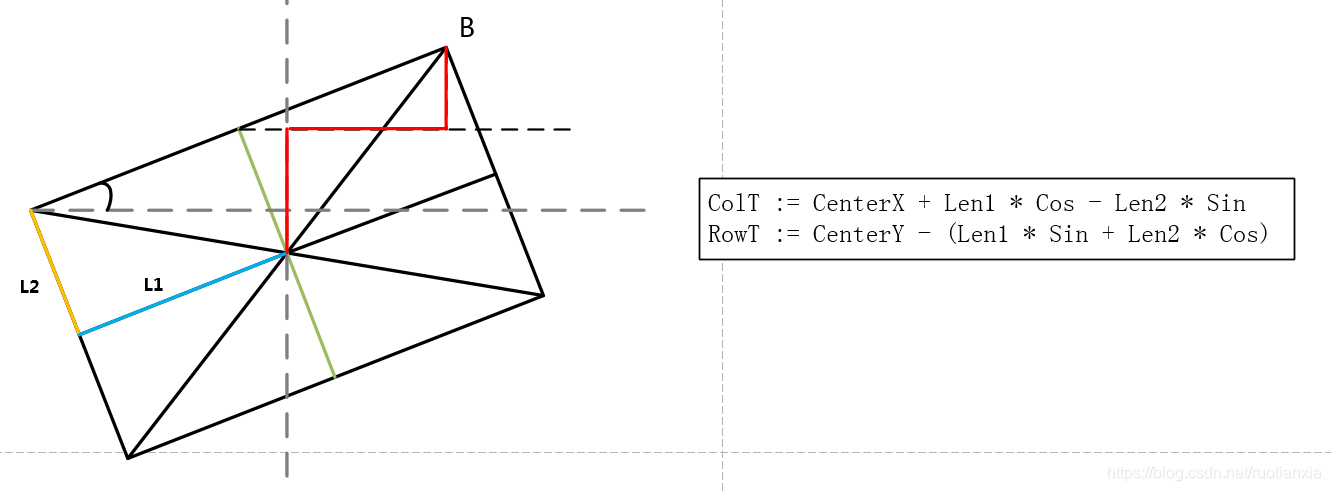
* 矩形第二个端点计算(右上)
ColT := CenterX + Len1 * Cos - Len2 * Sin
RowT := CenterY - (Len1 * Sin + Len2 * Cos)
CornerY := [CornerY, RowT]
CornerX := [CornerX, ColT]
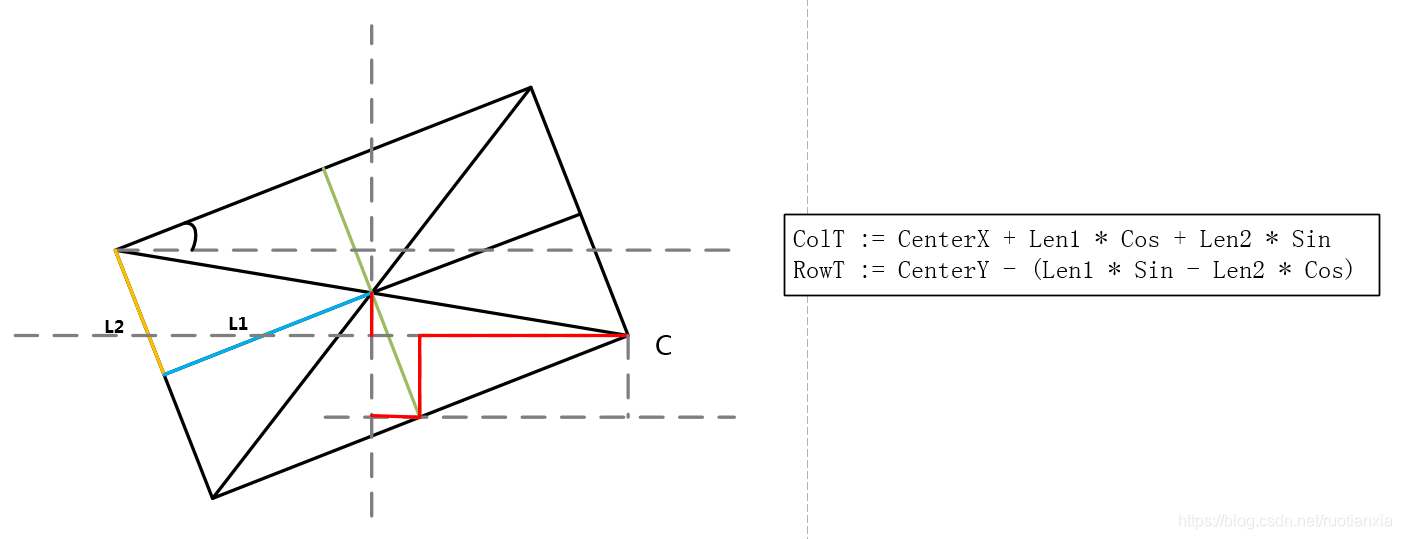
* 矩形第三个端点计算(右下)
ColT := CenterX + Len1 * Cos + Len2 * Sin
RowT := CenterY - (Len1 * Sin - Len2 * Cos)
CornerY := [CornerY, RowT]
CornerX := [CornerX, ColT]
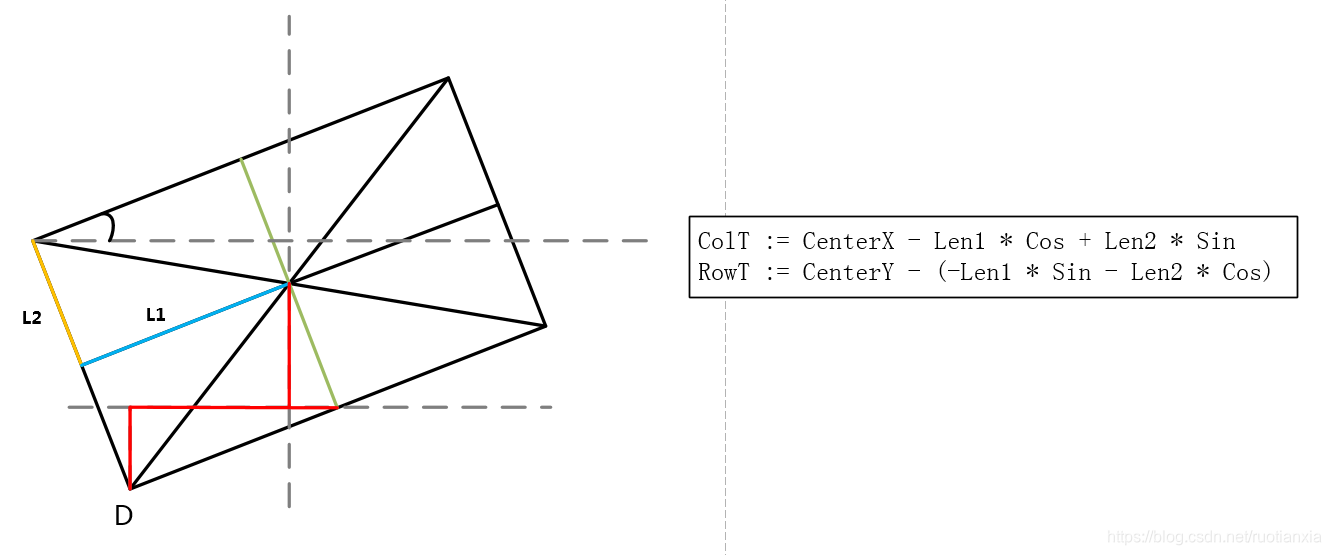
* 矩形的第四个端点计算(左下)
ColT := CenterX - Len1 * Cos + Len2 * Sin
RowT := CenterY - (-Len1 * Sin - Len2 * Cos)
CornerY := [CornerY, RowT]
CornerX := [CornerX, ColT]
* 矩形第一条边中心坐标(上边)
LineCenterY[0] := (CornerY[0] + CornerY[1]) * 0.5
LineCenterX[0] := (CornerX[0] + CornerX[1]) * 0.5
* 矩形第二条边中心坐标(右边)
LineCenterY[1] := (CornerY[1] + CornerY[2]) * 0.5
LineCenterX[1] := (CornerX[1] + CornerX[2]) * 0.5
* 矩形第三条边中心坐标(下边)
LineCenterY[2] := (CornerY[2] + CornerY[3]) * 0.5
LineCenterX[2] := (CornerX[2] + CornerX[3]) * 0.5
* 矩形第四条边中心坐标(左边)
LineCenterY[3] := (CornerY[3] + CornerY[0]) * 0.5
LineCenterX[3] := (CornerX[3] + CornerX[0]) * 0.5
return ()
结果s
最近有人说这个计算的原理错了(其实是书上的一段例程),我现将计算方式展示如下,若有错误之处,请指出!!!
(PS:在实际使用的过程中,会遇到顶点顺序的问题,所以加一个对坐标的判断即可)