A算法与D算法
1. A* (Informed Search)
1.1
Evaluation Function: f(n)=g(n)+h(n)
operating cost function: g(n)
Heuristic fucntion: h(n)
(相较于Dijkstra 算法 增加了启发式函数 来确定最优路径)
可用启发式函数:曼哈顿距离 欧式距离 对角距离
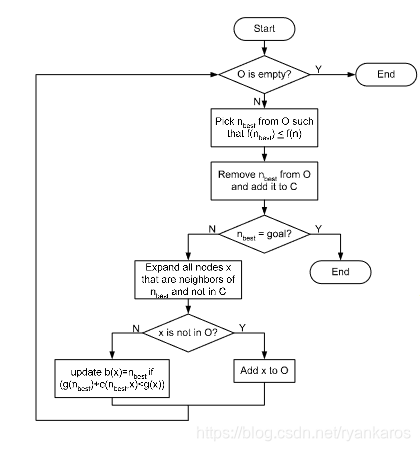
流程图如下图所示:
Open list: 存储扩展的节点
close list: 存储已经搜索过的节点
1.2 A*算法运行中需要注意的问题
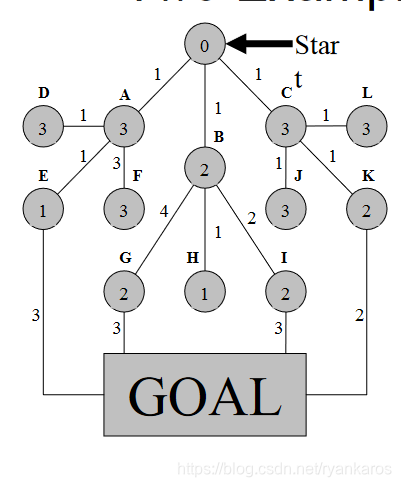
- 从root开始, 圆圈内表示该节点启发式函数数值,连线上表示代价函数数值
- 每一个节点的启发式函数是独立的,不与之前节点启发式函数大小相关
- 途中节点的代价函数数值总是由root 出发的代价函数总和
- 每一步搜索时将open list中f(n)最小的节点添加到close list 中,要注意close list中要带上f(n)值进行存储,以便于最终到达goal时判断最优路径
- close list中出现goal节点即为停止搜索flag
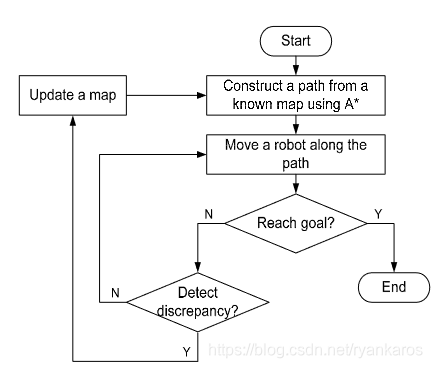
1.3 A* replanner (用于未知地图情况)
- 流程右半部分为正常A* 流程, 从ROOT出发在已知地图中进行搜索,判断是否到达GOAL
- 如果没有到达GOAL,则判断是否与一直地图存在差异
- 若与已知地图存在差异,则更新地图,并使用更新后地图继续搜索
- 若与已知地图没有差异,说明没有动态障碍物产生,继续按照原地图搜索
- 知道到达GOAL停止
2. D*算法 (Stentz 1994)
2.1 介绍
- 又称动态A搜索 (Dynamic A Search)
- 过程中节点间代价函数会发生改变 (replanning online)
- 等价于A* replanner
- 使用Dijkstra 进行初始规划,并通过接受实时数据来加快规划速度,针对部分地图区域来实现动态避障
- 比A* replanner 更高效 (大范围复杂环境扩展中)
- 用于在第一次逆向搜索获得最优路径并记录节点间关系后,处理动态问题
- h:到GOAL代价 k:该点最小的h
- 使用k原因:k用于open list排序,说明此节点之前为最优节点,可在此节点周围进行搜索,加快重新规划的速度

- 初始阶段,所有节点均为NEW(代表第一次遍历到),h和k值均为到GOAL的距离
- 从GOAL出发,将GOAL添加到open list中,且它的h=0 k=0 (k值为队列中优先度)
- 将GOAL pop出open list,扩展到GOAL的相邻节点,因为此时节点均为NEW,所以k=h=到GOAL的距离,将相邻节点推入open list中
- 不停寻找相邻节点,迭代,推入推出open list
- !!!若此时遇到节点处为障碍物,此节点h值很高,因为为NEW,所以k=h=high value
- 当root被扩展后,则搜索结束
- 根据h的梯度确定最优路径 (方向指向临间节点中k值最小的节点)
- !!当计划路径上某点被阻碍,因为是反向指针,可以定位到被堵节点的上一节点(D*速度快的原因)
- 障碍物节点h升高,RISE态,需搜索使得该点的h降低,回复lower state
- 将该障碍点和临间节点加入open list中,进行搜索,如果无法使该点转为lower态,说明临间通过节点无法成功绕开障碍物,则将该影响扩散
- 该点的子节点受到影响,h变大,并进行判断
- 若 k_old<h(x): 该节点x处于raise状态,如果在x周围找到一个临间节点,使得h.y+c(x,y)更小,那就修改x的父节点,重置其h的值(父节点h+节点间距离)。
- 若k_old=h(x): 该节点x处于lower的状态,并没有受到障碍影响,或者还在第一遍遍历的阶段。