前面介绍了《粒子群算法》的基本原理，这里结合实例，看看粒子群算法是怎样解决实际问题的。采用过的函数和《遗传算法实例》中的一样：

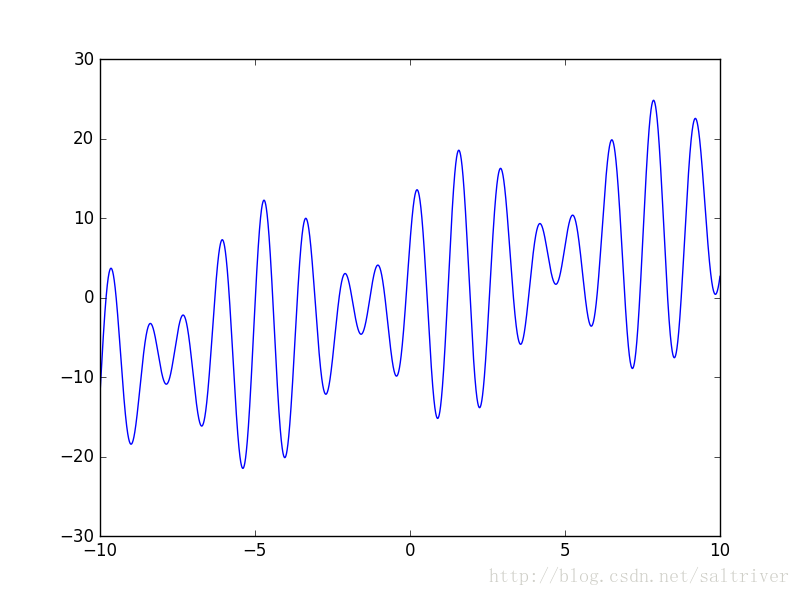
求其在区间[-10,10]之间的最大值。下面是该函数的图像：

在本例中，我们可以把x作为个体的染色体，函数值f(x)作为其适应度值，适应度越大，个体越优秀，最大的适应度就是我们要求的最大值。
直接看代码吧（直接看注释就能看懂）。

# -*- coding: utf-8 -*-

import numpy as np

# 粒子（鸟）
class particle:
    def __init__(self):
        self.pos = 0  # 粒子当前位置
        self.speed = 0
        self.pbest = 0  # 粒子历史最好位置


class PSO:
    def __init__(self):
        self.w = 0.5  # 惯性因子
        self.c1 = 1  # 自我认知学习因子
        self.c2 = 1  # 社会认知学习因子
        self.gbest = 0  # 种群当前最好位置
        self.N = 20  # 种群中粒子数量
        self.POP = []  # 种群
        self.iter_N = 100  # 迭代次数

    # 适应度值计算函数
    def fitness(self, x):
        return x + 10 * np.sin(5 * x) + 7 * np.cos(4 * x)

    # 找到全局最优解
    def g_best(self, pop):
        for bird in pop:
            if bird.fitness > self.fitness(self.gbest):
                self.gbest = bird.pos

    # 初始化种群
    def initPopulation(self, pop, N):
        for i in range(N):
            bird = particle()
            bird.pos = np.random.uniform(-10, 10)
            bird.fitness = self.fitness(bird.pos)
            bird.pbest = bird.fitness
            pop.append(bird)

        # 找到种群中的最优位置
        self.g_best(pop)

    # 更新速度和位置
    def update(self, pop):
        for bird in pop:
            # 速度更新
            speed = self.w * bird.speed + self.c1 * np.random.random() * (
                bird.pbest - bird.pos) + self.c2 * np.random.random() * (
                self.gbest - bird.pos)

            # 位置更新
            pos = bird.pos + speed

            if -10 < pos < 10: # 必须在搜索空间内
                bird.pos = pos
                bird.speed = speed
                # 更新适应度
                bird.fitness = self.fitness(bird.pos)

                # 是否需要更新本粒子历史最好位置
                if bird.fitness > self.fitness(bird.pbest):
                    bird.pbest = bird.pos

    # 最终执行
    def implement(self):
        # 初始化种群
        self.initPopulation(self.POP, self.N)

        # 迭代
        for i in range(self.iter_N):
            # 更新速度和位置
            self.update(self.POP)
            # 更新种群中最好位置
            self.g_best(self.POP)


pso = PSO()
pso.implement()

for ind in pso.POP:
    print("x=", ind.pos, "f(x)=", ind.fitness)

某一次执行中生成的种群结果：
x= 7.44390041845 f(x)= 2.34326279816
x= 9.48378207609 f(x)= 13.3821268397
x= 6.3672261374 f(x)= 17.0548851104
x= 7.85674414126 f(x)= 24.855362869
x= 7.85674414216 f(x)= 24.855362869
x= 7.85674414201 f(x)= 24.855362869
x= 7.85674414185 f(x)= 24.855362869
x= 8.02319542929 f(x)= 20.1093330013
x= 7.85674414327 f(x)= 24.855362869
x= 7.85674414414 f(x)= 24.855362869
x= 7.85674414288 f(x)= 24.855362869
x= 7.85674414296 f(x)= 24.855362869
x= 7.85674414178 f(x)= 24.855362869
x= 7.85674414174 f(x)= 24.855362869
x= 7.8567441494 f(x)= 24.855362869
x= 6.44588532539 f(x)= 19.2820411821
x= 7.85674414041 f(x)= 24.855362869
x= 9.93067628809 f(x)= 1.12241685006
x= 7.8567441425 f(x)= 24.855362869
x= 8.81867117742 f(x)= 4.6512749143
得到的最优解结果为：
X=7.85674414174 f(x)=24.855362869
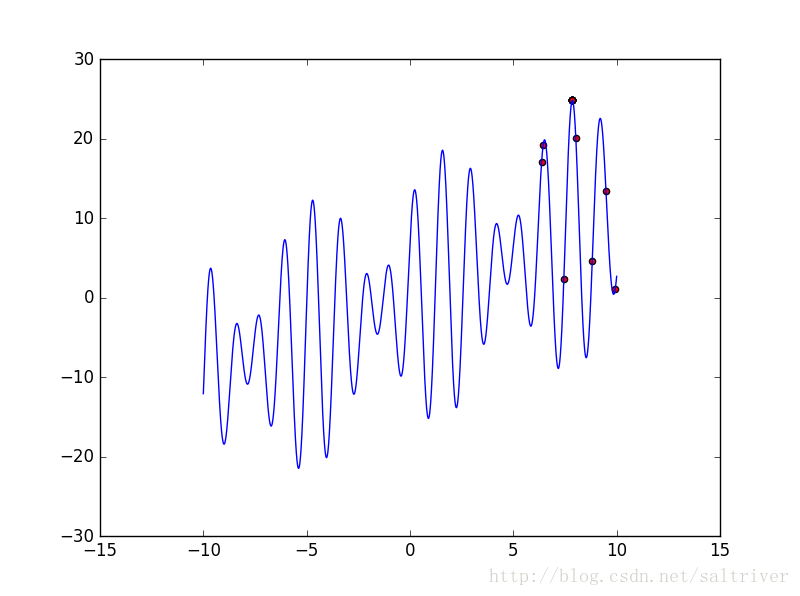
从图像上看符合要求。其结果图像如下，红色点表示种群中个体的位置。

# 绘图代码
import matplotlib.pyplot as plt
def func(x):
    return x + 10 * np.sin(5 * x) + 7 * np.cos(4 * x)

x = np.linspace(-10, 10, 10000)
y = func(x)

scatter_x = np.array([ind.pos for ind in pso.POP])
scatter_y = np.array([ind.fitness for ind in pso.POP])
plt.plot(x, y)
plt.scatter(scatter_x, scatter_y, c='r')
plt.show()