求素数的个数（三种方法）

1、实验目的与基本要求：
熟悉素数的判定及算法的优化。

2、实验内容：
求2~n素数的个数。
操作菜单要求：
输入n，输出2~n素数的个数。
该实验内容以“long”作为数据元素n的数据类型即可。

#include <stdio.h>
#include <math.h>
#include <time.h>
#include <string.h>


bool prime(long n);
void primeTime(long a);

void AiShi(long b); 

void Oula(long c);

int main()
{
	long long int n;
	printf("素数：输入n的值：");
	scanf("%ld",&n);
	AiShi(n);
	Oula(n);
	prime(n);
	primeTime(n);
	
	return 0;
}

埃氏筛选法实现思路：首先，需要一个存储素数的数组和一个筛选是否为素数的数组，数组存储21052375个数，其中元素的值为0（代表素数）。由于最小的数字2是素数。将表中2的倍数都划去，当然也包括其本身，（即筛选数组的元素值为1，代表合数）。以此类推，每次表中剩下的最小数字m都是素数，然后将表中所有的m的倍数划去。如此反复操作，便能筛出n以内的所有素数。

const int x = 21000000;
bool shaixuan[x];	//筛选 是否为素数的数组  1为合数 0为素数 
int sushu[x];		//创建存取素数的数组 

void AiShi(long b)
{
	clock_t t3;
	t3 = clock();
	int count = 0; 
	for(long i = 2; i <= b; i++)
	{
		if(shaixuan[i] == 0)				// 默认为 0 -> 素数 
		{
			sushu[++count] = i;			
			for(long j = 2; j <= b / i; j++)
			{
				if(i * j >= b)
				{
					break;
				}
				else
				{
					shaixuan[i * j] = 1;		// 1 代表都是素数的倍数(合数)->不是素数 
				}
			}
		}	
	}
	
	clock_t t4;
	t4 = clock() - t3;
	
	printf("方法2:\n");
	printf(" 结果：2到%ld的素数个数为：%ld\n",b,count-1);
	printf(" 用时：%lf秒\n",(float)t3/CLOCKS_PER_SEC);	
		
} 

欧拉筛选法实现思路：此算法是在埃氏算法的基础上多了判断的步骤，从而消去了这种重复标记的情况，思路是用合数中的一个因数筛掉这个合数。具体的实现方式是利用已经求得的素数，第一重循环将区间内的数从小到大遍历，第二重循环将已求得的素数从小到大遍历，将这个数和素数的乘积标记为合数。如果一个数能被素数整除，跳出循环。如此反复操作，便能筛出n以内的所有素数。

#define yxx 21000000

bool shaixuan2[yxx];			//筛选 是否为素数的数组 
int sushu2[yxx];				//创建存取素数的数组
int num = 0;				//素数个数 


void Oula(long c)
{
	int count = 0;
	
	clock_t t5;
	t5 = clock();
	
	//0标记不是素数，1标记是素数 
    memset(shaixuan2,1,sizeof(shaixuan2));		//shaixuan素数所有元素标记 1 
    shaixuan2[0] = shaixuan2[1] = 0;				//下标为0和1的元素(0/1)不是素数，标记 0				
    for(int i = 2;i <= yxx;i++)
    {
        if(shaixuan2[i])
        {
        	sushu2[++count] = i;
		}
        for(int j = 1; j <= count && i * sushu2[j] <= yxx;j++)	//合数在给定范围内
        {
            shaixuan2[i * sushu2[j]] = 0;
            if(i % sushu2[j] == 0)
            {
            	break;
			}       
        }
    }
    
    clock_t t6;
	t6 = clock() - t5;
    
    printf("方法3:\n");
    printf(" 结果：2到%ld的素数个数为：%ld\n",c,count);
	printf(" 用时：%lf秒\n",(float)t5/CLOCKS_PER_SEC);
}

暴力法：也就是循环2~n个数字判断是素数就返回，不是素数就继续下一个数接着判断。

bool prime(long n)
{
	for(long i = 2; i <= (long)sqrt(n); i++)
	{
		if(n % i == 0)
		{
			return 0;
		}
	}
	return 1;
}

void primeTime(long a)
{
	clock_t t1;
    long count = 0;
	t1 = clock();
	for(long j = 2; j <= a; j++)
	{
		if(prime(j))
		{
			count++;
		}
	}
	
	clock_t t2;
	t2 = clock() - t1;
	
	printf("方法1:\n");
	printf(" 结果：2到%ld的素数个数为：%ld\n",a,count);
	printf(" 用时：%lf秒\n",(float)t1/CLOCKS_PER_SEC);
	
}

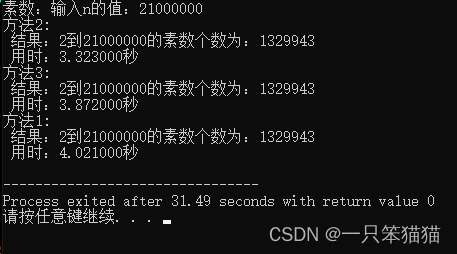
运行结果（方法1：暴力法，方法2：埃氏筛选法，方法3：欧拉筛选法）