1. z 变换

单位脉冲响应为 $h[n]$ 的离散时间线性时不变系统对复指数输入 $z^n$ 的响应 $y[n]$ 为

$$y[n]=H(z)z^n\text{\hspace{1em}(1)}$$

式中 $H(z)$ 是一个复常数，为

$$H[z]=\sum _{n=-\infty }^{+\infty }h[n]z^{-n}\text{\hspace{1em}(2)}$$

若 $z=e^{j\omega }$，这里 $\omega$ 为实数（即，$|z|=1$），则（2）式的求和式就是 $h[n]$ 的离散时间傅里叶变换。在更为一般的情况下，当 $|z|$ 不限制为 1 的时候，（2）式就称为 $h[n]$ 的 $z$ 变换。

一个离散时间信号 $x[n]$ 的 $z$ 变换定义为

$$\boxed{X(z)\stackrel{△}{=}\sum _{n=-\infty }^{+\infty }x[n]z^{-n}}\text{\hspace{1em}(3)}$$

若将复变量 $z$ 表示成极坐标形式

$$z=r{e}^{j\omega }\text{\hspace{1em}(4)}$$

用 $r$ 表示 $z$ 的模，而用 $\omega$ 表示它的相角。利用 $r$ 和 $\omega$，（3）式就变为

(5) X ( r e j ω ) = ∑ n = − ∞ + ∞ x [ n ] ( r e j ω ) − n = ∑ n = − ∞ + ∞ { x [ n ] r − n } e − j ω n \tag 5 X(r e^{j\omega}) =\sum_{n=-\infty}^{+\infty}x[n](r e^{j\omega})^{-n} = \sum_{n=-\infty}^{+\infty}\{x[n]r^{-n}\} e^{-j\omega n} X(rejω)=n=−∞∑+∞​x[n](rejω)−n=n=−∞∑+∞​{x[n]r−n}e−jωn(5)

由此可见，$X(r{e}^{j\omega })$ 就是序列 $x[n]$ 乘以实指数 $r^{-n}$ 后的傅里叶变换，即

(6) X ( r e j ω ) = F { x [ n ] r − n } \tag 6 X(r e^{j\omega}) =\displaystyle \mathcal F\{x[n]r^{-n}\} X(rejω)=F{x[n]r−n}(6)

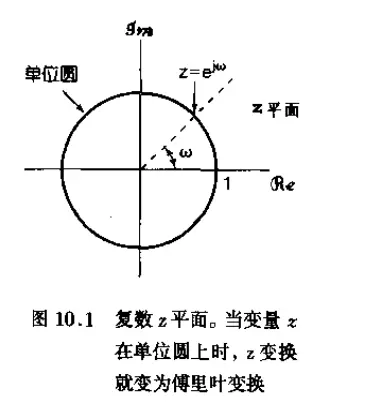
在 $z$ 变换中当变换变量 $z$ 的模为 1 时，即 $z=e^{j\omega }$，$z$ 变换就演变为傅里叶变换。于是，傅里叶变换就成为在复数 $z$ 平面中，半径为 1 的圆上的 $z$ 变换。在 $z$ 平面上，这个圆称为单位圆。

一般来说，对于某一序列的 $z$ 变换，存在着某一个 $z$ 值的范围，对该范围内的 $z$，$X(z)$ 收敛，这样一些值的范围就称为收敛域（ROC）。如果 ROC 包括单位圆，则傅里叶变换也收敛。

• 例 1
  

• 例 2
  

2. $z$ 变换的收敛域

性质 1：$X(z)$ 的 $ROC$ 是在 $z$ 平面上以原点为中心的圆环。

性质 2：$ROC$ 内不包含任何极点。

性质 3：如果 $x[n]$ 是有限长序列，那么 $ROC$ 就是整个 $z$ 平面，可能除去 $z=0$ 和/或 $z=\infty$。

性质 4：如果 $x[n]$ 是一个右边序列，并且 $|z|=r_0$ 的圆位于 $ROC$ 内，那么 $|z|>r_0$ 的全部有限 $z$ 值都一定在这个 $ROC$ 内。

性质 5：如果 $x[n]$ 是一个左边序列，并且 $|z|=r_0$ 的圆位于 $ROC$ 内，那么 $ 0< |z| < r_0$ 的全部 $z$ 值都一定在这个 $ROC$ 内。

性质 6：如果 $x[n]$ 是双边序列，并且 $|z|=r_0$ 的圆位于 $ROC$ 内，那么该 $ROC$ 一定是由包括 $|z|=r_0$ 的圆环所组成。

性质 7：如果 $x[n]$ 的 $z$ 变换 $X(z)$ 是有理的，那么它的 $ROC$ 就被极点所界定，或者延伸到无限远。

性质 8：如果 $x[n]$ 的 $z$ 变换 $X(z)$ 是有理的，而且若 $x[n]$ 是右边序列，那么，$ROC$ 就位于 $z$ 平面内最外层极点的外边；也就是半径等于 $X(z)$ 极点中最大模值的圆的外边。而且，若 $x[n]$ 是因果序列（即 $x[n]$ 为 $n<0$ 等于 $0$ 的右边序列），那么，$ROC$ 也包括 $z=\infty$。

性质 9：如果 $x[n]$ 的 $z$ 变换 $X(z)$ 是有理的，而且若 $x[n]$ 是左边序列，那么，$ROC$ 就位于 $z$ 平面内最里层的非零极点的里边；也就是半径等于 $X(z)$ 中除去 $z=0$ 的极点中最小模值的圆的里边，并且向内延伸到可能包括 $z=0$。特别地，若 $x[n]$ 是反因果序列（即 $x[n]$ 为 $n>0$ 等于 $0$ 的左边序列），那么，$ROC$ 也包括 $z=0$。

3. $z$ 反变换

对（6）式两边进行傅里叶反变换可得

$${\mathcal{F}}^{-1}X(r{e}^{j\omega })=x[n]r^{-n}\text{\hspace{1em}(7)}$$

因此

$$x[n]=r^n{\mathcal{F}}^{-1}X(r{e}^{j\omega })=r^n\frac{1}{2\pi }{\int }_{2\pi }X(r{e}^{j\omega })e^{j\omega n}d\omega \text{\hspace{1em}(8)}$$

将 $r^n$ 的指数因子移进积分号内，则有

$$x[n]=\frac{1}{2\pi }{\int }_{2\pi }X(r{e}^{j\omega })(r{e}^{j\omega }{)}^{n}d\omega \text{\hspace{1em}(9)}$$

也就是说，将 $z$ 变换沿着在 $ROC$ 内 $z=r{e}^{j\omega }$，$r$ 固定而 $\omega$ 在一个 $2\pi$ 区间内变化的闭合围线上求值，就能将 $x[n]$ 恢复出来。

现在将积分变量从 $\omega$ 改为 $z$。由于 $z=r{e}^{j\omega }$，$r$ 固定，$dz=jr{e}^{j\omega }d\omega =jzd\omega$，或者 $d\omega =(1/j)z^{-1}dz$。这样，（9）式中在 $\omega$ 的 $2\pi$ 区间的积分，利用 $z$ 以后，就对应于变量 $z$ 在环绕 $|z|=r$ 的圆上一周的积分。

$$x[n]=\frac{1}{2\pi j}\oint X(z)z^{n-1}dz\text{\hspace{1em}(10)}$$

式中，$\oint$ 记为在半径为 $r$，以原点为中心的封闭圆上沿逆时针方向环绕一周的积分。$r$ 的值可选为使 $X(z)$ 收敛的任何值，也就是使 $|z|=r$ 的积分围线位于 $ROC$ 的任何值。

• 确定 $z$ 反变换的一种方法就是先进行部分分式展开，然后逐项求其反变换。

这种方法依赖于将 $X(z)$ 展开成如下形式的部分分式：

$$X(z)=\sum _{i=1}^m\frac{A_i}{1-a_i{z}^{-1}}\text{\hspace{1em}(11)}$$

若 $X(z)$ 的 $ROC$ 是位于极点 $z=a_i$ 的外边，那么其对应项的反变换就是 $A_i{a}_i^{n}u[n]$；另一方面，若 $X(z)$ 的 $ROC$ 是位于极点 $z=a_i$ 的里面，那么对应项的反变换就是 $-A_i{a}_i^{n}u[-n-1]$。

• 确定 $z$ 反变换的另一种方法是建立在 $X(z)$ 的幂级数展开的基础之上。由 $ X(z) =\sum_{n=-\infty}^{{+\infty}x[n]z}{-n}$ 可知，实际上 $z$ 变换就是涉及 $z$ 的正幂和负幂的一个幂级数，这个幂级数的系数就是序列值 $x[n]$。

用幂级数展开法来求 $z$ 反变换对非有理的 $z$ 变换式特别有用。

4. $z$ 变换的性质

4.1. 线性

若

$$x_1[n]\stackrel{z}{\leftrightarrow }{X}_1(z)ROC=R_1$$

和

$$x_2[n]\stackrel{z}{\leftrightarrow }{X}_2(z)ROC=R_2$$

则

$$\boxed{a{x}_1[n]+b{x}_2[n]\stackrel{z}{\leftrightarrow }a{X}_1(z)+b{X}_2(z)ROC包括R_1\cap R_2}\text{\hspace{1em}(12)}$$

4.2. 时移性质

若

$$x[n]\stackrel{z}{\leftrightarrow }X(z)ROC=R$$

则

$$\boxed{x[n-n_0]\stackrel{z}{\leftrightarrow }{z}^{-n_0}X(z)ROC=R原点或无限远点可能加上或除掉}\text{\hspace{1em}(13)}$$

4.3. $z$ 域尺度变换

若

$$x[n]\stackrel{z}{\leftrightarrow }X(z)ROC=R$$

则

$$\boxed{z_0^{n}x[n]\stackrel{z}{\leftrightarrow }X(\frac{z}{z_0})ROC=|z_0|R}\text{\hspace{1em}(14)}$$

这就是说，若 $z$ 是在 $X(z)$ 的 $ROC$ 内的一点，那么点 $|z_0|z$ 就在 $X(z/z_0)$ 的 $ROC$ 内。

4.4. 时间反转

若

$$x[n]\stackrel{z}{\leftrightarrow }X(z)ROC=R$$

则

$$\boxed{x[-n]\stackrel{z}{\leftrightarrow }X(\frac{1}{z})ROC=\frac{1}{R}}\text{\hspace{1em}(15)}$$

这就是说，若 $z_0$ 是在 $x[n]$ 的 $z$ 变换 $ROC$ 内，那么点 $1/z_0$ 就在 $x[-n]$ 的 $z$ 变换 $ROC$ 内。

4.5. 时间扩展

若令 $k$ 是一个正整数，并且定义

$$x_{(k)}[n]=\{\begin{array}{ll}x[n/k]& \text{当}n为k的整数倍\\ 0,& \text{当}n不为k的整数倍\end{array}\text{\hspace{1em}(16)}$$

若

$$x[n]\stackrel{z}{\leftrightarrow }X(z)ROC=R$$

则

$$\boxed{x_{(k)}[n]\stackrel{z}{\leftrightarrow }X(z^k)ROC=R^{1/k}}\text{\hspace{1em}(17)}$$

这就是说，若 $z$ 是在 $X(z)$ 的 $ROC$ 内，那么点 $z^{1/k}$ 就在 $X(z^k)$ 的 $ROC$ 内。

4.6. 共轭

若

$$x[n]\stackrel{z}{\leftrightarrow }X(z)ROC=R$$

则

$$\boxed{x^{\ast }[n]\stackrel{z}{\leftrightarrow }{X}^{\ast }(z^{\ast })ROC=R}\text{\hspace{1em}(18)}$$

4.7. 卷积性质

若

$$x_1[n]\stackrel{z}{\leftrightarrow }{X}_1(z)ROC=R_1$$

和

$$x_2[n]\stackrel{z}{\leftrightarrow }{X}_2(z)ROC=R_2$$

则

$$\boxed{x_1[n]\ast x_2[n]\stackrel{z}{\leftrightarrow }{X}_1(z)X_2(z)ROC包括R_1\cap R_2}\text{\hspace{1em}(19)}$$

4.8. $z$ 域微分

若

$$x[n]\stackrel{z}{\leftrightarrow }X(z)ROC=R$$

则

$$\boxed{nx[n]\stackrel{z}{\leftrightarrow }-z\frac{dX(z)}{dz}ROC=R}\text{\hspace{1em}(20)}$$

4.9. 初值定理

若 $n<0,x[n]=0$，则

$$x[0]=\underset{z\to \infty }{\lim }X(z)\text{\hspace{1em}(21)}$$

4.10. 终值定理

若 $n<0,x[n]=0$，其 $z$ 变换的极点，除可以有一个一阶极点在 $z=1$ 上，其它极点均在单位圆内，则

$$\underset{n\to \infty }{\lim }x[n]=\underset{z\to 1}{\lim }(z-1)X(z)\text{\hspace{1em}(21)}$$

4.11. 性质小结

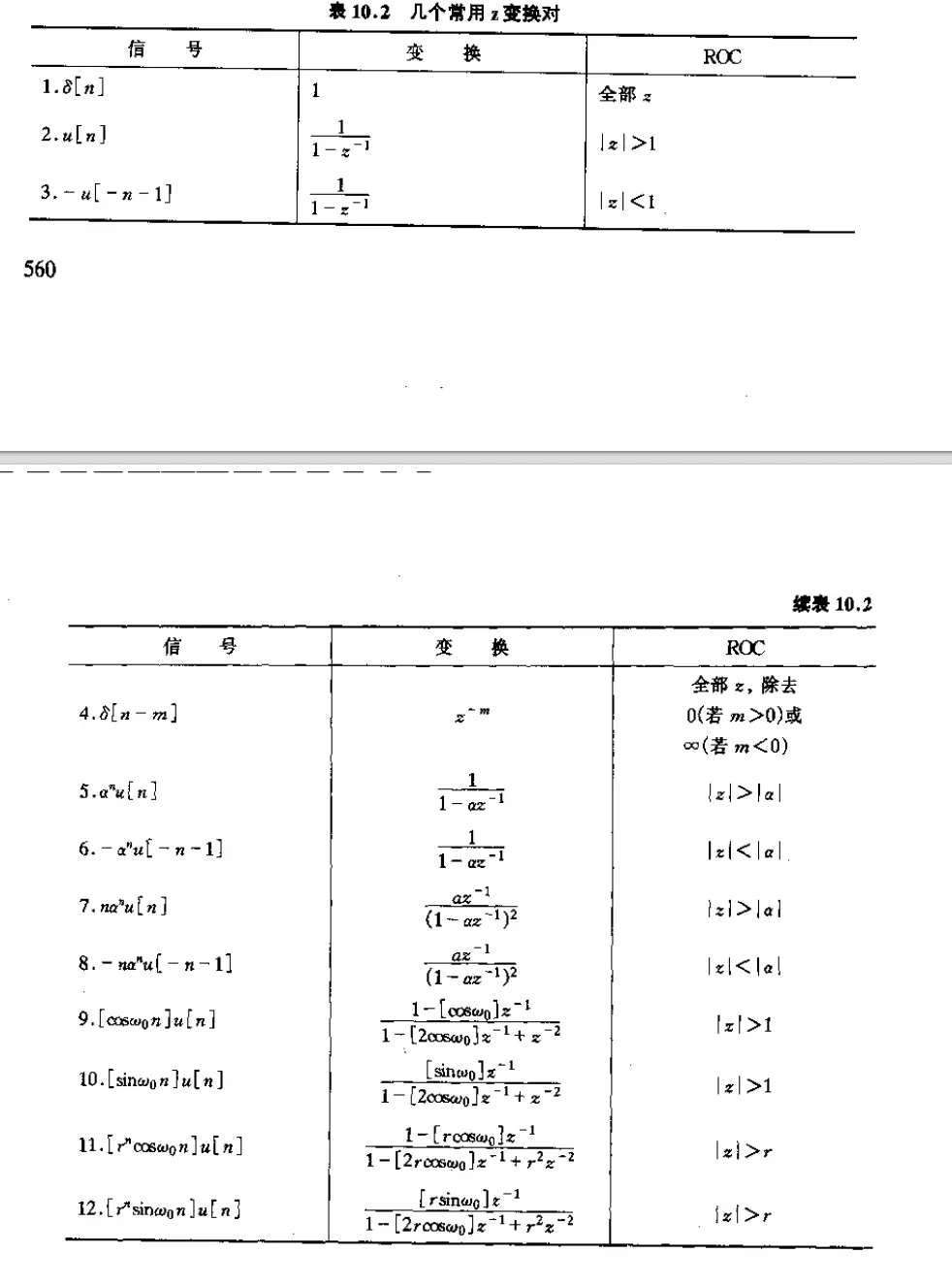
4.12. 几个常用的 $z$ 变换对

5. 利用 $z$ 变换分析与表征线性时不变系统

在离散时间 $LTI$ 系统的分析和表示中，$z$ 变换有其特别重要的作用，由卷积性质可得

$$Y(z)=H(z)X(z)\text{\hspace{1em}(23)}$$

式中 $X(z)、Y(z)、H(z)$ 分别是系统输入、输出和单位脉冲响应的$z$ 变换 。$H(z)$ 称为系统的系统函数或转移函数。

5.1. 因果性

一个因果 $LTI$ 系统其单位脉冲响应 $h[n]$是对于 $n<0，h[n]=0$，因此是一个右边序列。由性质 4 知道 $H(z)$ 的 $ROC$ 是位于 $z$ 平面内某一个圆的外边。由性质 8 可知，对于一个因果序列，这个幂级数中，

$$H(z)=\sum _{n=0}^{\infty }h[n]z^{-n}\text{\hspace{1em}(24)}$$

不包含任何 $z$ 的正幂次项，因此 $ROC$ 包括无限远点。综上所述，就得出如下属性：

一个离散时间 $LTI$ 系统当且仅当它的系统函数的 $ROC$ 是在某一个圆的外边，且包括无限远点，该系统就是因果的。

如果 $H(z)$ 是有理的，那么该系统要是因果的，其 $ROC$ 必须位于最外层极点的外边，且无限远点必须在 $ROC$ 内；等效地说，随 $z\to \infty$ 时， $H(z)$ 的极限必须是有限的。这就等效于，当 $H(z)$ 的分子和分母都是表示成的 $z$ 的多项式时，其分子的阶次不会大于分母的阶次。即

一个具有有理系统函数 $H(z)$ 的 $LTI$ 系统要是因果的，当且仅当：(1) $ROC$ 位于最外层极点某一个圆的外面；和 (2) 若 $H(z)$ 表示成 $z$ 的多项式之比，其分子的阶次不能大于分母的阶次。

5.2. 稳定性

一个离散时间 $LTI$ 系统的稳定性就等效于它的单位脉冲响应是绝对可和的，在这种情况下， $h[n]$ 的傅里叶变换收敛，结果就是 $H(z)$ 的 $ROC$ 必须包括单位圆。综上所述，可得如下结果：

一个 $LTI$ 系统当且仅当它的系统函数 $H(z)$ 的 $ROC$ 包括单位圆，该系统就是稳定的。

对于一个具有有理系统函数的因果系统而言，$ROC$ 位于最外层极点的外边。对于这个包括单位圆的 $ROC$ ，系统的全部极点都必须位于单位圆内，即

一个具有有理系统函数的因果 $LTI$ 系统，当且仅当 $H(z)$ 的全部极点都位于单位圆内时，也即全部极点模均小于 1 时，系统就是稳定的。

5.3. 由线性常系数差分方程表征的 $LTI$ 系统

对于一般的 $N$ 阶差分方程，可以对方程两边进行 $z$ 变换，并利用线性和时移性质。现考虑一个 $LTI$ 系统，其输入、输出满足如下线性常系数差分方程：

$$\sum _{k=0}^N{a}_{k}y[n-k]=\sum _{k=0}^M{b}_{k}x[n-k]\text{\hspace{1em}(25)}$$

对式（25）两边取 $z$ 变换，可得

$$\sum _{k=0}^N{a}_k{z}^{-k}Y(z)=\sum _{k=0}^M{b}_k{z}^{-k}X(z)\text{\hspace{1em}(26)}$$

这样就有

$$H(z)=\frac{Y(z)}{X(z)}=\frac{\sum _{k=0}^M{b}_k{z}^{-k}}{\sum _{k=0}^N{a}_k{z}^{-k}}\text{\hspace{1em}(27)}$$

获取更多精彩，请关注「seniusen」!