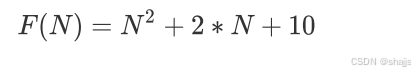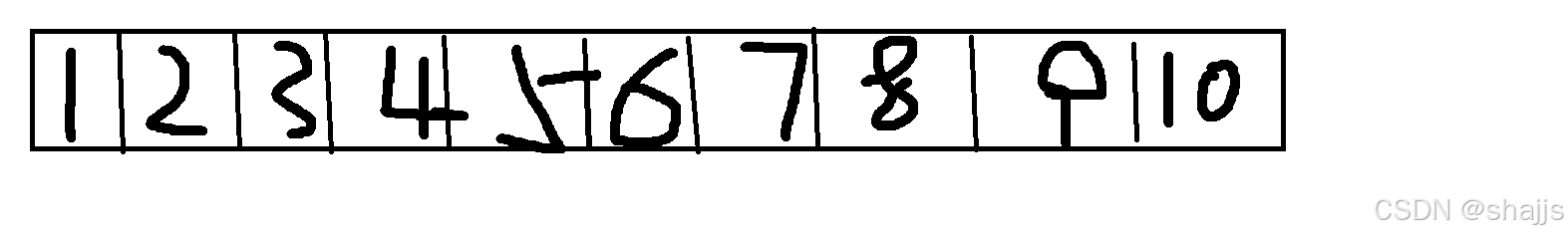一.什么是集合框架
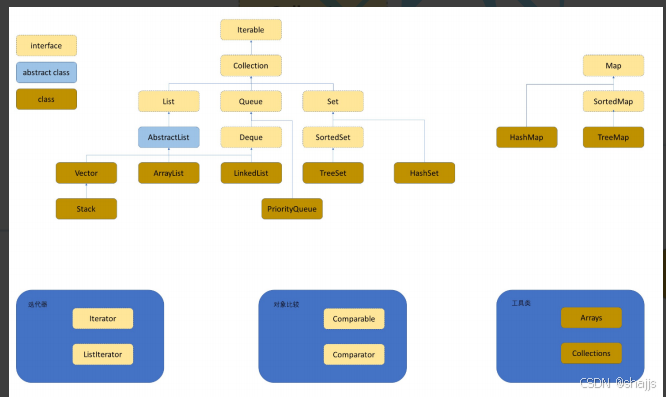
二. 集合框架的重要性
使用成熟的集合框架,有助于我们便捷、快速的写出高效、稳定的代码。
学习背后的数据结构知识,有助于我们理解各个集合的优缺点及使用场景。
三.背后所涉及的数据结构以及算法
3.1 什么是数据结构
3.2 容器背后对应的数据结构
3.3 什么是算法
四.时间和空间复杂度
4.1 算法效率
4.2 时间复杂度
4.2.1 概念
4.2.2 大O的渐进表示法
Func1 执行的基本操作次数 :
4.2.3 计算原则
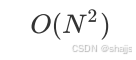
4.2.4 算法例子
例一
先求执行次数的和,就是2N+10,根据上面的规则,最终答案就是O(N)。
例二:
计算次数就是M+N,根据计算规则结果就是O(M+N)。
例三
执行了一百次,常数都看作是1,所以是O(1)。
例四
要结合着算法思想,如图算法,可设array.length=n,第一次执行了n-1次,第二次执行了n-2次,.........,所以总和就是n-1+n-2+n-3+.......+2,等差数列求和公式算出总和,再根据算法规则,可得结果是O(N的平方)。
例五
array数列必须是有序的,可以升序也可以降序。
在上述二分查找的代码中,每次循环都会将搜索范围缩小一半
假设数组的长度为 n。
在第一次循环时,搜索范围是 n 个元素。
第二次循环时,搜索范围缩小为 n/2 个元素。
第三次循环时,搜索范围缩小为 n/4 个元素。
以此类推,直到找到目标元素或者确定目标元素不存在。
假设循环了 k 次找到了目标元素或者确定目标元素不存在,那么有 n / 2^k = 1,即 2^k = n,所以 k = log₂(n)。
因此,二分查找的时间复杂度为 O(log₂(n)) 。这意味着随着数组长度的增加,二分查找的运行时间增长速度相对较慢,具有较好的性能。
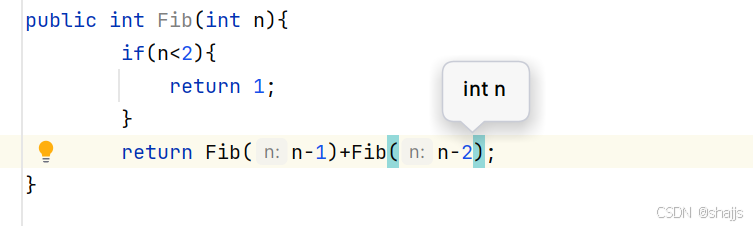
例六
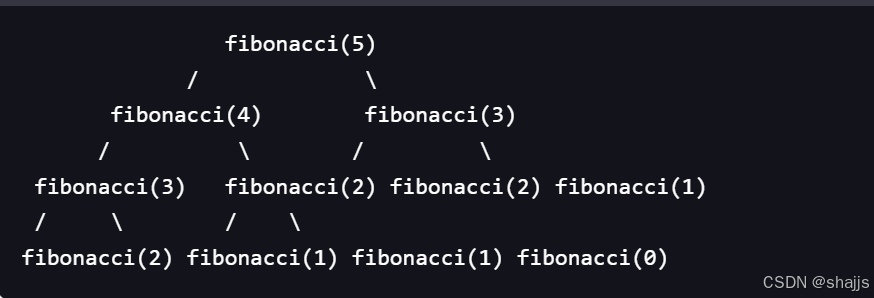
递归公式
递归的时间复杂度=递归的次数 * 每次递归执行的次数
上面都是符合2的n次方的规律的,只有最后一行不符合,但是这个计算本来也是粗略的,所以可以把最后一行也看作符合规律,不影响结果,所以就是2的0次方+2的1次方,一直加到2的n-1次方,等比数列求和得到是2的n次方-1,根据算法规则,等到O(2的n次方)。
4.3 空间复杂度
4.3.1 概念
4.3.2 例子
例一
上述冒泡排序的代码在执行过程中没有额外开辟新的数组或其他数据结构来存储数据,它只是在原数组上通过交换元素的位置来进行排序操作。
因此,它开辟的额外空间为 O(1),即常量级别的空间。
例二
如图,通过new关键字开辟了n+1个空间所以空间复杂度是O(n)。
例三
实例3递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)。
五.包装类
5.1 概念
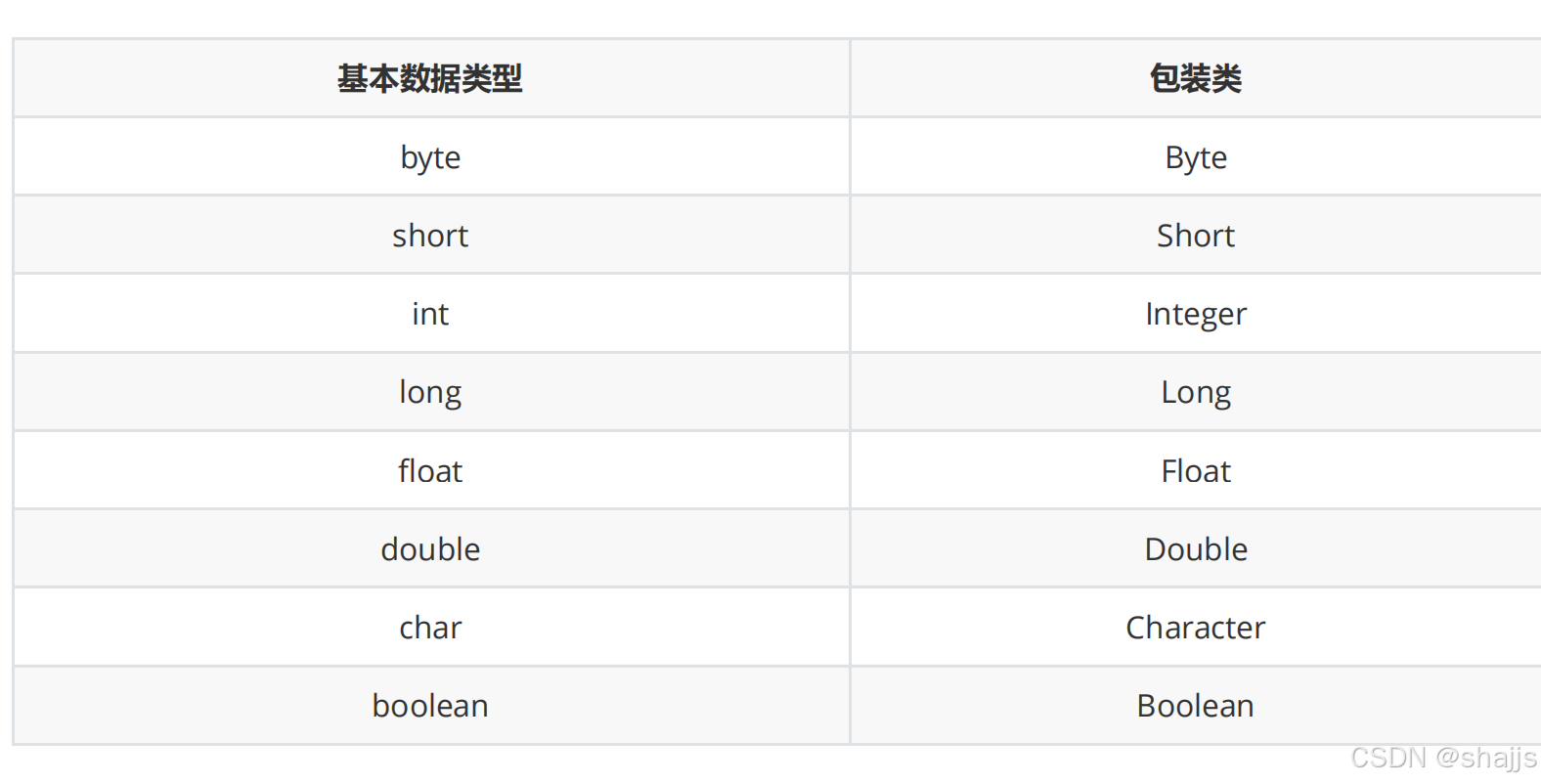
5.2 基本数据类型和对应的包装类
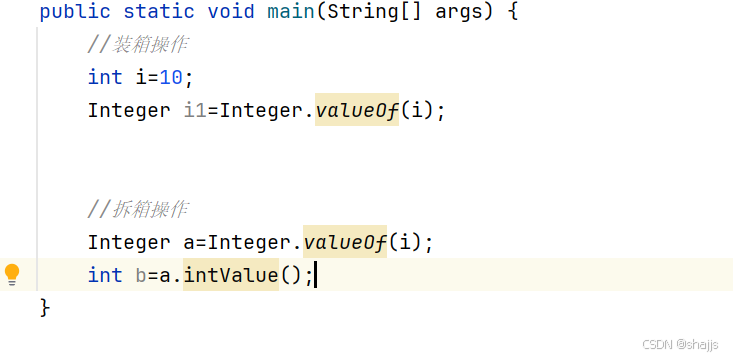
5.3 拆箱和装箱操作
装箱就是把数据放到包装类中,拆箱就是从包装类中拿出来。
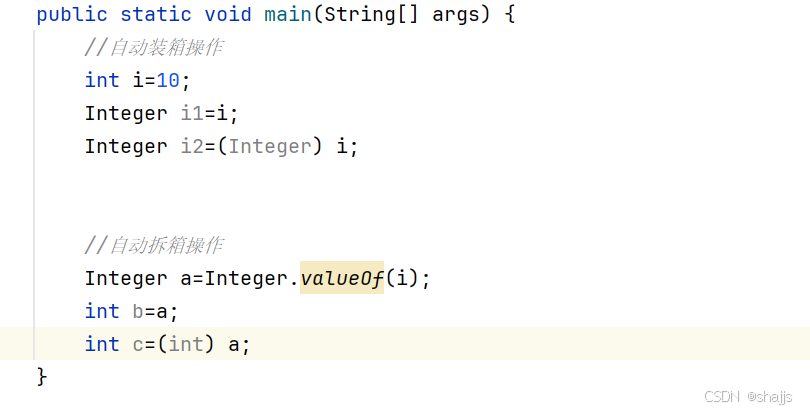
5.4 自动装箱和拆箱
直接让它等于,Java会帮我们进行装箱和拆箱的操作。
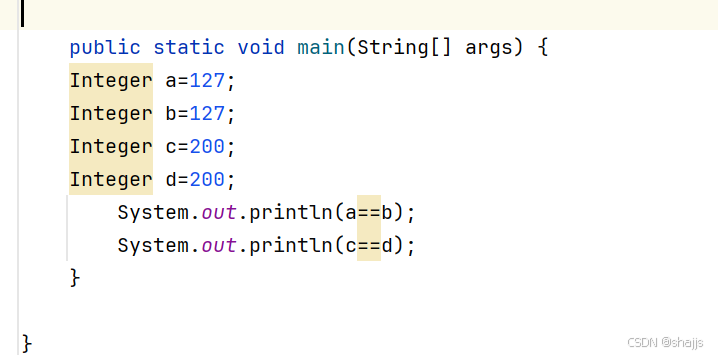
思考一下会输出什么?
原因就是
这是因为在 Java 中,对于值在 -128 到 127 之间的 Integer 对象,通过自动装箱操作(如 Integer a = 127; )得到的对象会被缓存起来,当再次创建相同值的 Integer 对象时,会直接返回缓存中的对象,所以 a 和 b 指向同一个对象,a == b 为 true 。
而对于值不在 -128 到 127 之间的 Integer 对象,每次装箱都会创建新的对象,所以 c 和 d 是两个不同的对象,c == d 为 false 。
5.5 转换类型
可以把int类型的a包装后,转换为double类型。
六 初识泛型
6.1 什么是泛型
泛型是 Java 等编程语言中的一个特性,它允许在定义类、接口和方法时使用类型参数,使得这些代码可以在多种数据类型上进行操作,同时在编译时进行类型检查,以增强代码的类型安全性和可读性。
通过使用泛型,可以编写更通用、灵活且类型安全的代码。例如,在定义一个集合类(如 ArrayList )时,可以使用泛型来指定集合中元素的类型,这样在编译阶段就可以检查添加到集合中的元素类型是否正确,避免了运行时的类型转换错误。
简单来说,泛型让代码能够处理不同类型的数据,同时保证类型的正确性,提高了代码的复用性和可维护性。
6.2 引出泛型
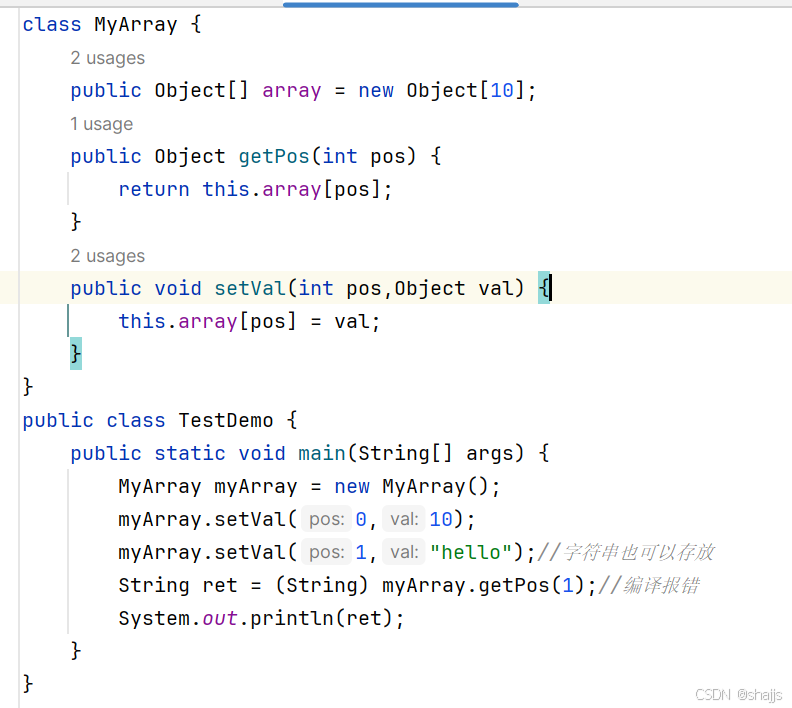
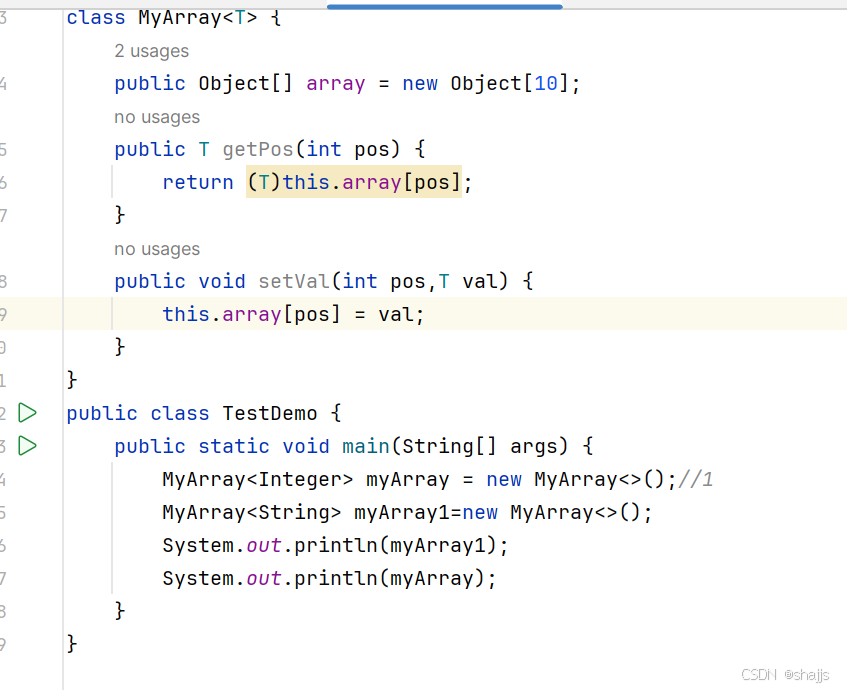
我们要完成实现一个类,类中包含一个数组成员,使得数组中可以存放任何类型的数据,也可以根据成员方法返回数组中某个 下标的值。
我们要怎么实现呢?
这样可以,但是太乱了,还需要强制类型转换,否则会报错。
我们之前学的int String数组都只能存放一些特定类型的值,无法存放任意类型的值,那么我们要怎么实现呢?接下来我们就得用到泛型这个概念了。
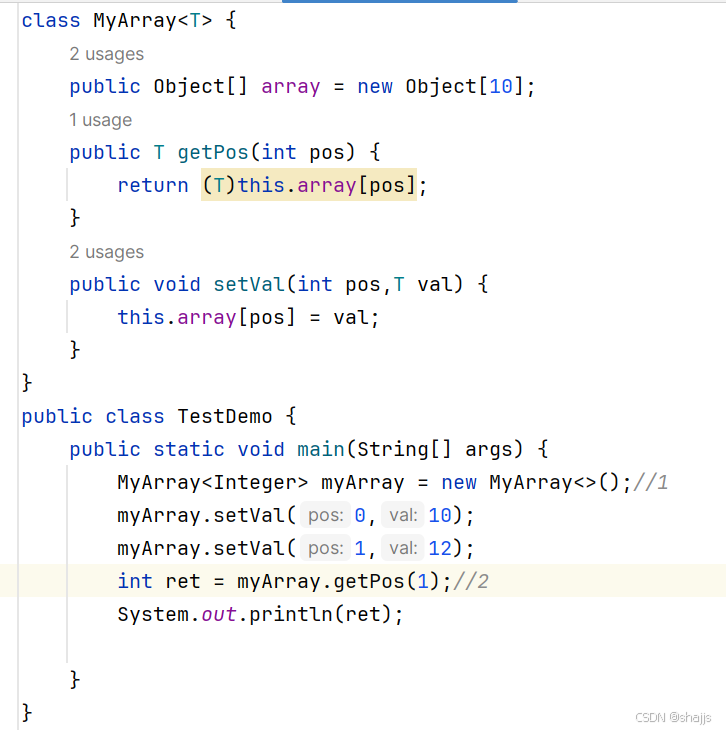
6.3 泛型的语法
T是标识符的一种。
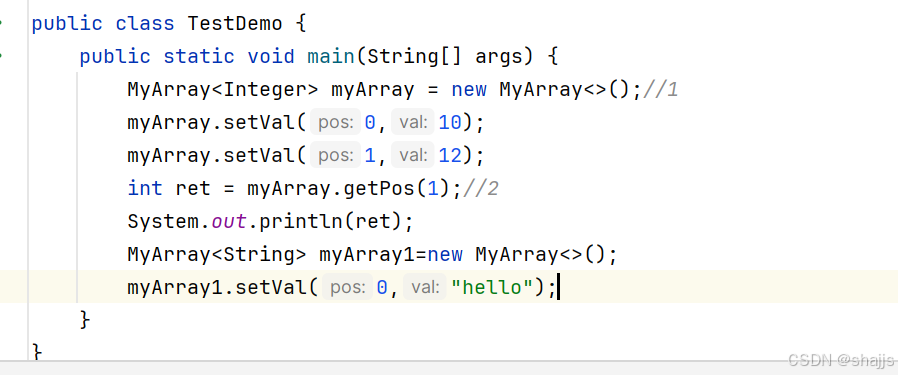
Integer限制只能填正数,如果想填字符串,可以再建一个,换一下标识符内容即可。
如下图所示
6.3.1 标识符
6.4:泛型的擦除机制
6.4.1 概念
在 Java 中,泛型的擦除机制是指在编译过程中,将所有的泛型参数替换为特定的类型,这个类型通常是Object,或者如果有限定类型,则使用该限定类型。
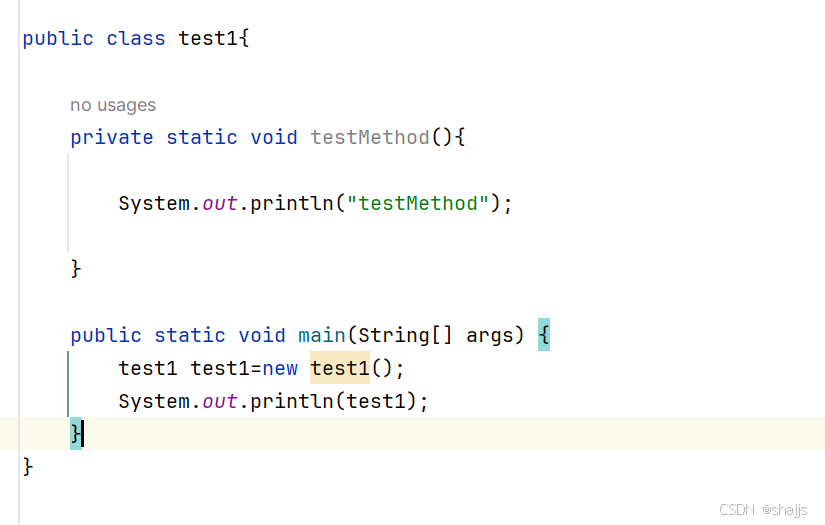
6.4.2 例子
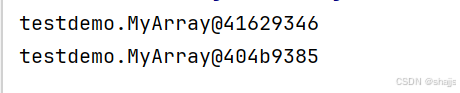
输出了类型加地址。
我们希望我们的泛型也是这样。如下图:
testdemo是我们的包,不用管,而后面它把Integer和String擦除了,在使用的时候也会把T擦除为Object。
6.5:泛型的上界
加个上界Number。
发现报错了,加了extends Number之后表示,只能写Number类或者是Number的子类,可知Integer是Number的子类,而String不是。
6.6:泛型实现接口
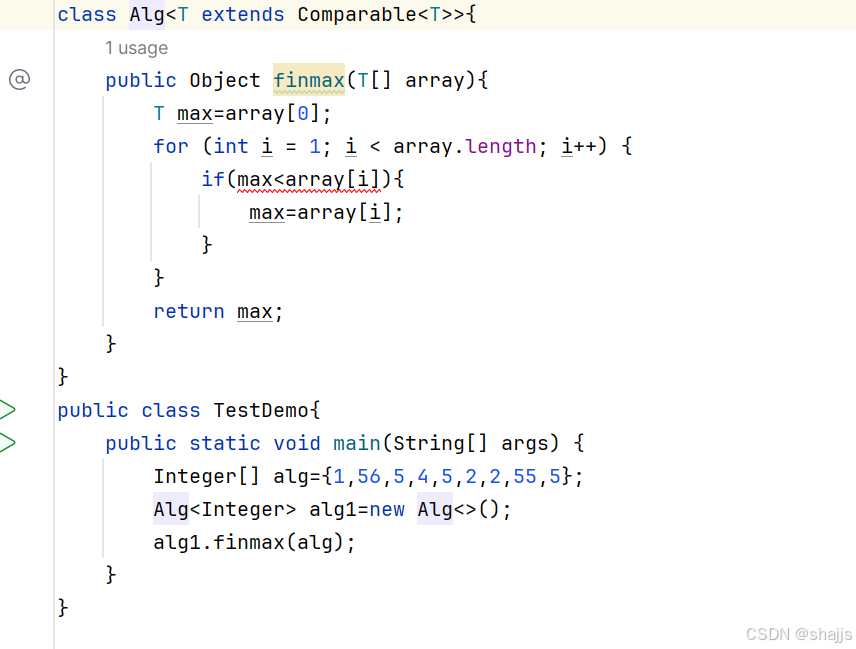
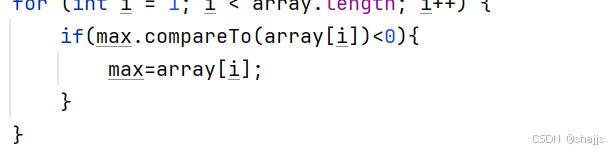
我们先实现一个功能,定义一个泛型找最大值。
为什么会报错呢?
对于泛型类型 T ,不能直接使用小于号 < 进行比较。因为在编译阶段,泛型的具体类型是不确定的,编译器无法确定 T 类型是否支持 > 、 < 这样的操作。
怎么改呢?
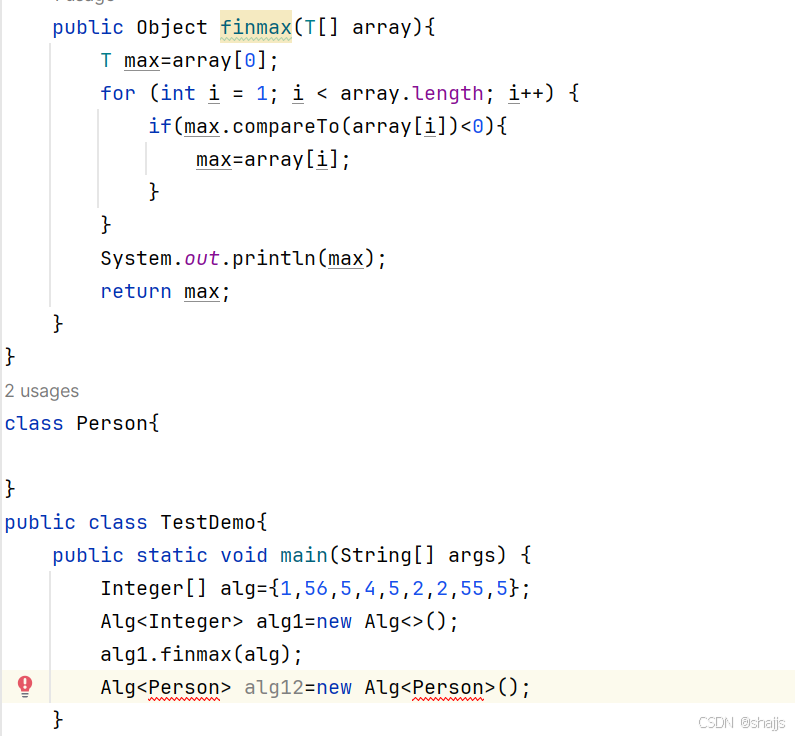
现在实现了Comparable接口,所以可以使用CompareTo方法来比较。
如图进行了修改。
此时就可以了。
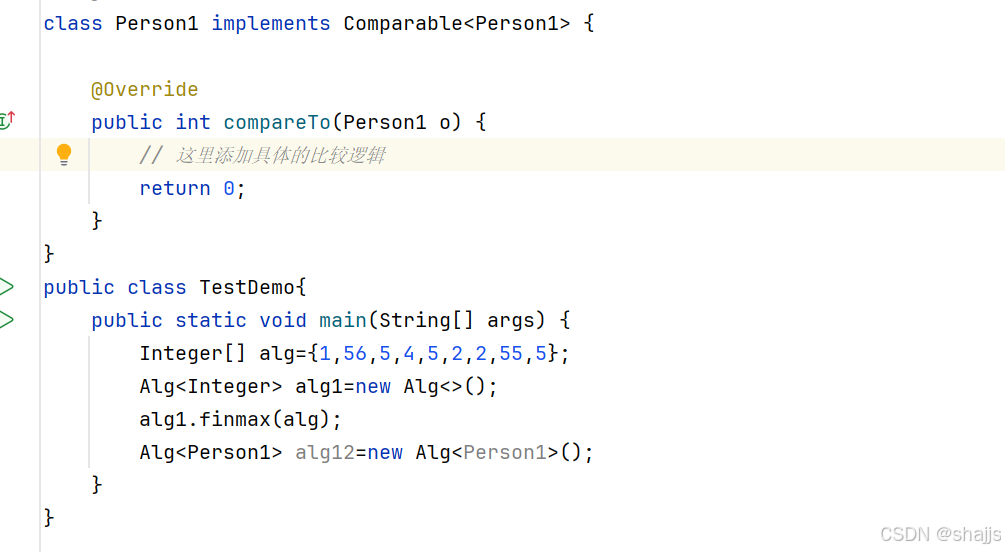
为什么报错,因为Person没有实现Comparable接口。
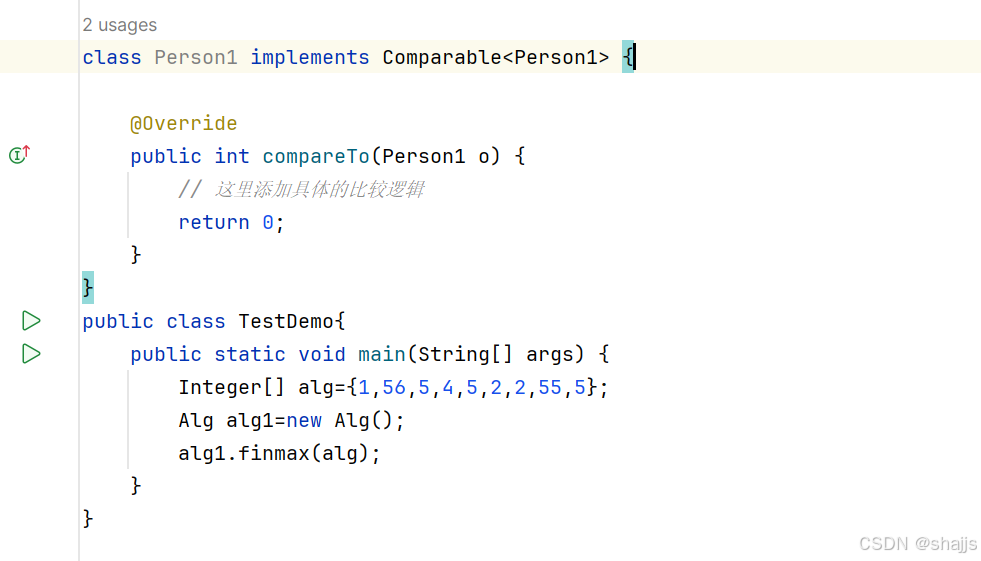
这样就可以了。
6.7 泛型方法
如图所示,将泛型写到方法里面,也是可以的。
不想实例化对象调用finmax方法的话,需要在public后面加一个static即可。
七.结束语
感谢大家的查看,希望可以帮助到大家,做的不是太好还请见谅,其中有什么不懂的可以留言询问,我都会一一回答。 感谢大家的一键三连。