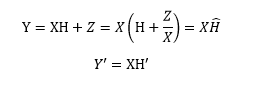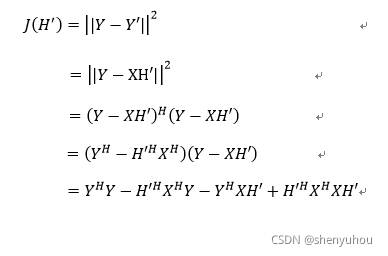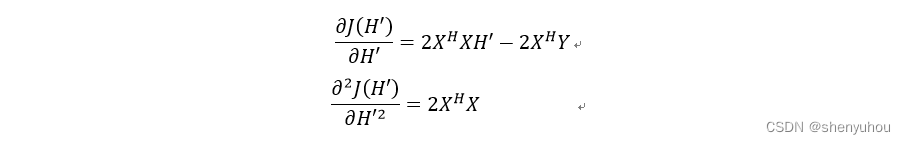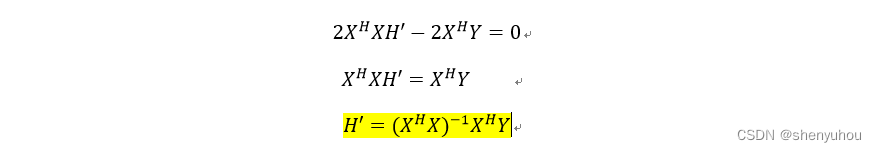前言
信道估计是通信系统接收机的重要功能模块,主要是用来估计信号所经历信道的冲击响应,并用于后续的信道均衡处理,以便消除多径信号混叠造成的ISI。
信道估计的方法有很多种,大体上可分为两类,一类是基于训练序列的信道估计,而另一类是信道的盲估计(自适应估计),其估计过程不依赖已知信息。常见通信系统的信道估计,绝大部分是基于训练序列的估计方法,这里面最最常用的两个信道估计算法就是LS算法和MMSE算法。LS是最小二乘、MMSE是最小均方误差,它们都是所谓的最优化准则,即得到最优信道估计所遵循的准则,有时也被称为代价函数。
LS信道估计的原理
建立如下信号关系式:
其中Y为实际接收数据,Y’为估计的接收数据,其大小均为N1X1的矩阵(N1为参与LSCE计算的数据数量),Z 为噪声也是一个N1X1的矩阵,H是真实信道矩阵,H’是估计信道矩阵,大小为N2X1(N2为估计的多径数量)。X为发送数据矩阵,是一个N1XN2的矩阵,其包含的数据为按行进行符号延迟的数据。
首先明确一点,在LS估计中,我们使用Y和Y‘’来进行计算,估计出的结果是H’而并非H,若估计的结果H’使得Y’与Y误差最小,则能得到的结果应该是H’与H(带三角)的误差最小,但H(带三角)也不是真实的信道矩阵,其内还包含了一个误差项Z/X,因此对于LS信道估计而言,其结果的精度是受这个误差项影响的,而这个误差项概括来说就是和SNR相关,SNR越大,误差项越小,LS估计精度越高。
现依据LS最优准则对上式中H’进行估计,首先给出LS准则的代价函数
能使代价函数J(H’)取到最小值的H’则是我们求的最优信道矩阵,下面通过分析代价函数对H’的一阶导数和二阶导数,来确定J(H’)的最小值位置。
因为XHX为正定矩阵,所以J(H’)为自变量H’的凹函数,则其一阶导数的零点即对应了该函数的极小值位置。依据这个理论能直接计算出代价函数J(H’)极小值时的H’,这也就是对信道矩阵的LS最佳估计。
上式中的H’就是LS信道估计的结果,可见其计算过程需要对X的自相关矩阵进行求逆运算,在实际使用中,因为X矩阵是已知的,因此XHX的逆矩阵可以提前计算出来,而不用在代码实现中再进行求逆运算,从而简化计算过程。
总结
通过上面的分析可知,LS信道估计使用的优化准则为:实际接收数据(实际观测量)与估计的接收数据(估计观测量)之间的误差平方和最小。这就造成了估计出来的信道矩阵与实际的信道矩阵存在一定误差,而且这个误差会随着信噪比的降低越来越大,这也是为什么LS信道估计不适合应用在信噪比较低的场景中。那如果实际使用的场景存在低SNR的情况怎么办呢,这就引出了另外一种信道估计算法–MMSE估计。