文章目录
本文为吴恩达机器学习课程的笔记系列第六篇,主要关于数据降维时常用的算法-PCA主成分分析算法,同时扩展另一算法-ICA 独立成分分析。
主成分分析 PCA
学习主成分分析之前,我们首先来了解什么是降维。
什么是降维
参考西瓜书的定义,降维即通过某种数学变换将原始高维属性空间转变为一个低维子空间。在这个子空间中样本密度大幅提高,距离计算也会变得更容易。
其实降维一般就是从高维投影到低维。
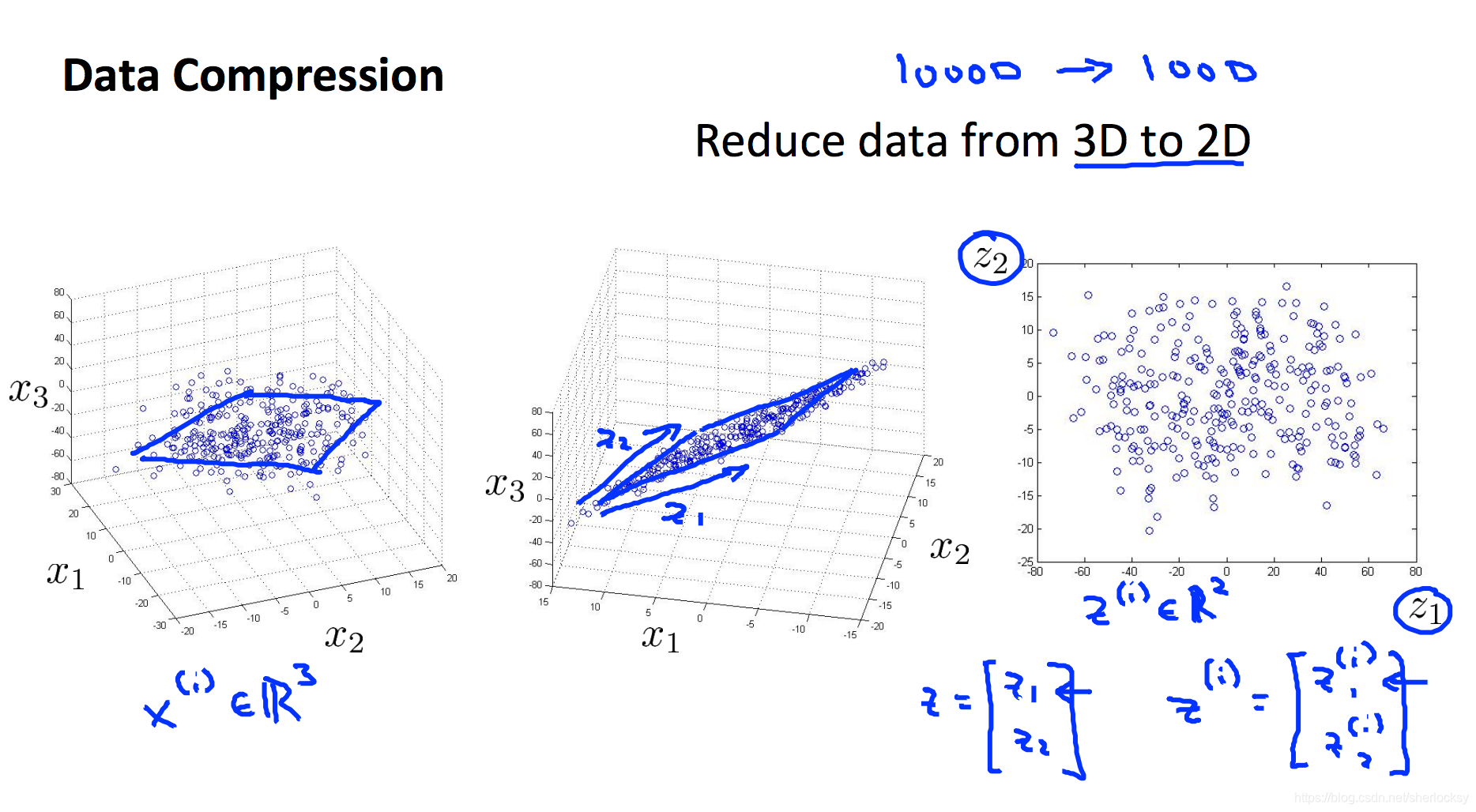
例如下图,对于3维数据,降到2维即是把数据从原来的3维空间投影到2维平面,这就实现了降维。
PCA (Principal Component Analysis)
主成分分析是最常见的降维算法。PCA 能从冗余特征中提取主要成分,在不太损失模型质量的情况下,提升了模型训练速度。
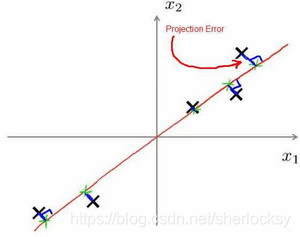
投影误差(Projection Error):
投影误差就是:把数据投影到一个经过原点的向量(即方向向量),此时的特征向量与该方向向量垂线的长度。
PCA的目标是,我们希望找到一个方向向量(Vector direction),使得这个投影误差的均方误差尽可能地小。
显然这是个降到一维的例子。那PCA的完整描述是:
想要将n维数据降至k维,那目标就是要找到这样的一组向量 u 1 , u 2 , u 3 , . . . , u k u_1,u_2,u_3,...,u_k u1,u2,u3,...,uk ,使得所有数据投影在这组向量上的总的投影误差最小。实际上这组向量在原始空间上应该是正交的。而这k维全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
算法流程
-
均值归一化。
-
计算协方差矩阵:
Σ = 1 m ∑ i = 1 n ( x ( i ) ) ( x ( i ) ) T = 1 m X T X \Sigma = \dfrac{1}{m} \sum\limits_{i=1}^{n}(x^{(i)})(x^{(i)})^T = \dfrac{1}{m} X^TX Σ=m1i=1∑n(x(i))(x(i))T=m1XTX
-
通过奇异值分解计算协方差矩阵 Σ \Sigma Σ 的特征向量:
( U , S , V T ) = S V D ( Σ ) (U,S,V^T)=SVD(\Sigma) (U,S,VT)=SVD(Σ)
-
从 U U U 中选取前 k k k 个向量,获得一个 n × k n\times k n×k 维度的矩阵,用 U r e d u c e U_{reduce} Ureduce 表示。 k k k 的意思是我们希望将数据从 n n n 维降至 k k k 维。
-
计算新的特征向量 z ( i ) z^{(i)} z(i):
z ( i ) = U r e d u c e T ∗ x ( i ) z^{(i)}=U^T_{reduce} * x^{(i)} z(i)=UreduceT∗x(i)
显然,最终的结果自然是 k × 1 k \times 1 k×1 维度。
总的来说,想要得到主成分,先计算数据矩阵的协方差矩阵,再通过奇异值分解得到协方差矩阵的特征向量,然后选择特征值最大的也就是方差最大的k个特征向量组成的矩阵。
小结一下,PCA作为一个非监督学习的降维方法,它只需要特征值分解,就可以对数据进行压缩,去噪。因此在实际场景应用很广泛。
独立成分分析 ICA
上面的PCA是一个信息提取的过程,用于对原始数据进行降维,而接下来所提到的独立成分分析 即ICA(Independent Component Analysis),是一个信息解混的过程。
问题引入
ICA的前提是认为观察变量是若干个统计独立的分量的线性组合。
我们先从经典的鸡尾酒宴会问题(ocktail party problem)来讨论。这个问题是这样的:在一个房间里有 n n n 个人在开 party,他们可以同时说话。房间的不同角落里放置了 n n n 个声音接收器,每个接收器可以在每个时刻同时采集到 n n n 个人声音的重叠声音。每个接收器和每个人的距离是不一样的,所以每个接收器接收到的声音的重叠情况也不同。party结束后,我们得到 m m m 个声音样本,每个样本是在具体时刻 i i i,从 n n n 个接收器接采集的一组声音数据,如何从这 m m m 个样本集分离出 n n n 个说话者各自的声音呢?
我们仔细来看这个问题描述,用 s s s 来表示每个人在所有时刻所发出的声音信号源,它是一个 n × m n\times m n×m 的矩阵,每一行表示一个人