目录
实验内容:
1. 编写函数,采用邻接矩阵表示法,构造一个无向网。
2. 编写函数,实现从键盘输入数据,建立一个有向图的邻接表。
3. 编写函数,输出该邻接表。
4. 编写函数,采用邻接表存储实现无向图的深度优先非递归遍历。
5. 编写函数,采用邻接表存储实现无向图的广度优先遍历。
6. 编写一个主函数,在主函数中设计一个简单的菜单,分别调试上述算法。
源码:
#include <iostream>
#include <string>
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <iomanip>
using namespace std;
#define MAX_VERTEX_NUM 10 // 顶点最大个数
//#define INF 65535
// 邻接矩阵
// 无向网
struct UnGraph {
int Vertex[MAX_VERTEX_NUM]; // 顶点集
int arc[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 无向网的邻接矩阵(元素为权值)
int vexNum; // 顶点个数
int eNum; // 边的条数
};
// 创建无向网
void creatUnGraph(UnGraph& unG) {
int vexCount; // 顶点数
int i, j, w; // 点、边下标、权
while (true) {
cout << "请输入顶点个数: " << endl;
cin >> vexCount;
if (vexCount < 10 && vexCount > 0) {
unG.vexNum = vexCount;
break;
}
else {
cout << "您输入的顶点个数有误,请重新输入" << endl;
}
}
cout << "请输入边的条数: " << endl;
cin >> unG.eNum;
cout << "请输入顶点信息, 如0 1 2 3 4 " << endl;
for (int i = 0; i < unG.vexNum; i++) {
cin >> unG.Vertex[i];
}
// 邻接矩阵初始化
for (int i = 0; i < unG.vexNum; i++) {
for (int j = 0; j < unG.vexNum; j++) {
unG.arc[i][j] = 0;
}
}
// 输入邻接矩阵信息
for (int k = 0; k < unG.eNum; k++) {
cout << "请输入边(Vi,Vj)的下标i, j以及权值w" << endl;
cin >> i >> j >> w;
unG.arc[i][j] = w;
// 无向网的邻接矩阵对称
unG.arc[j][i] = unG.arc[i][j];
}
}
// 输出无向网的邻接矩阵
void printUnG(UnGraph& unG) {
cout << endl;
for (int i = 0; i < unG.vexNum; i++) {
for (int j = 0; j < unG.vexNum; j++) {
printf("%8d", unG.arc[i][j]);
}
cout << endl;
}
}
// 邻接表
typedef char VerTexData; // 顶点数据类型
// 边节点
typedef struct arcNode
{
int ajdVex;// 目标节点位置
struct arcNode* nextArc; // 下一边链接指针
}arcNode;
// 顶点结点
typedef struct VerTexNode
{
VerTexData data; // 顶点值
arcNode* adjArc; // 顶点的第一条边
}VerTexNode;
// 有向图
typedef struct AdjGraph
{
VerTexNode VexList[MAX_VERTEX_NUM]; // 邻接表
int vexNum; // 有向图的顶点个数
int eNum; // 无有图的边数
}AdjGraph;
// 创建有向图的邻接表
void CreatGraph(AdjGraph& G)
{
int head; // 边头
int tail; // 边尾
cout << "请输入图的顶点数和边数" << endl;
cin >> G.vexNum >> G.eNum;
cout << "请输入顶点信息,如 0 1 2 3:\n";
for (int i = 0; i < G.vexNum; i++) // 输入顶点信息
{
cin >> G.VexList[i].data;
G.VexList[i].adjArc = NULL; // 初始化顶点的第一条边
}
cout << "逐条边输入,分别输入头,尾:\n";
for (int i = 0; i < G.eNum; i++)
{
cin >> head >> tail; // 逐边输入
arcNode* p = new arcNode;
p->ajdVex = tail;
p->nextArc = G.VexList[head].adjArc;
G.VexList[head].adjArc = p;
}
}
// 输出有向图的邻接表
void ShowGraph(AdjGraph G)
{
for (int i = 0;i < G.vexNum;i++)
{
cout << G.VexList[i].data;
arcNode* p = G.VexList[i].adjArc;
while (p != NULL)
{
cout << " -> " << p->ajdVex;
p = p->nextArc;
}
cout << "\n";
}
}
//无向图
typedef struct ALGraph {
VerTexNode AdjList[MAX_VERTEX_NUM]; // 邻接表
int vexnum, arcnum; // 图的顶点数和边数
}ALGraph;
// 在图G中查找顶点v,存在则返回顶点表中的下标;否则返回-1
int LocateVex(ALGraph G, char v) {
for (int i = 0; i < G.vexnum; i++)
if (G.AdjList[i].data == v)
return i;
return -1;
}
// 建立无向图的邻接表
void CreateAG(ALGraph& G) {
char v1, v2; // 接收输入顶点,在LocateVex中转为位次
arcNode* pi, * pj; // pi指结点i指向的结点,pj指结点j指向的结点
cout << "请依次输入图G的顶点数、边数:" << endl;
cin >> G.vexnum >> G.arcnum;
cout << "请输入各顶点信息,如 0 1 2 3:" << endl;
for (int i = 0; i < G.vexnum; i++) { // 建立顶点表,依次输入顶点值
cin >> G.AdjList[i].data; // 输入顶点值
G.AdjList[i].adjArc = NULL; // 初始化链表头指针为空
}
cout << "逐条边输入,分别输入头,尾:" << endl;
for (int k = 0; k < G.arcnum; k++) {
cin >> v1 >> v2;
int i = LocateVex(G, v1);
int j = LocateVex(G, v2);
// 以下插入方式类似于单链表头插法
pi = new arcNode;
pi->ajdVex = j; // 结点i指向的点是结点j
pi->nextArc = G.AdjList[i].adjArc; // 结点i指向的点的next点仍是结点i指向的点
G.AdjList[i].adjArc = pi; // 更新G.vertices[i]首指针
// 无向图a指向b的同时b也指向a
pj = new arcNode; pj->ajdVex = i; // 结点j指向的点是结点i
pj->nextArc = G.AdjList[j].adjArc;
G.AdjList[j].adjArc = pj; // 更新G.vertices[j]首指针
}
}
// 输出无向图的邻接表
void PrintALGraph(ALGraph G) {
for (int i = 0; i < G.vexnum; i++) {
cout << G.AdjList[i].data;
arcNode* p = G.AdjList[i].adjArc;
while (p) {
cout << "->" << p->ajdVex;
p = p->nextArc;
}
cout << endl;
}
}
//队列------------------------------------
typedef int QElemType;
const int QUEUE_INIT_SIZE = 100;
const int QUEUEINCREMENT = 10;
typedef struct {
QElemType* data;
int front;
int rear;
int queuesize;
int incresize;
}SqQueue;
bool InitQueue(SqQueue& Q, int = QUEUE_INIT_SIZE, int = QUEUEINCREMENT); // 初始化循环队列
int QueueLength(SqQueue Q); // 返回队列长度
bool DeQueue(SqQueue& Q, QElemType& e); // 将队首元素出队,用e返回
bool EnQueue(SqQueue& Q, QElemType e); // 将元素e放入循环队列
bool GetHead(SqQueue Q, QElemType& e); // 取队首元素,用e返回
bool incrementQueuesize(SqQueue& Q); // 当循环队列空间不足时,动态扩充空间
bool QueueEmpty(SqQueue Q); // 判断队列是否为空
bool InitQueue(SqQueue& Q, int maxsize, int incresize) {
Q.data = new QElemType[maxsize];
if (!Q.data)return 0;
Q.front = Q.rear = 0;
Q.queuesize = maxsize;
Q.incresize = incresize;
return 1;
}
int QueueLength(SqQueue Q) {
return (Q.rear - Q.front + Q.queuesize) % Q.queuesize;
}
bool DeQueue(SqQueue& Q, QElemType& e) {
if (Q.front == Q.rear)
return 0;
e = Q.data[Q.front];
Q.front = (Q.front + 1) % Q.queuesize;
return 1;
}
bool EnQueue(SqQueue& Q, QElemType e) {
if ((Q.rear + 1) % Q.queuesize == Q.front)
if (!incrementQueuesize(Q))
return 0;
Q.data[Q.rear] = e;
Q.rear = (Q.rear + 1) % Q.queuesize;
return 1;
}
bool GetHead(SqQueue Q, QElemType& e) {
if (Q.rear == Q.front)
return 0;
e = Q.data[Q.front];
return 1;
}
bool incrementQueuesize(SqQueue& Q) {
QElemType* newdata = new QElemType[Q.queuesize + Q.incresize];
if (!newdata)return 0;
for (int i = 0; i < Q.queuesize; i++)
newdata[i] = Q.data[(Q.front + i) % Q.queuesize];
delete[] Q.data;
Q.data = newdata;
Q.front = 0; Q.rear = Q.queuesize - 1;
Q.queuesize += Q.incresize;
return 1;
}
bool QueueEmpty(SqQueue Q) {
if (Q.front == Q.rear)
return 1;
return 0;
}
//栈--------------------------------------
typedef int SElemType;
typedef struct StackNode {
SElemType data;
struct StackNode* next;
}StackNode, * LinkStack;
bool InitStack(LinkStack& S);//初始化链栈
bool Push(LinkStack& S, SElemType e);//将元素e压入栈中
bool Pop(LinkStack& S, SElemType& e);//将首元素出栈,用元素e返回
bool StackEmpty(LinkStack S);//判断链栈是否为空
bool GetTop(LinkStack S, SElemType& e);//取链栈栈顶元素,用元素e返回
bool InitStack(LinkStack& S) {
S = NULL;
return 1;
}
bool Push(LinkStack& S, SElemType e) {
StackNode* temp = new StackNode;
if (!temp)return 0;
temp->data = e;
temp->next = S;
S = temp;
return 1;
}
bool Pop(LinkStack& S, SElemType& e) {
if (S == NULL)return 0;
StackNode* temp = S;
e = S->data;
S = S->next;
delete temp;
return 1;
}
bool StackEmpty(LinkStack S) {
if (S == NULL)
return 1;
return 0;
}
bool GetTop(LinkStack S, SElemType& e) {
if (S == NULL)return 0;
e = S->data;
return 1;
}
bool visited[MAX_VERTEX_NUM]; // 记录结点是否被访问过
void DFS(ALGraph G, int i); // 从结点i开始进行深度优先遍历
void DFSTraverse(ALGraph G); // 深度优先遍历
void BFSTraverse(ALGraph G); // 广度优先遍历
// 深度优先搜索
void DFSTraverse(ALGraph G) {
int i;
for (i = 0; i < G.vexnum; i++) // 将所有结点初始化为false,即未访问
visited[i] = false;
for (i = 0; i < G.vexnum; i++)
{
if (!visited[i]) // 从一未被访问的结点开始进行深度优先遍历
DFS(G, i);
}
}
void DFS(ALGraph G, int i) {
LinkStack S; InitStack(S); int temp;
arcNode* p;
Push(S, i); visited[i] = true; // 布置初始任务
// 此处循环流程建议对照实验样例的邻接表观察,有助于理解
while (!StackEmpty(S)) { // 过程为将一点的所有相连的未访问点入栈,并选择其中第一个点继续深入并重复上述操作,直到抵达
// 一条路径的最后一点后退栈探索另一条路径重复上述操作直到栈空结束循环
Pop(S, i); // 废物利用,让i来接收弹出的值
cout << setw(3) << G.AdjList[i].data; // 上述过程中,选择一点继续深入操作所提到的点就是整体深度优先遍历访问的中间点
for (p = G.AdjList[i].adjArc; p; p = p->nextArc) { // 将与此时p指向点相连的所有未访问点全部入栈并标为访问过
temp = p->ajdVex;
if (visited[temp] == false) {
visited[temp] = true;
Push(S, temp);
}
}//for
}//while
}
// 广度优先搜索
void BFSTraverse(ALGraph G) {
SqQueue Q; InitQueue(Q, G.vexnum); // 附设循环队列Q
arcNode* p, q;
int temp;// 用于接收临时数据
for (int i = 0; i < G.vexnum; i++) // 将所有结点初始化为false,即未访问
visited[i] = false;
for (int i = 0; i < G.vexnum; i++)
if (!visited[i]) { // 若已被访问过,则不执行
visited[i] = true;
EnQueue(Q, i); // i入队列
while (!QueueEmpty(Q)) {
DeQueue(Q, temp); // 队头元素出队并用temp接收
cout << setw(3) << G.AdjList[temp].data;
for (arcNode* p = G.AdjList[temp].adjArc; p; p = p->nextArc) {//将一层压入队列
if (!visited[p->ajdVex]) {
visited[p->ajdVex] = true;
EnQueue(Q, p->ajdVex);
}
}
}
}
}
int main() {
// 邻接矩阵的无向图
UnGraph unG;
// 邻接表的有向图
AdjGraph G;
// 邻接表的无向图
ALGraph G2;
//EdgeNode* p;
int num;
cout << "1.邻接矩阵表示法,构造一个无向网" << endl;
cout << "2.键盘输入数据,建立一个有向图的邻接表" << endl;
cout << "3.输出该邻接表" << endl;
cout << "4.键盘输入数据,建立一个无向图的邻接表" << endl;
cout << "5.采用邻接表存储实现无向图的深度优先非递归遍历" << endl;
cout << "6.采用邻接表存储实现无向图的广度优先遍历" << endl;
cout << "7.退出";
cout << endl;
while (true)
{
cout << "请输入您要选择的计算: " << endl;
cin >> num;
switch (num)
{
case 1: // 邻接矩阵表示法,构造一个无向网
{
cout << "邻接矩阵表示法,构造一个无向网" << endl;
creatUnGraph(unG);
printUnG(unG);
cout << endl;
}break;
case 2: // 键盘输入数据,建立一个有向图的邻接表
{
cout << "键盘输入数据,建立一个有向图的邻接表" << endl;
CreatGraph(G);
cout << endl;
}break;
case 3: // 输出该邻接表
{
cout << "该邻接表为:" << endl;
ShowGraph(G);
}break;
case 4: // 键盘输入数据,建立一个无向图的邻接表
{
cout << "键盘输入数据,建立一个无向图的邻接表" << endl;
cout << "*****构造无向图(邻接表)*****" << endl;
CreateAG(G2);
cout << "*******该图的邻接表为:*******" << endl;
PrintALGraph(G2);
cout << endl;
}break;
case 5: // 采用邻接表存储实现无向图的深度优先非递归遍历
{
cout << "邻接表存储的无向图的深度优先非递归遍历:" << endl;
cout << "*******深度优先搜索*******" << endl;
DFSTraverse(G2);
cout << endl;
}break;
case 6: // 采用邻接表存储实现无向图的广度优先遍历
{
cout << "邻接表存储的无向图的广度优先遍历:" << endl;
cout << "*******广度优先搜索*******" << endl;
BFSTraverse(G2);
cout << endl;
}break;
case 7:
{
cout << "退出成功!" << endl;
system("pause");
return 0;
}break;
default:
{
cout << "输入有误!请重新输入!" << endl;
}
}
}
system("pause");
return 0;
}一、实验目的
1. 掌握图的存储思想及其存储实现
2.掌握图的深度、广度优先遍历算法思想及其程序实现
3.掌握图的常见应用算法的思想及其程序实现
二、问题分析及数据结构设计
1. 问题分析:
采用邻接矩阵表示法,构造一个无向网;实现从键盘输入数据,建立一个有向图的邻接表并输出;采用邻接表存储实现无向图的深度优先和广度优先的非递归遍历。需要我们掌握图的两种存储结构:邻接表和邻接矩阵,分别用链表和数组进行存储。需要掌握深度优先和广度优先的遍历思想,分别用栈和队列进行缓存数据。
2. 数据结构设计:
顶点最大个数【MAX_VERTEX_NUM 10】
无向图【UnGraph】
顶点集【Vertex[MAX_VERTEX_NUM] 】:整型一维数组
邻接矩阵【arc[MAX_VERTEX_NUM][MAX_VERTEX_NUM] 】:整型二维数组
顶点个数【vexNum】:整型
边数【eNum】:整型
顶点数据类型【VerTexData】:字符型
边结点【arcNode】
目标结点【ajdVex】:整型
下一条边的指针【nextArc】
顶点结点【VerTexNode】
顶点值【data】:字符型
顶点的第一条边【adjArc】
有向图【AdjGraph】
邻接表【VexList[MAX_VERTEX_NUM] 】
邻接表【AdjList[MAX_VERTEX_NUM] 】
邻接矩阵用数组实现,邻接表用链表实现。广度遍历用队列实现,深度遍历用栈实现。
三、算法设计(伪代码表示)
1. 输入字符序列 创建二叉链表
Function createUnGraph(UnGraph& unG)
Begin
WHILE ture
输入顶点个数VexNum
IF 顶点个数 > 0 && 顶点个数 < 10
输入值 = 顶点个数
ELSE
重新输入
输入边的条数eNum
输入顶点信息 存入顶点数组Vertex
初始化邻接矩阵二维数组arc所有元素为0
输入边(Vi, Vj)的下标i, j及权重w
存入邻接矩阵二维数组arc[i][j]
置邻接矩阵对称元素相等arc[i][j] = arc[j][i]
End
2. 创建有向图的邻接表
Function createGraph(AdjGraph& G)
Begin
输入顶点数vexNum、边数eNum
输入顶点信息 存入链表VexList
初始化顶点第一条边adjArc = NULL
输入每一条边的头head、尾tail
创建新边结点指针p
p->目标顶点 = 边尾tail点
p->下一条边 = 边头head点头指针adjArc
边头head点头指针adjArc = p
End
3. 输出有向图的邻接表
Function showGraph(AdjGraph& G)
Begin
For i = 0 --> G的点数
输出顶点i的data
边指针p = 顶点i的首边adjArc
WHILE p != NULL
输出 p->目标结点
P = p->下一条边
End
4. 在图中查找顶点v 存在则返回下标 否则返回-1
Function LocateVex(ALGraph G, char v)
Begin
For int i = 0 --> G的点数
IF 点i的data == v
Return i
ELSE
Retutn -1
End
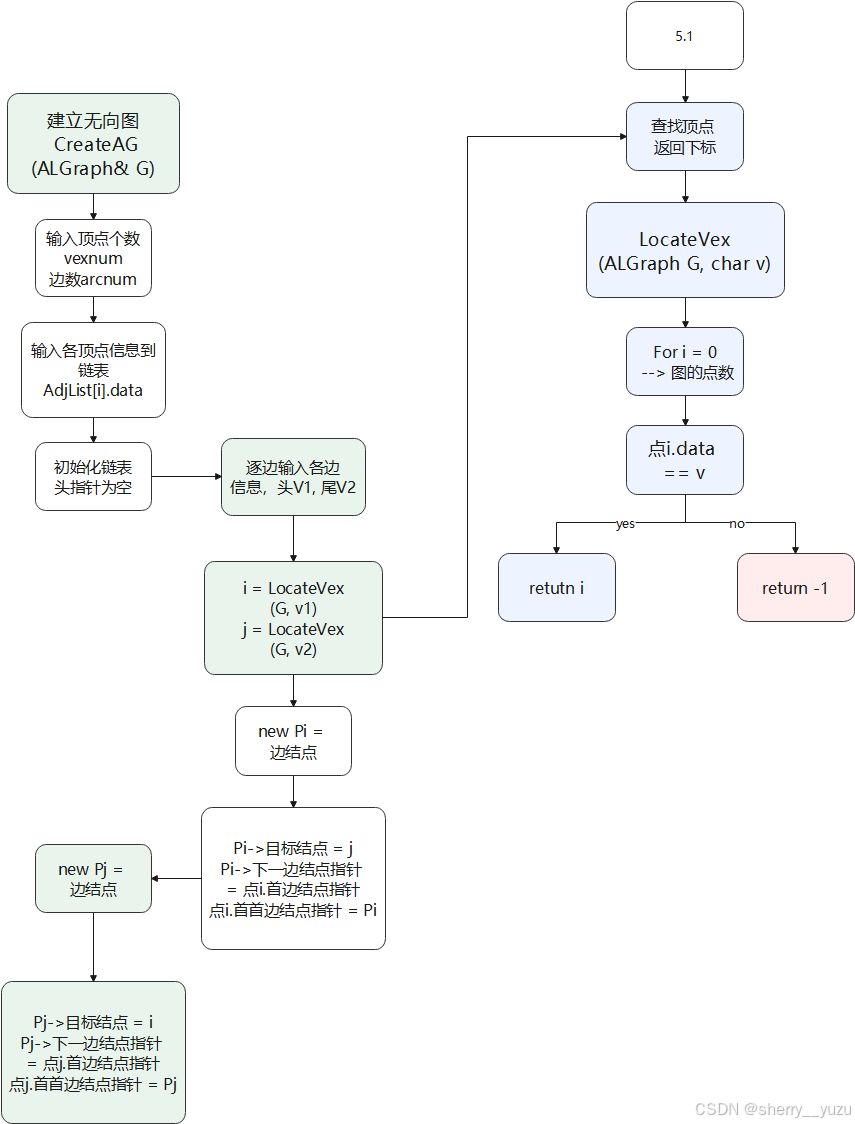
5. 建立无向图的邻接表
Function CreateAG(ALGraph& G)
Begin
输入顶点数、边数
For int i = 0 --> 顶点数
依次输入顶点信息
初始化链表头指针 = NULL
For int k = 0 -> 边数
输入边头、尾
I = 头在链表中下标
J = 尾在链表中下标
New 边指针Pi
Pi->目标结点 = j
Pi->下一条边指针 = 点i首边指针
点i首边指针 = Pi
New 边指针Pj
Pj->目标结点 = i
Pj->下一条边指针 = 点i首边指针
点i首边指针 = Pj
End
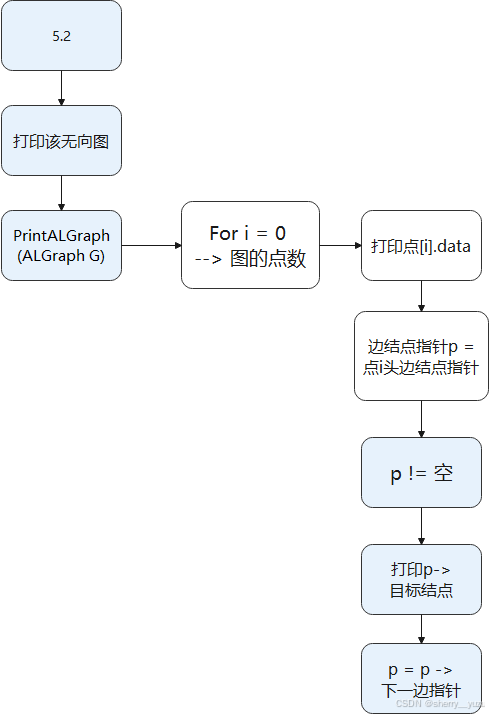
6. 输出无向图的邻接表
Function PrintALGraph(ALGraph& G)
Begin
For int i = 0 --> 图的点数
输出点i的data
边结点指针 = 点i的首边指针
WHILE p != NULL
输出p->目标结点
p = p->下一条边指针
End
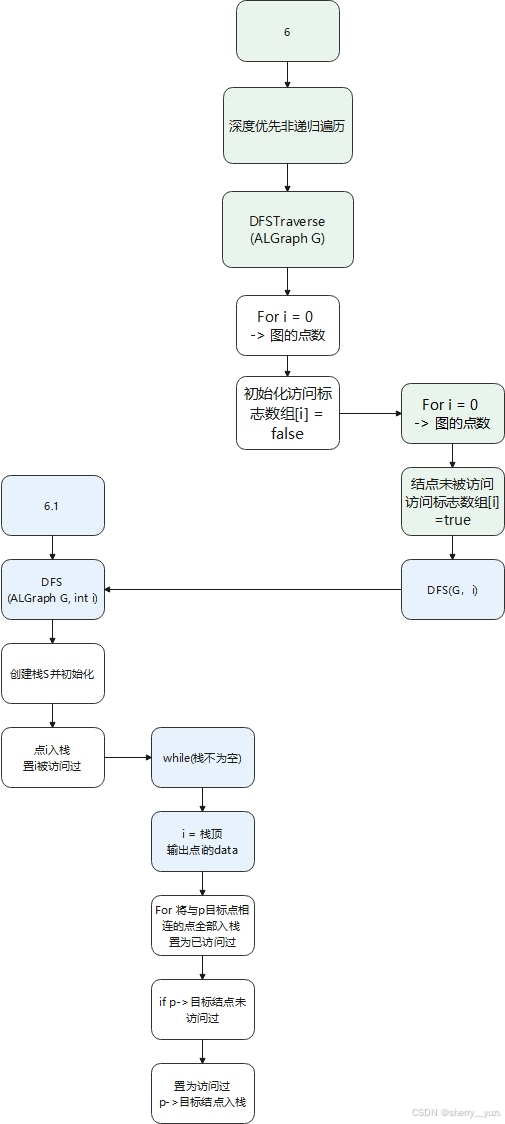
7. 深度优先遍历
Function DFS(ALGraph& G)
Begin
For int i = 0 --> 图的点数
记录结点是否被访问过的数组visited[i] = false
For int i = 0 --> 图的点数
IF !visited[i]结点未访问过
建立栈S
初始化栈
点i入栈
Visited[i] = true
WHILE 栈 != NULL
I = 栈顶出栈
输出点i的data
For p = 点i的首边指针;p;p = p->下一边指针
Temp = p->目标结点
IF visited[temp] == false
visited[temp] == true
Temp入栈
End
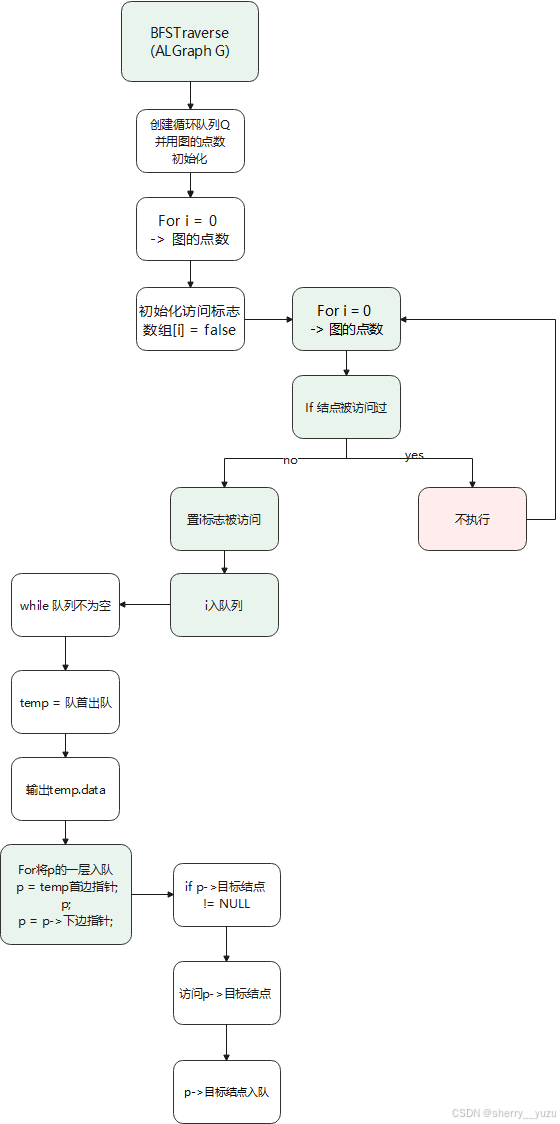
8. 广度优先遍历
Function BFS(ALGraph& G)
Begin
建立队列Q
以图的点数初始化Q
For int i = 0 --> 图的点数
记录结点是否被访问过的数组visited[i] = false
For int i = 0 --> 图的点数
IF !visited[i] 结点未访问过
visited[i] = true
点i入队列
WHILE 队列 != NULL
temp = 队首出队
输出点temp的data
For 边指针p = 点temp首边指针;p; p = p->下一边指针
IF !Visited[p->目标结点]
Visited[p->目标结点] = true
p->目标结点入队列
End
四、功能模块程序流程图
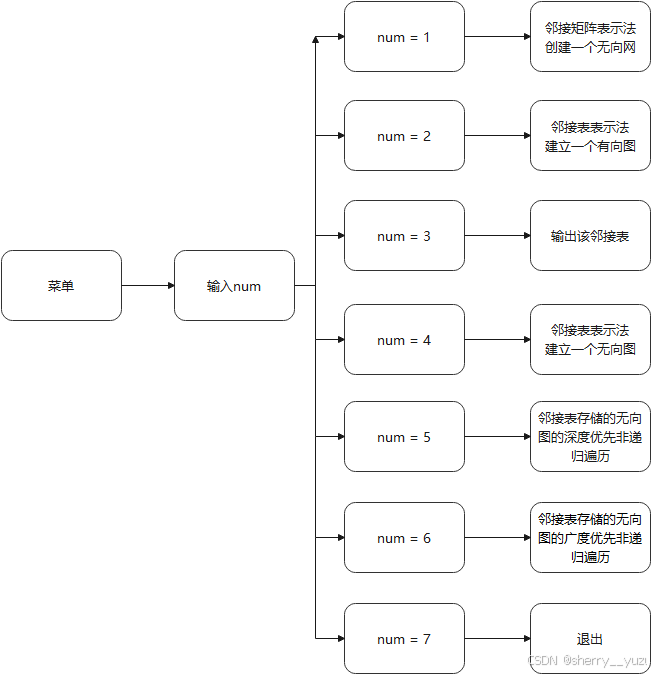
1. 菜单
说明:菜单功能首先提示用户输入数字。
输入数字1,代表邻接矩阵表示法,构造一个无向网,提示用户请输入顶点个数,边的条数,各顶点信息,各边的下标及权值w,以此建立邻接矩阵存储的无向网;
输入数字2,代表键盘输入数据,建立一个有向图的邻接表,提示用户输入图的顶点数和边数,各顶点信息,各边的下标,以此建立邻接表存储的有向图;
输入数字3,提示输出的结果为“有向图的邻接表”;
输入数字4,代表键盘输入数据,建立一个无向图的邻接表,提示用户输入图的顶点数和边数,各顶点信息,各边的下标,以此建立邻接表存储的无向图并打印;
输入数字5,提示输出的结果为“邻接表存储的无向图的深度优先非递归遍历”;
输入数字6,提示输出的结果为“邻接表存储的无向图的广度优先遍历”;
输入数字7,系统退出,提示用户“退出成功!”;
输入其他数字,提示用户"输入有误!请重新输入!"。
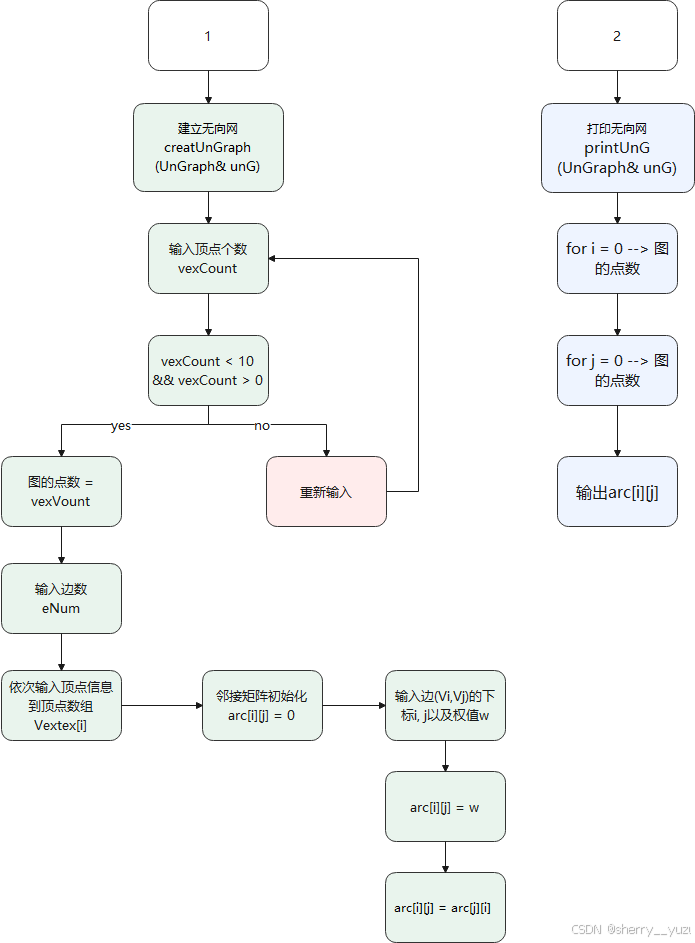
2. 邻接矩阵表示法创建一个无向网
说明:该函数目的为建立邻接矩阵存储的无向网,提醒用户输入顶点个数,边的条数,各顶点信息,各边的下标及权值w,以此建立邻接矩阵存储的无向网。
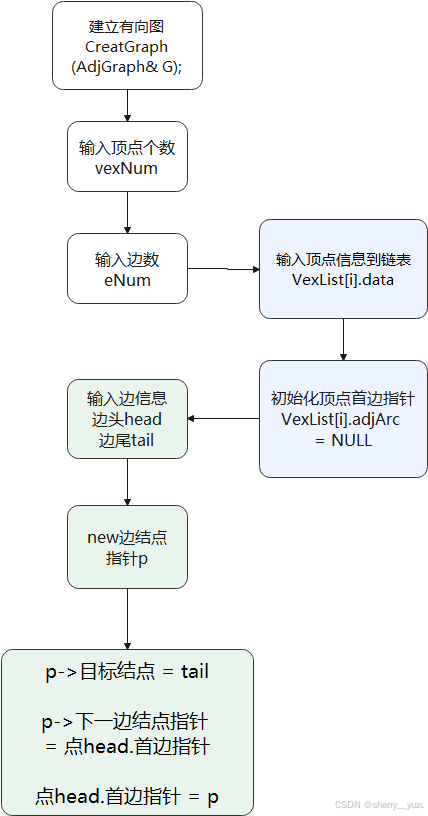
3. 邻接表表示法建立一个有向图
说明:该函数目的为建立邻接表存储的有向图,提醒用户输入顶点个数,边的条数,各顶点信息,各边的下标,以此建立邻接表存储的有向图。
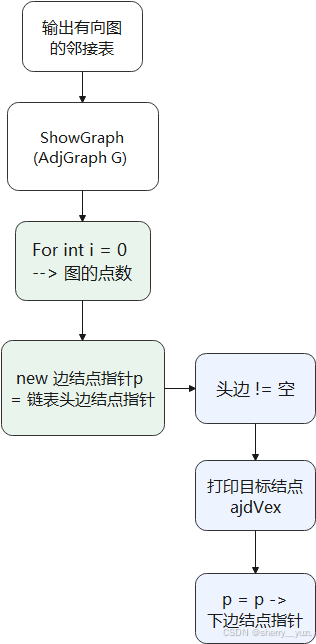
4. 输出有向图的邻接表
说明:该函数目的为输出邻接表存储的有向图,提醒用户输出的结果为邻接表存储的有向图。
5. 邻接表表示法建立一个无向图
说明:该函数目的为建立邻接表存储的无向图,提醒用户输入顶点个数,边的条数,各顶点信息,各边的下标,以此建立邻接表存储的无向图并打印,提示用户输出的结果为邻接表存储的无向图。
6. 邻接表存储的无向图的深度优先非递归遍历
说明:该函数目的为对邻接表存储的无向图的深度优先非递归遍历,提示用户输出的结果为邻接表存储的无向图的深度优先非递归遍历。
7. 邻接表存储的无向图的广度优先非递归遍历
说明:该函数目的为对邻接表存储的无向图的广度优先非递归遍历,提示用户输出的结果为邻接表存储的无向图的广度优先非递归遍历。
四、实验结果
1. 菜单:
分析:该菜单通过序号1-7来实现不同的有关图的功能,通过提示用户“请输入您要选择的计算”,来引导用户输入1-7的数字来获取想要的结果。
输入数字1,代表邻接矩阵表示法,构造一个无向网;
输入数字2,代表键盘输入数据,建立一个有向图的邻接表;
输入数字3,提示输出的结果为“有向图的邻接表”;
输入数字4,代表键盘输入数据,建立一个无向图的邻接表并打印;
输入数字5,提示输出的结果为“邻接表存储的无向图的深度优先非递归遍历”;
输入数字6,提示输出的结果为“邻接表存储的无向图的广度优先遍历”;
输入数字7,系统退出,提示用户“退出成功!”;
输入其他数字,提示用户"输入有误!请重新输入!"。
2. 邻接矩阵表示法,构造一个无向网:
分析:输入数字1后进入该邻接矩阵表示法,构造一个无向网的功能。首先提示用户输入顶点个数,边的个数,各顶点值,各边下标及权值,最后输出该无向网的邻接表。接着提示用户继续选择想要的计算。
3. 键盘输入数据,建立一个有向图的邻接表:
分析:输入数字2后进入该键盘输入数据,建立一个有向图的邻接表的功能。首先提示用户输入顶点个数和边数,各顶点值,各边下标。接着提示用户继续选择想要的计算,用户可以通过输入3来查看该有向图的邻接表的打印结果。
4. 打印有向图的邻接表:
分析:输入数字2后进入该打印有向图的邻接表的功能。首先提示用户该邻接表为,表示刚刚建立的有向图的邻接表的结果。经查看与输入2时建立的邻接表应有的输出结果一致。接着提示用户继续选择想要的计算。
5. 键盘输入数据,建立一个无向图的邻接表并打印:
分析:输入数字4后进入该键盘输入数据,建立一个无向图的邻接表并打印的功能。首先提示用户输入顶点个数和边数,各顶点值,各边下标。接着提示用户该图的邻接表为,表示刚刚建立的无向图的邻接表的结果。经查看刚刚建立的邻接表应有的输出结果一致。接着提示用户继续选择想要的计算。
6. 邻接表存储的无向图的深度优先非递归遍历:
分析:输入数字5后进入该邻接表存储的无向图的深度优先非递归遍历的功能。提示用户深度优先搜索的结果为,表示刚刚建立的无向图的深度优先搜索的结果。经查看刚刚建立的邻接表应有的输出结果一致。接着提示用户继续选择想要的计算。
7. 邻接表存储的无向图的广度优先遍历:
分析:输入数字5后进入该邻接表存储的无向图的深度优先非递归遍历的功能。提示用户深度优先搜索的结果为,表示刚刚建立的无向图的深度优先搜索的结果。经查看刚刚建立的邻接表应有的输出结果一致。接着提示用户继续选择想要的计算。
8. 退出:
分析:输入数字7后进入该退出系统的功能,提示用户退出成功。退出成功后,不会再出现提示用户继续输入想要选择的运算。
9. 输入其他数字;
分析:输入其他数字7后进提示用户输入有误,请重新输入。并再次提示用户继续输入想要选择的运算。
五、算法分析
1. 邻接矩阵表示法,构造一个无向网:
通过一维数组存储顶点信息,二维数组各边的权值以表示各点的关系。因为是无向网,所以最后令二维数组对称即邻接矩阵对称。
2. 键盘输入数据,建立一个有向图的邻接表:
用链表存储各点的链接边的信息。令边结点指针的目标结点为边尾,边结点指针的下一条边结点指针为边头的首边结点指针,再令边头的首边结点指针为该边。
3. 打印有向图的邻接表:
找完一个顶点的所有链接边,再开始找下一个顶点的所有链接边。
首先输出第一个顶点i的data,再令一个新的边结点指针为i的首边结点指针,如果i的首边存在,则输出该边的尾点,再令该边尾该边的下一边结点指针,重复上述操作。
4. 键盘输入数据,建立一个无向图的邻接表:
用链表存储各点的链接边的信息。
先通过边头和边尾的点找到它们在链表中所处的下标位置,再类似于单链表的头插法进行插入,令边头结点指针的目标结点为边尾所在下标,边结点指针的下一条边结点指针为边头的首边结点指针,再令边头的首边结点指针为该边。
因为为无向图,所以令边尾所在结点重复上述操作以指向边头结点,更新边尾结点的指针。
5. 邻接表存储的无向图的深度优先非递归遍历:
通过一个是否被访问过的标志数组来选择是否要访问该顶点。
首先初始化该访问标志所有元素为false代表所有元素都未被访问,然后再for循环一个个访问未被访问过的顶点,进行深度遍历。
利用栈将一点所有相连且未访问过的点入栈,直到这条路径访问完,则继续探索另一条路径,直到栈空结束。
6. 邻接表存储的无向图的广度优先遍历:
通过一个是否被访问过的标志数组来选择是否要访问该顶点。
首先初始化该访问标志所有元素为false代表所有元素都未被访问,然后再for循环一个个访问未被访问过的顶点,进行广度遍历。利用队列将一点所在的一层链接的边结点全部入队。
六、操作说明
编译后首先出现一个菜单,1-7有文字信息描述图的相关算法,提示用户输入1-7之间的数字。输入数字1,代表邻接矩阵表示法,构造一个无向网;输入数字2,代表键盘输入数据,建立一个有向图的邻接表;输入数字3,提示输出的结果为“有向图的邻接表”;输入数字4,代表键盘输入数据,建立一个无向图的邻接表并打印;输入数字5,提示输出的结果为“邻接表存储的无向图的深度优先非递归遍历”;输入数字6,提示输出的结果为“邻接表存储的无向图的广度优先遍历”;输入数字7,系统退出,提示用户“退出成功!”;输入其他数字,提示用户"输入有误!请重新输入!"。