如何加速矩阵乘法——优化GEMM (CPU单线程篇)

矩阵乘法GEMM(General matrix multiply)是一个被广泛使用的基础算法，各种领域都需要应用，例如神经网络的核心计算任务就是矩阵乘法，交易中的各种信号计算也可能用到矩阵乘法。因此矩阵乘法的效率是极其关键的。

关于如何优化矩阵乘法，我准备写一个较短的系列博文，包括CPU单线程篇、CPU多线程篇、GPU篇。原本计划还有一个稀疏矩阵乘法篇，由于这学期毕业前也没有时间把GPU篇做到满意，因此，稀疏矩阵篇就没了，GPU篇也很不完整。如果日后有时间且有那冲动可能会补上（大概率没有）。

这是矩阵乘法优化第一篇，CPU单线程篇。

矩阵乘法对于同样的抽象算法，不同的优化带来的性能差异极大，现代的部分CPU上最朴素的矩阵乘法实现和最优实现甚至可以有百倍以上的性能差距，这比一些有更低时间复杂度的矩阵乘法算法的优化效果都有效。而这都是针对现代CPU的体系结构作出的针对性优化带来的，SIMD向量指令更是增加了CPU的处理大批量数据时的效率。在本文中，我们将介绍如何针对CPU进行单线程GEMM实现的优化。

这个系列的代码可以在https://github.com/renzibei/optimize-gemm中找到，部分测试代码来自于《并行计算基础》课程。。

矩阵的内存格式

要说清矩阵乘法，那么首先要统一矩阵的表示。对于C系语言而言，矩阵可以简单地用二维数组表示，例如矩阵中第i行第j列可以表示为。但是在系统底层的内存中，只有连续的储存空间，编译器会将高级语言的二维数组的访存转换为对一维内存地址的访问。将二维坐标映射成一维坐标有很多方法，直接的有两种：行主序(row-major order)和列主序(column-major order)1。简单地说，对于前面提到的元素，如果要映射为一维数组，既可以用行主序的的方式，如果一行的内存元素有个，则对应为；如果使用列主序的方式，如果一列的内存元素有个，则对应为。之所以这里说内存元素有个而不说一行有个元素或者说一列有个元素，是有原因的，例如，对于行主列的储存方式而言，矩阵一行有个元素，但是矩阵一行占用的内存不一定是个，可能由于内存对齐的原因，一行占用了个内存，且。因此，表示矩阵储存时，需要知道矩阵的储存格式是行主序还是列主序，还需要指出的值。对于C系编程语言而言，一般二维数组使用行主序的储存方式。对于Fortran语言和与其渊源颇深的BLAS框架，一般都使用列主序的储存方式。

本文和相关代码中都使用列主序的方式表示矩阵元素，即矩阵A的第i行第j列元素对应为。另外在代码中为了方便，很多地方，因此也可能直接表示成

测试方法

下文的讨论将围绕计算这个目标展开，其中A为M行K列矩阵，B为K行N列矩阵，C为M行N列矩阵。测试中的矩阵元素类型为单精度Float。

本文测试中的CPU使用的是ARM架构的鲲鹏920，主频2.6GHz，具有128bit SIMD寄存器与向量指令集。每核有私有的512KB L2 Cache。

本文中我们进行的性能测试的数据都是在M=N=K的情况下，测试N从127到1281的多个数据规模的性能，评价的指标为每秒浮点运算次数Flops

我们使用OpenBLAS框架作为优化的目标，OpenBLAS针对不同的CPU架构写了针对性的优化代码，其GEMM算法的优化程度基本属于最高的一个级别中（Intel的芯片上Intel自家的科学计算库性能更高）。在我们的测试环境中，OpenBLAS的平均浮点性能在32Gflops左右。

优化过程

在下面的优化过程中，我们都使用-O2优化，来让编译器做一些简单的自动优化，同时不会明显改变我们的优化意图。

最朴素实现的平均浮点性能为1.098 Gflops，我们最终优化后的平均浮点性能约为28.3 Gflops，距离OpenBLAS的性能还有一些距离。

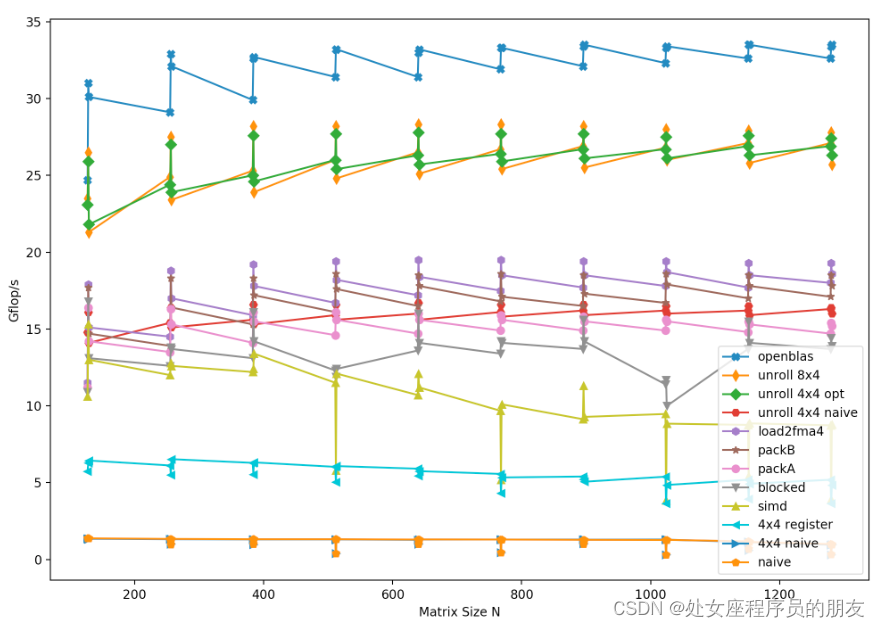
多种优化后的性能随数据规模变化关系如Figure 1所示，可以看到最终性能在数据规模够大后几乎不受数据规模影响，比较稳定。

Figure 1: 多种优化后性能随数据规模变化

前半部分优化参考了https://github.com/flame/how-to-optimize-gemm/wiki 的一些方法。

朴素实现

朴素矩阵乘法就是一个简单的算法，三层循环。对于这个矩阵乘法和加法，可以用下面的代码描述：

for (int i = 0; i < M; ++i) {
	for (int j = 0; j < N; ++j) {
		for (int k = 0; k < K; ++k) {
			C[i + j * ldc] += A[i + k * lda] * B[k + j * ldb];
		}
	}
}

这段代码非常直接，而且有一些可以直接优化的部分，例如对的累加过程可以使用一个寄存器中的变量暂存，编译器为了防止指针的Alias产生，不能自动进行这一优化。

这种naive的方法的平均性能为1.098 Gflops，这是一个相当差的性能。那么性能瓶颈在哪呢？

理论上的矩阵乘法要进行量级的乘加计算，内存数据量只有规模，内存访问次数是量级。GEMM既是计算密集型也是访存密集型的任务。如果我们的访存速度和计算速度几乎相当的话，花在访存指令上的时间应该和花在浮点计算指令上的时间相当。但是，我们知道内存的访问带宽远远小于CPU的浮点计算吞吐量，访存延迟也远高于CPU的浮点指令延迟，而CPU的Cache虽快，大小十分有限，不能塞下所有的矩阵数据。因此，朴素实现的瓶颈会在于访存指令的延迟，每个浮点计算指令都要等访存指令执行完。

那么，我们要决定我们优化的方向。我们需要解决访存带宽的问题，这个问题可以通过将矩阵分块（Blocking）的方法解决，虽然整个矩阵装不进Cache里，但是一个足够小的子矩阵还是可以的。将矩阵分块后，计算的次数和访存次数不变，但是更多的访存指令能从Cache直接获取数据，大大减小了平均访存延迟。

另外，我们可以使用SIMD向量化指令，一个指令可以操控多个数据，可以提高访存和计算吞吐率。

数据并行化的准备

为了之后的SIMD向量化，我们需要对算法的实现步骤做一些调整。例如，对于矩阵C的每一个元素的计算，朴素实现中每次只是拿矩阵A的一行去点乘矩阵B的一列。而如果我们同时算C中的4个元素，那么我们就能同时取A中的连续4行与B中的连续4列。这样连续取整块的内存是有利于后面的向量化的。

具体而言，我们每次同时计算C的4x4的16个元素，这样的话我们同时用到了A的连续4行与B的连续4列。

如果我们只是调整一下形式，不做其他优化的话，性能几乎不会有变化。现在的浮点性能为1.087 Gflops。

内层循环的核心代码如下，注意其中的对应的是4x4的小方块中的而不是整个大矩阵中的位置。

for (int k = 0; k < K; ++k) {
    C[0 + 0 * ldc] += A[0 + k * lda] * B[k + 0 * ldb];
    C[0 + 1 * ldc] += A[0 + k * lda] * B[k + 1 * ldb];
    C[0 + 2 * ldc] += A[0 + k * lda] * B[k + 2 * ldb];
    C[0 + 3 * ldc] += A[0 + k * lda] * B[k + 3 * ldb];

    C[1 + 0 * ldc] += A[1 + k * lda] * B[k + 0 * ldb];
    C[1 + 1 * ldc] += A[1 + k * lda] * B[k + 1 * ldb];
    C[1 + 2 * ldc] += A[1 + k * lda] * B[k + 2 * ldb];
    C[1 + 3 * ldc] += A[1 + k * lda] * B[k + 3 * ldb];

    C[2 + 0 * ldc] += A[2 + k * lda] * B[k + 0 * ldb];
    C[2 + 1 * ldc] += A[2 + k * lda] * B[k + 1 * ldb];
    C[2 + 2 * ldc] += A[2 + k * lda] * B[k + 2 * ldb];
    C[2 + 3 * ldc] += A[2 + k * lda] * B[k + 3 * ldb];

    C[3 + 0 * ldc] += A[3 + k * lda] * B[k + 0 * ldb];
    C[3 + 1 * ldc] += A[3 + k * lda] * B[k + 1 * ldb];
    C[3 + 2 * ldc] += A[3 + k * lda] * B[k + 2 * ldb];
    C[3 + 3 * ldc] += A[3 + k * lda] * B[k + 3 * ldb];
  }

这一部分我写的可能不是很详细，大家可以参考https://github.com/flame/how-to-optimize-gemm/wiki 的做法。

利用寄存器减少访存次数

上面的代码有一些很明显的可以减少访存次数的优化方法，例如将16个C中的元素都先用寄存器暂存，然后累加时使用寄存器，最后再写入内存。

另外，内层循环的每一次迭代中，A中的访问内存的次数为16次，B也为16次，但其实A与B都只各自访问了4个元素，因此其实也可以各用4个寄存器先加载内存，然后使用寄存器计算。

减少访存后，平均浮点性能为5.385 Gflops，这相对于之前是一个很大的提升。

内层循环的核心代码如下，

register float c00 = 0, c01 = 0, c02 = 0, c03 = 0, c10 = 0, c11 = 0, 
   c12 = 0, c13 = 0, c20 = 0, c21 = 0, c22 = 0, c23 = 0, c30 = 0, c31 = 0, c32 = 0, c33 = 0;
 register float a0i, a1i, a2i, a3i;
 register float bi0, bi1, bi2, bi3;

 float *bi0_p, *bi1_p, *bi2_p, *bi3_p;

 bi0_p = B; bi1_p = B + 1 * ldb; bi2_p = B + 2 * ldb; bi3_p = B + 3 * ldb;
 for (int i = 0; i < n; ++i) {

   a0i = A[i * lda]; a1i = A[1 + i * lda]; a2i = A[2 + i * lda]; a3i = A[3 + i * lda];
   bi0 = *bi0_p++; bi1 = *bi1_p++; bi2 = *bi2_p++; bi3 = *bi3_p++;

   c00 += a0i * bi0;
   c01 += a0i * bi1; 
   c02 += a0i * bi2;
   c03 += a0i * bi3;

   c10 += a1i * bi0;
   c11 += a1i * bi1;
   c12 += a1i * bi2;
   c13 += a1i * bi3;

   c20 += a2i * bi0;
   c21 += a2i * bi1;
   c22 += a2i * bi2;
   c23 += a2i * bi3;

   c30 += a3i * bi0;
   c31 += a3i * bi1;
   c32 += a3i * bi2;
   c33 += a3i * bi3;

 }
 C[0 + 0 * ldc] += c00;  C[0 + 1 * ldc] += c01;  C[0 + 2 * ldc] += c02;  C[0 + 3 * ldc] += c03;
 C[1 + 0 * ldc] += c10;  C[1 + 1 * ldc] += c11;  C[1 + 2 * ldc] += c12;  C[1 + 3 * ldc] += c13;
 C[2 + 0 * ldc] += c20;  C[2 + 1 * ldc] += c21;  C[2 + 2 * ldc] += c22;  C[2 + 3 * ldc] += c23;
 C[3 + 0 * ldc] += c30;  C[3 + 1 * ldc] += c31;  C[3 + 2 * ldc] += c32;  C[3 + 3 * ldc] += c33;

SIMD向量化

之前我们已经将计算的顺序进行了改变，每次计算C的4x4的方块，每个内层循环的迭代中用到了4个矩阵A的元素和4个矩阵B的元素。这是很容易进行向量化的形式。

具体到ARM架构的CPU上，我们使用Neon向量指令集，每个指令可以操控128bit即4个Float数据，正好对我们上面的代码进行并行。

向量化后平均性能为9.963 Gflops，又有了进一步的提升。

内存循环的核心代码如下，

float32x4_t c_c0, c_c1, c_c2, c_c3, a_ri, b_vi0, b_vi1, b_vi2, b_vi3;
 c_c0 = vmovq_n_f32(0.0), c_c1 = vmovq_n_f32(0.0), c_c2 = vmovq_n_f32(0.0), c_c3 = vmovq_n_f32(0.0);

 float *bi0_p, *bi1_p, *bi2_p, *bi3_p;

 bi0_p = B; bi1_p = B + 1 * ldb; bi2_p = B + 2 * ldb; bi3_p = B + 3 * ldb;
 for (int i = 0; i < n; ++i) {
   a_ri = vld1q_f32(A + i * lda);
   b_vi0 = vld1q_dup_f32(bi0_p++); b_vi1 = vld1q_dup_f32(bi1_p++); 
   b_vi2 = vld1q_dup_f32(bi2_p++); b_vi3 = vld1q_dup_f32(bi3_p++);

   c_c0 = vmlaq_f32(c_c0, a_ri, b_vi0);
   c_c1 = vmlaq_f32(c_c1, a_ri, b_vi1);
   c_c2 = vmlaq_f32(c_c2, a_ri, b_vi2);
   c_c3 = vmlaq_f32(c_c3, a_ri, b_vi3);
 }
 vst1q_f32(C + 0 * ldc, c_c0); vst1q_f32(C + 1 * ldc, c_c1);
 vst1q_f32(C + 2 * ldc, c_c2); vst1q_f32(C + 3 * ldc, c_c3);

矩阵分块 Blocking

之前的方法在数据规模变大后性能都会有较大的下降，问题在于L2 Cache大小有限，如果不停地访存很快会把L2 Cache刷满一遍。因此应该让高密度计算中的访存范围集中，使用Blocked分块的方法。采取的分块策略是A每次访问MCxKC的块，B每次访问KC x ldb的块。其中MC和KC的大小进行多次尝试决定。

我们这里的分块并不彻底，B没有完全分块，其实B也可以分成KC x NC的块，只是在这一步继续分块对Cache带来的帮助并不大，因此我们暂且只分成这样，后续会将B也完全分成小块。

分块后的平均性能为13.612 Gflops，主要带来的收益是矩阵规模提升时性能不会下降。

外层的分块过程如下，do_block函数内部的过程和之前的完整外部循环类似。

for (int k = 0; k < n; k += KC) {
    int K = min(n - k, KC);
    for (int i = 0; i < n; i += MC) {
      int M = min(n - i, MC);
      int N = n;
      do_block(M, N, K, n, n, n, A + i + k * n, B + k, C + i);
    }
}

内存重排 Packing

每次对A进行4x1的访存时，是对4行同一列元素进行的访存，但是每次循环就会跳到下一列，由于是列主序的矩阵，循环间访存不是连续的，最好将所有循环会访问的元素排到一起，可以减少跨区域访存的次数，增加数据在一条Cache Line中的概率。因此对A进行了4行元素的内存重排。

每次对B是进行1x4的访存，每次对同一行四列的元素访问，由于列主序，一次循环内的访存是不连续的，可以将4列的元素重排到一起。

对矩阵A的元素进行Packing后，平均性能为15.212 Gflops；对矩阵B的元素Packing后，平均性能为 17.139 Gflops。

进一步提高计算/访存比

之前代码的kernel部分，循环内一次计算取A的四个float，B的四个float，但是，B的每个float是用来标量乘A向量的，因此当时的做法是把B的每个float重复为1个32bitx4的向量再与A的向量相乘，核心代码如下

a_ri = vld1q_f32(A);
b_vi0 = vld1q_dup_f32(B); 
b_vi1 = vld1q_dup_f32(B + 1);
b_vi2 = vld1q_dup_f32(B + 2); 
b_vi3 = vld1q_dup_f32(B + 3);
c_c0 = vmlaq_f32(c_c0, a_ri, b_vi0);
c_c1 = vmlaq_f32(c_c1, a_ri, b_vi1);
c_c2 = vmlaq_f32(c_c2, a_ri, b_vi2);
c_c3 = vmlaq_f32(c_c3, a_ri, b_vi3);

这段代码有5次访存，4次fma（乘加指令）向量乘（mla指令和fma的效果是一样的）。

其对应汇编代码如下(删掉了一些重新排布的无关代码)，有一次单向量寄存器的load，两次双向量寄存器的load，也就是总共load了5个128bit寄存器，然后进行了4次fma计算。

4010e0:	3dc00080 	ldr	q0, [x4]
4010e8:	2d401cb0 	ldp	s16, s7, [x5]
4010ec:	2d4114a6 	ldp	s6, s5, [x5, #8]
4010f4:	4f901004 	fmla	v4.4s, v0.4s, v16.s[0]
4010fc:	4f871003 	fmla	v3.4s, v0.4s, v7.s[0]
401100:	4f861002 	fmla	v2.4s, v0.4s, v6.s[0]
401104:	4f851001 	fmla	v1.4s, v0.4s, v5.s[0]

我们粗略地计算乘加指令和load指令的比例的话，（ldp这种一次load两个寄存器的指令用的周期应该略低于只load一个寄存器的指令，但是我们还是算其为2个load指令），为4/5 = 0.8

这对于矩阵乘法而言，并不是很好的计算访存比，对于矩阵乘法，总共需要的从内存中转移到寄存器的访存次数为，乘加计算为，

计算访存比是，问题在于我们的寄存器数量有限，不可能一次load后一直使用，因此我们只能尽可能地多使用已有的寄存器。

对于我上面写的代码，一个很容易的优化是，我只需要B的4个float，理论上一个load指令就可以全部加载进来，只是后面的普通fma指令要变成fma_lane指令。

新的核心代码如下

a_ri = vld1q_f32(A + i * lda);
b_vi0 = vld1q_f32(B);
c_c0 = vfmaq_laneq_f32(c_c0, a_ri, b_vi0, 0);
c_c1 = vfmaq_laneq_f32(c_c1, a_ri, b_vi0, 1);
c_c2 = vfmaq_laneq_f32(c_c2, a_ri, b_vi0, 2);
c_c3 = vfmaq_laneq_f32(c_c3, a_ri, b_vi0, 3);

汇编指令如下，原来的1个ldr指令2个ldp指令变成了2个ldr指令，只load了2次SIMD寄存器，乘加指令与load指令的计算/访存比变为4 / 2 = 2.0

4010e0:	3cc104a1 	ldr	q1, [x5], #16
4010e4:	3dc00080 	ldr	q0, [x4]
4010f0:	4f811005 	fmla	v5.4s, v0.4s, v1.s[0]
4010f4:	4fa11004 	fmla	v4.4s, v0.4s, v1.s[1]
4010f8:	4f811803 	fmla	v3.4s, v0.4s, v1.s[2]
4010fc:	4fa11802 	fmla	v2.4s, v0.4s, v1.s[3]

优化后的平均性能为17.847 Gflops，性能有小部分提升。

循环展开，A、B一次加载4x4

之前我们的kernel一次只加载了A的4x1和B的1x4的元素，但是考虑到每次循环都有一次add和cmp指令，以及充分利用流水线的思想，我们可以把kernel的循环展开，一次加载4个A的4x1和4个B的1x4的元素，这样就变为一次加载4x4的A中元素和4x4的B中元素，代码如下

a_c0_i0 = vld1q_f32(A + i * 4);
a_c0_i1 = vld1q_f32(A + i * 4 + 4);
a_c0_i2 = vld1q_f32(A + i * 4 + 8);
a_c0_i3 = vld1q_f32(A + i * 4 + 12);
b_vi0_0 = vld1q_f32(B + 0);
b_vi1_0 = vld1q_f32(B + 4);
b_vi2_0 = vld1q_f32(B + 8);
b_vi3_0 = vld1q_f32(B + 12);

c_c0 = vaddq_f32(vaddq_f32(vmulq_laneq_f32(a_c0_i0, b_vi0_0, 0), vmulq_laneq_f32(a_c0_i1, b_vi1_0, 0)) ,  vaddq_f32(vmulq_laneq_f32(a_c0_i2, b_vi2_0, 0), vfmaq_laneq_f32(c_c0, a_c0_i3, b_vi3_0, 0)));
    
c_c1 = vaddq_f32(vaddq_f32(vmulq_laneq_f32(a_c0_i0, b_vi0_0, 1), vmulq_laneq_f32(a_c0_i1, b_vi1_0, 1)) ,  vaddq_f32(vmulq_laneq_f32(a_c0_i2, b_vi2_0, 1), vfmaq_laneq_f32(c_c1, a_c0_i3, b_vi3_0, 1)));
    
c_c2 = vaddq_f32(vaddq_f32(vmulq_laneq_f32(a_c0_i0, b_vi0_0, 2), vmulq_laneq_f32(a_c0_i1, b_vi1_0, 2)) ,  vaddq_f32(vmulq_laneq_f32(a_c0_i2, b_vi2_0, 2), vfmaq_laneq_f32(c_c2, a_c0_i3, b_vi3_0, 2)));
    
c_c3 = vaddq_f32(vaddq_f32(vmulq_laneq_f32(a_c0_i0, b_vi0_0, 3), vmulq_laneq_f32(a_c0_i1, b_vi1_0, 3)) ,  vaddq_f32(vmulq_laneq_f32(a_c0_i2, b_vi2_0, 3), vfmaq_laneq_f32(c_c3, a_c0_i3, b_vi3_0, 3)));

转换为汇编如下，16个乘加指令，4个fadd指令，1个ldp指令，6个ldur指令，总共load了8个SIMD寄存器，计算/访存比为2.5，但是20个乘/加指令中只有16个是必要的，因此这里的性能反而会下降。

4011d0:	ad40c0a0 	ldp	q0, q16, [x5, #16]
4011d4:	910100a5 	add	x5, x5, #0x40
4011d8:	3cdf00a7 	ldur	q7, [x5, #-16]
4011dc:	91010021 	add	x1, x1, #0x40
4011e0:	3cdd0025 	ldur	q5, [x1, #-48]
4011e4:	3cdf0026 	ldur	q6, [x1, #-16]
4011e8:	4f8098b1 	fmul	v17.4s, v5.4s, v0.s[2]
4011ec:	4f8090b3 	fmul	v19.4s, v5.4s, v0.s[0]
4011f0:	4f8710c4 	fmla	v4.4s, v6.4s, v7.s[0]
4011f4:	4fa710c3 	fmla	v3.4s, v6.4s, v7.s[1]
4011f8:	4f8718c2 	fmla	v2.4s, v6.4s, v7.s[2]
4011fc:	4fa718c1 	fmla	v1.4s, v6.4s, v7.s[3]
401200:	3cde0027 	ldur	q7, [x1, #-32]
401204:	4fa090b2 	fmul	v18.4s, v5.4s, v0.s[1]
401208:	4fa098a0 	fmul	v0.4s, v5.4s, v0.s[3]
40120c:	4f9010e4 	fmla	v4.4s, v7.4s, v16.s[0]
401210:	4fb010e3 	fmla	v3.4s, v7.4s, v16.s[1]
401214:	4f9018e2 	fmla	v2.4s, v7.4s, v16.s[2]
401218:	4fb018e1 	fmla	v1.4s, v7.4s, v16.s[3]
40121c:	4eb11e27 	mov	v7.16b, v17.16b
401220:	3cdc00a6 	ldur	q6, [x5, #-64]
401224:	eb0200bf 	cmp	x5, x2
401228:	3cdc0025 	ldur	q5, [x1, #-64]
40122c:	4f8610b3 	fmla	v19.4s, v5.4s, v6.s[0]
401230:	4fa610b2 	fmla	v18.4s, v5.4s, v6.s[1]
401234:	4f8618a7 	fmla	v7.4s, v5.4s, v6.s[2]
401238:	4fa618a0 	fmla	v0.4s, v5.4s, v6.s[3]
40123c:	4e33d484 	fadd	v4.4s, v4.4s, v19.4s
401240:	4e32d463 	fadd	v3.4s, v3.4s, v18.4s
401244:	4e27d442 	fadd	v2.4s, v2.4s, v7.4s
401248:	4e20d421 	fadd	v1.4s, v1.4s, v0.4s

代码的平均性能只有15.969 Gflops

重新排布指令，结合乘加

上面的代码中的求和部分有一些是不必要的，只要写成部分和，循环结束后再规约求和，另外还有一些求和可以利用fma指令在计算乘法时顺便求出，因此我们重新排布了指令如下

a_c0_i0 = vld1q_f32(A + i * 4);
a_c0_i1 = vld1q_f32(A + i * 4 + 4);
a_c0_i2 = vld1q_f32(A + i * 4 + 8);
a_c0_i3 = vld1q_f32(A + i * 4 + 12);
b_vi0_0 = vld1q_f32(B + 0);
b_vi1_0 = vld1q_f32(B + 4);
b_vi2_0 = vld1q_f32(B + 8);
b_vi3_0 = vld1q_f32(B + 12);
temp_v0 = vfmaq_laneq_f32(c_c0, a_c0_i0, b_vi0_0, 0);
c_c0 = vfmaq_laneq_f32(temp_v0, a_c0_i1, b_vi1_0, 0);
temp_v3 = vfmaq_laneq_f32(c_c1, a_c0_i1, b_vi1_0, 1);
c_c1 = vfmaq_laneq_f32(temp_v3, a_c0_i0, b_vi0_0, 1);
temp_v0 = vfmaq_laneq_f32(c_c2, a_c0_i0, b_vi0_0, 2);
c_c2 = vfmaq_laneq_f32(temp_v0, a_c0_i1, b_vi1_0, 2);
temp_v3 = vfmaq_laneq_f32(c_c3, a_c0_i1, b_vi1_0, 3);
c_c3 = vfmaq_laneq_f32(temp_v3, a_c0_i0, b_vi0_0, 3);


temp_v0 = vfmaq_laneq_f32(part1_c0, a_c0_i2, b_vi2_0, 0);
part1_c0 = vfmaq_laneq_f32(temp_v0, a_c0_i3, b_vi3_0, 0);
temp_v3 = vfmaq_laneq_f32(part1_c1, a_c0_i3, b_vi3_0, 1);
part1_c1 = vfmaq_laneq_f32(temp_v3, a_c0_i2, b_vi2_0, 1);
temp_v0 = vfmaq_laneq_f32(part1_c2, a_c0_i2, b_vi2_0, 2);
part1_c2 = vfmaq_laneq_f32(temp_v0, a_c0_i3, b_vi3_0, 2);
temp_v3 = vfmaq_laneq_f32(part1_c3, a_c0_i3, b_vi3_0, 3);
part1_c3 = vfmaq_laneq_f32(temp_v3, a_c0_i2, b_vi2_0, 3);

生成的汇编如下，浮点相关的全为乘加指令，4个ldp指令load 8个寄存器，16个fma指令，计算访存比为2.0

4011e0:	ad405854 	ldp	q20, q22, [x2]
4011e4:	ad405cb5 	ldp	q21, q23, [x5]
4011e8:	ad414850 	ldp	q16, q18, [x2, #32]
4011ec:	91010042 	add	x2, x2, #0x40
4011f0:	ad414cb1 	ldp	q17, q19, [x5, #32]
4011f4:	910100a5 	add	x5, x5, #0x40
4011f8:	4f951287 	fmla	v7.4s, v20.4s, v21.s[0]
4011fc:	eb0100bf 	cmp	x5, x1
401200:	4f951a83 	fmla	v3.4s, v20.4s, v21.s[2]
401204:	4fb712c5 	fmla	v5.4s, v22.4s, v23.s[1]
401208:	4fb71ac1 	fmla	v1.4s, v22.4s, v23.s[3]
40120c:	4f911206 	fmla	v6.4s, v16.4s, v17.s[0]
401210:	4f911a02 	fmla	v2.4s, v16.4s, v17.s[2]
401214:	4fb31244 	fmla	v4.4s, v18.4s, v19.s[1]
401218:	4fb31a40 	fmla	v0.4s, v18.4s, v19.s[3]
40121c:	4f9712c7 	fmla	v7.4s, v22.4s, v23.s[0]
401220:	4f971ac3 	fmla	v3.4s, v22.4s, v23.s[2]
401224:	4fb51285 	fmla	v5.4s, v20.4s, v21.s[1]
401228:	4fb51a81 	fmla	v1.4s, v20.4s, v21.s[3]
40122c:	4f931246 	fmla	v6.4s, v18.4s, v19.s[0]
401230:	4f931a42 	fmla	v2.4s, v18.4s, v19.s[2]
401234:	4fb11204 	fmla	v4.4s, v16.4s, v17.s[1]
401238:	4fb11a00 	fmla	v0.4s, v16.4s, v17.s[3]

平均性能为25.952 Gflops，开了-O3优化后平均性能为26.124Gflops，峰值性能为27.8 Gflops

再增加循环展开层数

之前一次加载16个A中的元素，如果一次加载32个A中的float，进行8x4的一次load，则性能还能有微弱提升

平均性能为26.22 Gflops，峰值性能为28.3 Gflops

其实接下来还有更多优化方法，例如Prefetch技术，在本轮迭代的计算中就先fetch下一轮迭代会用到的数据，充分利用流水线隐藏延迟，能够进一步提高性能。但由于这些技术高度和具体CPU架构相关且测试较为复杂，因此我们就不在此讨论。

关于研究矩阵乘法优化的思考

我们在这里探求单线程的矩阵乘法有没有什么用呢？其实对于绝大部分的人都是用不到的，而且我们研究了许久也连行业最先进水平也没赶上。在实际应用时，绝大部分有矩阵计算需求的人应该都会调用其他的科学计算框架。那么，我们为什么还要在这里研究矩阵乘法的优化呢？

从功利的角度回答，研究矩阵乘法优化的过程中，我们对于如何利用计算机的体系结构特点来进行优化进行了深入的学习和实践，这种经验在其他需要优化的场景中可能是有用的。另外，如果有一天我们需要在一个比较新的计算硬件上用到矩阵乘法，而常用的科学计算库还没有对该硬件进行针对性优化的话，我们或许能够亲自动手优化它。

从非功利的角度回答，just for fun!

https://en.wikipedia.org/wiki/Row-_and_column-major_order↩︎