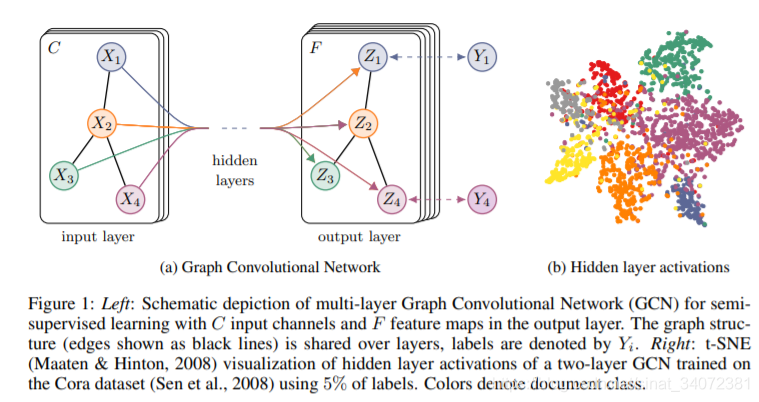
【参考文献】:1. SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
引言
主要解决问题 图半监督分类问题,如引用网络。
一般解决方案及缺点 图半监督学习问题,使用基于图的显示正则化平滑标签信息,如在损失函数中使用图拉普拉斯正则项:
L
=
L
0
+
λ
L
reg
,
with
L
reg
=
∑
i
,
j
A
i
j
∥
f
(
X
i
)
−
f
(
X
j
)
∥
2
=
f
(
X
)
⊤
Δ
f
(
X
)
,
(1)
\mathcal{L}=\mathcal{L}_{0}+\lambda \mathcal{L}_{\text {reg }}, \quad \text { with } \quad \mathcal{L}_{\text {reg }}=\sum_{i, j} A_{i j}\left\|f\left(X_{i}\right)-f\left(X_{j}\right)\right\|^{2}=f(X)^{\top} \Delta f(X), \tag{1}
L=L0+λLreg , with Lreg =i,j∑Aij∥f(Xi)−f(Xj)∥2=f(X)⊤Δf(X),(1)
式中, L 0 \mathcal L_0 L0为仅考虑标注节点的监督损失; f ( ⋅ ) f(\cdot) f(⋅)为可微函数,如神经网络; λ \lambda λ为权重因子; X \bm X X为节点特征向量矩阵; Δ = D − A \Delta=D-A Δ=D−A为无向图未标准化的拉普拉斯矩阵; A A A为邻接矩阵; D D D为节点度矩阵, D i i = ∑ j A i j D_{ii}=\sum_j A_{ij} Dii=∑jAij。
公式1依赖于 “图中相连接的节点可能具有相同标签” 的假设,然而这一假设限制了模型容量,虽然不需要在边中编码节点相似性信息,但边仍可能包含额外的信息。
本文解决方案 使用神经网络模型 f ( X , A ) f(X,A) f(X,A)直接编码图结构,在监督目标 L 0 \mathcal L_0 L0上训练所有带标签的节点,避免在损失函数中引入显式的基于图的正则化。在图邻接矩阵上调整 f ( ⋅ ) f(\cdot) f(⋅),使模型能够从 L 0 \mathcal L_0 L0中分发梯度信息,从而同时学习标注节点和未标注节点的表示。
本文主要贡献
- 第一,提出一种可将神经网络直接应用于图的简单且良好的逐层传播规则,并基于谱图卷积的一阶近似给出推导过程;
- 第二,展示如何以快速、可扩展的方式,将这种形式的图神经网络模型应用于图节点半监督分类;
理论推导
先给出结论,多层图卷积网络(GCN)的逐层传播规则是:
H
(
l
+
1
)
=
σ
(
D
~
−
1
/
2
A
~
D
~
−
1
/
2
H
(
l
)
W
(
l
)
)
,
(2)
H^{(l+1)}=\sigma\left(\tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2} H^{(l)} W^{(l)}\right), \tag{2}
H(l+1)=σ(D~−1/2A~D~−1/2H(l)W(l)),(2)
式中,
- A ~ = A + I N \tilde A=A+I_N A~=A+IN:加入自连接的无向图的邻接矩阵
- I N I_N IN:单位矩阵
- D ~ i i = ∑ j A ~ i j \tilde D_{ii}=\sum_{j}\tilde A_{ij} D~ii=∑jA~ij
- W ( l ) W^{(l)} W(l):第 l l l层参数矩阵
- σ ( ⋅ ) \sigma(\cdot) σ(⋅):激活函数,如ReLU
- H ( l ) ∈ R N × D H^{(l)}\in\R^{N\times D} H(l)∈RN×D:第 l l l层的激活矩阵(特征矩阵), H ( 0 ) = X H^{(0)}=X H(0)=X
这种形式的传播规则可通过图上局部谱滤波器的一阶近似激发。
通俗理解GCN
如果每一层的输入都是邻接矩阵
A
A
A和特征
H
H
H,我们直接做内积(聚合邻接点特征),再乘一个参数矩阵
W
W
W,经激活函数,构建这种简单神经网络是否可以?
f
(
H
(
l
)
,
A
)
=
σ
(
A
H
(
l
)
W
(
l
)
)
f(H^{(l)},A)=\sigma(AH^{(l)}W^{(l)})
f(H(l),A)=σ(AH(l)W(l))
实验证明,这种简单神经网络已经足够强大,但具有局限性;
- A A A对角线元素为0,信息聚合时会丢失自身信息,因此需要加入自连接,即用 A + I A+I A+I替代 A A A;
- A A A没有经过归一化,信息聚合后,分布会发生变化,因此需要做标准化处理让 A A A的行元素之和为1,即可以用 D − 1 / 2 A D − 1 / 2 D^{-1/2}AD^{-1/2} D−1/2AD−1/2替代 A A A;
经以上替换,我们得到层新的传播方式,即公式2。
谱图卷积的一阶近似——GCN
普通形式的拉普拉斯矩阵
L
=
D
−
A
L=D-A
L=D−A,标准化的拉普拉斯矩阵为
L
s
y
s
=
D
−
1
/
2
L
D
−
1
/
2
=
I
−
D
−
1
/
2
A
D
−
1
/
2
=
U
Λ
U
⊤
L^{sys}=D^{-1/2}LD^{-1/2}=I-D^{-1/2}AD^{-1/2}=U\Lambda U^\top
Lsys=D−1/2LD−1/2=I−D−1/2AD−1/2=UΛU⊤
无向图邻接阵 A A A为对称阵,可正交/谱分解, Λ \Lambda Λ为特征值对角阵, U U U为特征向量矩阵。拉普拉斯矩阵的性质:
- 半正定,最小特征值非负;
- 普通形式 L = D − A L=D-A L=D−A,行和为0,最小特征值是0,且对应的特征向量值全为1;
给定信号
x
∈
R
N
x\in\R^N
x∈RN,滤波器
g
θ
=
d
i
a
g
(
θ
)
g_\theta=diag(\theta)
gθ=diag(θ)(由傅里叶空间
θ
∈
R
N
\theta\in\R^N
θ∈RN参数化),谱图卷积定义为
g
θ
⋆
x
=
U
g
θ
U
⊤
x
,
(3)
g_{\theta} \star x=U g_{\theta} U^{\top} x, \tag{3}
gθ⋆x=UgθU⊤x,(3)
其中, U ⊤ x U^\top x U⊤x为 x x x的图傅里叶变换.
谱图卷积由来 给定输入 x \bm x x和卷积核 g \bm g g,则
x ∗ g = F − 1 ( F ( x ) ⊙ F ( g ) ) = U ( U ⊤ x ⊙ U ⊤ g ) \bm x* \bm g=\mathscr F^{-1}(\mathscr F(\bm x)\odot \mathscr F(\bm g))=\bm U(\bm U^\top\bm x\odot\bm U^\top\bm g) x∗g=F−1(F(x)⊙F(g))=U(U⊤x⊙U⊤g)
令 g θ = U T g = d i a g ( U T g ) g_\theta=U^Tg=diag(U^Tg) gθ=UTg=diag(UTg)作为可学习的卷积核,即可推出公式3。
公式4的局限性:
- Λ \Lambda Λ与 U U U相乘的时间复杂度是 O ( N 2 ) O(N^2) O(N2)
- 大型图邻接矩特征分解复杂,计算代价很高
- 基于全局特征学习滤波器,不能应用于不同结构的图
Hammond et al. (2011) 利用特征值对角矩阵的切比雪夫多项式,以
K
K
K阶近似滤波器
g
θ
g_\theta
gθ:
g
θ
′
(
Λ
)
≈
∑
k
=
0
K
θ
k
′
T
k
(
Λ
~
)
,
(4)
g_{\theta^{\prime}}(\Lambda) \approx \sum_{k=0}^{K} \theta_{k}^{\prime} T_{k}(\tilde{\Lambda}), \tag{4}
gθ′(Λ)≈k=0∑Kθk′Tk(Λ~),(4)
式中,各参数意义为
- Λ ~ \tilde \Lambda Λ~为重新调整后的特征值对角矩阵, Λ ~ = 2 Λ / λ max − I N \tilde \Lambda=2\Lambda/\lambda_{\max}-I_N Λ~=2Λ/λmax−IN, λ max \lambda_{\max} λmax为 L L L的最大特征值
- θ ′ ∈ R K \theta'\in\R^K θ′∈RK为切比雪夫系数向量
切比雪夫多项式递归形式为:
T
k
(
x
)
=
2
x
T
k
−
1
(
x
)
−
T
k
−
2
(
x
)
,
T
0
(
x
)
=
1
,
T
1
(
x
)
=
x
T_k(x)=2xT_{k-1}(x)-T_{k-2}(x), \ T_0(x)=1, T_1(x)=x
Tk(x)=2xTk−1(x)−Tk−2(x), T0(x)=1,T1(x)=x,此时,谱图卷积变为
g
θ
′
⋆
x
≈
∑
k
=
0
K
U
θ
k
′
T
k
(
Λ
~
)
U
⊤
x
=
∑
k
=
0
K
θ
k
′
T
k
(
U
Λ
~
U
⊤
)
x
=
∑
k
=
0
K
θ
k
′
T
k
(
L
~
)
x
,
(5)
g_{\theta'} \star x \approx\sum_{k=0}^K U\theta'_kT_k(\tilde \Lambda)U^\top x=\sum_{k=0}^K \theta'_kT_k(U\tilde \Lambda U^\top)x =\sum_{k=0}^K \theta'_kT_k(\tilde L)x, \tag{5}
gθ′⋆x≈k=0∑KUθk′Tk(Λ~)U⊤x=k=0∑Kθk′Tk(UΛ~U⊤)x=k=0∑Kθk′Tk(L~)x,(5)
上式是拉普拉斯中的
K
K
K阶多项式,相当于它仅依赖于离中心点最大
K
K
K步的节点。公式5的时间复杂度与边数量成线性关系。
逐层线性模型
通过堆叠多个公式5形式的卷积层可构造图卷积神经网络。
我们希望模型能够在广度分布节点的图上尽可能减轻局部领域结构的过拟合问题,例如社交网络,引用网络,以及许多真实世界的图数据集。对于固定的计算预算,逐层线性表达允许我们创建更深的模型,这可在许多领域增加模型容量。
我们令
K
=
1
K=1
K=1,
θ
=
θ
0
′
=
−
θ
1
′
\theta=\theta'_0=-\theta'_1
θ=θ0′=−θ1′,且近似
λ
max
≈
2
\lambda_{\max}\approx2
λmax≈2,则公式5简化为
g
θ
′
⋆
x
≈
θ
0
′
x
+
θ
1
′
(
L
−
I
N
)
x
=
θ
0
′
x
−
θ
1
′
D
−
1
/
2
A
D
−
1
/
2
x
⟹
g
θ
⋆
x
≈
θ
(
I
N
+
D
−
1
/
2
A
D
−
1
/
2
)
x
,
(7)
g_{\theta^{\prime}} \star x \approx \theta_{0}^{\prime} x+\theta_{1}^{\prime}\left(L-I_{N}\right) x=\theta_{0}^{\prime} x-\theta_{1}^{\prime} D^{-{1}/{2}} A D^{-{1}/{2}} x \implies g_{\theta} \star x \approx \theta\left(I_{N}+D^{-{1}/{2}} A D^{-{1}/{2}}\right) x, \tag{7}
gθ′⋆x≈θ0′x+θ1′(L−IN)x=θ0′x−θ1′D−1/2AD−1/2x⟹gθ⋆x≈θ(IN+D−1/2AD−1/2)x,(7)
此时,
I
N
+
D
−
1
/
2
A
D
−
1
/
2
I_N+D^{-1/2}AD^{-1/2}
IN+D−1/2AD−1/2的特征值位于区间
[
0
,
2
]
[0,2]
[0,2]。在深度网络中反复应用该算子回造成梯度消失/爆炸,因此引入renormalization trick,令
A
~
=
A
+
I
N
\tilde A=A+I_N
A~=A+IN,则
I
N
+
D
−
1
/
2
A
D
−
1
/
2
=
D
~
−
1
/
2
A
~
D
~
−
1
/
2
I_{N}+D^{-{1}/{2}} A D^{-{1}/{2}}=\tilde{D}^{-{1}/{2}} \tilde{A} \tilde{D}^{-{1}/{2}}
IN+D−1/2AD−1/2=D~−1/2A~D~−1/2
更一般地,对于含有
C
C
C个通道的输入信号,使用
F
F
F个过滤器,有:
Z
=
D
~
−
1
/
2
A
~
D
~
−
1
/
2
X
Θ
,
Z
∈
R
N
×
F
,
X
∈
R
N
×
C
,
Θ
∈
R
C
×
F
,
(8)
Z=\tilde{D}^{-{1}/{2}} \tilde{A} \tilde{D}^{-{1}/{2}} X \Theta, \quad Z \in\R^{N\times F}, X\in\R^{N\times C}, \Theta\in\R^{C\times F}, \tag{8}
Z=D~−1/2A~D~−1/2XΘ,Z∈RN×F,X∈RN×C,Θ∈RC×F,(8)
半监督节点分类
使用公式8构造两层图卷积网络:
Z
=
f
(
X
,
A
)
=
softmax
(
A
^
ReLU
(
A
^
X
W
(
0
)
)
W
(
1
)
)
,
A
^
=
D
~
−
1
/
2
A
~
D
~
−
1
/
2
,
(9)
Z=f(X,A)=\text{softmax}(\hat A\ \text{ReLU}(\hat AXW^{(0)}) W^{(1)}),\quad \hat A=\tilde{D}^{-{1}/{2}} \tilde{A} \tilde{D}^{-{1}/{2}}, \tag{9}
Z=f(X,A)=softmax(A^ ReLU(A^XW(0))W(1)),A^=D~−1/2A~D~−1/2,(9)
无监督多分类任务,在所有有标签的节点上评估损失:
L
=
−
∑
l
∈
Y
L
∑
f
=
1
F
Y
l
f
ln
Z
l
f
,
(10)
\mathcal{L}=-\sum_{l \in \mathcal{Y}_{L}} \sum_{f=1}^{F} Y_{l f} \ln Z_{l f}, \tag{10}
L=−l∈YL∑f=1∑FYlflnZlf,(10)
4 Geometric GCNConv源码
Geometric基于向量形式实现(与加入边权重、去除激活函数的公式2等价):
x
i
(
k
)
=
∑
j
∈
N
(
i
)
∪
i
w
i
,
j
deg
(
i
)
⋅
deg
(
j
)
⏟
1
⋅
(
Θ
(
k
)
⋅
x
j
(
k
−
1
)
)
⏟
2
,
(11)
\pmb x_i^{(k)}= \sum_{j\in\mathcal N(i)\cup {i}}\underbrace{\frac{w_{i,j}}{\sqrt{\text{deg}(i)}\cdot \sqrt{\text{deg}(j)}}}_{1}\cdot \underbrace{\left(\Theta^{(k)}\cdot \pmb x_j^{(k-1)}\right)}_{2}, \tag{11}
xxxi(k)=j∈N(i)∪i∑1
deg(i)⋅deg(j)wi,j⋅2
(Θ(k)⋅xxxj(k−1)),(11)
式中,各参数意义
- deg ( i ) \text{deg}(i) deg(i):节点 i i i的度
- w i , j w_{i,j} wi,j:边 i → j i\to j i→j的权重
- Θ ( k ) \Theta^{(k)} Θ(k):第 k k k层卷积层参数
- x j ( k − 1 ) \pmb x_j^{(k-1)} xxxj(k−1):第 k − 1 k-1 k−1层输出
部分源码:
class GCNConv(MessagePassing):
def __init__(self, in_channels: int, out_channels: int, improved: bool = False, cached: bool = False,
add_self_loops: bool = True, normalize: bool = True, bias: bool = True, **kwargs):
"""
add_self_loops: 是否加入自循环,默认True
normalize:是否加入自循环以及应用对称标准化,默认True
"""
pass
def forward(self, x: Tensor, edge_index: Adj, edge_weight: OptTensor = None) -> Tensor:
"""
x: shape=[num_nodes, num_node_features]
edge_index: shape=[2, num_edhes]
"""
if self.normalize:
if isinstance(edge_index, Tensor):
cache = self._cached_edge_index
if cache is None:
# 对应于公式11的第1部分
edge_index, edge_weight = gcn_norm( # yapf: disable
edge_index, edge_weight, x.size(self.node_dim),
self.improved, self.add_self_loops, dtype=x.dtype)
if self.cached:
self._cached_edge_index = (edge_index, edge_weight)
else:
edge_index, edge_weight = cache[0], cache[1]
elif isinstance(edge_index, SparseTensor):
cache = self._cached_adj_t
if cache is None:
edge_index = gcn_norm( # yapf: disable
edge_index, edge_weight, x.size(self.node_dim),
self.improved, self.add_self_loops, dtype=x.dtype)
if self.cached:
self._cached_adj_t = edge_index
else:
edge_index = cache
# 对应于公式11的第2部分
x = torch.matmul(x, self.weight)
# 对应于公式11中1、2部分相乘,并求和
# propagate_type: (x: Tensor, edge_weight: OptTensor)
out = self.propagate(edge_index, x=x, edge_weight=edge_weight,size=None)
if self.bias is not None:
out += self.bias
return out
def propagate(self, edge_index: Adj, size: Size = None, **kwargs):
"""The initial call to start propagating messages."""
size = self.__check_input__(edge_index, size)
# Run "fused" message and aggregation (if applicable).
if (isinstance(edge_index, SparseTensor) and self.fuse and not self.__explain__):
coll_dict = self.__collect__(self.__fused_user_args__, edge_index, size, kwargs)
msg_aggr_kwargs = self.inspector.distribute(
'message_and_aggregate', coll_dict)
out = self.message_and_aggregate(edge_index, **msg_aggr_kwargs)
update_kwargs = self.inspector.distribute('update', coll_dict)
return self.update(out, **update_kwargs)
# Otherwise, run both functions in separation.
elif isinstance(edge_index, Tensor) or not self.fuse:
# x_j = x.index_select(-2, edge_index[0]), “源节点”features
coll_dict = self.__collect__(self.__user_args__, edge_index, size, kwargs)
msg_kwargs = self.inspector.distribute('message', coll_dict)
# 公式11中1、2部分相乘
out = self.message(**msg_kwargs)
# For `GNNExplainer`, we require a separate message and aggregate
# procedure since this allows us to inject the `edge_mask` into the
# message passing computation scheme.
if self.__explain__:
edge_mask = self.__edge_mask__.sigmoid()
# Some ops add self-loops to `edge_index`. We need to do the
# same for `edge_mask` (but do not train those).
if out.size(self.node_dim) != edge_mask.size(0):
loop = edge_mask.new_ones(size[0])
edge_mask = torch.cat([edge_mask, loop], dim=0)
assert out.size(self.node_dim) == edge_mask.size(0)
out = out * edge_mask.view([-1] + [1] * (out.dim() - 1))
aggr_kwargs = self.inspector.distribute('aggregate', coll_dict)
# 聚合指向相同“目标节点”的特征,对应于公式11求和
out = self.aggregate(out, **aggr_kwargs)
update_kwargs = self.inspector.distribute('update', coll_dict)
return self.update(out, **update_kwargs)
def message(self, x_j: Tensor, edge_weight: OptTensor) -> Tensor:
if edge_weight is None:
return x_j
else:
return edge_weight.view(-1, 1) * x_j
def gcn_norm(edge_index, edge_weight=None, num_nodes=None, improved=False, add_self_loops=True, dtype=None):
fill_value = 2. if improved else 1.
if isinstance(edge_index, SparseTensor):
adj_t = edge_index
if not adj_t.has_value():
adj_t = adj_t.fill_value(1., dtype=dtype)
if add_self_loops:
adj_t = fill_diag(adj_t, fill_value)
deg = sum(adj_t, dim=1)
deg_inv_sqrt = deg.pow_(-0.5)
deg_inv_sqrt.masked_fill_(deg_inv_sqrt == float('inf'), 0.)
adj_t = mul(adj_t, deg_inv_sqrt.view(-1, 1))
adj_t = mul(adj_t, deg_inv_sqrt.view(1, -1))
return adj_t
else:
num_nodes = maybe_num_nodes(edge_index, num_nodes)
if edge_weight is None:
edge_weight = torch.ones(
(edge_index.size(1), ), dtype=dtype, device=edge_index.device)
if add_self_loops:
# 向没有自循环的节点加入自循环,新添加的自循环权重为fill_value
edge_index, tmp_edge_weight = add_remaining_self_loops(
edge_index, edge_weight, fill_value, num_nodes)
assert tmp_edge_weight is not None
edge_weight = tmp_edge_weight
row, col = edge_index[0], edge_index[1]
# 计算目标节点(被指向节点)的度,无向图源节点和目标节点的度相同
deg = scatter_add(edge_weight, col, dim=0, dim_size=num_nodes)
deg_inv_sqrt = deg.pow_(-0.5)
deg_inv_sqrt.masked_fill_(deg_inv_sqrt == float('inf'), 0)
# output shape = [num_edges], [num_edges]
return edge_index, deg_inv_sqrt[row] * edge_weight * deg_inv_sqrt[col]