树结构

树结构有下面的几个缺点

• 空间：占空间较多相对于线性结构
• 创建：构造起来比较麻烦
• 维护：对于平衡树，结构修改（增、删）后又需要平衡

那么，既然这样为什么还要用树结构呢。原因很简单，它的插入和删除操作所使用的时间非常短。红黑树可以在O(log n)的时间内做查找、插入和删除操作。

2-3查找树

直接接受“红黑树”还是有些难以下咽的，红黑树跟2-3查找树有着千丝万缕的联系，因此这里从简单轻松的2-3查找树开始介绍。
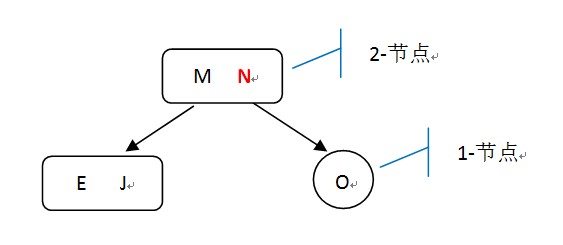
2-3查找树也是一种平衡排序树，2代表一个节点最多有两个值，3代表各节点最多有3个子节点。

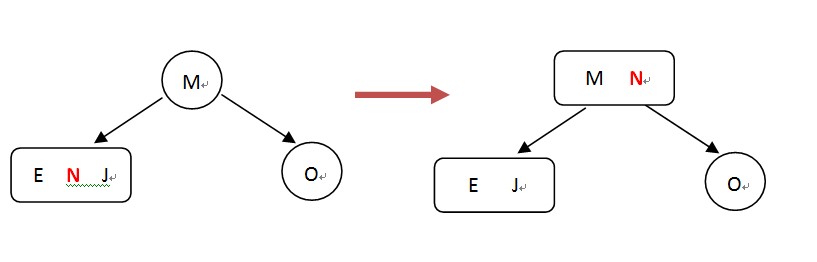
当插入的时候，被插入的位置节点数为1，直接插入；被插入的节点数为2，直接插入变成3节点，这种情况况叫做溢出，选择溢出节点的中位数，上浮到父节点中，父节点如果也溢出，继续溢出处理；当root节点溢出的时候，把中位数构造成新的root，另外两个节点变成它的子节点，这时Tree.height加1，这也是Tree.height唯一变化的方式。

新插入的节点为N

因为2-3查找树不是介绍的重点，因此就