当你陆陆续续学了很多种语言之后,你会发现,虽然各种语言的写法不太一样,但是隐约会觉得各种语言之间的套路差不多。
我们书写的代码是一种高级语言,计算机是不认识的,那么需要有个手段将人类书写下来的高级语言翻译给机器。我们称这个过程为编译。IT领域里面会有个专门的领域叫做【编译原理】,就是解决如何将高级语言转换为计算机可直接识别的语言的问题。
这篇就来讨论java代码的最基本的一些性质,这部分和后面的流程控制共同组合成一般化高级语言的该有的样子。
注释
人们常说代码即文档,意味着你代码写的好,写的规范,看上去就是大白话,而我们从来不会针对大白话再继续进行解释的。
但是,实际上这很难,甚至说这种程度目前基本上是做不到的。我们敲代码事实上涉及到四个角色:
- 写代码的人
- 代码本身
- 计算机
- 阅读代码的人
写代码的人写出代码给阅读代码的人看,【代码即文档】的目标是为了打通写代码和阅读代码的人之间的阅读障碍。代码语言本身是不是简洁,是不是一语中的,和是否能被精确理解有很大关系。很多语言学下来,西班牙语应该是我印象里出错可能性最低的。这个语言内天生制造出了很多变位,句子成分会随着语义语态,主宾单复数,单词阴阳性等等随之改变——给人感觉像什么呢,像是纠错码。在一行语句内很多地方都放置了检验性质的信息,也就是说一个句子本身传递信息的基础上增加了信息的校验能力。
但是,即是人类的语言发展到现在,语言所传达出来的含义也都会出现不精确的特性,这应该是高级语言天生携带的一种属性。反观代码更是这样,况且代码写出来是需要翻译成计算机的,翻译工作是编译器执行,也同样是按照非常死板的方式去翻译。这样就会出现一个矛盾:
高级语言越精简,那么单位容量内的信息量就会高,翻译成本就会高,理解就会费劲,出现偏差的几率就会高。
语言越低级,单位容量内的信息量变低,翻译成本下降,理解是直接的,但是需要去理解的量增大,计算机肯定开心,但是不利于人类去整体把握。
IT领域到处都是平衡,IT的艺术就是平衡的艺术,没有最好,只有平衡。
那么我们就得出这样的结论了:一个计算机语言,不光你要写出优质的阅读性高的代码,也同时需要增加必要的解释给阅读者,除非你这个代码是一次性的,不会存在再次被阅读(包括你自己)的可能性,那么你想怎么写怎么写,怎么快怎么来。
代码需要注释——而不是代码即文档。代码即文档从多个角度上出发都是不完美的,只能说是一种美好的愿景吧。
那么我们接下来看看代码的注释应该怎么写。注释分为两种:
- 单行注释与多行注释
- 文档注释
前者没什么特殊的,就是直白地在代码里对应的位置上写上,只不过因为单行的注释不够写,裂成多行去描述。后者是可以通过javadoc指令将你的注释信息抽取出来变成实实在在的文档,逼格就高了很多。
单行注释与多行注释
原本的代码是这样的
package com.zifang.ex.bust.charpter1.case2;
public class HelloWord {
public static void main(String[] args) {
System.out.println("hello word");
}
}
在这个基础上我们为它增加注释
public class HelloWord {
public static void main(String[] args) {
// 单行注释
System.out.println("hello word");
/* 多行注释,并在一行,看上去就像是单行注释 */
System.out.println("hello word");
System.out/*多行注释甚至可以嵌在分隔符前后*/./**/println("hello word");
System.out.println("hello word");
}
}
可以看到,单行注释就是使用 // ,编译器会将//开始的整行都视为注释。
使用/*开头,/结尾,其之间包裹着的字符串当做注释,不管中间是不是换行。你会发现,这种注解格式是很灵活的,很多地方可以放。但是为了美观一般不会这么做。
文档注释
以/**开头,*/结尾,其中包裹着的字符串会变成文档注释,以下是文档注释的写法
/** 这里是文档注释 */
/**
文档注释同样不关心中间是否有换行
*/
/**
* 但是一般为了美观,文档注释内部换行的话前面会再放个*
* */
public class HelloWord {
public static void main(String[] args) {
// 单行注释
System.out.println("hello word");
/* 多行注释,并在一行,看上去就像是单行注释 */
System.out.println("hello word");
System.out/*多行注释甚至可以嵌在分隔符前后*/./*这里也放*/println("hello word");
System.out.println("hello word");
}
}
我们说多行注释是/*这里是注释/,文档注释是/**这里是注释*/。
如果文档注释里的这里是注释被替换为空字符串,会咋样?是被是识别为多行注释还是文档注释? 答案是后者
如果多行注释里的这里是注释被替换为**,会咋样?还是被识别为文档注释
看来但凡当匹配为文档注释的话就被识别为文档注释
如果文档注释里的这里是注释被替换为/*/,就是说文档注释和多行注释进行嵌套会怎么样?语法报错。
我们要从心底觉得兴奋,并深深地问自己一句:为什么?为什么这个语法不能嵌套?逻辑上的确可以(文档注释内部的其他东西全部识别成字符串不就可以了?),但是就是不行。这就要从java语言的设计出发了,这关系到java编译原理的词法解析和语法树生成的问题。词法解析没问题,该怎么识别怎么识别,问题在于语法树生成,它实际上用的是递归下降式的语法解析,而正因为是使用的递归下降式的解析方式,才会导致上文中出现的问题。你可能不明白这个是什么,后面在说java编译原理的时候会详细描述。
我们接着唠,我们之前说过我们的文档注释是可以生成真正的文档的。JavaApi文档就是这么来的,虽说平时真正开发的时候很少用文档注解,因为觉得没什么必要,但是你可以打开JDK自带的源码,你会发现有些类的代码没多少,注释是真的多。一些小接口的解释相当复杂,你可以从他们的文档中看到作者在写这部分代码时候的心路历程。
文档注释是写给别人看的——意味着我们只需要暴露public,protect的内容,而有必要展示的成分是类,接口,方法,属性,构造器,内部类。当然,javadoc也考虑到事情必有例外,因此javadoc指令是可以增加-private的参数来收集private的信息的。
常用的javadoc标记有
- @author 表达是谁写的
- @version 表达源文件的版本
- @deprecated 表达已经不推荐使用这个了,一般会补充上应该去用哪个类
- @param 表达发布方法入参的说明信息
- @return 表达方法返回值的说明信息
- @see 表达参考,执行参考内容
- @exception 表达抛出的异常的类型
- @throw 表达抛出的异常
注意,这部分标记不是都可以放在同一个成分上的,需要选择。
/**
* 描述:
* <br/> 怎么写文档注释
* @author zifang
* @version 1.0-snapshot
* */
public class HelloWord1 {
/**
* 一个简单的方法
*
* @param a 参数a
* @param b 参数b
* @return 返回
*/
public Object f(String a, String b){
return null;
}
public static void main(String[] args) {
System.out.println("hello world");
}
}
最终可以生成html格式的文档,因此我们的代码内部可以放上一些html标签,例如上文中的<br/>。我总觉得在java里面写html标签是个不对劲的事儿,因此很少干这个事儿。在此不过多去描述javadoc的用法了,参考一下帮助看参数列表,你会发现和java指令是差不多的。maven也有相应的插件帮助你自动完成这种愚蠢的手工任务。
分隔符&标志符&关键字
我们写的代码事实上是需要被编译器理解并且输出成计算机能识别的东西的。类似c或者c++那编译出来的就直接是机器码了,可以直接运行。但是java真正生成的是.class文件,java指令启动了jvm,也就是虚拟机,吃掉你生成的java代码,然后再和真正的物理机打交道。这个时候,你只需要记住,编译器必须理解你写的代码——教会机器理解语言,是不是有点类似于人工智能的样子了?你说这么死板的机器怎么就认识我们的代码呢?这里需要很深的编译原理的知识,这个时候我只告诉你,我们写的代码是要符合规范的,也就是说我们的代码事实上是结构化的,只不过这些结构是由更小的结构单元组合,成为一个大结构。整体而言,还是一个结构化的东西。
那么我们就面临第一个问题,怎么把一个长长的字符串,分解成结构化的东西?或者反过来说,一个东西可以被认定为为是结构化的必要条件是什么。答案是我们需要标记来切开各种小结构。例如我们说一句话:我是帅哥;我们脑子里会什么反应呢?自动把这个句子拆成主语:我,谓语:是,表语:帅哥。然后呢我们就理解了这个意思。你会发现各种语言都是遵循这样的处理方式的。最简单,最实用,计算机也很好处理。代码是死板的,我们需要各种标记切开一个大字符串。这既是分隔符与标志符的所带来的好处。
分隔符与标志符
分隔符分为分号(😉,花括号({}),方括号,圆括号(()),空格,圆点(.)。这几个分隔符各有各的用处,这里简单介绍一下。分号是一个语句的结束,花括号包裹任何表达含义的代码块,方括号用来表达数组,空格可以放在任何地儿,只要不把代码语义结构破坏就可以。圆点表达调用类/对象与其成员。这部分在你去写一段代码之后就会很清楚。但是你需要注意的是,这一切的一切都是设计出来的,你完全可以想出一套崭新的表达方式(即语法),去阐述你的目的。我们常说python很精简,你会发现,它是使用缩进来表达代码的层次结构,这样一来,少了很多分隔符,同样的,代码结构会统一,看上去就很好看。
标志符是用于给程序中变量,类,方法的命名的符号。当然,这里又会有很多规则:
- 标志符可以有字母,数字,下划线,美元符组成,数字不能开头
- 标志符不能是java关键字与保留字
- 标志符不能包含空格,不然相当于是两个标志符
- 标志符只能包含$,不能包含
@,#等特殊字符
虽然你的标志符可以拥有$,_,但是呢,建议不要使用,一方面的确不好看,你的代码写出来是需要像艺术品一样的。不能让这种奇奇怪怪的符号破坏美感。另一方面,标志符里面包含_,在一些特性条件下,会导致bean的驼峰转换变麻烦,本来约定的好好的,你非要放个_进去,驼峰转换完之后没变化,这也就丢失了驼峰转换的意义。针对$,这个会在内部类上,或者编译出来的enum上,或者代理类上,或者lamda表达式产生的类上都会出现。意思是,$ 在一定程度上被赋予了特别的含义。我们能少撞人家的含义就少撞。
关键字
Java关键字是电脑语言里事先定义的,有特别意义的【标识符】。Java的关键字对Java的编译器有特殊的意义。他们用来表示一种数据类型,或者表示程序的结构等。在这里,列出所有的关键字。
| 关键字 | 含义 |
|---|---|
| abstract | 表明类或者成员方法具有抽象属性 |
| assert | 断言,用来进行程序调试 |
| boolean | 基本数据类型之一,声明布尔类型的关键字 |
| break | 提前跳出一个块 |
| byte | 基本数据类型之一,字节类型 |
| case | 用在switch语句之中,表示其中的一个分支 |
| catch | 用在异常处理中,用来捕捉异常 |
| char | 基本数据类型之一,字符类型 |
| class | 声明一个类 |
| const | 保留关键字,没有具体含义 |
| continue | 回到一个块的开始处 |
| default | 1. 用在switch语句中,表明一个默认的分支 |
- Java8 中也作用于声明接口函数的默认实现 |
| do | 用在do-while循环结构中 |
| double | 基本数据类型之一,双精度浮点数类型 |
| else | 用在条件语句中,表明当条件不成立时的分支 |
| enum | 枚举 |
| extends | 表明一个类型是另一个类型的子类型。对于类,可以是另一个类或者抽象类;对于接口,可以是另一个接口 |
| final | 用来说明最终属性,表明一个类不能派生出子类,或者成员方法不能被覆盖,或者成员域的值不能被改变,用来定义常量 |
| finally | 用于处理异常情况,用来声明一个基本肯定会被执行到的语句块 |
| float | 基本数据类型之一,单精度浮点数类型 |
| for | 一种循环结构的引导词 |
| goto | 保留关键字,没有具体含义 |
| if | 条件语句的引导词 |
| implements | 表明一个类实现了给定的接口 |
| import | 表明要访问指定的类或包 |
| instanceof | 用来测试一个对象是否是指定类型的实例对象 |
| int | 基本数据类型之一,整数类型 |
| interface | 接口 |
| long | 基本数据类型之一,长整数类型 |
| native | 用来声明一个方法是由与计算机相关的语言(如C/C++/FORTRAN语言)实现的 |
| new | 用来创建新实例对象 |
| package | 包声明 |
| private | 一种访问控制方式:私用模式 |
| protected | 一种访问控制方式:保护模式 |
| public | 一种访问控制方式:共用模式 |
| return | 从成员方法中返回数据 |
| short | 基本数据类型之一,表达短整数类型 |
| static | 表明具有静态属性 |
| strictfp | 用来声明FP_strict(单精度或双精度浮点数)表达式遵循IEEE 754算术规范 |
| super | 表明当前对象的父类型的引用或者父类型的构造方法 |
| switch | 分支语句结构的引导词 |
| synchronized | 表明一段代码需要同步执行 |
| this | 指向当前实例对象的引用 |
| throw | 抛出一个异常 |
| throws | 声明在当前定义的成员方法中所有需要抛出的异常 |
| transient | 声明不用序列化的成员域 |
| try | 尝试一个可能抛出异常的程序块 |
| void | 声明当前成员方法没有返回值 |
| volatile | 表明两个或者多个变量必须同步地发生变化 |
| while | 用在循环结构中 |
有些关键字在基础开发里会经常使用,少部分是一些高级应用使用场景才会用的到的。还有一部分就更稀少,甚至不是拿来用的。我们把这部分之后长时间内不会涉及到的一些不常见的关键字拿出来,稍稍解释一下。
assert关键字,我们也称为断言,在软件开发中是一种常用的调试方式,很多开发语言中都支持这种机制。断言可以有两种形式:
assert Expression1;
assert Expression1 : Expression2 ;
Expression1 应该总是产生一个布尔值。Expression2 可以是得出一个值的任意表达式,这个值用于生成显示更多调试信息的字符串消息。当Expression1执行为true的时候,正常通过,当Expression1执行为false的时候,系统会报告一个 AssertionError。断言的使用如下面的代码所示:
assert(a > 0); // throws an AssertionError if a <= 0
一般来说,断言用于保证程序最基本、关键的正确性。断言检查通常在开发和测试时开启。为了保证程序的执行效率,在软件发布后断言检查通常是关闭的。要在运行时启用断言,可以在启动 JVM 时使用-enableassertions 或者-ea 标记。 要在运行时选择禁用断言,可以在启动 JVM 时使用-da 或者-disableassertions 标记。要在系统类中启用或禁用断言,可使用-esa 或-dsa 标记。还可以在包的基础上启用或者禁用断言。
native关键字: 通过JNI的调用方式调用c实现,一般的java开发不会去自定义native方法,只会取调用已经有的native方法,常见于数学相关类里。
strictfp关键字: strictfp 的意思是FP-strict,也就是说精确浮点的意思。在Java虚拟机进行浮点运算时,如果没有指定 strictfp 关键字时,Java的编译器以及运行环境在对浮点运算的表达式是采取一种近似于我行我素的行为来完成这些操作,以致于得到的结果往往无法令人满意。而一旦使用了strictfp来声明一个类、接口或者方法时,那么所声明的范围内Java的编译器以及运行环境会完全依照浮点规范IEEE-754来执行。因此如果想让浮点运算更加精确, 而且不会因为不同的硬件平台所执行的结果不一致的话,那就用关键字strictfp。可以将一个类、接口以及方法声明为strictfp,但是不允许对接口中的方法以及构造函数声明strictfp关键字
其他的将会在后续的内容中做详细阐述。
基本数据类型
数据类型是针对变量来说的。对于java这种强类型语言而言,每个变量的类型都是需要预先设定的,因此在编译器借助ide就可以快速发现哪里有问题。声明变量的语法是很简单的:
// 第一种定义变量的方式:类型 变量名
type varName;
// 第二种定义变量的方式:类型 变量名 = 变量值;
type varName = value;
第一种,相当于定义了一个变量varName出来,其类型是type,并赋予varName一个默认的初始值
第二种,相当于定义变量的同时,把value赋值给varName这个变量。
Java支持的数据类型分为两个大类:基本类型,引用类型。
Java语言提供了八种基本类型。六种数字类型(四个整数型,两个浮点型),一种字符类型,还有一种布尔型。分别是:boolean,byte,short,int,long,char,float,double。
引用类型包括,类,接口,数组,还有一个null(特殊的引用,表达什么都不引用)。 引用类型的变量非常类似于C/C++的指针。引用类型指向一个对象,指向对象的变量是引用变量。这些变量在声明时被指定为
一个特定的类型,比如 A、B类等。变量一旦声明后,类型就不能被改变了。对象、数组都是引用数据类型。所有引用类型的默认值都是null。一个引用变量可以用来引用任何与之兼容的类型。
我们画个大表格,这个表格已经足够清晰的表达了我们的基本数据类型的样子。
| 数据类型 | 默认值 | 赋值例子 | 解释 |
|---|---|---|---|
| byte(8位) | 0 | byte b = (byte)1 | -2^7 至 2^7 - 1的整数 byte 数据类型是8位、有符号的,以二进制补码表示的整数 |
| short(16位) | 0 | short b = (short)1 | -2^15 至 2^15 - 1的整数,byte 数据类型是16位、有符号的,以二进制补码表示的整数 |
| int(32位) | 0 | Int b = 1 | -2^31 至 2^31 - 1的整数,byte 数据类型是32位、有符号的,以二进制补码表示的整数 |
| long(64位) | 0L | long l = 1L | -2^63 至 2^63 - 1的整数,byte 数据类型是64位、有符号的,以二进制补码表示的整数 |
| float(32位) | 0.0f | Float f = 1.2f | float 数据类型是单精度、32位、符合IEEE 754标准的浮点数 |
| double(64位) | 0.0 | Double d = 1.2 | double 数据类型是双精度、64 位、符合IEEE 754标准的浮点数 |
| boolean(8位) | false | boolean b = true | boolean数据类型只含有true/false的具体值 |
| char(16位) | \u0000 | char c = ‘吃’ | 范围是:\u0000 -\uffff,使用\\+16位数值表达,java内使用两个单引号来描述 |
整数类型(byte/short/int/long)对于未声明数据类型的整形,其默认类型为int型。
浮点类型(float/double)对于未声明数据类型的浮点型,默认为double型。因此在赋值例子中部分需要强转才可以获得到对应的数值。
整型与进制
整形,表达的是整数。而我们的计算机也只认是0,1。我们的整数分为byte,short,int,long,分别是8,16,32,64位,成2指数次幂扩充的趋势。
什么是进制
为了能够让计算机明白一个整数,我们就要先理解什么是进制。
我们数学上是按照10进1位的方式来描述一个数的,这也和人的生理结构相关。我们有10个手指头。所以可以想象到,古人数数是直接拿着手指头去掰的。还有一种计数呢,是按照手指头的节数数,一根手指头是3节,当三节用完,就让第二根手指的某个节弯曲,这也同样可以数出数字来。这里就有天生的,10进制,3进制的说法了。
那我们就有这样的定义:x进制,指的就是数数的时候,数到x就清零,数值高位进一。即逢x进1。
为什么是二进制
目前计算机是使用二进制的,为什么偏偏是二进制?计算机有多种进制的选择,进制越高,单位长度的信息量就高,那为什么我们不选择高进制来存储数据呢?
我们在选择进制的时候,事实上不光需要考虑信息密度的问题,还需要考虑效率的问题,那什么是效率呢?所谓效率就是在表达单位信息量的前提下,谁消耗的元器件更少,谁的效率就越高。例如使用10进制来表达0-999,这里最大有三位,每个位上需要10个不同的元器件来表达,那么总共需要30个元器件来表达。使用2进制,只需要20个元器件即可,但是20个元器件事实上可以表达0-1023的值。这里就产生了浪费。
假定是x进制,m个数字来表达元器件个数,其值为可表达的数量为 ,我们进行以下变换
,我们进行以下变换

可以看到当 x = e的时候,导数为0,存在最大值。
但是e是个小数,没法表达,3离e接近,反倒是3的信息表达上效率更高。曾经苏联制造过三进制电脑,发现3进制比2进制稳定的多,并且-1,0,1的三种表达在数值上天生携带负数,在逻辑上天生携带0的这种不确定性,是很好地和人的思维相匹配的,相信在人工智能领域会有很高的契合度。但是呢,兜兜转转又回来了,3进制看上去才是王道,但是最终还是2进制统治了人类。这里就有很多因素了,你说二进制是必然吗,也不见得,只能说2进制是符合历史运行规律的。一方面计算机发展过来,2进制实现最简单,材料也便宜。毕竟三态元器件贵嘛。另一方面很多人用2进制的元器件,就成了网络效应,赢者通吃的局面。还有一层就是政治经济因素了,俄罗斯造的这个东西,后来政府不给钱了,怎么搞,搞不下去了嘛。二进制的设计最终称霸了计算机。
十进制转换二进制
我们接着看如何使用二进制来存储数值。
十进制的算法:

那我们推演二进制,看起来只要把底数给替换了就可以了:

我们可以成功计算二进制的数值了!回忆我们的int值,是由4个字节组成,一个字节是8位,那就是32位。那我们算一算32位长度的二进制串最多能表达多少个组成,看做每个位上都有两种可能性,概率上就是全排列组合:K = 2 * 2 * 2..... * 2,总共有32位,那么就有32个2; 即  。
。
这里就有个问题了。负数怎么表达呢?我们知道我们的整数型数据,那都是有正负号的。先哲们思考许久,负数实际上是人的逻辑衍生物,在计算机视角还是只有0,或者1。也就是说我们需要找见一种方式,使得正负数的加减在逻辑上完成自洽。这其中的推演过程还是挺繁杂的,甚至需要结合电子器件的一些行为才可导出结论。在此不做论述,只提供最终结论:
首先假定 :
1 = 00000000 00000000 00000000 00000001
那么-1 就变成这个样子就好,也就是最高位赋值为1:
-1 = 10000000 00000000 00000000 00000001
但是按照这样的方式去直接计算和:1(二进制) +( -1(二进制)) != 0,你会发现这样的计算方式错了,需要修正。因此聪明的科学家们造出【补码】的概念,补码的运算规则如下:
- 正整数的补码 = 正整数
- 负整数的补码 = (~负整数) + 1
a+b相加,不管a,b是正数还是负数,都使用其补码进行加和,超出字长部分直接舍弃。我们举两个例子,假定只能用8位表示:
第一个例子:求两个十进制数的和 35+18。
35(十进制) --- 00100011(二进制) -- 00100011(补码)
18(十进制) --- 00010010(二进制) -- 00010010(补码)
00100011 ---35(十进制)
+
00010010 ---18(十进制)
=
00110101 ---53(十进制)
第二个例子:求两个十进制数的和 35+(-18)。
35(十进制) --00100011(二进制) --00100011(补码)
-18(十进制) --10010010(二进制) --11101110(补码)
00100011
+
11101110
=
100010001
=
00010001(最高位舍弃)
=
17(十进制)
是不是很神奇?背后是有理论的,这部分将在计算机组成原理那里描述其理论。感叹人类的伟大吧!
二进制转换为十进制
上文我们知道了怎么把二进制转换为数值,那反过来呢?我怎么知道一个数值对应的2进制应该是个啥呢?
本质上来说就是找到一个序列{x1,x2…xn}满足以下式子。

我们对这个式子进行变形:

因此我们可以不断进行取余来获得xn的值。假定我们计算60的二进制是什么,可以按照下面的顺序进行计算:
60/2 = 30 余 0
30/2 = 15 余 0
15/2 = 7 余 1
7/2 = 3 余 1
3/2 = 1 余 1
所以十进制数60转为二进制数即为 11100
字符型
我们接下来要解决存储"字"的问题。我们知道,最早搞出计算机的是美国那帮子人,在信息交流上,当然用的就是英语了。英语很简单,使用27个字母组合而成,计算机怎么记住呢?当然还是使用0,1表达。那问题就来了,当计算机看到 0001的时候,它怎么知道这个东西是个’a’,还是’b’呢?没办法,只能给他造一个映射,这个映射全世界都用,是一个标准,没有这个标准,谁都不知道0001代表的是什么。那么我们称这个映射空间叫做"编码集",从字到二进制的映射叫做编码,从二进制到字的映射叫做解码,合称编解码。
ASCII码的诞生
最开始呢,英语嘛,字符没几个,美国最多大概也就用128个符号。没问题,那就整一个7位存储好了,但是呢,一般计算机都是8位成一个byte,行,那就最高位变成0,后面7位当真正的映射。这个编码称为ASCII编码,全称是American Standard Code for Information Interchange,即美国信息互换标准代码。
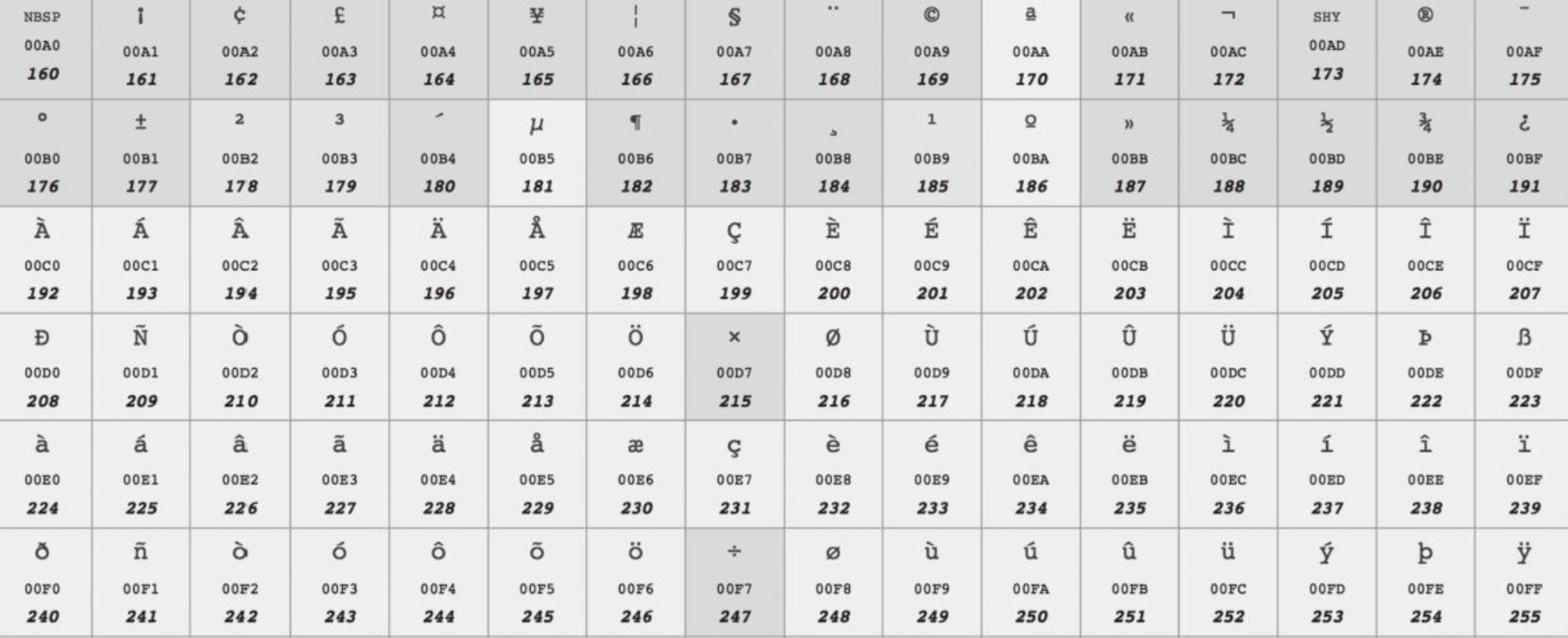
以下是数字32~126的含义;

数字32~126表示的字符都是可打印字符,0~31和127表示一些不可以打印的字符,这些字符一般用于控制目的,这些字符中大部分都是不常用的。下面列出一些我们平时开发过程中经常用到的char。
| 符号 | 解释 |
|---|---|
| \n | 换行 (0x0a) |
| \r | 回车 (0x0d) |
| \f | 换页符(0x0c) |
| \b | 退格 (0x08) |
| \0 | 空字符 (0x0) |
| \s | 空格 (0x20) |
| \t | 制表符 |
| " | 双引号 |
| ’ | 单引号 |
| \ | 反斜杠 |
| \ddd | 八进制字符 (ddd) |
| \uxxxx | 16进制Unicode字符 (xxxx) |
上面的解释不够直观,我们写下这样的代码,这个代码可以帮我们打印出char。从直觉上感知char是个什么东西
public class ASCII {
public static void main(String[] args) {
for(char i = 0; i < 256; i++){
// Integer.toBinaryString(i) 表示使用二进制的方式将i打印出来
System.out.println((int)i+"->"+Integer.toBinaryString(i)+"->"+i);
}
}
}
得到的结果长这个样子:
0->0->
1->1->
2->10->
// 这里略去,
29->11101->
30->11110->
31->11111->
32->100000->
33->100001->!
34->100010->"
35->100011->#
// 后面略去
最右边没有打印出来的,证实了我们之前说的,32号以下都是不能打印的字符。
上面的列表中最常用的是换行与回车。在计算机还没有出现之前,有一种叫做电传打字机的东西,每秒钟可以打10个字符。但是它有一个问题,就是打完一行换行的时候,要用去0.2秒,正好可以打两个字符。要是在这0.2秒里面,又有新的字符传过来,那么这个字符将丢失。于是,研制人员想了个办法解决这个问题,就是在每行后面加两个表示结束的字符。一个叫做"回车",告诉打字机把打印头定位在左边界;另一个叫做"换行",告诉打字机把纸向下移一行。这就是"换行"和"回车"的来历。后来,计算机发明了,这两个概念也就被般到了计算机上。那时,存储器很贵,一些科学家认为在每行结尾加两个字符太浪费了,加一个就可以。于是,就出现了分歧。
- Unix系统里,每行结尾只有”<换行>”,即”\n”;
- Windows系统里面,每行结尾是”<回车><换行>”,即”\r\n”;
- Mac系统里,每行结尾是”<回车>”,即”\r”。
一个直接后果是,Unix/Mac系统下的文件在Windows里打开的话,所有文字会变成一行;而Windows里的文件在Unix/Mac下打开的话,在每行的结尾可能会多出一个^M符号。
ASCII码的扩展
到后来,计算机火了,各个地区都要用计算机了,ASCII码明显不够了,就我们中文里面的汉字数量,那叫一个大。于是,各个国家的各种计算机厂商就发明了各种各种的编码方式以表示自己国家的字符,为了保持与ASCII码的兼容性,一般都是将最高位设置为1。也就是说,当最高位为0时,表示ASCII码,当为1时就是各个国家自己的字符。在这些扩展的编码中,在西欧国家中流行的是ISO 8859-1和Windows-1252,在中国是GB2312、GBK、GB18030和Big5
- ISO 8859-1(Latin-1)
ISO 8859-1字符集使用一个字节表示一个字符,其中0~127与ASCII一样,128~255规定了不同的含义。在128~255中,128~159表示一些控制字符,这些字符也不常用。160~255表示一些西欧字符。如下图所示:
- Windows-1252
ISO 8859-1虽然号称是标准,用于西欧国家,但它连欧元(€)这个符号都没有,因为欧元比较晚,而标准比较早。实际中使用更为广泛的是Windows-1252 编码,这个编码与ISO8859-1基本是一样的,区别只在于数字128~159。Windows-1252使用其中的一些数字表示可打印字符。
这个编码中加入了欧元符号以及一些其他常用的字符。基本上可以认为,ISO 8859-1已被Windows-1252取代,在很多应用程序中,即使文件声明它采用的是ISO 8859-1编码,解析的时候依然被当作Windows-1252编码。
HTML5甚至明确规定,如果文件声明的是ISO 8859-1编码,它应该被看作Win-dows-1252编码。为什么要这样呢?因为大部分人搞不清楚ISO 8859-1和Windows-1252的区别,当他说ISO 8859-1的时候,其实他指的是Windows-1252,所以标准干脆就这么强制规定了。
- GB2312
美国和西欧字符用一个字节就够了,但中文显然是不够的。中文第一个标准是GB2312。GB2312标准主要针对的是简体中文常见字符,包括约7000个汉字和一些罕用词和繁体字。GB2312固定使用两个字节表示汉字,在这两个字节中,最高位都是1,如果是0,就认为是ASCII字符。在这两个字节中,其中高位字节范围是0xA1~0xF7,低位字节范围是0xA1~0xFE。 - GBK
GBK建立在GB2312的基础上,向下兼容GB2312,也就是说,GB2312编码的字符和二进制表示,在GBK编码里是完全一样的。GBK增加了14000多个汉字,共计约21000个汉字,其中包括繁体字。GBK同样使用固定的两个字节表示,其中高位字节范围是0x81~0xFE,低位字节范围是0x40~0x7E和0x80~0xFE。需要注意的是,低位字节是从0x40(也就是64)开始的,也就是说,低位字节的最高位可能为0。那怎么知道它是汉字的一部分,还是一个ASCII字符呢?其实很简单,因为汉字是用固定两个字节表示的,在解析二进制流的时候,如果第一个字节的最高位为1,那么就将下一个字节读进来一起解析为一个汉字,而不用考虑它的最高位,解析完后,跳到第三个字节继续解析。 - GB18030
GB18030向下兼容GBK,增加了55000多个字符,共76000多个字符,包括了很多少数民族字符,以及中日韩统一字符。用两个字节已经表示不了GB18030中的所有字符,GB18030使用变长编码,有的字符是两个字节,有的是四个字节。在两字节编码中,字节表示范围与GBK一样。在四字节编码中,第一个字节的值为0x81~0xFE,第二个字节的值为0x30~0x39,第三个字节的值为0x81~0xFE,第四个字节的值为0x30~0x39。
解析二进制时,如何知道是两个字节还是4个字节表示一个字符呢?看第二个字节的范围,如果是0x30~0x39就是4个字节表示,因为两个字节编码中第二个字节都比这个大 - Big5
Big5是针对繁体中文的,广泛地用在我国台湾地区和我国香港特别行政区等地。Big5包括13000多个繁体字,和GB2312类似,一个字符同样固定使用两个字节表示。在这两个字节中,高位字节范围是0x81~0xFE,低位字节范围是0x40~0x7E和0xA1~0xFE。
Unicode的诞生
从上面你会发现,编码集怎么这么多,一多就不想学了。那有人就想了,世界上所有的字符能不能统一编码呢?
可以,Unicode就是为了实现这个目标而诞生了。Unicode做了一件事,就是给世界上所有字符都分配了一个唯一的数字编号,这个编号范围从0x000000~0x10FFFF,包括110多万。但大部分常用字符都在0x0000~0xFFFF之间,即65536个数字之内。每个字符都有一个Unicode编号,这个编号一般写成十六进制,在前面加U+。大部分中文的编号范围为U+4E00~U+9FFF。
注意:Unicode并没有规定这个编号怎么对应到二进制表示,这是与上面介绍的其他编码不同的,其他编码都既规定了能表示哪些字符,又规定了每个字符对应的二进制是什么,而Unicode本身只规定了每个字符的数字编号是多少。
Unicode给世界上所有字符都规定了一个统一的编号,编号范围达到110多万,但大部分字符都在65536以内。
Unicode本身没有规定怎么把这个编号对应到二进制形式。因此这里必须存在将编号映射为二进制的转换逻辑,这也是UTF-32/UTF-16/UTF-8存在的必要性。事实上按理说 Unicode 已经给世界范围内的所有字符定义了代码点,无论是什么字符,使用4个字节都能表示出来,但是为什么会有这三种编码的区分呢?
这是因为使用者发现,对于ASCII码范围内的字符,本来1个字节就能正确表示,现在居然要4个字节表示。为了解决这种空间浪费问题,就出现了一类变长的通用转换格式,即UTF(Universal Transformation Format),常见的UTF格式有:UTF-8,UTF-16 以及 UTF-32。
UTF-32
UTF-32是最简单的,就是字符编号的整数二进制形式,4个字节。这里有个细节,就是字节的排列顺序,如果第一个字节是整数二进制中的最高位,最后一个字节是整数二进制中的最低位,那这种字节序就叫“大端”(Big Endian,BE),否则,就叫“小端”(Little Endian,LE)。对应的编码方式分别是UTF-32BE和UTF-32LE。可以看出,每个字符都用4个字节表示,非常浪费空间,实际采用的也比较少。
UTF-16
UTF-16使用变长字节表示:
- 对于编号在U+0000~U+FFFF的字符(常用字符集),直接用两个字节表示。需要说明的是,U+D800~U+DBFF的编号其实是没有定义的。
- 字符值在U+10000~U+10FFFF的字符(也叫做增补字符集),需要用4个字节表示。前两个字节叫高代理项,范围是U+D800~U+DBFF;后两个字节叫低代理项,范围是U+DC00~U+DFFF。区分是两个字节还是4个字节表示一个字符就看前两个字节的编号范围,如果是U+D800~U+DBFF,就是4个字节,否则就是两个字节。
UTF-16也有和UTF-32一样的字节序问题,如果高位存放在前面就叫大端(BE),编码就叫UTF-16BE,否则就叫小端,编码就叫UTF-16LE。UTF-16常用于系统内部编码,UTF-16比UTF-32节省了很多空间,但是任何一个字符都至少需要两个字节表示,对于美国和西欧国家而言,还是很浪费的。
UTF-8
UTF-8使用变长字节表示,每个字符使用的字节个数与其Unicode编号的大小有关,编号小的使用的字节就少,编号大的使用的字节就多,使用的字节个数为1~4不等。各个Unicode编号范围对应的二进制格式下表所示:
| Unicode/UCS-4(十六进制) | 字节数 | **UTF-8编码格式(二进制) |
|---|---|---|
| 000000-00007F | 1 | 0xxxxxxx |
| 000080-0007FF | 2 | 110xxxxx 10xxxxxx |
| 000800-00FFFF | 3 | 1110xxxx 10xxxxxx 10xxxxxx |
| 010000-10FFFF | 4 | 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx |
x表示可以用的二进制位,而每个字节开头的1或0是固定的。
小于128的,编码与ASCII码一样,最高位为0。其他编号的第一个字节有特殊含义,最高位有几个连续的1就表示用几个字节表示,而其他字节都以10开头。 对于一个Unicode编号,具体怎么编码呢?首先将其看作整数,转化为二进制形式(去掉高位的0),然后将二进制位从右向左依次填入对应的二进制格式x中,填完后,如果对应的二进制格式还有没填的x,则设为0。
只看上面这种对应关系,可能还不太清楚是怎样表示,接下来可以举一个例子试一下,比如一个常用的简体中文字:“好”,查询它的Unicode代码点是 \u597D,对照上面的表格发现在 000800-00FFFF 这个范围,应该采用3个字节的表现形式。
- 先把这个数值翻译成二进制为 0101100101111101
- 按照3个字节的形式分成3组,0101、100101 和 111101
- 将上面这些内容天填充到xxx这样的空位中
- 得到 11100101 10100101 10111101,表示成十六进制就是 0xE5A5BD,这个值就是“好”这个字的编码
根据 UTF-8 的编码规则,任何一个 byte 漏传,多传,传错只影响当前字符,前后字符都不受影响,而 Unicode 如果从一个字的中间截断会导致接下来所有的字符解析都是错的,这使得UTF-8编码的数据在不够可靠的网络传输中是有利的。
UTF-8 兼容ASCII,并且是字节顺序无关的。它的字节顺序在所有系统中都是一样的,因此它实际上并不需要BOM,不过在文件开头常常保存 0xEFBBBF 三个字节来表明文件编码是UTF-8。
UTF-8是一种变长编码,无法从直接从Unicode字符直接判断出UTF-8文本的字节数。除了ASCII字符集内的字符,其他情况实际上都增加了固定的头数据,占用了无效空间。
乱码问题
字符串在java中统一用unicode表示( 即utf-16 LE) ,如果源码文件是GBK编码, 操作系统(windows)默认的环境编码为GBK,那么编译时, JVM将 按照GBK编码将字节数组解析成字符,然后将字符转换为unicode格式的字节数组,作为内部存储。
当打印这个字符串时,JVM 根据操作系统本地的语言环境,将unicode转换为GBK,然后操作系统将GBK格式的内容显示出来。
当源码文件是UTF-8, 我们需要通知编译器源码的格式,javac -encoding utf-8 … , 编译时,JVM按照utf-8 解析成字符,然后转换为unicode格式的字节数组, 那么不论源码文件是什么格式,同样的字符串,最后得到的unicode字节数组是完全一致的,显示的时候,也是转成GBK来显示(跟OS环境有关)
一串已经解码后的字符,我们也可以选用任意类型的编码方式重新转换成一串二进制数,这个过程就是编码。无论使用哪一种编码方式进行编码,最终都是产生计算机可识别的二进制数,但如果编码规范的字库表不包含目标字符,则无法在字符集中找到对应的二进制数。这将导致不可逆的乱码。例如:ISO-8859-1的字库表中不包含中文,因此哪怕将中文字符使用ISO-8859-1进行编码,再使用ISO-8859-1进行解码,也无法显示出正确的中文字符。
本质上都是由于字符串原本的编码格式 与 读取时解析用的编码格式 不一致导致的。
/**
* windows下
*/
public static void main(String a[]) throws UnsupportedEncodingException{
String s = "你好哦!";
System.out.println( new String(s.getBytes(),"UTF-8"));
//因为getBytes()默认使用GBK编码, 而解析时使用UTF-8编码,肯定出错。
}
其中 getBytes() 是将unicode 转换为操作系统默认的格式的字节数组,即"你好哦"的 GBK格式。
new String (bytes, Charset) 中的charset 是指定读取 bytes 的方式,这里指定为UTF-8,即把bytes的内容当做UTF-8 格式对待。
如下两种方式都会有正确的结果,因为他们的源内容编码和解析用的编码是一致的。
System.out.println( new String(s.getBytes(),"GBK"));
System.out.println( new String(s.getBytes("UTF-8"),"UTF-8"));
浮点型
| 符号位 | 指数位 | 尾数位 | 数值 | 含义 |
|---|---|---|---|---|
| 0 | 全为0 | 全为0 | +0 | 正数0 |
| 1 | 全为0 | 全为0 | -0 | 负数0 |
| 0 | 全为0 | 任意取值f | 0. f ∗ 2 − 126 0.f _ 2^{-126}0._f*∗2−126 | 非标准值,尾数前改为0,提高了精度 |
| 1 | 全为0 | 任意取值f | − 0. f ∗ 2 − 126 -0.f _ 2^{-126}−0._f*∗2−126 | 非标准值,尾数前改为0,提高了精度 |
| 0 | 全为1 | 全为0 | +Infinity | 正无穷大 |
| 1 | 全为1 | 全为0 | -Infinity | 负无穷大 |
| 0/1 | 全为1 | 不全为0 | NaN | 非数字,用来表示一些特殊情况 |
我们知道,一个int是32位,取值范围是 [-2147483648, 2147483647] ,一共是4,294,967,296种可能。整形完全抛弃了小数点。那如果换成float呢?我们知道float也是32位,从信息量角度上说,32位的0,1组合最多也就4,294,967,296种可能。也就是说,float也就最多表达4,294,967,296种的可能值。那我们可以怎么做呢?本质上来说,float的表示是在做映射的事儿。还是以int来举例,int的每种可能性都映射成为一个确定的整数,整数间最小间距是1。float的目标是小数点也可以表示出来,那怎么办?我们如果使用间距很小的值作为最终映射出来的集合的最小间距,那么映射之后最终的值域范围就很小。看来选定一个好的映射函数是个核心问题。
浮点数的二进制表示
我们先考虑float的计算特性,就是我们期望float计算的一些特征
1)0.0000001+0.0000001 = 0.0000002,这个小数的结果应该尽可能精确。
2)111111111.0000001+111111111.0000001 = 22222222.0000002,这个小数的结果好像可以直接省略0.000002,就是说,两个大的小数计算结果可以忽略一些小的值,差了点没什么特别大的损失。
那我们就有招了,我们的映射函数转换为幂指数转换e^x ,x取值负数,变动会很小,x取正整数,变动会很大。用概念上的示意图表达,可以长这样。
//int
[ * * * 0 * * * ]
//float
[ * * * * * * * * * * * 0 * * * * * * * * * * *]
可以看到,int和float的可能性(点数)是一致的,但是映射出来的数值范围可以很大。
常用科学计数法是将所有的数字转换成 的形式,其中a的范围是1到9共9个整数,b是小数点后的所有数字,c是10的指数。而计算机中存储的都是二进制数据,所以float存储的数字都要先转化成
的形式,其中a的范围是1到9共9个整数,b是小数点后的所有数字,c是10的指数。而计算机中存储的都是二进制数据,所以float存储的数字都要先转化成 ,由于二进制中最大的数字就是1,所以表示法可以写成
,由于二进制中最大的数字就是1,所以表示法可以写成 的形式,float要想存储小数就只需要存储(±),b和c就可以了。
的形式,float要想存储小数就只需要存储(±),b和c就可以了。
float的存储正是将4字节32位划分为了3部分来分别存储正负号,小数部分和指数部分的。用公式来表达就是:

- Sign(1位):用来表示浮点数是正数还是负数,0表示正数,1表示负数。
- Exponent(8位):指数部分。即上文提到数字c,但是这里不是直接存储c,为了同时表示正负指数以及他们的大小顺序,这里实际存储的是c+127。
- Mantissa(23位):尾数部分。也就是上文中提到的数字b。
以数字6.5为例,看一下这个数字是怎么存储在float变量中的:
先来看整数部分,模2求余可以得到二进制表示为110。再来看小数部分,乘2取整可以得到二进制表示为.1。拼接在一起得到110.1然后写成类似于科学计数法的样子,得到 。
。
从上面的公式中可以知道符号为正,尾数是101,指数是2。
符号为正,那么第一位填0,指数是2,加上偏移量127等于129,二进制表示为10000001,填到2-9位,剩下的尾数101填到尾数位上即可。明白了上面的原理就可求float类型的范围了,找到所能表示的最大值,然后将符号为置为1变成负数就是最小值,要想表示的值最大肯定是尾数最大并且指数最大,那么可以得到尾数为 0.1111111 11111111 11111111,指数为 11111111,但是指数全为1时有其特殊用途,所以指数最大为 11111110,指数减去127得到127,所以最大的数字就是 ,这个值为 340282346638528859811704183484516925440,通常表示成 3.4028235E38,那么float的范围就出来了:
,这个值为 340282346638528859811704183484516925440,通常表示成 3.4028235E38,那么float的范围就出来了:
[-3.4028235E38, 3.4028235E38]
浮点数计算不精确问题
一般java里面做浮点数运算,如果是需要非常精确的场合,就使用BigDecimal类即可。虽然慢一点,但是不失真。这点也经常在金融体系内使用。如果你把一个很大的float数和很小的float数相加,大数记不了那么小的数,就直接抹掉了,如果你进行这样的计算 大float + 小float + 小float … 很多很多次,最后你发现可能还是等于大float。可以看到,浮点数的存储事实上是不精确的。如下例子:
public class FloatPrecision {
public static void main(String[] args) {
float sum = 0.0f;
for (int i = 0; i < 20000000; i++) {
float x = 1.0f; sum += x;
}
System.out.println("sum is " + sum); }
}
对应的结果是这样的:
sum is 1.6777216E7
那我们反过来说,如果我就希望大数+小数+小数…计算累加,而且最后的值也要精确(当然,这不可能),这里的目标是足够精确,那要怎么办呢?
面对这个问题,聪明的计算机科学家们也想出了具体的解决办法。他们发明了一种叫作Kahan Summation的算法来解决这个问题。算法的对应代码我也放在文稿中了。从中你可以看到,同样是 2000 万个 1.0f 相加,用这种算法我们得到了准确的 2000 万的结果。
public class KahanSummation {
public static void main(String[] args) {
float sum = 0.0f;
float c = 0.0f;
for (int i = 0; i < 20000000; i++) {
float x = 1.0f;
float y = x - c;
float t = sum + y;
c = (t-sum)-y;
sum = t;
}
System.out.println("sum is " + sum);
}
}
输出的结果是:
sum is 2.0E7
这个算法的原理其实并不复杂,就是在每次的计算过程中,都用一次减法,把当前加法计算中损失的精度记录下来,然后在后面的循环中,把这个精度损失放在要加的小数上,再做一次运算。
布尔型
我们程序世界需要判断对或者不对,而本质上判断对或者不对的信息量很少,一个bit就可以来表达。这么说来,是不是意味着也可以使用0,1来表达对和错呢?
public class Foo {
public static void main(String[] args) {
int eated = 0;
if (0 == eated) {
System.out.println("真吃了");
}
}
看上去问题不大,走的通。但是一想,0,1毕竟只是数字,而对与错是我们人类赋予给0,1的概念。如果不同的人赋予的概念不一样,那不是乱了套了嘛?因此,java定义了true与false来表达"对"或者"错"。那么上面的代码就将会改成:
public class Foo {
public static void main(String[] args) {
boolean eated = true;
if (true != eated) {
System.out.println("没吃");
}
}
这样就很美观,给人的阅读体验就很好。
那我们深入一层,我们虚拟机去执行这个java代码的时候,内存里到底是怎么存的?编译后的.class文件内,都将使用int值来存储布尔值。严谨一点的说法是:java虚拟机规范中,将boolean类型映射为int类型。
即,"true"映射为1,"false"映射为0;看下面的代码:
public class Foo {
public static void main(String[] args) {
boolean eated = 2; // 直接编译的话javac会报错
if (eated)
System.out.println("吃了");
}
if (true == eated) {
System.out.println("真吃了");
}
}
这样的代码直接编译是报错的,java编译器将会阻止编译通过。但是我们会有手段直接将字节码改写,逻辑上就会变成上面的代码的含义。如果你跑过这段代码,你会发现,问虚拟机“吃过饭没”,它会回答“吃了”,而问虚拟机“真(==)吃过饭没”,虚拟机则不会回答“真吃了”。
字节码内部已经没有布尔的痕迹了,对于eated这个局部变量而言,已经是int值。因此我们可以在字节码上动手脚,jvm不限制局部变量值是什么,那是java语言规范规定的,编译器+java语言规范可以保证eated的值肯定是0,或者1。
那么 eated = 2 会导致if判定为真(底层使用ifeq指令,判定操作数栈上数值为0时跳转),而是否==true则判定为假(第二个if语句会被翻译为if_icmpne指令,即操作数栈上两个数值不相同时跳转)。
我们再深入一层,假如将上面的代码改成这样:
public class Foo {
private static eated;
public static void main(String[] args) {
eated = true; // 使用工具改写字节码,变成2或者3
if (eated)
System.out.println("吃了");
}
if (true == eated) {
System.out.println("真吃了");
}
}
尝试将eated更改为2,或者3,会变成什么样呢?这个时候我们就需要引入一个新的底层机制:
在将 boolean,byte,char,short 的值存入字段时,Java 虚拟机会进行掩码操作。
在读取时,Java 虚拟机则会将其扩展为 int 类型。
什么意思呢,如果我们将eated = 2,2的二进制码是000000000000010,而boolean只需要一个byte,而且只需要一位码位,则只取最后一位,得到0的值(一个字节),3则可以获得1的值(一个字节存储)。当读取的时候,扩展为int(4个字节)进行计算。
说了这么多,没啥意思,工作上也用不到。但是我还是坚定一个想法,你需要有思考的能力,去探究本质,本质化的知识才可以被推演,被迁移。方可立于不败之地。
基本类型的类型转换
我们手上有8中基础类型,可以简单分为三种:
- 数值类型,包含整数或者浮点数
- char类型
- 布尔类型
我们这里说的基本类型转换只限于数值类型与char类型,布尔准确的说不算数值,算逻辑,因此代码需要转换的场景也是很少的。
而数据类型转换法则可以简单归结为两条线路:
- 数值型数据之间的转换
- 数值型数据与char类型之间的转换
数值型数据之间的转换
我们先看第一条:数值型数据之间的转换
从数值域上说,类型的排布是这样的:byte ->short->int->long->float->double
那么总结下来会有这样的法则:
TargetType t = sourceTypeValue;
sourceTypeValue指的是参数的赋值的左边项,就是被赋值的那个域,右边是某个类型的值。
Case1 : 当TargetType = sourceType是一样的,那就不需要转换,直接用就好了。
Case2 : 当TargetType值域范围 > sourceType,也不需要改什么,因为小的值自动就会变成大的值的类型,这个是jvm做的自动转换。
世界上哪有自动不自动的事儿,都是因为被抽象被隐藏了细节的原因。如果写出这样的代码,实际上字节码编译出来自动会插入转换的指令,因此高级语言开发者就可以不需要管这种事儿。
Case3 : 当TargetType值域范围 < sourceType的值域范围,意味着大的数值放到小的数值里存储,可能会丢失值。开发者必须要告诉计算机要不要进行转换。正因为如此我们的语句就需要进行更改了:
TargetType t = (TargetType)sourceTypeValue;
这里的()所干的事儿就是强制转换,目的就是无视超出值域的部分。例如浮点数转换为整形,小数点后面的就要舍弃。
但是呢,这里还有一些值得玩味的例子:
例子1:
int a = 233;
byte b = (byte)a;
b的值是-23。为什么结果是-23?需要从最根本的二进制存储考虑。
233的二进制表示为:24位0 + 11101001,byte型只有8位,于是从高位开始舍弃,截断后剩下:11101001,由于二进制最高位1表示负数,0表示正数,其相应的负数为-23。
例子2:
byte b = (byte)-15;
int i = b;
i 的值是-15,看来转换还是很智能的,可以保留正负号。
上面两个例子涉及到比较特别的转换规则:
- 如果最初的数值类型是有符号的,那么就执行符号扩展;如果是char类型,那么不管它要被转换成什么类型,都执行零扩展。
- 如果目标类型的长度小于源类型的长度,则直接截取目标类型的长度。例如将int型转换成byte型,直接截取int型的右边8位。
这里提到了一个新词儿——扩展,专业点说也就是符号扩展,那么什么是符号扩展(Sign Extension)呢?
符号扩展用于在数值类型转换时扩展二进制位的长度,以保证转换后的数值和原数值的符号(正或负)和大小相同,一般用于较窄的类型(如byte)向较宽的类型(如int)转换。扩展二进制位长度指的是,在原数值的二进制位左边补齐若干个符号位(0表示正,1表示负)。
使用上面的举子来说,如果用6个bit表示十进制数10,二进制码为"00 1010",如果将它进行符号扩展为16bits长度,结果是"0000 0000 0000 1010",即在左边补上10个0(因为10是正数,符号为0),符号扩展前后数值的大小和符号都保持不变;如果用10bits表示十进制数-15,使用“2的补码”编码后,二进制码为"11 1111 0001",如果将它进行符号扩展为16bits,结果是"1111 1111 1111 0001",即在左边补上6个1(因为-15是负数,符号为1),符号扩展前后数值的大小和符号都保持不变。
char类型与数值类型之间的转换
我们来看第二条:char类型与数值类型之间的转换
我们知道char从存储量来说,和short一样都是2个字节,16位。
char c1 = (byte)78;
char c2 = (short)78;
char c3 = 78;
char c33 = 0x7fffffff;// 编译错误
char c4 = 78L;// 编译错误
char c11 = (byte)-78; // 编译错误
char c21 = (short)-78; // 编译错误
char c31 = -78; // 编译错误
从这里可以看出规律:
- 使用小的直接量赋值给char,只要不是明确的long类型及以上,可以直接赋值。
- 使用大的直接量,是不能直接给char赋值的,这个极限是2*16
- 负数不可以赋值给char
接下来我们来个有难度的:
例子3:
int n = (int)(char)(byte)-1
按照我们之前描述的规则,我们是这么分析的:
1. int(32位) -> byte(8位)
-1是int型的字面量,根据“2的补码”编码规则,编码结果为0xffffffff,即32位全部置1.转换成byte类型时,直接截取最后8位,所以byte结果为0xff,对应的十进制值是-1.
2. byte(8位)-> char(16位)
由于byte是有符号类型,所以在转换成char型(16位)时需要进行符号扩展,即在0xff左边连续补上8个1(1是0xff的符号位),结果是0xffff。由于char是无符号类型,所以0xffff表示的十进制数是65535。
3. char(16位)-> int(32位)
由于char是无符号类型,转换成int型时进行零扩展,即在0xffff左边连续补上16个0,结果是0x0000ffff,对应的十进制数是65535。
直接量
直接量是指在程序中通过源代码直接给出的值,例如在int a = 5; 代码中,为变量 a 所分配的初始值 5 就是一个直接量。
而所有的8种变量的写法规则如下:
- byte,short
- 都需要使用对应的类型进行强转,例如 (byte)12,(short)3
- int 类型
- 二进制,需要以 0B 或 0b 开头
- 十进制,默认
- 八进制,需要以 0 开头
- 十六进制 ,需要以 0x 或 0X 开头
- long 类型
- 在数值后添加 l 或 L 后就变成了 long 类型的直接量,例如15L
- float 类型的直接量
- 在浮点数后添加 f 或 F 就变成了 float 类型的直接量,例如3.14F
- 也可以是科学计数法形式,例如3.14E8f
- double 类型的直接量
- 默认带小数的数值都为double,例如 3.14
- 明确在带小数的数值之后增加D,例如3.14D
- 也可以是科学计数法形式,例如3.14E8D
- boolean 类型的直接量
- 直接量只有 true 和 false。
- char 类型的直接量
- 单引号括起来的字符,例如‘a’
- 转义字符,例如‘\t’
- Unicode 值,例如‘\u0065’
为了提高可读性,java允许直接量的数字间使用“_”,例如232_23_233,33.33_33D
运算符
算数运算符
算术运算符主要用于进行基本的算术运算,+ - * / % ++ --,加减乘数,取余,都很好理解。但是当操作数是字符串时,加(+)运算符用来合并两个字符串。
当加(+)运算符的一边是字符串,另一边是数值时,机器将自动将数值转换为字符串,并连接为一个字符串。
String a ="aa";
int c = 555;
String b = a+"bbb"+c;
System.out.println(b);
输出为:aabbb555
其中需要详细说明的是++和–,我很讨厌这俩符号,甚至觉得就没有必要制造这两种符号。
int i = 0;
int j = i++ //将j赋值i,然后计算 i= i+1
int z = ++i // 先计算 i= i+1,然后将i的值赋值给j
从上面的语句可以看到,会精简一点,但是丢失了阅读体验,在脑子里面需要计算一把,虽然有点面向过程编码的样子,但是是两步并做一步的方式。然后呢,面试题经常会出现 ----i+±-++考人,这有意思吗?没意思,纯粹是在玩弄人的情感。go语言已经删除了这种写法,乖乖地去写人类容易理解的高级语句就行。虽然字节码针对这个自加也有对应的指令,而且这个指令是直接操作方法列表里面的值——这也导致了打破字节码执行的规律(基本上都是操作数栈,方法列表,数据拷贝来拷贝去的过程)
赋值运算符
最核心的就是 =,除此之外还有特殊的赋值运算,如下条目:
● +=:对于a+=b,即对应于a=a+b。
● -=:对于a-=b,即对应于a=a-b。
● =:对于a=b,即对应于a=a*b。
● /=:对于a/=b,即对应于a=a/b。
● %=:对于a%=b,即对应于a=a%b。
● &=:对于a&=b,即对应于a=a&b。
● |=:对于a|=b,即对应于a=a|b。
● =:对于a=b,即对应于a=a^b。
● <<=:对于a<<=b,即对应于a=a<<b。
● >>=:对于a>>=b,即对应于a=a>>b。
●>>>=:对于a>>>=b,即对应于a=a>>>b。
相当于赋值和基础运算融合为一个符号。和++符号类似,也是一步并做两步玩儿,挺讨厌的。
位运算符
位运算符号包含以下成分
| 符号 | 含义 | 规则 |
|---|---|---|
| & | 与 | 两个位都为1时,结果为1 |
| | | 或 | 有一个位为1时,结果为1 |
| ^ | 异或 | 0和1异或0都不变,异或1则取反 |
| ~ | 取反 | 0和1全部取反 |
| << | 左移 | 位全部左移若干位,高位丢弃,低位补0 |
| >> | 算术右移 | 位全部右移若干位,高位补k个最高有效位的值 |
| >>> | 逻辑右移 | 位全部右移若干位,高位补0 |
我们来实际用数字感受一下这些运算符的功能
位与&(真真为真 真假为假 假假为假)
4&6
0000 0000 0000 0000 0000 0000 0000 0100
0000 0000 0000 0000 0000 0000 0000 0110
0000 0000 0000 0000 0000 0000 0000 0100
结果:4
位或|(真真为真 真假为真 假假为假)
4|6
0000 0000 0000 0000 0000 0000 0000 0100
0000 0000 0000 0000 0000 0000 0000 0110
0000 0000 0000 0000 0000 0000 0000 0110
结果:6
位非~(取反码)【注:Java中正数的最高位为0,负数最高位为1,即最高位决定正负符号】
~4
0000 0000 0000 0000 0000 0000 0000 0100
1111 1111 1111 1111 1111 1111 1111 1011
解码:先取反码,再补码
0000 0000 0000 0000 0000 0000 0000 0100
0000 0000 0000 0000 0000 0000 0000 0101
结果:-5
位异或^(真真为假 真假为真 假假为假) 只有不一样才能为真
4^6
0000 0000 0000 0000 0000 0000 0000 0100
0000 0000 0000 0000 0000 0000 0000 0110
0000 0000 0000 0000 0000 0000 0000 0010
结果:2
有符号右移>>(若正数,高位补0,负数,高位补1)
-4>>2
1111 1111 1111 1111 1111 1111 1111 1100 原码
1111 1111 1111 1111 1111 1111 1111 1111 右移,最左边空出两位按规则负数空位补1
0000 0000 0000 0000 0000 0000 0000 0000 解码
0000 0000 0000 0000 0000 0000 0000 0001 补码(补码即最后一位+1)
结果:-1
有符号左移<<(若正数,高位补0,负数,高位补1)
-4<<2
1111 1111 1111 1111 1111 1111 1111 1100 原码
1111 1111 1111 1111 1111 1111 1111 0000 左移,最右边空出两位补0
0000 0000 0000 0000 0000 0000 0000 1111 解码
0000 0000 0000 0000 0000 0000 0001 0000 补码
结果:-16
无符号右移>>>(不论正负,高位均补0)
-4>>>2
1111 1111 1111 1111 1111 1111 1111 1100 原码
0011 1111 1111 1111 1111 1111 1111 1111 右移(由于高位均补0,故>>>后的结果一定是正数)
结果:1073741823
其中需要注意的是:
- 位运算只可运用于整数,对于float和double不行。
- 逻辑右移符号各种语言不一样,比如java是>>>。
- 位操作符的运算优先级比较低,尽量使用括号来确保运算顺序。比如1&i+1,会先执行i+1再执行&。
思考一番,为什么会有这样的运算符?我们一个byte是8个位,每个位上只有0,1。这样的结构自然而然就会让人联想到数组。既然是数组,我们就应该有最基本最基本的操作:针对某个位进行修改值。如果需要同时去改多个位,那就变成批量改值,这就需要进行遍历操作。虽说如此,byte是我们计算的最小单元了,没有办法像数组那样很精细化的操作。那么就应该造很多直接操作一个或者多个byte的操作符。这个行为也是计算机组成原理里面那么多元器件很容易搭建出来的操作方式——电路里面有很多逻辑门,很多逻辑门串在一起就可以组织出批量处理位的能力。
继续想,类比于数组,最重要的两个概念是,位置与值,那么对应的我们位运算符应该也包含针对值的处理,和针对位置的处理。从上面的表格内,你就可以发现这样的规律,与或非,异或(也可以由与或非搭建出来,只不过很常用就单独成符号)来批量操作值。左移右移表达位置操作,算数右移主要是因为数值的负号带来的问题。和前文描述的符号扩展息息相关。
我们有了这种批量位运算的算子,我们就可以高效实现一些功能。当然,前文也提到了类比于数组,数组最重要的能力就是精细化修改,我们这种高级的批量运算的算子也应该满足。稍加思考,我们整理出下面的字节操作。
修改特定比特位数上的值
| 位运算 | 功能 | 示例 |
|---|---|---|
| x | (1 << (k-1)) | 把右数第k位变成1 | 101001->101101,k=3 |
| x & ~ (1 << (k-1)) | 把右数第k位变成0 | 101101->101001,k=3 |
| x ^(1 <<(k-1)) | 把右数第k位取反 | 101001->101101,k=3 |
如果K=0,表达修改最后一位,那么式子就可以简写为:
| 位运算 | 功能 | 示例 |
|---|---|---|
| x | 1 | 把最后一位变成1 | 101100->101101 |
| x & -2 | 把最后一位变成0 | 101101->101100 |
| x ^ 1 | 最后一位取反 | 101101->101100 |
获取特定比特位数上的值
| 位运算 | 功能 | 示例 |
|---|---|---|
| x & (1 << k-1) | 取右数第k位 | 1101101->1,k=4 |
| x >> (k-1) & 1 | 取末k位 | 1101101->1101,k=5 |
特殊比特位点执行添加/删除位
| 位运算 | 功能 | 示例 |
|---|---|---|
| x >> 1 | 去掉最后一位 | 101101->10110 |
| x << 1 | 在最后加一个0 | 101101->1011010 |
| x << 1 | 1 | 在最后加一个1 | 101101->1011011 |
byte特殊连续位点处理
| 位运算 | 功能 | 示例 |
|---|---|---|
| x & (x+1) | 把右边连续的1变成0 | 100101111->100100000 |
| x | (x+1) | 把右起第一个0变成1 | 100101111->100111111 |
| x | (x-1) | 把右边连续的0变成1 | 11011000->11011111 |
| (x ^ (x+1)) >> 1 | 取右边连续的1 | 100101111->1111 |
| x & -x | 去掉右起第一个1的左边 | 100101000->1000 |
位运算技巧:向上取2的倍数
/**
* Returns a power of two size for the given target capacity.
*/
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
这里的代码来自于HashMap,目的是获取到大于等于给定值的2的幂指数。这个算法很巧妙,我们来看看是怎么回事儿。像这种机制一眼看不出来就写例子找规律。
int cap = 102413;
int n = cap - 1; // 1100011
System.out.println("n:" + n + " ----- " + Integer.toBinaryString(n));
n |= n >>> 1; // 1110011
System.out.println("n:" + n + " ----- " + Integer.toBinaryString(n));
n |= n >>> 2; // 1111111
System.out.println("n:" + n + " ----- " + Integer.toBinaryString(n));
n |= n >>> 4; // 1111111
System.out.println("n:" + n + " ----- " + Integer.toBinaryString(n));
n |= n >>> 8; // 1111111
System.out.println("n:" + n + " ----- " + Integer.toBinaryString(n));
n |= n >>> 16; // 1111111
System.out.println("n:" + n + " ----- " + Integer.toBinaryString(n));
int ret = (n < 0) ? 1 : (n >= Integer.MAX_VALUE) ? Integer.MAX_VALUE : n + 1;
System.out.println(ret);
获得到输出为:
n:102412 ----- 11001000000001100
n:120846 ----- 11101100000001110
n:130575 ----- 11111111000001111
n:131055 ----- 11111111111101111
n:131071 ----- 11111111111111111
n:131071 ----- 11111111111111111
131072
这样一来很容易就会发现一个规律:
n |= n >>> 1; 会把原来位数中是1的位数后面的1位也置为1 //经过这一步之后,所有的1都是连续的,不会有010这样的了,
n |= n >>> 2; 会把原来位数中是1的位数后面的2位也置为1 //经过这一步之后,所有的1都是至少4个连续的了,至少是1111这样的
n |= n >>> 4; 会把原来位数中是1的位数后面的4位也置为1 //经过这一步之后,所有的1都是至少8个连续的了,至少是11111111这样的
n |= n >>> 8; 会把原来位数中是1的位数后面的8位也置为1 //经过这一步之后,所有的1都是至少16个连续的了,至少是1111111111111111这样的
n |= n >>> 16; 会把原来位数中是1的位数后面的16位也置为1 //到这一步之后,1至少是32位连续的了,而且往往来不及到这一步,前面几步骤之后就全部置1了
最后返回n+1,肯定是一个2的幂次,因为全部是1的数字恰好就是比2的幂次少1;为什么要执行int n = cap - 1;这是考虑都输入刚好是2的幂次的情况,比如输入刚好是1024,如果不执行减1操作,那么输出就是2048了,减去1之后,输出还是1024。
上面解释了为什么返回的结果是2的幂次,因为他得到的是全1的二进制数最后加1,那么为什么刚好是大于输出参数的最小的2的幂次数呢?回头看看会发现,如果输入的数字位数是5位,那么这个计算的过程中并不会改变他的位数,而会得到11111,最后加1,因此得到的是大于这个数字的2的最小幂次数,如果输入的是11111,那运算的过程中不会改变,最后直接返回加1的结果,到这里就弄清楚了。
位运算技巧:使用位运算代替取模
X % 2^n = X & (2^n – 1)
假设n为3,则2^3 = 8,表示成2进制就是1000。2^3 -1 = 7 ,即0111。此时X & (2^3 – 1) 就相当于取X的2进制的最后三位数。
从2进制角度来看,X / 8相当于 X >> 3,即把X右移3位,此时得到了X / 8的商,而被移掉的部分(后三位),则是X % 8,也就是余数。
例如:10 & 8 = 2 ,10 & 7 = 2
位运算技巧:不需要额外变量交换两个整数的值
a = a ^ b;
b = a ^ b;
a = a ^ b;
假设a异或b的结果记为c, c就是a整数位信息和b整数位信息的所有不同信息。比如,a=4=100, b=3=011, a^b=c=000。
a异或c的结果就是b。比如a=4=100, c=111, a^c=011=3=b。
b异或c的结果就是a。比如b=3=011, c=111, b^c=100=4=a。
所以,在执行上面三行代码之前,假设有a信息和b信息。执行完第一行代码之后,a变成了c, b还是b;执行完第二行代码之后,a仍然是c, b变成了a;执行完第三行代码之后, a变成了b, b仍然是a。过程结束。
二进制逆序
int reverse_order(int n){
n = ((n & 0xAAAAAAAA) >> 1) | ((n & 0x55555555) << 1);
n = ((n & 0xCCCCCCCC) >> 2) | ((n & 0x33333333) << 2);
n = ((n & 0xF0F0F0F0) >> 4) | ((n & 0x0F0F0F0F) << 4);
n = ((n & 0xFF00FF00) >> 8) | ((n & 0x00FF00FF) << 8);
n = ((n & 0xFFFF0000) >> 16) | ((n & 0x0000FFFF) << 16);
return n;
}
二分查找32位整数前导0个数
int nlz(int x){
int n;
if (x == 0) return(32);
n = 1;
if ((x >> 16) == 0) {n = n +16; x = x <<16;}
if ((x >> 24) == 0) {n = n + 8; x = x << 8;}
if ((x >> 28) == 0) {n = n + 4; x = x << 4;}
if ((x >> 30) == 0) {n = n + 2; x = x << 2;}
n = n - (x >> 31);
return n;
}
求绝对值
int abs(int a) {
int i = a >> 31;
return ((a ^ i) - i);
}
二进制中1的个数
int BitCount_e(unsigned int value) {
int count = 0;
// 解释下下面这句话代码,这句话求得两两相加的结果,例如 11 01 00 10
// 11 01 00 10 = 01 01 00 00 + 10 00 00 10,即由奇数位和偶数位相加而成
// 记 value = 11 01 00 10,high_v = 01 01 00 00, low_v = 10 00 00 10
// 则 value = high_v + low_v,high_v 右移一位得 high_v_1,
// 即 high_v_1 = high_v >> 1 = high_v / 2
// 此时 value 可以表示为 value = high_v_1 + high_v_1 + low_v,
// 可见 我们需要 high_v + low_v 的和即等于 value - high_v_1
// 写简单点就是 value = value & 0x55555555 + (value >> 1) & 0x55555555;
value = value - ((value >> 1) & 0x55555555);
// 之后的就好理解了
value = (value & 0x33333333) + ((value >> 2) & 0x33333333);
value = (value & 0x0f0f0f0f) + ((value >> 4) & 0x0f0f0f0f);
value = (value & 0x00ff00ff) + ((value >> 4) & 0x00ff00ff);
value = (value & 0x0000ffff) + ((value >> 8) & 0x0000ffff);
return value;
// 另一种写法,原理一样
//value = (value & 0x55555555) + (value >> 1) & 0x55555555;
//value = (value & 0x33333333) + ((value >> 2) & 0x33333333);
//value = (value & 0x0f0f0f0f) + ((value >> 4) & 0x0f0f0f0f);
//value = value + (value >> 8);
//value = value + (value >> 16);
//return (value & 0x0000003f);
比较运算符
比较运算符用于比较两个数值之间的大小,其运算结果为一个逻辑类型(boolean布尔类型)的数值。写法上基本和数学一致,分别是:
== (等于) ,!=(不等于),>(大于),>=(大于等于),<(小于),<=(小于等于)
System.out.println("9.5<8 :"+(9.5<8));
System.out.println("8.5<=8.5:"+(8.5<=8.5));
System.out.println("a~z:"+((int)'a')+"~"+((int)'z'));
System.out.println("A~Z:"+((int)'A')+"~"+((int)'Z'));
System.out.println("'A' < 'a':"+('A' < 'a'));//字符'A'的Unicode编码值小于字符'a'
输出结果为:
9.5<8 :false
8.5<=8.5:true
a~z:97~122
A~Z:65~90
'A' < 'a':true
其中boolean类型只能比较相等和不相等,不能比较大小;
逻辑运算符
逻辑运算的数据和逻辑运算符的运算结果是boolean类型。
第一组:逻辑与:&&,逻辑或:||,逻辑非:!,逻辑异或: ^,
第二组:不短路与:&,不短路或|
两组运算符功能一样,只不过第二组是不短路的计算。
所谓短路计算,是指系统从左至右进行逻辑表达式的计算,一旦出现计算结果已经确定的情况,则计算过程即被终止。
a)对于&&运算来说,只要运算符左端的值为false,则因无论运算符右端的值为true或为false,其最终结果都为false。
所以,系统一旦判断出&&运算符左端的值为false,则系统将终止其后的计算过程;
b)对于 || 运算来说,只要运算符左端的值为true,则因无论运算符右端的值为true或为false,其最终结果都为true。
所以,系统一旦判断出|| 运算符左端的值为true,则系统将终止其后的计算过程。
下面代码示范了逻辑运算符短路与不短路的区别(以|和||的区别为例):
int a = 3;
int b = 9;
if(a>2 | b++ >9){
//输出10,说明b++ >9得到了计算
System.out.println(b);
}
if(a>2 || b++ >9){
//输出9,说明b++ > 9没有得到了计算
System.out.println(b);
}
与逻辑运算符息息相关的就是逻辑代数了,逻辑代数是数学里面的小分支,专门拿来做逻辑运算的。门电路搭建出译码器或多或少都需要使用逻辑代数进行化简。而我们的代码如果遇到特别复杂的判断逻辑,也可以使用逻辑代数的方式进行简化,简化后的式子可能很精简,但是会丢失阅读性。
公式参考如下:相关应用将会在计算机组成原理模块详细描述,一般代码用不到
| 名称 | 公式 |
|---|---|
| 交换律 | A+B = B+1 |
A*B = B*A | |
| 结合律 | A+(B+C) = (A + B)+C |
A*(B*C) = (A*B)*C | |
| 分配律 | A+BC = (A+B)(A+C) |
A(B+C) = AB + AC | |
| 互补律 | A + A' = 1 |
AA' = 0 | |
| 0-1律 | A+0 = A |
A+1 = 1 | |
A*1 = A | |
A*0 = 0 | |
| 对合律 | A'' = A |
| 重叠律 | A + A = A |
A*A = A | |
| 吸收率 | A+AB = A |
A+A'B = A+B | |
AB+AB' = A | |
A(A+B) =A | |
A(A'+B) = AB | |
(A+B)(A+B')=A | |
| 包含率 | A*B + A'*C +B*C = AB+A'*C |
(A+B)*(A'+C)*(B+C)=(A+B)*(A'+C) | |
| 反演率 | (A+B)' = A'B' |
(A*B)'=A' + B' |
+指的是或(||)'指的是取反(!)*指的是且(&&)
三目运算符
该运算符的语法是:判断条件 ? 表达式 1 : 表达式2
可以说这个运算符是最复杂的运算符了,有三个入参。这个运算符的出现,可以帮助我们缩减一些简单的语句,其含义是等价的:
if(a<b)
min=a;
else
min=b;
上面一大块儿的语句可以缩减为一句:min=(a<b)?a:b; 看上去就清爽很多,而且容易理解。但是这里应该要有个原则,但凡不是一眼就能看明白的分支语句,就应该使用if,而不是三目运算符。
针对三目运算符,还有一些神奇的现象:
boolean condition = false;
Double value1 = 1.0D;
Double value2 = 2.0D;
Double value3 = null;
Double result = condition ? value1 * value2 : value3;
这样是会抛出抛出空指针异常的,神不神奇?本质上是三目运算碰上了类型转换导致的不可思议。没法简单的看到问题的本质,又只能借助于字节码的力量:
17 iload_1 [condition]
18 ifeq 33
21 aload_2 [value1]
22 invokevirtual java.lang.Double.doubleValue() : double [24]
25 aload_3 [value2]
26 invokevirtual java.lang.Double.doubleValue() : double [24]
29 dmul
30 goto 38
33 aload 4 [value3]
35 invokevirtual java.lang.Double.doubleValue() : double [24]
38 invokestatic java.lang.Double.valueOf(double) : java.lang.Double [16]
41 astore 5 [result]
43 getstatic java.lang.System.out : java.io.PrintStream [28]
46 aload 5 [result]
在第 33 行,加载 Double 对象 value3 到操作数栈中;在第 35 行,调用 Double 对象 value3 的 doubleValue 方法。这个时候,由于 value3 是空对象 null ,调用 doubleValue 方法必然抛出抛出空指针异常。但是,为什么要把空对象 value3 转化为基础数据类型 double ?这里背后蕴含着好几个规则:
- 若两个表达式类型相同,返回值类型为该类型;
- 若两个表达式类型不同,但类型不可转换,返回值类型为Object类型;
- 若两个表达式类型不同,但类型可以转化,先把包装数据类型转化为基本数据类型,然后按照基本数据类型的转换规则(byte<short(char)<int<long<float<double)来转化,返回值类型为优先级最高的基本数据类型。
根据规则分析,表达式 1(value1 * value2)计算后返回基础数据类型 double ,表达式 2(value3) 返回包装数据类型 Double ,根据三元表达式的类型转化规则判断,最终的返回类型为基础数据类型 double 。所以,当条件表达式 condition 等于 false 时,需要把空对象 value3 转化为基础数据类型 double ,于是就调用了 value3 的 doubleValue 方法抛出了空指针异常。
如此一来,按照测试的手段进行测试上面的机制:
boolean condition = false;
Double value1 = 1.0D;
Double value2 = 2.0D;
Double value3 = null;
Integer value4 = null;
// 返回类型为Double,不抛出空指针异常
Double result1 = condition ? value1 : value3;
// 返回类型为double,会抛出空指针异常
Double result2 = condition ? value1 : value4;
// 返回类型为double,不抛出空指针异常
Double result3 = !condition ? value1 * value2 : value3;
// 返回类型为double,会抛出空指针异常
Double result4 = condition ? value1 * value2 : value3;
如此很好的验证了我们的想法。
运算符优先级
优先级说到底是人设计出来的,是一种内含在语言内部的规范。你那么写,计算机就按照之前的约定,理解代码,该怎么干怎么干。
参考 https://github.com/antlr/grammars-v4/blob/master/java/java8/Java8Lexer.g4,这是java的g4文件,描述了java代码的语法树规则。antlt可以吃掉一份规范文件,给你造出词法解析器,语法分析器。从这个意义上来讲,anlrt是元编程的产物,很厉害。
这里只需要有一个大局的概念:任何语言规范都是人制造出来的,都要符合人的思维,而人的思维恰恰又是可以推演的
ASSIGN : '=';
GT : '>';
LT : '<';
BANG : '!';
TILDE : '~';
QUESTION : '?';
COLON : ':';
EQUAL : '==';
LE : '<=';
GE : '>=';
NOTEQUAL : '!=';
AND : '&&';
OR : '||';
INC : '++';
DEC : '--';
ADD : '+';
SUB : '-';
MUL : '*';
DIV : '/';
BITAND : '&';
BITOR : '|';
CARET : '^';
MOD : '%';
ARROW : '->';
COLONCOLON : '::';
ADD_ASSIGN : '+=';
SUB_ASSIGN : '-=';
MUL_ASSIGN : '*=';
DIV_ASSIGN : '/=';
AND_ASSIGN : '&=';
OR_ASSIGN : '|=';
XOR_ASSIGN : '^=';
MOD_ASSIGN : '%=';
LSHIFT_ASSIGN : '<<=';
RSHIFT_ASSIGN : '>>=';
URSHIFT_ASSIGN : '>>>=';
这种语法文件,会有个规矩,放在下面的优先级会高一些。因此直接参考这份文件就可以明白它的优先级应该是什么了。
总结
这篇详细描述了组成语言的最小能力集合,所有语言都需要具备这些能力,语法结构可能不一样,但是都是语义级别的。计算机要识别你的含义,意味着你的语言所承载的信息量必须是足够的。而信息的组成可以不一样,甚至可以在信息里面添加校验(也是静态语言自带的一种机制,可以在编译器,自我检测当前代码是否有问题,不需要在运行时暴露)。