Bootstrap

图的广度优先搜索（bfs）以及深度优先搜索（dfs）

1.前言

和树的遍历类似，图的遍历也是从图中某点出发，然后按照某种方法对图中所有顶点进行访问，且仅访问一次。

但是图的遍历相对树而言要更为复杂。因为图中的任意顶点都可能与其他顶点相邻，所以在图的遍历中必须记录已被访问的顶点，避免重复访问。

根据搜索路径的不同，我们可以将遍历图的方法分为两种：广度优先搜索和深度优先搜索。
2.图的基本概念
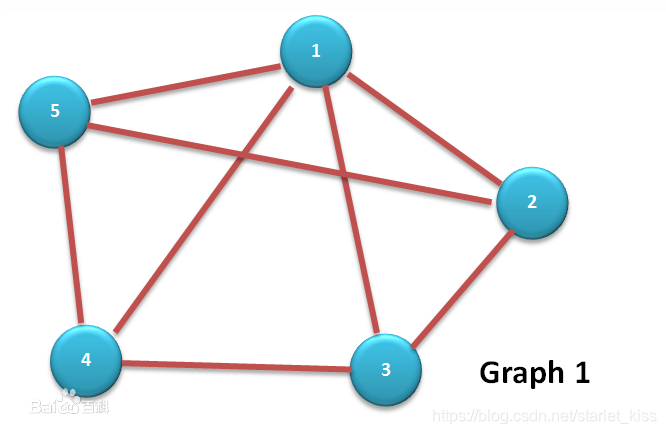
无向图：顶点对(u，v)是无序的，即（u，v）和（v，u）是同一条边。常用一对圆括号表示。如图所示：
在这里插入图片描述
有向图：顶点对<u,v>是有序的，它是指从顶点u到顶点 v的一条有向边。其中u是有向边的始点，v是有向边的终点。常用一对<>表示。如图所示:
在这里插入图片描述
连通图：在无向图G中，从顶点v到顶点v’有路径，则称v和v’是联通的。若图中任意两顶点v、v’∈V，v和v’之间均联通，则称G是连通图。上述两图均为连通图。如图所示：
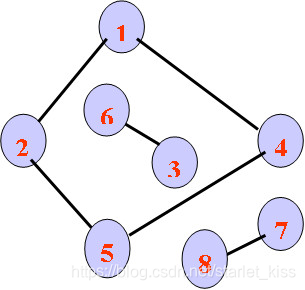
在这里插入图片描述
非连通图：若无向图G中，存在v和v’之间不连通，则称G是非连通图。如图所示：
在这里插入图片描述
3.广度优先搜索
基本思想：宽度优先搜索算法（又称广度优先搜索）是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。
广度优先搜索算法的搜索步骤一般是：
（1）从队列头取出一个结点，检查它按照扩展规则是否能够扩展，如果能则产生一个新结点。
（2）检查新生成的结点，看它是否已在队列中存在，如果新结点已经在队列中出现过，就放弃这个结点，然后回到第（1）步。否则，如果新结点未曾在队列中出现过，则将它加入到队列尾。
（3）检查新结点是否目标结点。如果新结点是目标结点，则搜索成功，程序结束；若新结点不是目标结点，则回到第（1）步，再从队列头取出结点进行扩展。
最终可能产生两种结果：找到目标结点，或扩展完所有结点而没有找到目标结点。
如果目标结点存在于解答树的有限层上，广度优先搜索算法一定能保证找到一条通向它的最佳路径，因此广度优先搜索算法特别适用于只需求出最优解的问题。当问题需要给出解的路径，则要保存每个结点的来源，也就是它是从哪一个节点扩展来的。
对于广度优先搜索算法来说，问题不同则状态结点的结构和结点扩展规则是不同的，但搜索的策略是相同的。
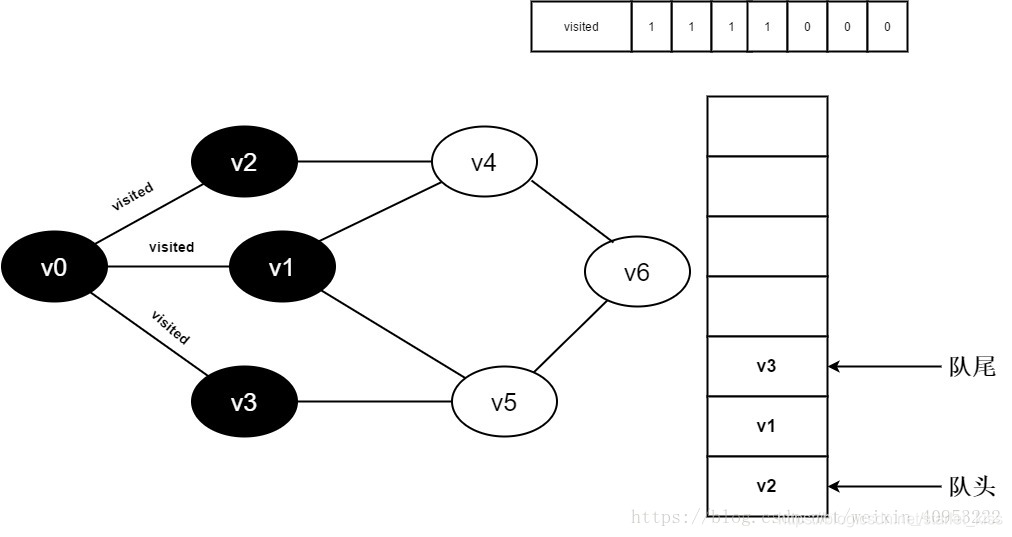
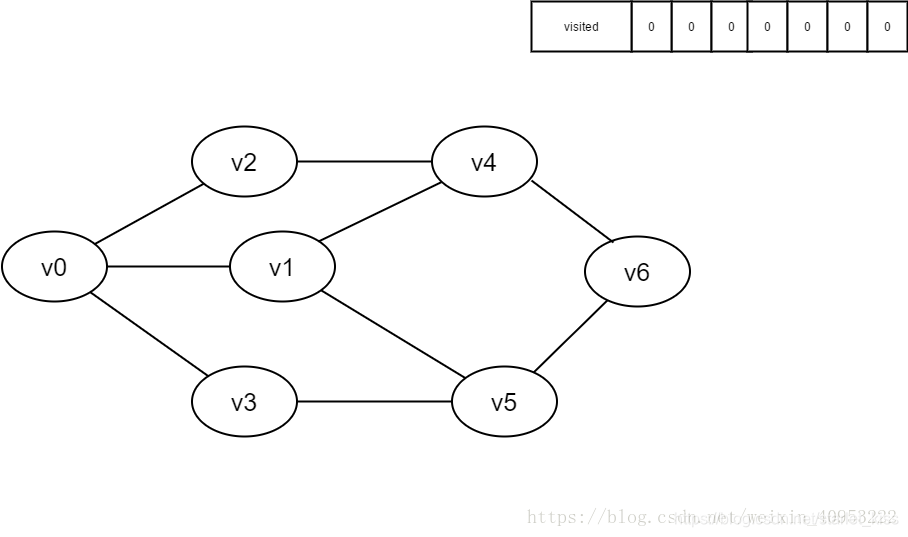
广度优先搜索如图所示：
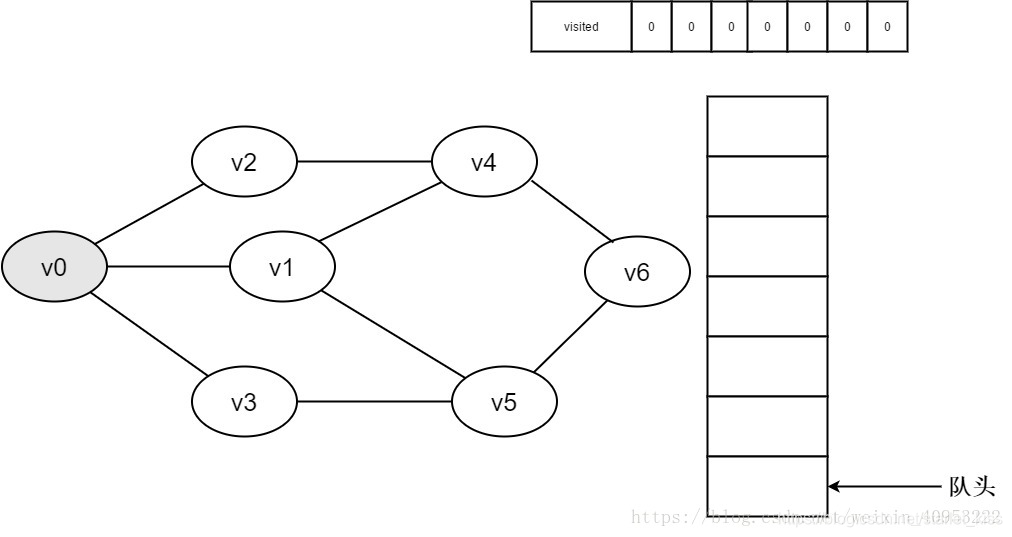
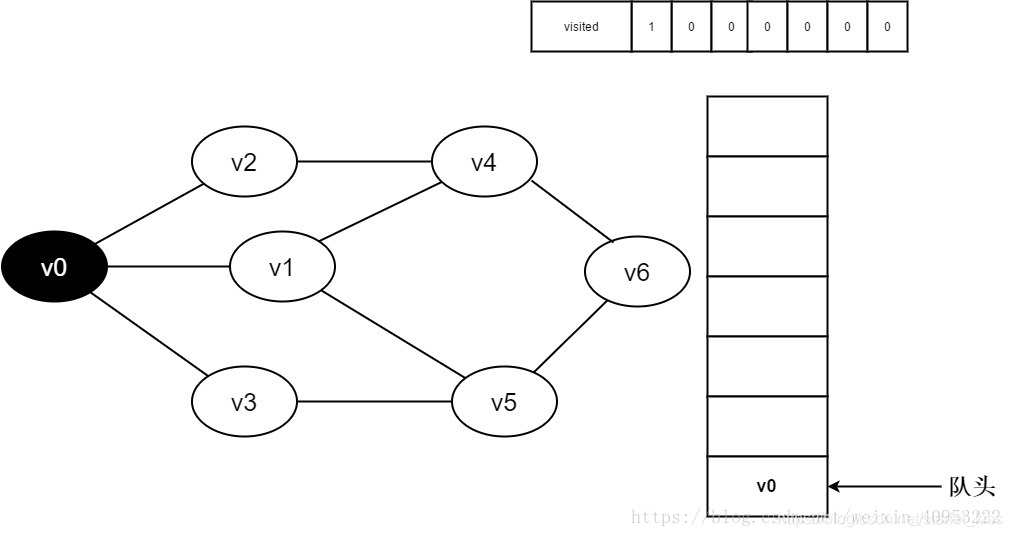
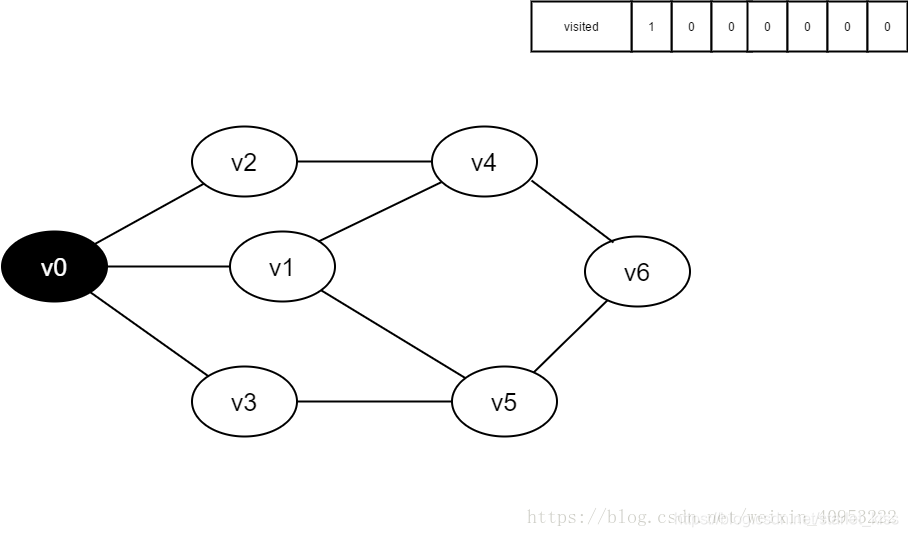
1.初始时全部顶点均未被访问，visited数组初始化为0，队列中没有元素。
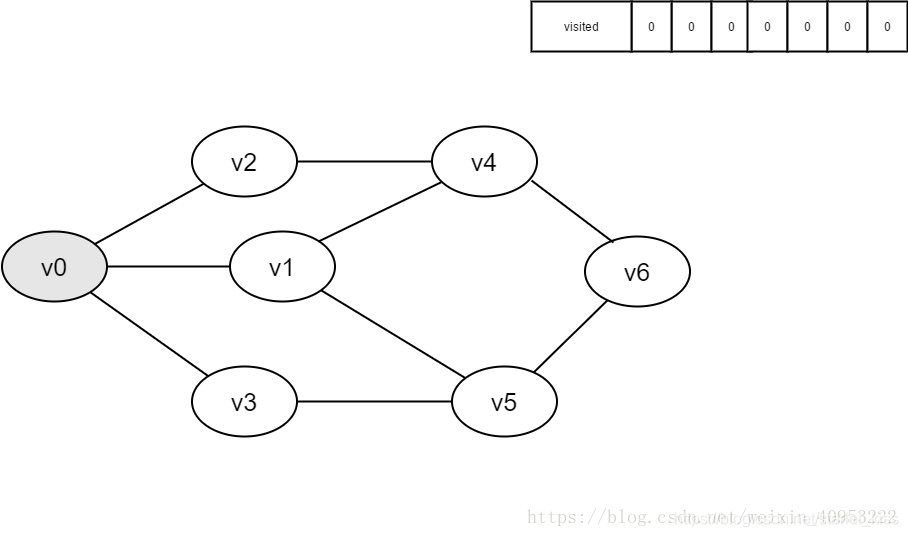
在这里插入图片描述
2.即将访问顶点v0。
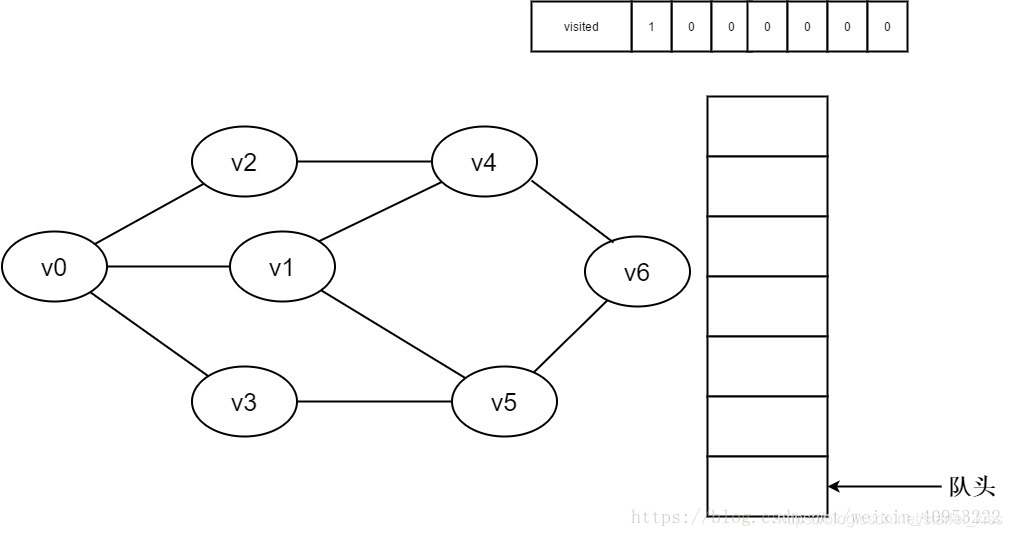
在这里插入图片描述
3.访问顶点v0，并置visited[0]的值为1，同时将v0入队。
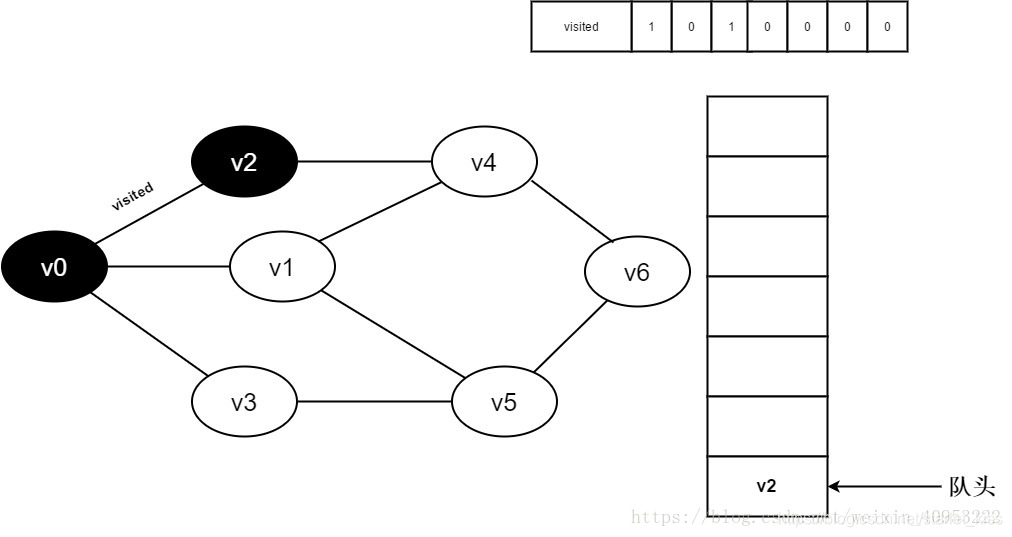
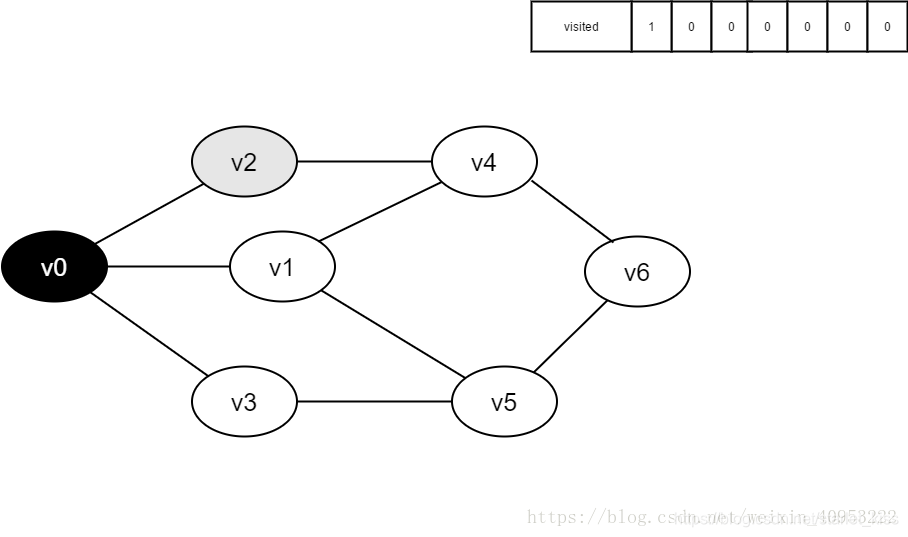
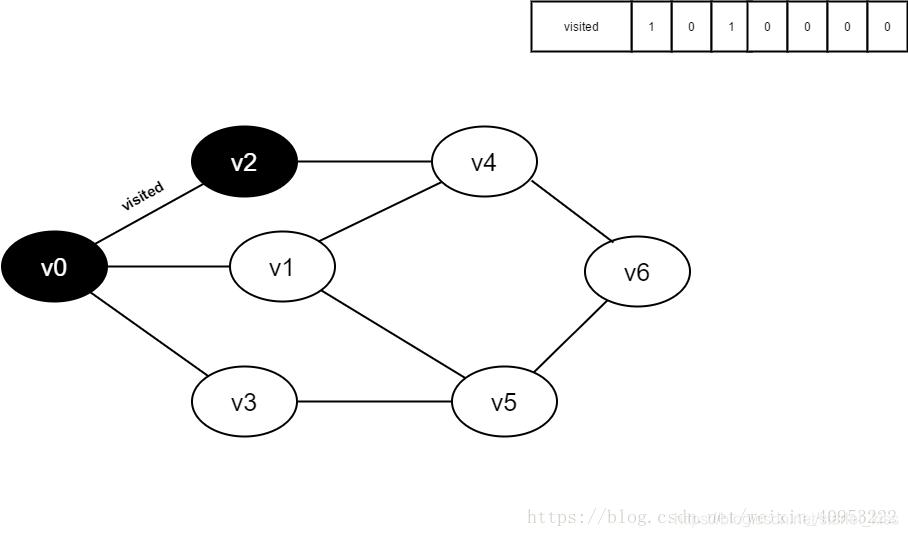
在这里插入图片描述
4.将v0出队，访问v0的邻接点v2。判断visited[2]，因为visited[2]的值为0，访问v2。
在这里插入图片描述
5.将visited[2]置为1，并将v2入队。
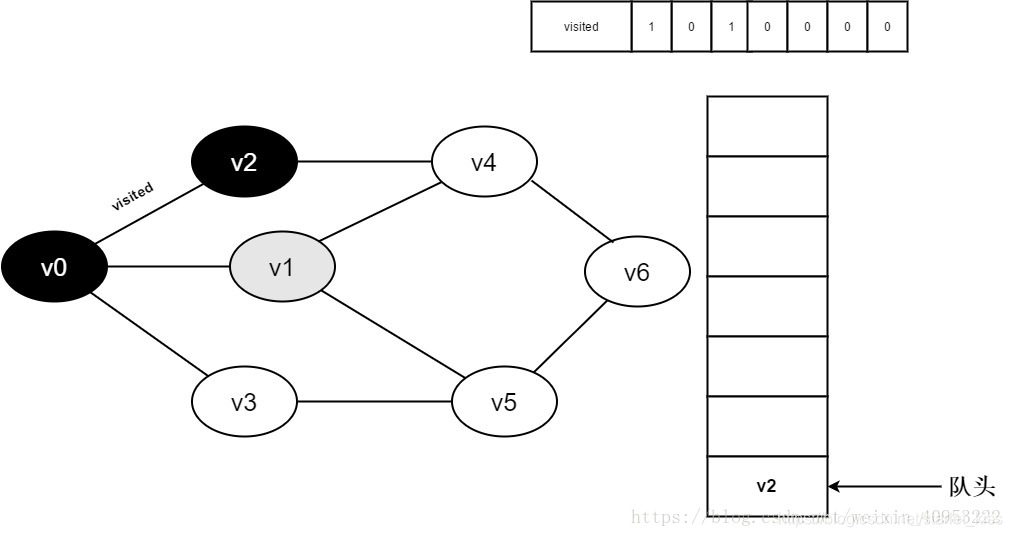
在这里插入图片描述
6.访问v0邻接点v1。判断visited[1],因为visited[1]的值为0，访问v1。
在这里插入图片描述
7.将visited[1]置为0，并将v1入队。
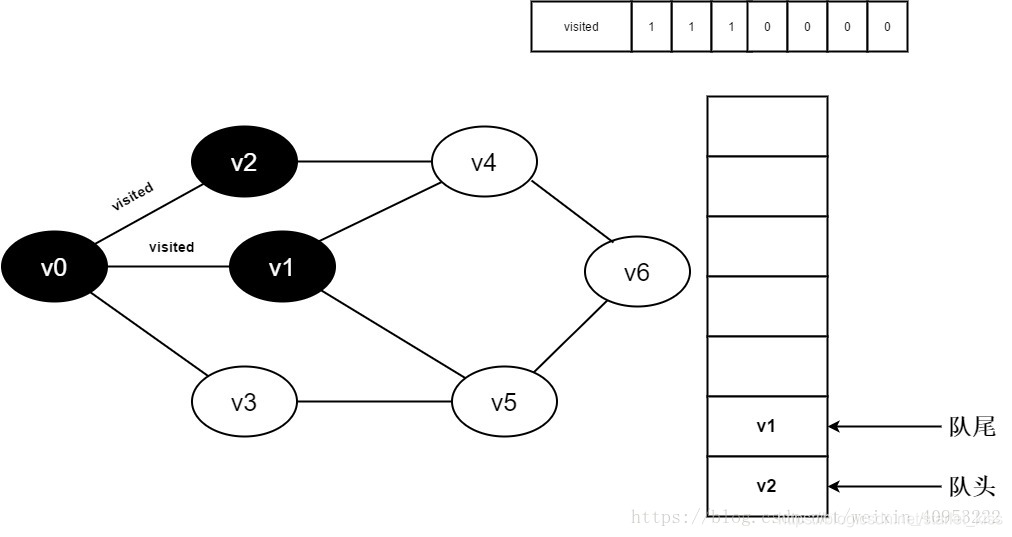
在这里插入图片描述
8.判断visited[3],因为它的值为0，访问v3。将visited[3]置为0，并将v3入队。
在这里插入图片描述
9.v0的全部邻接点均已被访问完毕。将队头元素v2出队，开始访问v2的所有邻接点。

开始访问v2邻接点v0，判断visited[0]，因为其值为1，不进行访问。

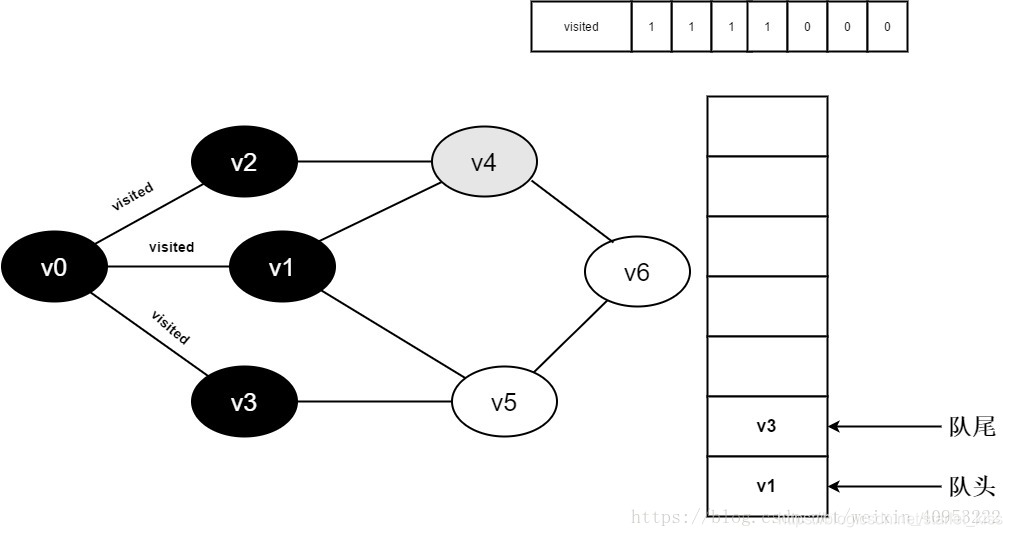
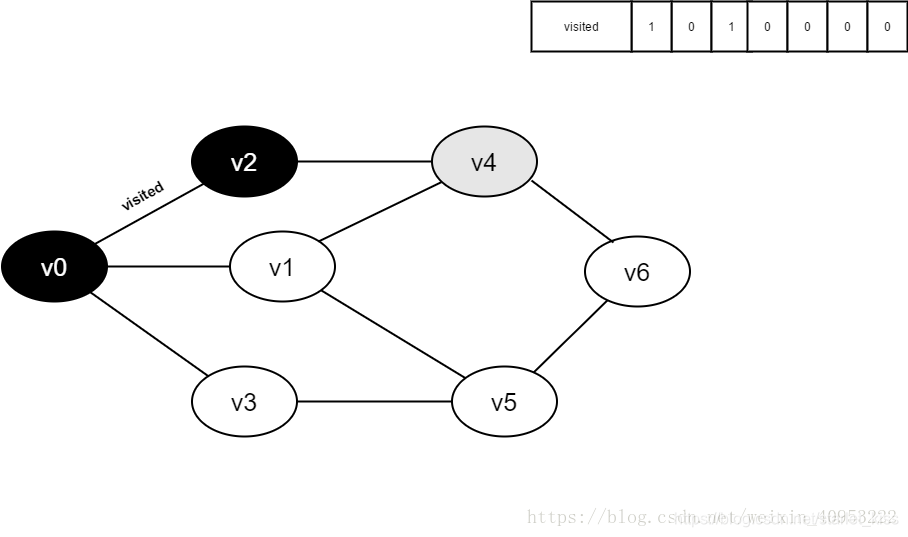
继续访问v2邻接点v4，判断visited[4]，因为其值为0，访问v4，如下图：
在这里插入图片描述
10.将visited[4]置为1，并将v4入队。
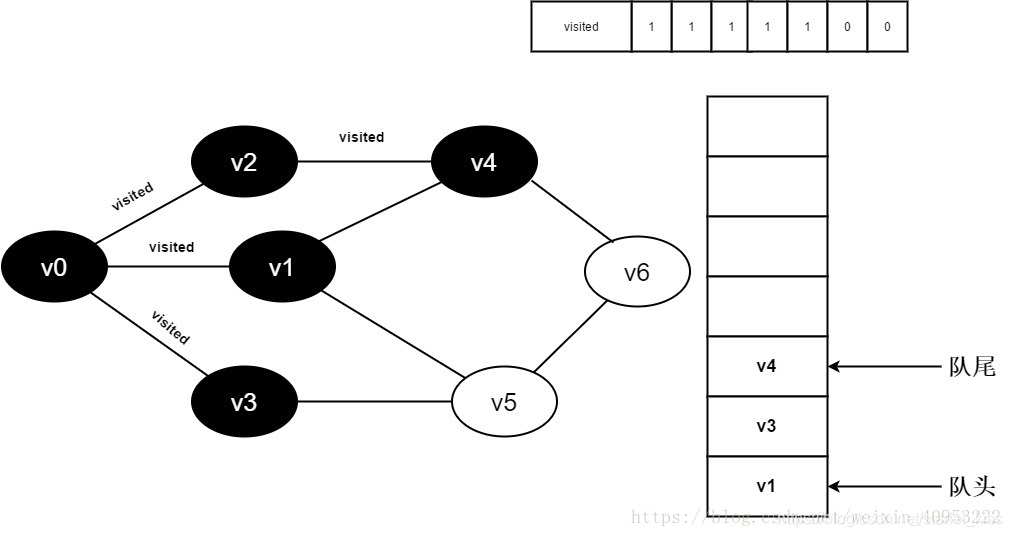
在这里插入图片描述
11.v2的全部邻接点均已被访问完毕。将队头元素v1出队，开始访问v1的所有邻接点。

开始访问v1邻接点v0，因为visited[0]值为1，不进行访问。

继续访问v1邻接点v4，因为visited[4]的值为1，不进行访问。

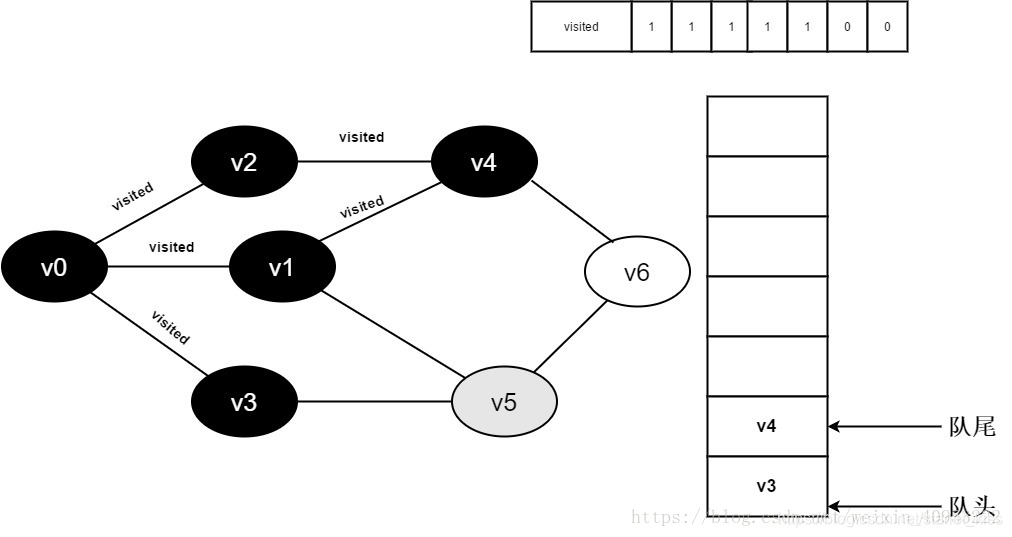
继续访问v1邻接点v5，因为visited[5]值为0，访问v5，如下图：
在这里插入图片描述
12.将visited[5]置为1，并将v5入队。
在这里插入图片描述
13.v1的全部邻接点均已被访问完毕，将队头元素v3出队，开始访问v3的所有邻接点。

开始访问v3邻接点v0，因为visited[0]值为1，不进行访问。

继续访问v3邻接点v5，因为visited[5]值为1，不进行访问。
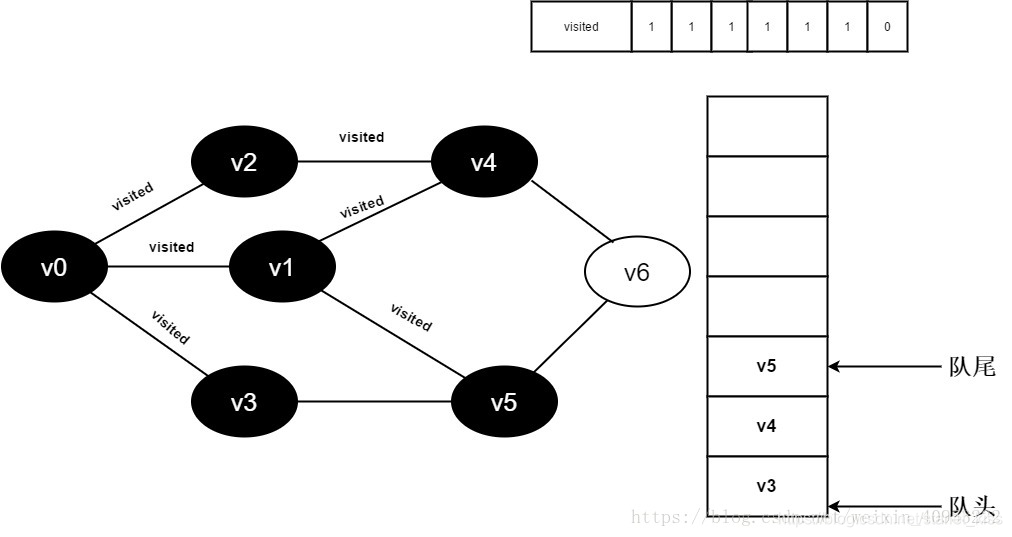
在这里插入图片描述
14.v3的全部邻接点均已被访问完毕，将队头元素v4出队，开始访问v4的所有邻接点。

开始访问v4的邻接点v2，因为visited[2]的值为1，不进行访问。

继续访问v4的邻接点v6，因为visited[6]的值为0，访问v6，如下图：
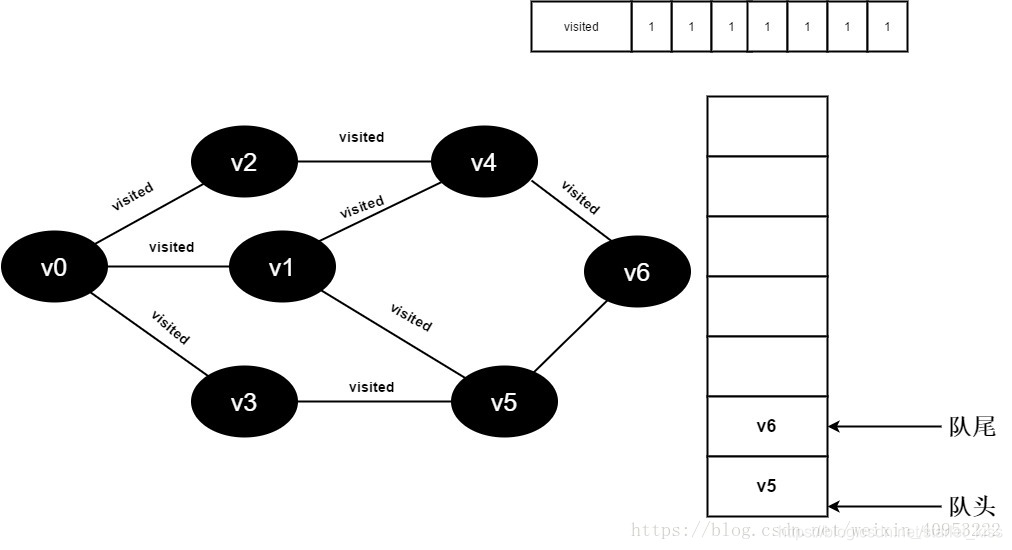
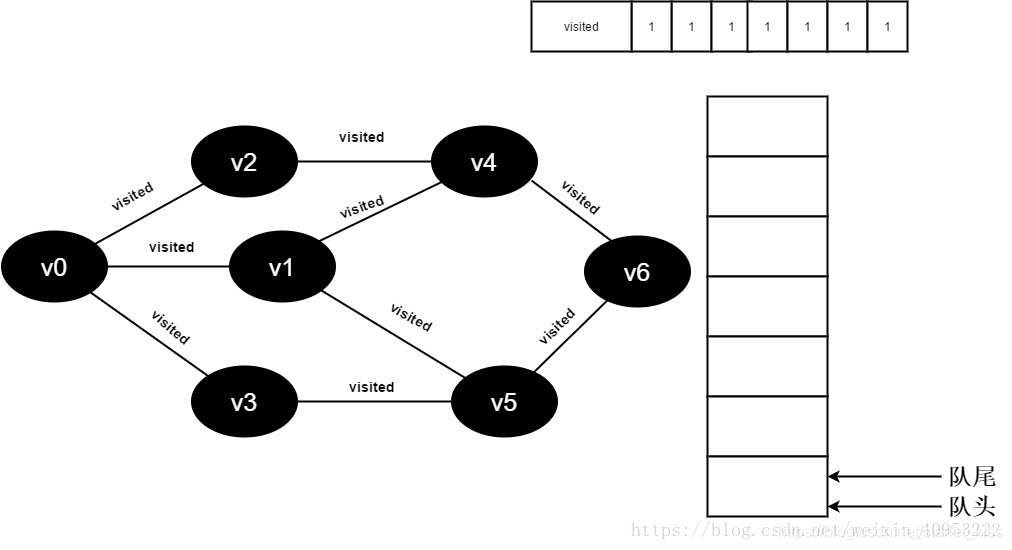
在这里插入图片描述
15.将visited[6]值为1，并将v6入队。
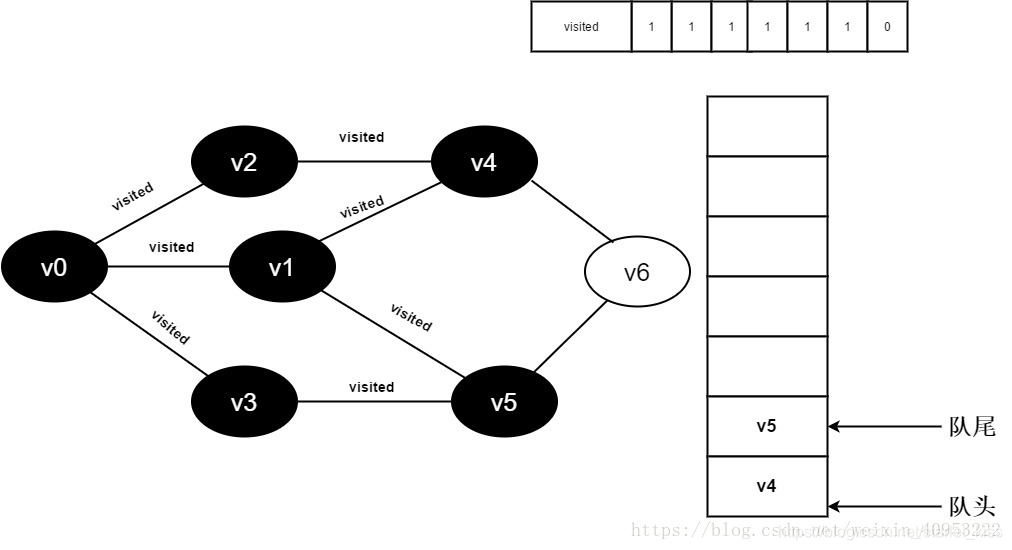
在这里插入图片描述
16.v4的全部邻接点均已被访问完毕，将队头元素v5出队，开始访问v5的所有邻接点。

开始访问v5邻接点v3，因为visited[3]的值为1，不进行访问。

继续访问v5邻接点v6，因为visited[6]的值为1，不进行访问
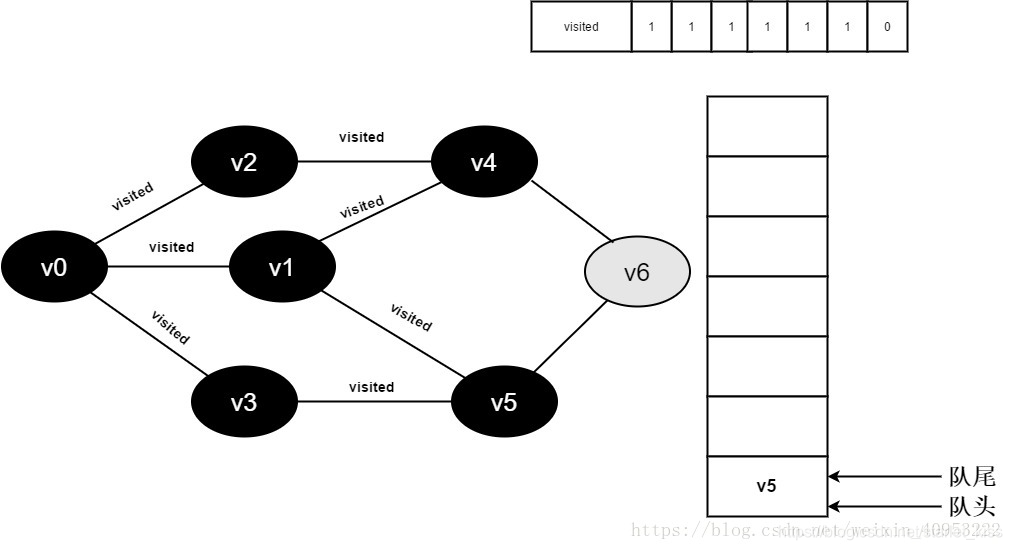
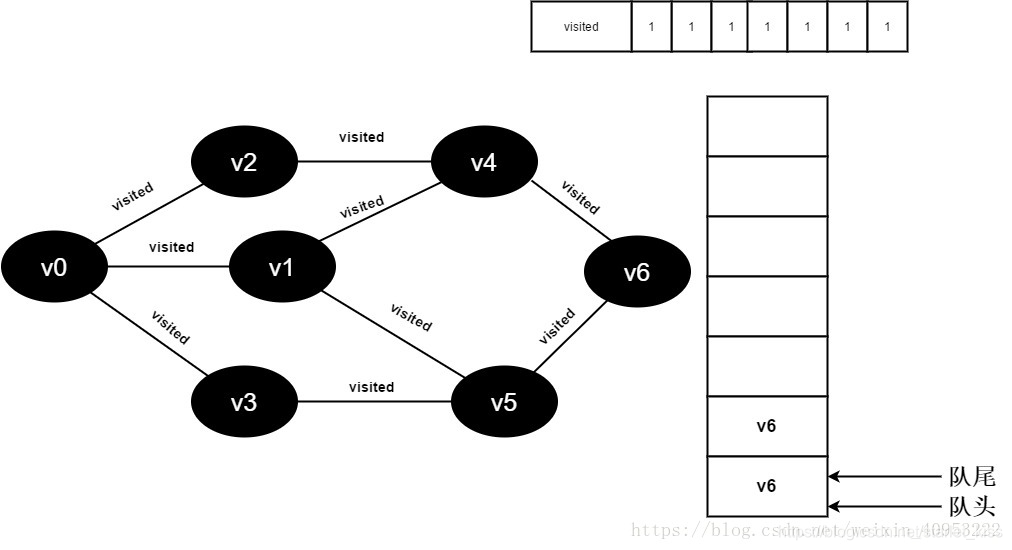
在这里插入图片描述
17.v5的全部邻接点均已被访问完毕，将队头元素v6出队，开始访问v6的所有邻接点。

开始访问v6邻接点v4，因为visited[4]的值为1，不进行访问。

继续访问v6邻接点v5，因为visited[5]的值文1，不进行访问。
在这里插入图片描述
18.队列为空，退出循环，全部顶点均访问完毕。
在这里插入图片描述
广度优先搜索例题：
【例一】 有一个宽为W、高为H的矩形平面，用黑色和红色两种颜色的方砖铺满。一个小朋友站在一块黑色方块上开始移动，规定移动方向有上、下、左、右四种，且只能在黑色方块上移动（即不能移到红色方块上）。编写一个程序，计算小朋友从起点出发可到达的所有黑色方砖的块数（包括起点）。
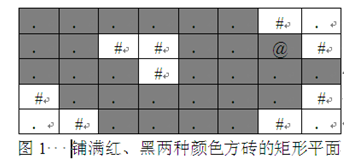
例如，如图1所示的矩形平面中，“#”表示红色砖块，“．”表示黑色砖块，“@”表示小朋友的起点，则小朋友能走到的黑色方砖有28块。
在这里插入图片描述
代码如下：

#include <iostream>
using namespace std;

#define N 21
struct Node
{
    int x;
    int y;
};

int dx[4]={-1,1,0,0};
int dy[4]={0,0,-1,1};
char map[N][N];
int visit[N][N];
int bfs(int startx, int starty,int w,int h)
{
	Node q[N*N],cur,next;   // q为队列
       int  front,rear;        // front为队头指针，rear为队尾指针
       int i,x,y,sum;    
       front=rear=0;           // 队列q初始化
       sum=0;
       cur.x=startx;   cur.y=starty; 
       visit[startx][starty]=1;
       q[rear++]=cur;          // 初始结点入队
       while(rear!=front)      // 队列不为空
       {
              cur=q[front++];     // 队头元素出队
              sum++;              // 方砖计数
              for (i=0;i<4;i++)
              {
                  x=cur.x+dx[i];  y=cur.y+dy[i];
                 if(x >=0 && x<h && y>=0 && y<w && map[x][y]!='#' && visit[x][y]==0)
                 {
                        visit[x][y] = 1;
                        next.x=x;  next.y=y;  // 由cur扩展出新结点next
                        q[rear++]=next;       // next结点入队
                  } 
              }
       }
       return sum;
}

int main()
{
   int i,j,pos_x,pos_y,w,h,sum;
   while(1)
   {
    cin>>w>>h; 
    if(w==0 && h==0) break;
       for(i=0;i<h;i++)
       {
        	for(j=0;j<w;j++)
	        {
				cin>>map[i][j];
	            if(map[i][j]=='@')
	            {
	               pos_x = i;
	               pos_y = j;
	            }
	            visit[i][j] = 0;
	        }
      }
      sum=bfs(pos_x, pos_y,w,h);
      cout<<sum<<endl;
   }
   return 0;
}

4.深度优先搜索
基本思想：深度优先搜索是一种在开发爬虫早期使用较多的方法。它的目的是要达到被搜索结构的叶结点(即那些不包含任何超链的HTML文件) 。在一个HTML文件中，当一个超链被选择后，被链接的HTML文件将执行深度优先搜索，即在搜索其余的超链结果之前必须先完整地搜索单独的一条链。深度优先搜索沿着HTML文件上的超链走到不能再深入为止，然后返回到某一个HTML文件，再继续选择该HTML文件中的其他超链。当不再有其他超链可选择时，说明搜索已经结束。
深度优先搜索DFS（Depth First Search）是从初始结点开始扩展，扩展顺序总是先扩展最新产生的结点。这就使得搜索沿着状态空间某条单一的路径进行下去，直到最后的结点不能产生新结点或者找到目标结点为止。当搜索到不能产生新的结点的时候，就沿着结点产生顺序的反方向寻找可以产生新结点的结点，并扩展它，形成另一条搜索路径。
为了便于进行搜索，要设置一个表存储所有的结点。由于在深度优先搜索算法中，要满足先生成的结点后扩展的原则，所以存储结点的表一般采用栈这种数据结构。
深度优先搜索算法的搜索步骤一般是：
（1）从初始结点开始，将待扩展结点依次放到栈中。
（2）如果栈空，即所有待扩展结点已全部扩展完毕，则问题无解，退出。
（3）取栈中最新加入的结点，即栈顶结点出栈，并用相应的扩展原则扩展出所有的子结点，并按顺序将这些结点放入栈中。若没有子结点产生，则转（2）。
（4）如果某个子结点为目标结点，则找到问题的解（这不一定是最优解），结束。如果要求得问题的最优解，或者所有解，则转（2），继续搜索新的目标结点。
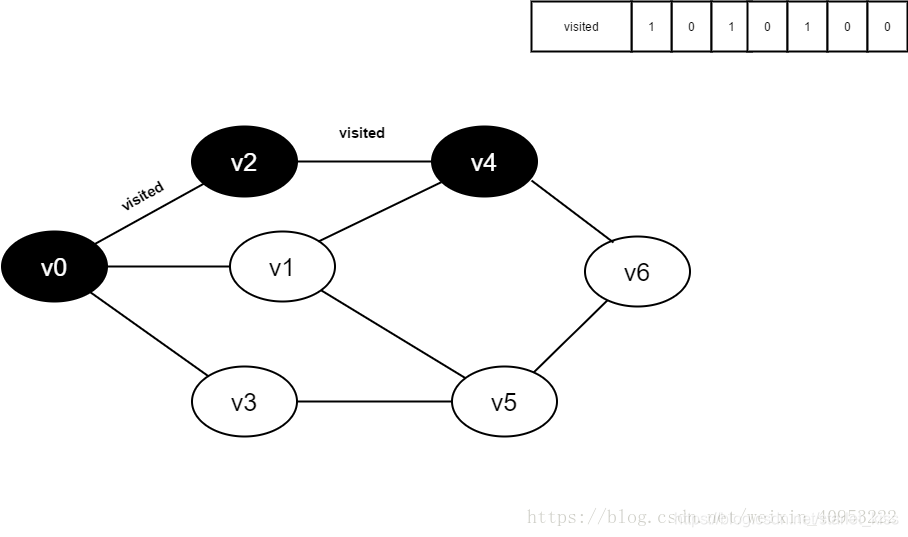
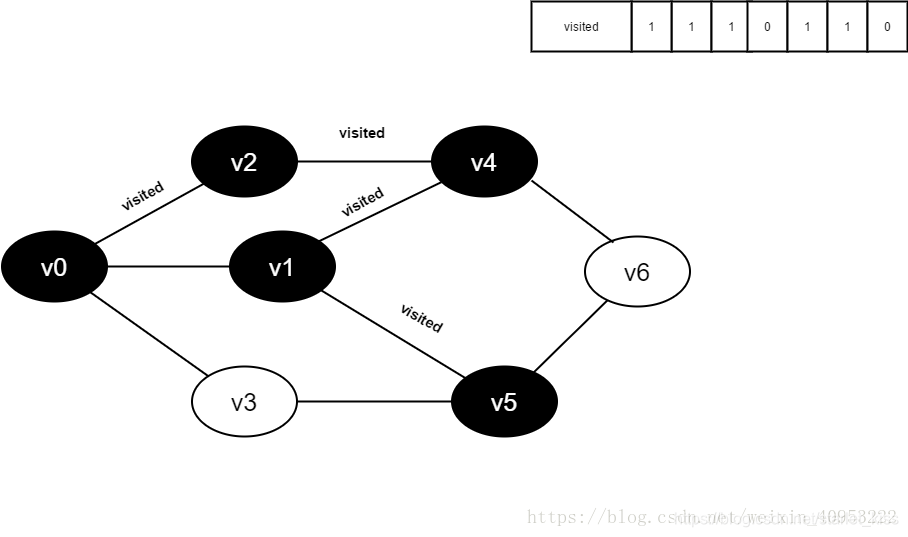
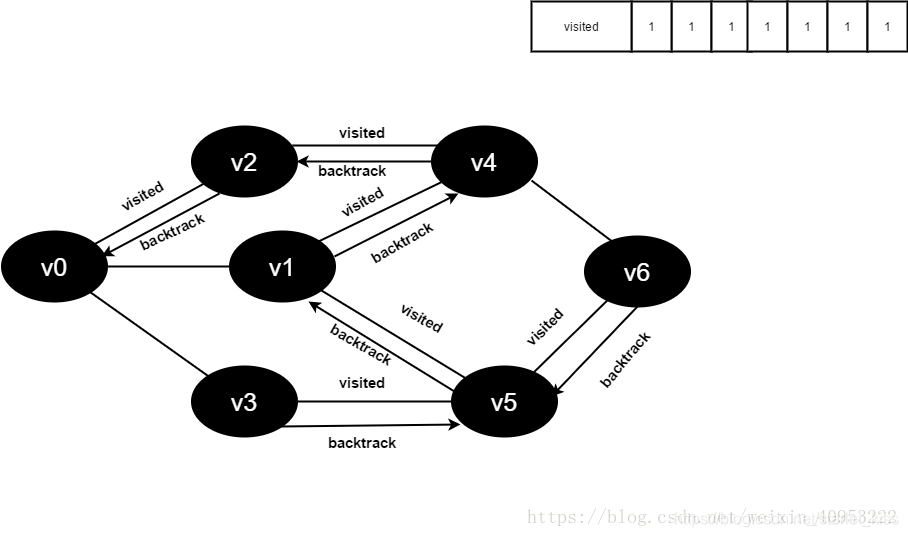
深度优先搜索如图所示：
1.初始时所有顶点均未被访问，visited数组为空。
在这里插入图片描述
2.即将访问v0。
在这里插入图片描述
3.访问v0，并将visited[0]的值置为1。
在这里插入图片描述
4.访问v0的邻接点v2，判断visited[2]，因其值为0，访问v2。
在这里插入图片描述
5.将visited[2]置为1。
在这里插入图片描述
6.访问v2的邻接点v0，判断visited[0]，其值为1，不访问。

继续访问v2的邻接点v4，判断visited[4]，其值为0，访问v4。
在这里插入图片描述
7.将visited[4]置为1。
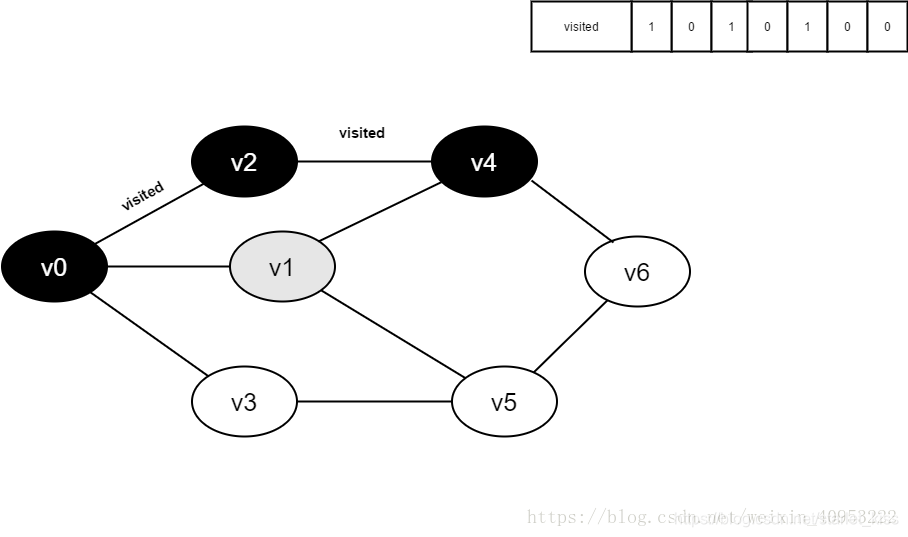
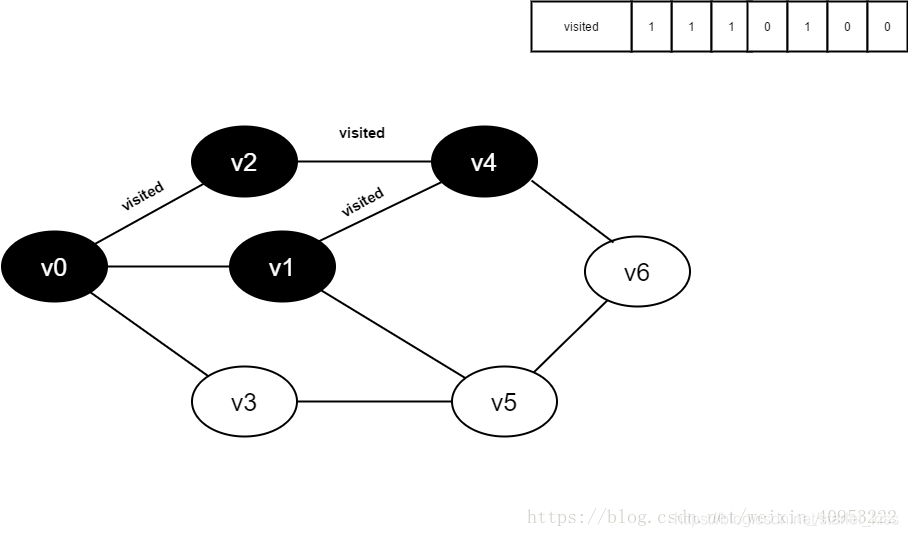
在这里插入图片描述
8.访问v4的邻接点v1，判断visited[1]，其值为0，访问v1。
在这里插入图片描述
9.将visited[1]置为1。
在这里插入图片描述
10.访问v1的邻接点v0，判断visited[0]，其值为1，不访问。

继续访问v1的邻接点v4，判断visited[4]，其值为1，不访问。

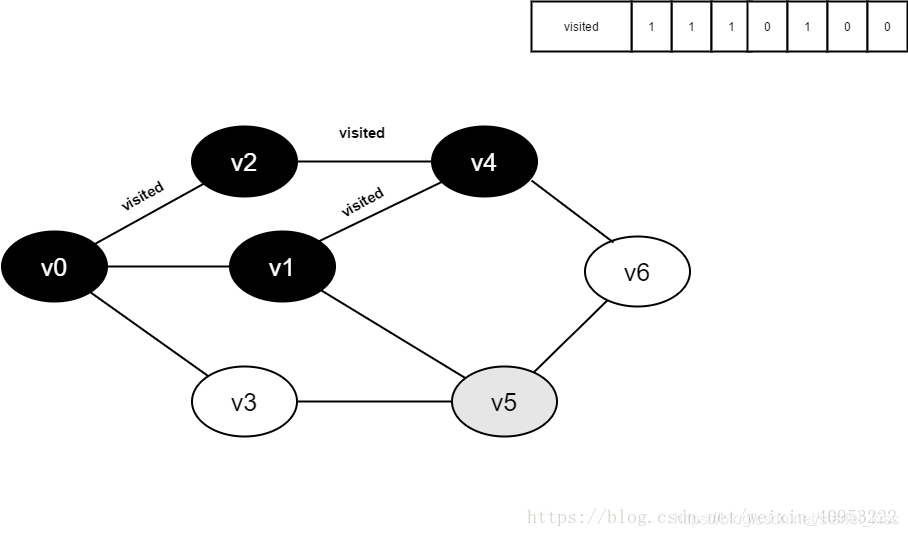
继续访问v1的邻接点v5，判读visited[5]，其值为0，访问v5。
在这里插入图片描述
11.将visited[5]置为1。
在这里插入图片描述
12.访问v5的邻接点v1，判断visited[1]，其值为1，不访问。

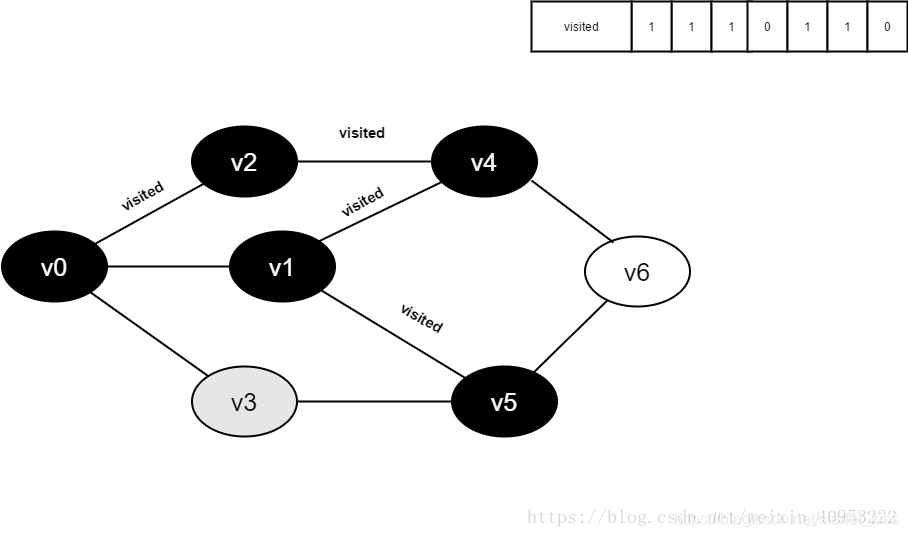
继续访问v5的邻接点v3，判断visited[3]，其值为0，访问v3。
在这里插入图片描述
13.将visited[1]置为1。
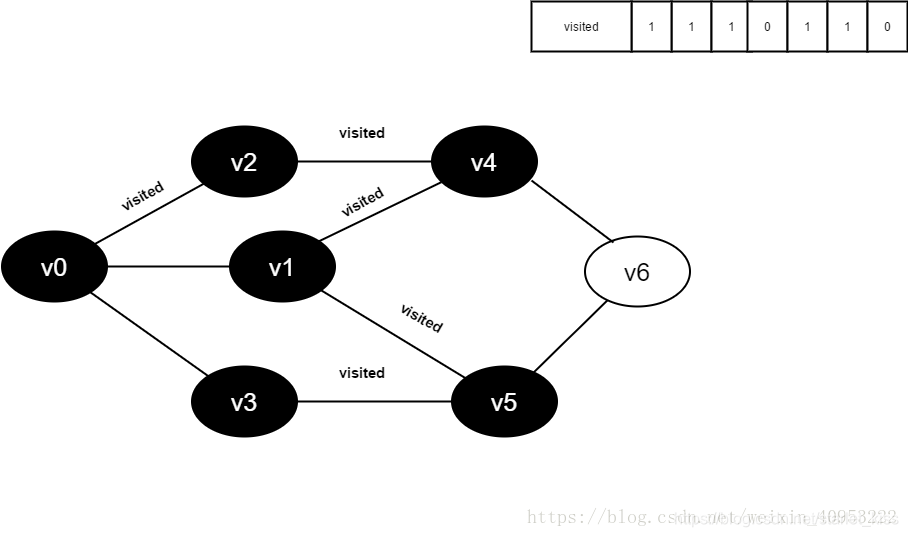
在这里插入图片描述
14.访问v3的邻接点v0，判断visited[0]，其值为1，不访问。

继续访问v3的邻接点v5，判断visited[5]，其值为1，不访问。

v3所有邻接点均已被访问，回溯到其上一个顶点v5，遍历v5所有邻接点。

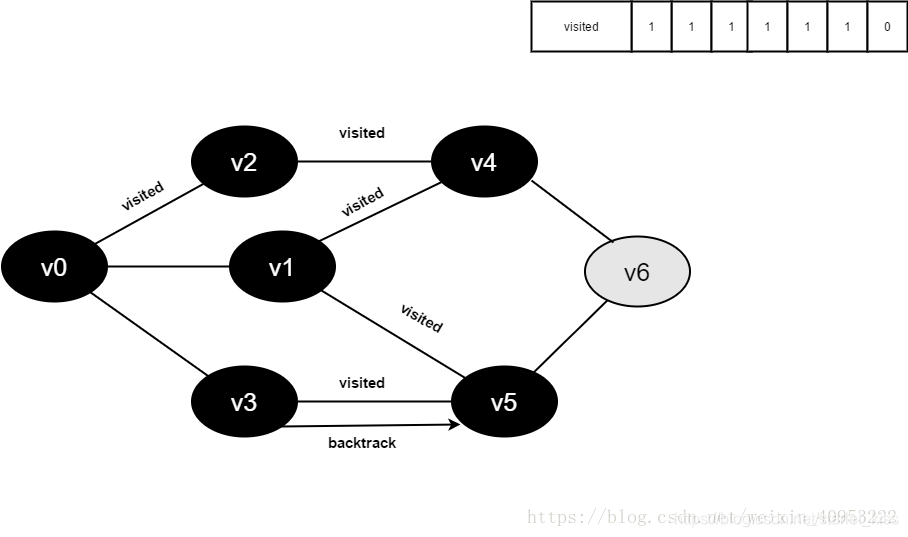
访问v5的邻接点v6，判断visited[6]，其值为0，访问v6。

在这里插入图片描述
15.将visited[6]置为1。
在这里插入图片描述
16.访问v6的邻接点v4，判断visited[4]，其值为1，不访问。

访问v6的邻接点v5，判断visited[5]，其值为1，不访问。

v6所有邻接点均已被访问，回溯到其上一个顶点v5，遍历v5剩余邻接点。
在这里插入图片描述
17.v5所有邻接点均已被访问，回溯到其上一个顶点v1。

v1所有邻接点均已被访问，回溯到其上一个顶点v4，遍历v4剩余邻接点v6。

v4所有邻接点均已被访问，回溯到其上一个顶点v2。

v2所有邻接点均已被访问，回溯到其上一个顶点v1，遍历v1剩余邻接点v3。

v1所有邻接点均已被访问，搜索结束。
在这里插入图片描述
深度优先搜索例题：
【例1】黑色方块

有一个宽为W、高为H的矩形平面，用黑色和红色两种颜色的方砖铺满。一个小朋友站在一块黑色方块上开始移动，规定移动方向有上、下、左、右四种，且只能在黑色方块上移动（即不能移到红色方块上）。编写一个程序，计算小朋友从起点出发可到达的所有黑色方砖的块数（包括起点）。

例如，如图1所示的矩形平面中，“#”表示红色砖块，“．”表示黑色砖块，“@”表示小朋友的起点，则小朋友能走到的黑色方砖有28块。
在这里插入图片描述
代码如下：

#include <iostream>
using namespace std;

#define N 21
struct Node
{
       int x;
       int y;
};
int dx[4]={-1,1,0,0};
int dy[4]={0,0,-1,1};
char map[N][N];
int visit[N][N];
int dfs(int startx, int starty,int w,int h)
{
       Node s[N*N],cur,next;     // s为栈
       int  top,i,x,y,sum;        // top为栈顶指针
       top=-1;                 // 栈S初始化
       sum=0;
       cur.x=startx;   cur.y=starty; 
       visit[startx][starty]=1;
       s[++top]=cur;           // 初始结点入栈；
       while(top>=0)           // 栈不为空
       {
              cur=s[top--];        // 栈顶元素出栈
              sum++;           // 方砖计数
              for (i=0;i<4;i++)
              {
                    x=cur.x+dx[i];  y=cur.y+dy[i];
                    if(x >=0 && x<h && y>=0 && y<w && map[x][y]!='#' && visit[x][y]==0)
                   {
                        visit[x][y] = 1;
                        next.x=x;  next.y=y;  // 由cur扩展出新结点next
                        s[++top]=next;        // next结点入栈
                    }
              }
       }
       return sum;
}

int main()
{
   int i,j,pos_x,pos_y,w,h,sum;
   while(1)
   {
          cin>>w>>h;
          if (w==0 && h==0) break;
          for(i=0;i<h;i++)
          {
              for(j=0;j<w;j++)
              {
                       cin>>map[i][j];
                        if (map[i][j]=='@')
                       {
                            pos_x = i;   pos_y = j;
                       }
                       visit[i][j] = 0;
                }
          }
          sum=dfs(pos_x, pos_y,w,h);
          cout<<sum<<endl;
   }
   return 0;
}

对于同样的问题，如果深搜和广搜都可以的话，推荐使用广搜，因为广搜不用递归调用系统栈，所以它的速度更快一些。
参考博客：
https://blog.csdn.net/weixin_40953222/article/details/80544928
https://www.cnblogs.com/cs-whut/p/11147213.html
努力加油a啊，(o)/~

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
【rCore OS 开源操作系统】Rust 智能指针
考虑源荷两侧不确定性的含风电电力系统低碳调度（Matlab代码实现）
EBM（基于能量的模型）
html CSS相关练习
springboot与ssm
原生DOM对象操作
关于对话框中放iframe ，内页高度问题
mysql里COALESCE_MySQL 技巧：COALESCE 函数的使用
二分查找算法(c++)
【LLM大模型】LangChain框架：Hub和LangSmith入门
;