第八课时：求解Ax=b：可解性和解的结构

本课时的目标是Ax=b，可能有解，也可能无解，需要通过需要消元才知道，有解的话是唯一解还是很多解。

1.Ax=b

首先，继续上次课的例子：

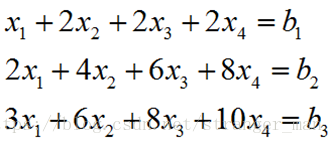
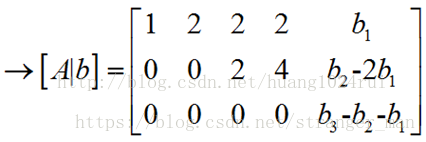
通过以上推导可以看到，如果方程组有解，必须满足$b_{3}=b_{1}+b_{2}$。消元告诉我们，这是必须的。换句话说，左侧行的线性组合得到0，那么右侧常量线性组合也比为0。

2、方程组Ax=b的可解性

从开头的例子可以看出，当Ax=b有解时，我们可以求出其解，其解的结构通常可以分为两部分：

特解
对方程的增广矩阵的消元，我们可以得到方程组的主元和自由变元，当我们将所有的自由元设定数值，并且利用自由变元求出主元，我们即可获得方程组的一个特解（因为我们对自由变元设定了值，所以我们称之为特定的解）。记为$x_{p}$。

通解（Null Space）
我们求解方程组$Ax=b$所对应的方程组$Ax=0$的解，即A的NullSpace（A的零空间）。记为$x_{n}$。

因此，$x_{p} + x_{n}$为方程组的解。（此解与$Ax = b$的解不在于同一个空间中）

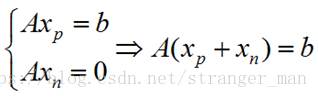
如在上面的例子中，其解是：

想象一下，$x_{p}$ 是一个非原点的点，$x_{n}$ 是一个穿过原点的平面，那么$x_{p}+x_{n}$ 是两者的组合，是一个不经过原点的经过$x_{p}$ 的二维平面，注意它不是子空间。

秩r与Ax = b的解的关系
对于一个m×n的矩阵A，他的秩r存在关系：r<=m,r<=n

列满秩，各列线性无关，即r=n：
每一列都有主元，0 个自由变量，此时零空间N(A)只有零向量，因为没有自由变量能够赋值，列的线性组合无法产生0 列（回顾下第六课时和第三课时，其中3 中讲到：如果存在非0 向量x，使的Ax=0，即x对A 的列向量的线性组合可以得到0 向量（有一列在线性组合中不起作用），那么A 是不可逆的。）。Ax=b 的全部解：0 个或唯一解，如果有解，即是唯一解特解$x_{p}$。

总结：

1.矩阵A 为m×n 的矩阵，Ax=b 的解的情况
2.r=m=n R=I 有唯一解b 是A 列向量的线性组合
3.r=m