题目

题目描述

给你一个满足下述两条属性的 m x n 整数矩阵：

每行中的整数从左到右按非严格递增顺序排列。
每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

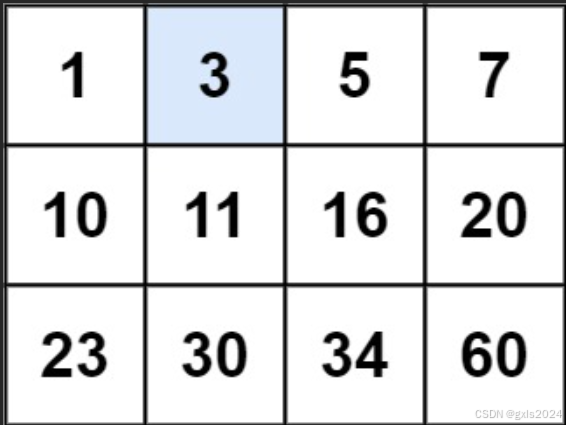
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-$10^4$ <= matrix[i][j], target <= $10^4$

题解

思路分析

由于矩阵具有每行和每列都是有序的特点，可以将二维矩阵视为一个一维的有序数组。因此，我们可以使用二分查找来高效地定位目标值。

二分查找算法步骤

1. 初始化边界：设定二分查找的左右边界 left 和 right。初始时，left 为 0，right 为 m * n - 1（其中 m 是矩阵的行数，n 是矩阵的列数）。
2. 计算中间位置：在每次迭代中，计算中间位置 mid，并将该位置映射回二维矩阵中的坐标 (row, col)。
3. 比较中间值与目标值：
   • 如果 matrix[row][col] == target，则找到了目标值，返回 true。
   • 如果 matrix[row][col] < target，则说明目标值位于右侧部分，更新 left。
   • 如果 matrix[row][col] > target，则说明目标值位于左侧部分，更新 right。
4. 循环结束条件：当 left 超过 right 时，说明没有找到目标值，返回 false。

Python 实现代码

def searchMatrix(matrix, target):
    if not matrix or not matrix[0]:
        return False
    
    m, n = len(matrix), len(matrix[0])
    left, right = 0, m * n - 1
    
    while left <= right:
        mid = (left + right) // 2
        mid_value = matrix[mid // n][mid % n]
        
        if mid_value == target:
            return True
        elif mid_value < target:
            left = mid + 1
        else:
            right = mid - 1
            
    return False

代码解释

1. 初始化边界：left 设置为 0，right 设置为 m * n - 1，表示整个矩阵的范围。
2. 计算中间位置：通过 mid = (left + right) // 2 计算中间位置，并将其转换为二维矩阵中的坐标 (mid // n, mid % n)。
3. 比较中间值与目标值：
   • 如果 matrix[mid // n][mid % n] == target，直接返回 true。
   • 如果 matrix[mid // n][mid % n] < target，说明目标值在右侧，更新 left。
   • 如果 matrix[mid // n][mid % n] > target，说明目标值在左侧，更新 right。
4. 循环结束条件：当 left 大于 right 时，说明遍历完整个矩阵仍未找到目标值，返回 false。

这种方法的时间复杂度为 O(log(m * n))，因为我们将二维矩阵视为一个一维的有序数组进行二分查找。空间复杂度为 O(1)，因为我们只使用了常数级别的额外空间。

提交结果