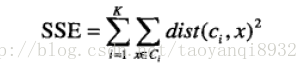概述

什么是聚类分析

聚类分析是在数据中发现数据对象之间的关系，将数据进行分组，组内的相似性越大，组间的差别越大，则聚类效果越好。

不同的簇类型

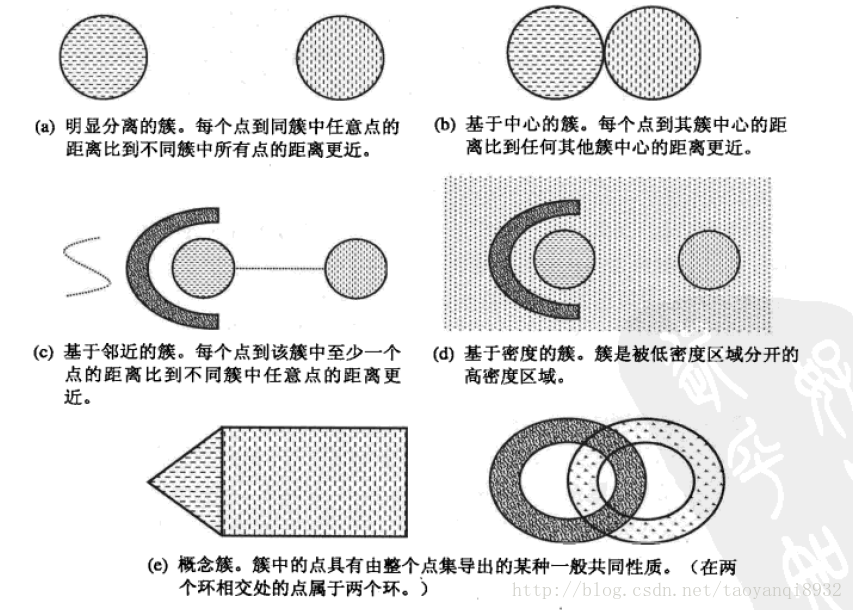
聚类旨在发现有用的对象簇，在现实中我们用到很多的簇的类型，使用不同的簇类型划分数据的结果是不同的，如下的几种簇类型。

明显分离的

可以看到(a)中不同组中任意两点之间的距离都大于组内任意两点之间的距离，明显分离的簇不一定是球形的，可以具有任意的形状。

基于原型的

簇是对象的集合，其中每个对象到定义该簇的原型的距离比其他簇的原型距离更近，如(b)所示的原型即为中心点，在一个簇中的数据到其中心点比到另一个簇的中心点更近。这是一种常见的基于中心的簇，最常用的K-Means就是这样的一种簇类型。
这样的簇趋向于球形。

基于密度的

簇是对象的密度区域，(d)所示的是基于密度的簇，当簇不规则或相互盘绕，并且有早上和离群点事，常常使用基于密度的簇定义。

关于更多的簇介绍参考《数据挖掘导论》。

基本的聚类分析算法

1. K均值：
基于原型的、划分的距离技术，它试图发现用户指定个数(K)的簇。

2. 凝聚的层次距离：
思想是开始时，每个点都作为一个单点簇，然后，重复的合并两个最靠近的簇，直到尝试单个、包含所有点的簇。

3. DBSCAN:
一种基于密度的划分距离的算法，簇的个数有算法自动的确定，低密度中的点被视为噪声而忽略，因此其不产生完全聚类。

距离量度

不同的距离量度会对距离的结果产生影响，常见的距离量度如下所示：

K-Means算法

下面介绍K均值算法：

优点：易于实现
缺点：可能收敛于局部最小值，在大规模数据收敛慢

算法思想较为简单如下所示：

选择K个点作为初始质心  
repeat  
    将每个点指派到最近的质心，形成K个簇  
    重新计算每个簇的质心  
until 簇不发生变化或达到最大迭代次数  

这里的重新计算每个簇的质心，如何计算的是根据目标函数得来的，因此在开始时我们要考虑距离度量和目标函数。

考虑欧几里得距离的数据，使用误差平方和（Sum of the Squared Error,SSE）作为聚类的目标函数，两次运行K均值产生的两个不同的簇集，我们更喜欢SSE最小的那个。

k表示k个聚类中心，ci表示第几个中心，dist表示的是欧几里得距离。
这里有一个问题就是为什么，我们更新质心是让所有的点的平均值，这里就是SSE所决定的。

下面用Python进行实现

# dataSet样本点,k 簇的个数
# disMeas距离量度，默认为欧几里得距离
# createCent,初始点的选取
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    m = shape(dataSet)[0] #样本数
    clusterAssment = mat(zeros((m,2))) #m*2的矩阵                   
    centroids = createCent(dataSet, k) #初始化k个中心
    clusterChanged = True             
    while clusterChanged:      #当聚类不再变化
        clusterChanged = False
        for i in range(m):
            minDist = inf; minIndex = -