【初阶数据结构】归并排序 - 分而治之的排序魔法

文章目录

前言
1. 什么是归并排序？
- 1.1 归并排序的步骤
2. 归并排序的代码实现
- 2.1 归并排序代码的关键部分讲解
3. 归并排序的非递归写法

前言

本文讲解的排序算法是归并排序，作为归并算法，其有着快速排序算法没有的特性，也是面试比较常考的算法之一。本文会重点讲解思路以及代码的实现。

OK，让我们来一场酣畅淋漓的排序冒险吧！！！

哈哈哈

1. 什么是归并排序？

归并排序（MergeSort）是一种基于分治法的高效排序算法，具有稳定性和较好的时间复杂度。归并排序的基本思想是将待排序数组递归地分成两个子数组，分别对这两个子数组进行排序，然后再将它们合并成一个有序数组。

我给大家看一下归并排序的动图：

1.1 归并排序的步骤

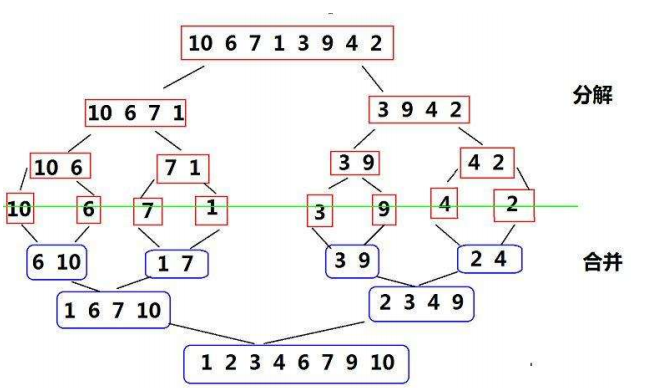
🍉分解：将数组从中间分为两部分，递归地对子数组进行相同的操作，直到子数组的长度为1（即每个子数组只有一个元素，天然有序）。
🍉合并：将两个有序的子数组合并成一个有序数组。合并的过程通过比较两个子数组的元素大小，按序依次放入目标数组。
🍉重复上述步骤，直到所有子数组都合并成一个有序数组。

也许你看到上面的步骤有点云里雾里的感觉，没有关系，下面我将给出一个具体的例子，带着大家，去理解上面的步骤。

🍇例子：假设我们要对数组 [3, 1, 4, 1, 5, 9, 2, 6] 进行归并排序：

将数组不断分成两部分，直到每个部分只有一个元素：
[3, 1, 4, 1, 5, 9, 2, 6]

分成 [3, 1, 4, 1] 和 [5, 9, 2, 6]

再分成 [3, 1] 和 [4, 1]，以及 [5, 9] 和 [2, 6]

继续分到每个部分只有一个元素：[3], [1], [4], [1], [5], [9], [2], [6]

合并有序子数组：

将 [3] 和 [1] 合并为 [1, 3]，将 [4] 和 [1] 合并为 [1, 4]

将 [5] 和 [9] 合并为 [5, 9]，将 [2] 和 [6] 合并为 [2, 6]

将 [1, 3] 和 [1, 4] 合并为 [1, 1, 3, 4]，将 [5, 9] 和 [2, 6] 合并为 [2, 5, 6, 9]

最后将 [1, 1, 3, 4] 和 [2, 5, 6, 9] 合并为 [1, 1, 2, 3, 4, 5, 6, 9]

最终得到有序数组 [1, 1, 2, 3, 4, 5, 6, 9]。

相信来看完上面的例子，你已经了解了归并排序的玩法了，那么接下来我们就得用代码来实现了。

2. 归并排序的代码实现

大家可以对照着这幅图来理解：

归并排序图片
可以看到归并排序的思想一定可以用递归来思想，接下来，我先给大家完整的代码，之后会对代码的关键部分讲解：

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
void _MergeSort(int* a, int left, int right, int* tmp)
{
	if (left >= right)
	{
		return;
	}

	int mid = (left + right) / 2;

	_MergeSort(a, left, mid, tmp);
	_MergeSort(a, mid + 1, right, tmp);


	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int i = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		if(a[begin1] >= a[begin2])
		{
			tmp[i++] = a[begin2++];
		}
	}

	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	memcpy(a + left, tmp + left, sizeof(int)*(right-left+1));
	
}


//归并排序
void MergeSort(int* a, int n)
{
	int left = 0, right = n - 1;
	int* tmp = (int*)malloc(n * sizeof(int));

	if (tmp == NULL) 
	{
		perror("malloc fail");
		return;
	}

	_MergeSort(a,left,right,tmp);	
}

这里我们采用的是用_MergeSort这个函数写归并排序的核心代码，这种写法的结构也是现在比较推崇的。

2.1 归并排序代码的关键部分讲解

为了让大家更好的吸收上述代码的思想，这里我将会详细的讲解代码关键部分的逻辑。
归并排序图片

2.1.1 利用递归

我们直到归并排序是采用分治思想的，其原理就是将一个数组拆解成一个一个有序的区间，最后经过比较合并之后才会称为一个有序的数组。那么，我们该如何，将数组拆成一个个区间呢？

利用递归就可以实现。有的人可能会问了，为什么会使用递归呢？

你可以这样想：我每次以数组中间位置的元素为界限，将数组拆分成两半。紧接着，又对已经拆分成两半的那两个数组再次进行这个操作。直至拆到没有元素或者是只剩一个元素为止，所以我们就可以推导出递归的条件为：左区间是否大于等于右区间。

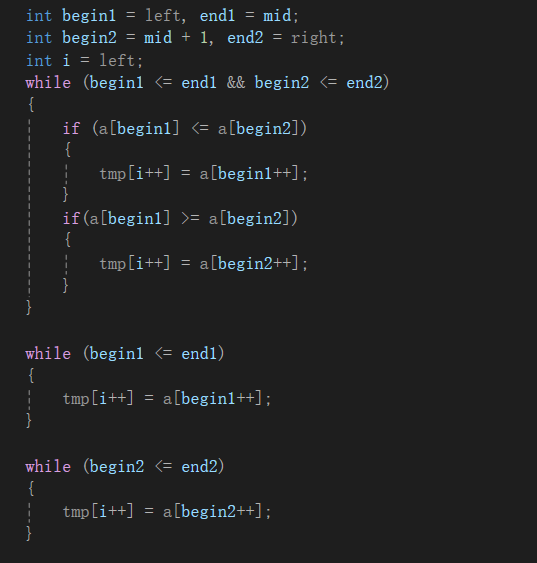
2.1.2 将拆解的数组的元素放到一个临时空间中进行重新排序

这段代码的作用：将拆解的数组的元素放到一个临时空间中进行重新排序。

有的人会问，那最后两个循环是怎么回事？

其实是这样的，你可以假设现在你有两个有序的数组，你要将这两个数组组成一个有序(升序)的数组，你会这么做：首先，你会分别拿出两个数组中的第一个元素互相比较，发现有其中一个元素的值比另一个要小，你就把那个小的元素的值放到一个你为一个有序(升序)的数组而申请的内存空间中，之后就拿下一个元素跟这个上次那个元素的值进行比较。
到后面，你会发现肯定有个数组里面的元素是没有被选中的，但是我们也不知道是哪一个，所以我们就可以都遍历一遍找到还没有被选中的元素，将它加进到你申请的空间中。

2.1.3 将在临时空间中排好的数组复制到目标数组中

这里你可以使用for循环，也可以用一个函数memcpy。这里我选择用后者。

当然，里面的参数十分的讲究。

解释：

a+left：这里不能直接写a。原因是，每一次拷贝会目标数组的位置不都是数组的头。
tmp+left：这里也不能直接写为tmp。原因是，每一次让待排序数组位置的元素进行排序时，我们要求位置得一一对应。

hahaha

3. 归并排序的非递归写法

非递归归并排序的主要步骤：

🍉初始化步长（子数组长度）为 1，这意味着开始时每个元素作为一个单独的有序数组。
🍉两两合并相邻的子数组，将步长长度的相邻子数组进行合并，形成更大的有序子数组。
🍉逐步增加步长，每次将步长翻倍，然后继续合并相邻的子数组，直到整个数组完全排序。

非递归归并排序的核心思想：归并排序的递归版从上到下拆分数组，而非递归版则从下到上逐步合并，模拟递归中“合并”的过程。在这个过程中，我们通过循环控制子数组的长度，每次将相邻的子数组合并成更大的有序数组。

具体步骤：

🍇从长度为 1 的子数组开始，对整个数组进行遍历，每两个相邻的子数组合并成一个长度为 2 的有序子数组。
🍇再次遍历时，将步长翻倍至 2，对整个数组中相邻的两个长度为 2 的有序子数组进行合并，形成长度为 4 的有序子数组。
🍇重复此过程，不断将步长翻倍（4, 8, 16，直到步长大于数组长度），直到整个数组有序。

由此，我们就可以通过上述思想，写出两个版本的代码：
版本1：

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;

	while (gap <= n / 2)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			//划分区间：[begin1,end1][begin2,end2]
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			//控制区间的边界
			if (end1 >= n)
			{
				end1 = n - 1;
				begin2 = n;
				end2 = n - 1;
			}
			else if (begin2 >= n)
			{
				begin2 = n;
				end2 = n - 1;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}

			int j = i;

			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a+i, tmp+i, sizeof(int) * (end2-i+1));


		}

		memcpy(a, tmp, sizeof(int) * n);

		gap *= 2;
	}

	free(tmp);
	tmp = NULL;
}

版本2：

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;

	while (gap <= n / 2)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			//划分区间：[begin1,end1][begin2,end2]
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			
			
			int j = i;

			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a+i, tmp+i, sizeof(int) * (end2-i+1));

		}
		gap *= 2;
	}

	free(tmp);
	tmp = NULL;
}

好了，到这里归并排序的内容就已经全部讲完了。如果大家觉得本文写的还不错的话。麻烦给偶点个赞吧！！！

哈哈哈