文本识别论文之Aster解读
一、Aster解读—Level1 梳理论文思路
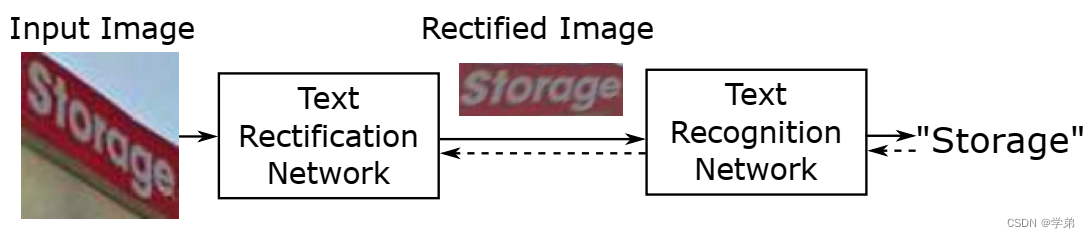
ASTER是独立于另一篇博文CTC文本识别的另一篇经典识别论文。它的全称是A ttentional S cene Te xt Recognizer with Flexible R ectification。
首先作者找到了一个值得研究的学术问题:在自然场景下,存在扭曲文字和非常规布局的现象,讲的再数学性一点就是透视变换和曲形文字,单纯的文本识别器对该情形的识别能力有限。
- 速度慢
- opencv是在求一个闭式解,无法智能的学习、推理
识别网络,作者采用了Attentional 识别模型,这算是有别于CTC方案目前介绍的第二文本识别流派。
再来看一看,校正前后的图片效果,效果可能不够完美,但应该讲都还是有朝着好的方向发展。
二、Aster解读—Level2 理解论文数学原理
2.1 尝试对TPS的数学原理进行理解
TPS算法求解通用图像转换的思想是将其转换为一个最优化问题。提出了以下假设:
- 寻找到的转换方式,尽可能得“拟合”已知的控制点。
- 寻找到的转换方式,使得原始图像拟合控制点的“扭曲度”尽可能的小。
这有点类似于一些小学找规律题目。
1----3-----5-----7------(?)
找出其中的规律,并补充括号中的数字
按照TPS的思想,找到的规律为y=2*x-1, 括号中的答案为9。因为寻找到的规律(尽可能)满足了原始提供的4个控制点(1,3,5,7), 且规律足够的简单(对应扭曲度足够小)。之所以强调规律足够简单,是因为如果较真的话,我们也可以设计出一个复杂的规律,使得其前4个数字也满足{1, 3, 5,7},但注意到此时已经不满足“扭曲度”尽可能小的思想。
因此TPS最优化的问题可以描述为:
ε
=
ε
t
+
λ
ε
d
\varepsilon=\varepsilon_t + \lambda\varepsilon_{d}
ε=εt+λεd。前面一项称之为拟合项,后面一项称之为扭曲度。通过求上述等式的最小值,可以求得tps算法闭式解的形式为:
T
(
c
)
=
m
0
+
M
∗
c
+
∑
i
=
1
K
ω
i
ϕ
(
∣
∣
c
−
c
i
∣
∣
)
T(c)= m_{0} + M*c + \sum_{i=1}^{K}\omega_{i}\phi(||c-c_{i}||)
T(c)=m0+M∗c+∑i=1Kωiϕ(∣∣c−ci∣∣)。
这也是Aster这篇论文中transformation矩阵表示形式的由来。
T
2
∗
(
K
+
3
)
=
[
a
0
a
1
a
2
u
1
∗
k
b
0
b
1
b
2
v
1
∗
k
]
T_{2*(K+3)}=\left[ \begin{matrix} a_{0} & a_{1} & a_{2} & u_{1*k}\\ b_{0} & b_{1} & b_{2} & v_{1*k} \end{matrix} \right]
T2∗(K+3)=[a0b0a1b1a2b2u1∗kv1∗k]
根据一个控制点,我们可以获得两个等式(因为一个点有x和y两个维度):
p
2
∗
1
′
=
T
[
1
p
ϕ
(
∣
∣
p
−
c
1
∣
∣
)
.
.
.
ϕ
(
∣
∣
p
−
c
K
∣
∣
)
]
p^{'}_{2*1} = T\left[ \begin{matrix} 1\\ p\\ \phi(||p-c_{1}||)\\ ...\\ \phi(||p-c_{K}||) \end{matrix} \right]
p2∗1′=T
1pϕ(∣∣p−c1∣∣)...ϕ(∣∣p−cK∣∣)
类推我们已知
K
K
K个控制点,所以我们可以得到
2
∗
K
2*K
2∗K个等式:
C
2
∗
K
′
=
T
2
∗
(
K
+
3
)
[
1
1
.
.
.
1
c
0
c
1
.
.
.
c
K
−
1
ϕ
(
∣
∣
c
0
−
c
0
∣
∣
)
ϕ
(
∣
∣
c
1
−
c
0
∣
∣
)
.
.
.
ϕ
(
∣
∣
c
K
−
1
−
c
0
∣
∣
)
.
.
.
.
.
.
.
.
.
.
.
.
ϕ
(
∣
∣
c
0
−
c
K
−
1
∣
∣
)
ϕ
(
∣
∣
c
1
−
c
K
−
1
∣
∣
)
.
.
.
ϕ
(
∣
∣
c
K
−
1
−
c
K
−
1
∣
∣
)
]
C^{'}_{2*K}=T_{2*(K+3)}\left[ \begin{matrix} 1 & 1 & ... & 1\\ c_{0} & c_{1} & ... & c_{K-1}\\ \phi(||c_{0}-c_{0}||) & \phi(||c_{1}-c_{0}||) & ... & \phi(||c_{K-1}-c_{0}||)\\ ... & ... & ... & ...\\ \phi(||c_{0}-c_{K-1}||) & \phi(||c_{1}-c_{K-1}||) & ... & \phi(||c_{K-1}-c_{K-1}||) \end{matrix} \right]
C2∗K′=T2∗(K+3)
1c0ϕ(∣∣c0−c0∣∣)...ϕ(∣∣c0−cK−1∣∣)1c1ϕ(∣∣c1−c0∣∣)...ϕ(∣∣c1−cK−1∣∣)...............1cK−1ϕ(∣∣cK−1−c0∣∣)...ϕ(∣∣cK−1−cK−1∣∣)
但要知道的是
T
T
T含有
2
∗
(
K
+
3
)
2*(K+3)
2∗(K+3)个参数, 但我们目前仅仅有
2
K
2K
2K个等式方程,这是无法求解到的,因此作者人为添加了6个约束:
0
=
u
∗
1
0=u*1
0=u∗1
0
=
v
∗
1
0=v*1
0=v∗1
0
=
u
∗
c
x
T
0=u*c^{T}_{x}
0=u∗cxT
0
=
v
∗
c
y
T
0 = v*c^{T}_{y}
0=v∗cyT
0
=
u
∗
c
y
T
−
−
A
s
t
e
r
论文中没有,我感觉是作者写漏了
0 = u * c^{T}_{y}--Aster论文中没有,我感觉是作者写漏了
0=u∗cyT−−Aster论文中没有,我感觉是作者写漏了
0
=
v
∗
c
x
T
−
−
A
s
t
e
r
论文中没有,我感觉是作者写漏了
0 = v * c^{T}_{x}--Aster论文中没有,我感觉是作者写漏了
0=v∗cxT−−Aster论文中没有,我感觉是作者写漏了
有了这6个等式,我们可以"padding"得到如下的
2
∗
(
K
+
3
)
2*(K+3)
2∗(K+3)个等式:
C
2
∗
K
′
,
[
0
0
0
0
0
0
]
=
T
2
∗
(
K
+
3
)
[
1
1
.
.
.
1
0
0
c
0
c
1
.
.
.
c
K
−
1
0
0
ϕ
(
∣
∣
c
0
−
c
0
∣
∣
)
ϕ
(
∣
∣
c
1
−
c
0
∣
∣
)
.
.
.
ϕ
(
∣
∣
c
K
−
1
−
c
0
∣
∣
)
1
c
0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
ϕ
(
∣
∣
c
0
−
c
K
−
1
∣
∣
)
ϕ
(
∣
∣
c
1
−
c
K
−
1
∣
∣
)
.
.
.
ϕ
(
∣
∣
c
K
−
1
−
c
K
−
1
∣
∣
)
1
C
K
−
1
]
C^{'}_{2*K},\left[ \begin{matrix} 0 & 0 & 0\\ 0 & 0 & 0\end{matrix}\right]=T_{2*(K+3)}\left[ \begin{matrix} 1 & 1 & ... & 1 & 0 & 0\\ c_{0} & c_{1} & ... & c_{K-1} & 0 & 0\\ \phi(||c_{0}-c_{0}||) & \phi(||c_{1}-c_{0}||) & ... & \phi(||c_{K-1}-c_{0}||) & 1 & c_{0}\\ ... & ... & ... & ... & ... & ...\\ \phi(||c_{0}-c_{K-1}||) & \phi(||c_{1}-c_{K-1}||) & ... & \phi(||c_{K-1}-c_{K-1}||) & 1 & C_{K-1} \end{matrix} \right]
C2∗K′,[000000]=T2∗(K+3)
1c0ϕ(∣∣c0−c0∣∣)...ϕ(∣∣c0−cK−1∣∣)1c1ϕ(∣∣c1−c0∣∣)...ϕ(∣∣c1−cK−1∣∣)...............1cK−1ϕ(∣∣cK−1−c0∣∣)...ϕ(∣∣cK−1−cK−1∣∣)001...100c0...CK−1
这也就是论文中Aster中如下写法的由来:
T
∇
C
=
[
C
′
0
2
∗
3
]
T\nabla_{C} = \left[ \begin{matrix} C^{'} & 0^{2*3} \end{matrix} \right]
T∇C=[C′02∗3]
∇
C
=
[
1
1
∗
K
0
0
C
0
0
C
^
1
K
∗
1
C
T
]
\nabla_{C} = \left[ \begin{matrix} 1^{1*K} & 0 & 0 \\C & 0 & 0\\ \widehat{C} & 1^{K*1} & C^{T} \end{matrix}\right]
∇C=
11∗KCC
001K∗100CT
我们想要求得得转换
T
T
T, 则可以表示为:
T
=
[
C
′
0
2
∗
3
]
∗
∇
C
−
1
T = \left[ \begin{matrix} C^{'} & 0^{2*3} \end{matrix} \right] * \nabla_{C}^{-1}
T=[C′02∗3]∗∇C−1
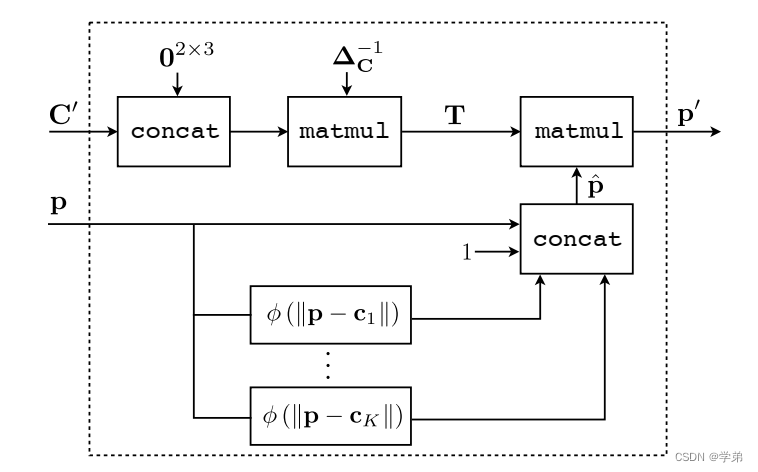
作者用上图来模拟了TPS过程,
C
′
C_{'}
C′是STN网络中的localization网络预测得到的控制点。并根据规则确定出了输出控制点
C
C
C, 规则按照论文上的说法为,细节这边还需要再看一下代码。
at fixed locations along the top and bottom image borders with equal spacings
有了输出图片上 p p p对应的输入图片上 p ′ p_{'} p′之后(这一步对应STN网络的grid_generator),就可以进一步利用STN模块上的Sampler模块,获得校正后的图片。STN也在这篇博文中进行了解读,如果对localization、grid_generator和sampler三子模块不熟悉的可以跳转查看。
三、Aster解读—Level3 通过Attentional 避开CTC loss
在CTC LOSS这篇文章中介绍了由于图片块中字体大小以及布局之间的关系,具体的,例如说,如果图片中S这个字母特别大,可能会导致出现SSSTATE这样的“结巴现象”, 但通过后处理操作可以将其修正为STATE。通过CTC Loss可以巧妙的计算出所有情形的概率。而Aster这篇论文使用了Attentional的方式就可以避免上述的问题,从而避开CTC Loss。
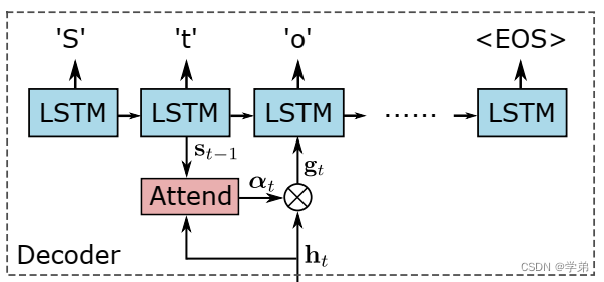
论文中也绘制了基于Attentional的Sequence-to-Sequence模型的简图:
如下的计算权重以及加权的公式更加直观明显:
e
t
,
i
=
w
T
t
a
n
h
(
W
s
t
−
1
+
V
h
i
+
b
)
e_{t,i} = w^Ttanh(W_{s_{t-1}} + Vh_{i} + b)
et,i=wTtanh(Wst−1+Vhi+b)
α
t
,
i
=
e
x
p
(
e
t
,
i
)
/
∑
i
′
=
1
n
e
x
p
(
e
t
,
i
′
)
\alpha_{t,i} = exp(e_{t,i})/ \sum_{i^{'}=1}^{n} exp(e_{t,i^{'}})
αt,i=exp(et,i)/∑i′=1nexp(et,i′)
g
t
=
∑
i
=
1
n
α
t
,
i
h
i
g_t=\sum_{i=1}^{n}\alpha_{t,i}h_{i}
gt=∑i=1nαt,ihi
四、Aster解读—Level4 思考
思考:
- tps+x应该是一种可以推广的方式,端到端的,无需额外标签。
- tps中有6个等式是默认其等于0来获得2K+6个方程组。是否可以将其设置为等于V, 而V是可学习的,从而获得更优的解。