智能优化算法应用:基于鹈鹕算法的二维Otsu图像阈值分割
摘要:1维Otsu法根据1维直方图来确定分割阈值,由于未考虑像素点邻域平均灰度值导致确定的分割阈值不准确,造成图像分割不正确,因研究人员提出了一种2维Otsu分割法。结合鹈鹕寻优能够得到较好的分割结果。
1.二维Otsu算法原理
2维Otsu法是在1维Otsu法的基础上引入像素点的邻域均值,原理如下 :假设原图像
f
(
x
,
y
)
f(x,y)
f(x,y)和经过均值滤波(滤波窗口为 3× 3 )后的图像
g
(
x
,
y
)
g(x,y)
g(x,y) 的灰度级总数都为
L
L
L,所有像素点的像素和为
N
N
N,那么可以用二元数组
(
i
,
j
)
(i,j)
(i,j)来描述图像中的任意像素点,其中i和j分别是像素灰度值和邻域平均灰度值。假设在图像中像素点
(
i
,
j
)
(i,j)
(i,j) 存在的个数为
N
i
j
N_{ij}
Nij ,则该像素点出现的概率为:
P
i
j
=
N
i
j
/
N
,
∑
i
=
0
L
−
1
∑
j
=
0
L
−
1
p
i
j
=
1
(1)
P_{ij}=N_{ij}/N,\sum_{i=0}^{L-1}\sum_{j=0}^{L-1}p_{ij}=1\tag{1}
Pij=Nij/N,i=0∑L−1j=0∑L−1pij=1(1)
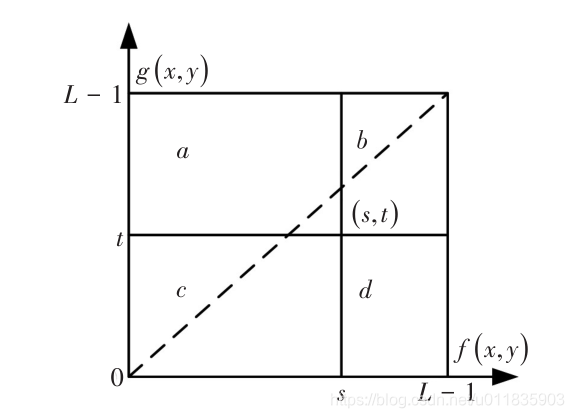
随机给定一个分割阈值数组
(
s
,
t
)
(s,t)
(s,t),可将图像分为如图1所示的4个部分。图1中a、b、c、d依次表示图像中的边界、背景、目标和噪声。设该分割阈值将图像划分出的背景类
C
0
C_0
C0 和目标类
C
1
C_1
C1 出现的概率分别为
w
0
w_0
w0 和
w
1
w_1
w1 ,即:
w
0
=
∑
i
=
0
s
−
1
∑
j
=
0
t
−
1
p
i
j
(2)
w_0=\sum_{i=0}^{s-1}\sum_{j=0}^{t-1}p_{ij}\tag{2}
w0=i=0∑s−1j=0∑t−1pij(2)
w 1 = ∑ i = s s − 1 ∑ j = t t − 1 p i j (3) w_1=\sum_{i=s}^{s-1}\sum_{j=t}^{t-1}p_{ij}\tag{3} w1=i=s∑s−1j=t∑t−1pij(3)
则背景
C
0
C_0
C0和目标
C
1
C_1
C1区域对应的均值矢量为:
u
0
=
(
u
0
i
,
u
o
j
)
T
=
[
∑
i
=
0
s
−
1
∑
j
=
0
t
−
1
i
p
i
j
,
∑
i
=
0
s
−
1
∑
j
=
0
t
−
1
j
p
i
j
]
T
(4)
u_0=(u_{0i},u_{oj})^T=[\sum_{i=0}^{s-1}\sum_{j=0}^{t-1}ip_{ij},\sum_{i=0}^{s-1}\sum_{j=0}^{t-1}jp_{ij}]^T\tag{4}
u0=(u0i,uoj)T=[i=0∑s−1j=0∑t−1ipij,i=0∑s−1j=0∑t−1jpij]T(4)
u 1 = ( u 1 i , u 1 j ) T = [ ∑ i = s L − 1 ∑ j = t L − 1 i p i j , ∑ i = 0 s − 1 ∑ j = 0 t − 1 j p i j ] T (5) u_1=(u_{1i},u_{1j})^T=[\sum_{i=s}^{L-1}\sum_{j=t}^{L-1}ip_{ij},\sum_{i=0}^{s-1}\sum_{j=0}^{t-1}jp_{ij}]^T\tag{5} u1=(u1i,u1j)T=[i=s∑L−1j=t∑L−1ipij,i=0∑s−1j=0∑t−1jpij]T(5)
则总的均值矢量为:
u
=
(
u
1
i
,
u
j
)
T
=
[
∑
i
=
0
L
−
1
∑
j
=
0
L
−
1
i
p
i
j
,
∑
i
=
0
L
−
1
∑
j
=
0
L
−
1
j
p
i
j
]
T
(6)
u=(u_{1i},u_{j})^T=[\sum_{i=0}^{L-1}\sum_{j=0}^{L-1}ip_{ij},\sum_{i=0}^{L-1}\sum_{j=0}^{L-1}jp_{ij}]^T\tag{6}
u=(u1i,uj)T=[i=0∑L−1j=0∑L−1ipij,i=0∑L−1j=0∑L−1jpij]T(6)
其类间离散矩阵定义如下:
Q
(
s
,
t
)
=
w
0
(
u
0
−
u
)
2
+
w
1
(
u
1
−
u
)
2
(7)
Q(s,t)=w_0(u_0-u)^2+w_1(u_1-u)^2\tag{7}
Q(s,t)=w0(u0−u)2+w1(u1−u)2(7)
将离散矩阵的迹作为
C
0
C_0
C0 区域和
C
1
C_1
C1 区域的类间离散度测度,即:
R
t
r
a
c
e
(
Q
(
s
,
t
)
)
=
(
w
0
+
w
1
)
∗
[
(
u
0
i
−
u
i
)
2
+
(
u
o
j
−
u
j
)
2
]
(8)
R_{trace}(Q(s,t))=(w_0+w_1)*[(u_{0i}-u_i)^2+(u_{oj}-u_j)^2]\tag{8}
Rtrace(Q(s,t))=(w0+w1)∗[(u0i−ui)2+(uoj−uj)2](8)
当
R
t
r
a
c
e
(
Q
(
s
,
t
)
)
R_{trace}(Q(s,t))
Rtrace(Q(s,t))取最大值时,此时确定的分割阈值
(
s
0
,
t
0
)
(s_0,t_0)
(s0,t0)是最优的,则目标可以较好地被分割出来,即:
R
t
r
a
c
e
(
Q
(
s
0
,
t
0
)
)
=
m
a
x
(
R
t
r
a
c
e
(
Q
(
s
,
t
)
)
)
,
0
≤
s
≤
L
−
1
,
0
≤
t
≤
L
−
1
(9)
R_{trace}(Q(s_0,t_0)) = max(R_{trace}(Q(s,t))),0\leq s\leq L-1,0\leq t \leq L-1 \tag{9}
Rtrace(Q(s0,t0))=max(Rtrace(Q(s,t))),0≤s≤L−1,0≤t≤L−1(9)
2.基于鹈鹕优化的二维otsu阈值分割
由上述二维Otsu阈值分割法的原理可知,要得到最终的阈值,需要去寻找阈值(s,t),使得离散度测度最大。于是可以利用智能优化算法进行阈值的寻优,使得获得最佳阈值。
于是优化的适应度函数就是:
f
u
n
{
T
1
∗
,
T
2
∗
,
.
.
.
,
T
n
−
1
∗
}
=
m
a
x
(
R
t
r
a
c
e
(
Q
(
s
,
t
)
)
)
,
0
≤
s
≤
L
−
1
,
0
≤
t
≤
L
−
1
fun\{T_1^*,T_2^*,...,T_{n-1}^*\} =max(R_{trace}(Q(s,t))),0\leq s\leq L-1,0\leq t \leq L-1
fun{T1∗,T2∗,...,Tn−1∗}=max(Rtrace(Q(s,t))),0≤s≤L−1,0≤t≤L−1
设置阈值分割的个数,寻优边界为0到255(因为直方图的灰度级范围为0-255),设置相应的鹈鹕算法参数
鹈鹕算法原理请参考:https://blog.csdn.net/u011835903/article/details/124809854
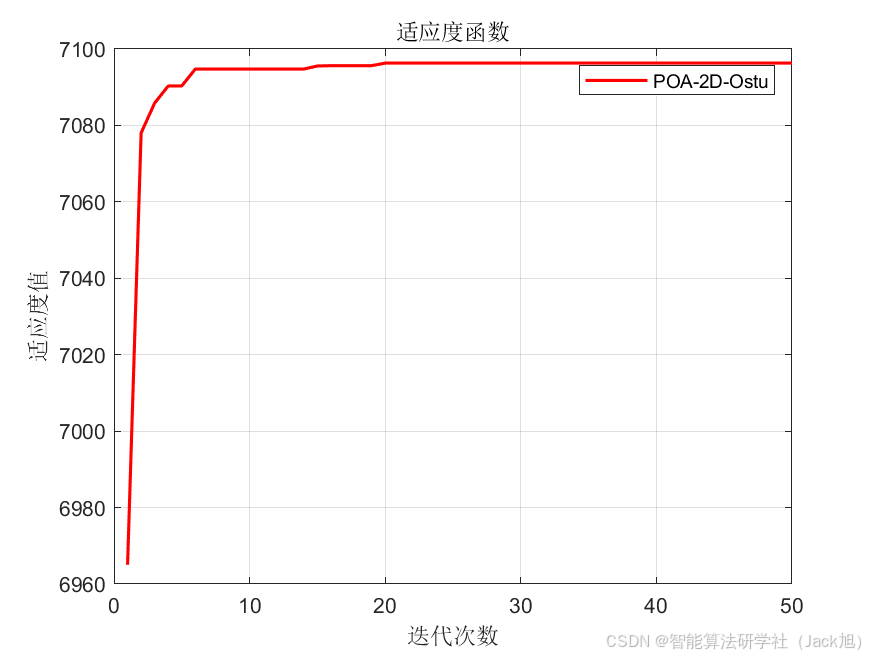
3.算法结果
4.参考文献
[1]邵闯,王生怀,邹春龙,周红勋.基于混合粒子群优化的2维Otsu路面裂缝图像阈值分割方法[J].湖北汽车工业学院学报,2019,33(03):53-57.