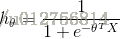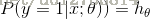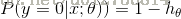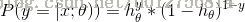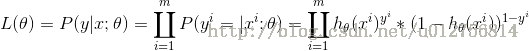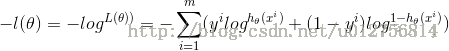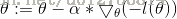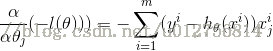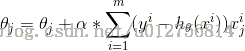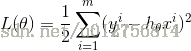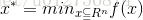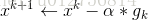本文尝试对吴恩达深度学习工程师课程中的第一部分神经网络与深度学习做一些总结，并添加一些其他相关知识。主要目的是为了更清晰的梳理学习脉络和一些细节。作为尚未入行的小白，文章可能有各种各样的错误和问题，希望各位能批评指正。
本文主要包括以下几部分：
1、logistic 回归 
2、什么是神经网络，神经网络到底实现了什么？
3、为什么一定要深？
4、梯度下降，链式法则，反向传播算法 和计算图
5、向量化
6、对课程中反向传播过程出现的矩阵转置做一个简单的阐述。
7、常见的激活函数以及为什么要使用非线性激活函数
8、使用python搭建深度神经网络

1、logistic 回归：
本节第一部分对logistic 回归进行了推导，并给出优化算法；
第二部分详细解释了为什么logistic 回归 cost函数使用交叉熵，而不是最小二乘。
logistic 回归数学推导：
logistic 回归虽然名为回归，但其实是一种分类算法，这种算法有很多优点，可以直接对分类的可能性进行建模，无需事先假设数据分布，因此，相比于其他分类算法，例如GDA（高斯判别分析，高斯假设），Naive Bayes（朴素贝叶斯，条件独立假设）等算法，避免了假设分布不准确所带来的问题，有更好的鲁棒性。

而且，它不仅预测出类别，还可以近似得到概率预测，这对许多辅助决策的任务很有用。也可以推广为多元分类模型，即softmax模型。

logisitc 模型如下：

为需要学习的参数

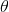
总结上式得到：

最大似然有：

取对数有：

最大化似然函数，等价于最小化负的似然函数，因此，cost函数为：

利用梯度下降法可知：

具体的关于cost函数的推导过程比较长，限于时间，就不在这里详细论述，具体可参见吴恩达斯坦福机器学习课程附材料，这里只说明大概思路，sigmoid函数的导数 a(1-a),cost
函数中存在log(a)与log(1-a)，求导后，a和1-a会到分母上，根据链式法则，两者相乘，经过化简，可以得到如下公式：

从而可实现对参数的更新：

为什么cost函数是交叉熵而不是最小二乘：

事实上 linear regression ，logistic regression 还有其他一些算法都可以从 可以看作广义线性模型（GLM）推导而来，（这里只做说明，不做推导，具体可参见吴恩达斯坦福机器学习课程附材料，）只需要决定y的分布，
例如，假设y 属于高斯分布

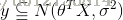
就可以推导出，最大化似然函数就等价于最小二乘。

同理假设y属于伯努利分布，就可以推导出logistic regression，通过最大似然推导出cost为交叉熵。

上面的方法，从理论上说明了，为什么logistic使用交叉熵，而不是最小二乘，但是还不够直观，接下来给出一种更加易于理解的思路：
假设损失函数为最小二乘，即，

求导可得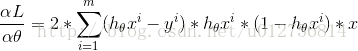： （注：（sigmoid函数的导数是a(1-a)））
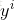
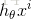
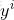
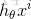
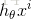
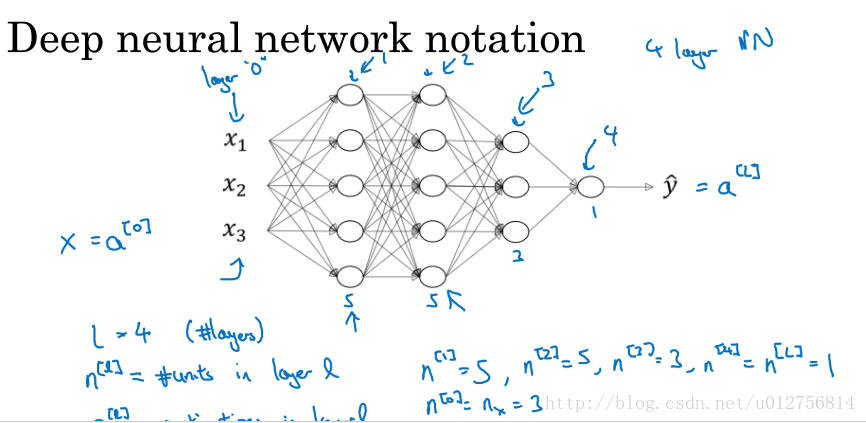
分析上式，假设 等于1，而 等于0，此时目标与预测值之间有很大误差，但是导数为0，无法实现优化，同理当 等于0，等于1，1- 等于0，那么loss函数也等于0。

2、什么是神经网络

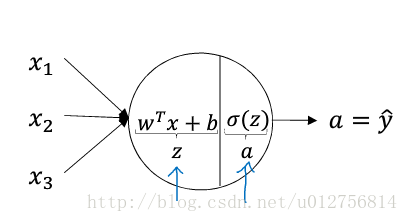
上边两张图说明了神经网络的基本结构，图1为单个神经元模型，输入层加权叠加，加上偏置值，然后经过激活函数，进行输出，可以作为下一层的输入或最终的输出，图2是一个4层深度神经网络（输入为第0层，不计入层数），图中每个圆圈代表一个神经元（每一个连接代表一个需要学习的权值，偏置项没有显示在图中。可以想象在每一层的输入都有一个值为1的项指向下一层的每个神经元。偏置项也需要学习得到），给定一个网络结构，实际上就是给定了一个假设空间。

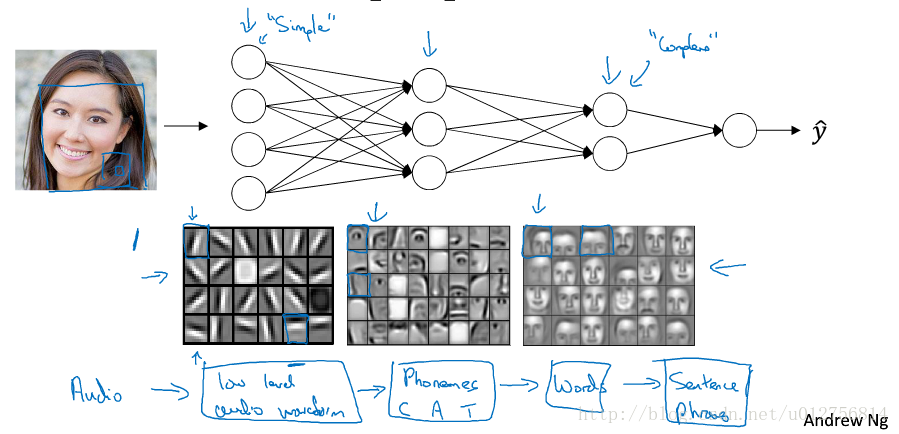
神经网络到底实现了什么？

当我们将一个训练好的神经网络训练好之后，输入一个data，然后将每一层的结果，进行输出，可以明显看到，每一个隐藏层都像一个特征抽取器，一层一层的由简及繁抽取资料的模式，并将这些模式作为更高级的特征，然后将这些更高级的特征交给输出层，使用相对简单的函数，即可实现分类或者其他任务。常规机器算法都需要人为设计特征，但特征工程非常重要但又难设计，也是制约人工智能发展的瓶颈（例如语音识别和图像识别特征难以设计，因此深度学习优势非常明显，但NLP领域特征，相对容易抽取，因此优势并不是十分明显）。

神经网络将问题从如何抽取特征转变为如何设计网络结构的问题。但是网络结构的设计也是一个非常开放的问题，需要设计多少隐藏层，每一层需要多少个神经元，没有定论，只能通过通过不断的试验和直觉，经验，硬件条件等。另外，神经元之间的连接方式也是一个开放的问题，比较经典的模型包括卷积神经网络，循环神经网络，递归神经网络等等。

3、为什么一定要深？

上一节内容说明了，神经网络将特征抽取问题转变为网络架构的问题，本节尝试说明一下，为什么一定要深。我认为可以总结为如下两个原因：1、参数耦合 2、问题解耦，下面就这两方面进行一些论述：

虽然我们处于一个大数据时代，但仍然面临着数据不充分的问题，尤其是带有标记的数据，因此，如何有效的避免overfitting 仍然是一个非常重要的问题，事实上上文关于为什么一定要深的总结，都是为了减弱overfitting影响。
许多人认为，深度神经网络，参数量巨大，因此容易overfitting，事实上，参数量巨大，是因为我们面对的问题太过复杂，必须用大量的参数进行描述，相比于常规的机器学习算法（例如决策树，HMM，矩阵分解等），深度神经网络所需要的参数要少的多，事实上更不容易overfitting（会在以后的文章中进行论述）。

假设采用相同的神经元数目（相同的参数量），宽胖的模型，参数之间的相关性差，而瘦高（deep）模型，参数之间相互耦合，因此有更丰富的表达能力，因此瘦高模型使用比较少的参数，即可实现复杂的模型，有效减少overfitting的影响。

deep 神经网络将一个大问题逐层分解为一个个小问题，使问题逐渐解耦，而分解后的每个小问题，只需要少量的数据，即可训练好，因此需要更少的数据，减少overfitting的影响。

4、梯度下降，链式法则，反向传播算法 和计算图

梯度下降法：

梯度下降法（gradient descent）是求解无约束最优化问题的一种最常用方法，是实现神经网络训练（反向传播）的基础。

假设f(x)是具有一阶连续偏导数的函数(实际应用中并不十分严格，比如relu函数)，最优化的问题可以表示为：

梯度下降法是一种迭代算法，选取适当的初值，不断迭代，更新参数值，进行目标函数的最小化，直到收敛，负梯度方向是使函数值下降最快的方向，在迭代的每一步，以负梯度方向更新参数的值，从而达到最小化参数值的目的。

f(x)具有一阶连续导数，若第k次迭代值为$x^k$ ,根据一阶泰勒展开将f(x)在$x^k$ 处展开，有如下公式：$f(x)=f(x^k) + g_k(x-x^k)$,这里$g_k$为f(x)在$x^k$处的梯度，通过迭代可以得到：

当目标函数为凸函数时，梯度下降法的解释全局最优解(比如logistic regression)，但一般情况下，其解不保证是全局最优解，而且梯度下降法的收敛速度也未必很快，但是深度神经网络训练过程，反向传播采用梯度下降算法，因此本文只简要说明梯度下降。

链式法则：

在论述链式法则之前，先做一些符号上的说明，
假设网络有L层，
第l层的神经元个数为$d^l$
第l层,第i个神经元的线性加权值为$z_i^l$,经过激活函数后的输出值为$a_i^l$，
第l-1层第i个元素，连接到第l层第j个元素的权值为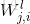
第l-1层到第l层第j个元素的偏置值为$b_j^l$
假设 a0i=