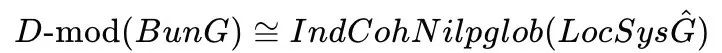9 位数学家、横跨 30 余年、5 篇论文共计 800 + 页…… 中国学者陈麟系主要作者

1967 年，年仅 30 岁的加拿大数学家罗伯特・朗兰兹在给美国数学家安德烈・韦伊的一封信中，提出了一组意义深远的猜想。这些猜想指出了三个相对独立发展起来的数学分支：数论、代数几何和群表示论，实际上它们是密切相关的。
这些猜想现在被称为朗兰兹互反猜想，而后演变成朗兰兹纲领，被称为数学界的 “大统一理论”，在过去几十年里对数学的发展产生了极大影响。

几何朗兰兹猜想，终于被证明！

它是朗兰兹纲领的几何化版本。

朗兰兹纲领被视为现代数学研究中最大的单项项目，被称为 “数学的大统一理论”。它提出数论、代数几何、群表示论这三个独立发展的数学分支之间其实密切相关。

费马大定理被完全证明，就得益于对朗兰兹纲领的应用。安德鲁・威尔斯（Andrew Wiles）对一小部分函数的数论朗兰兹的关系的证明，就解决了困扰数学界 300 年的难题。

几何朗兰兹猜想作为朗兰兹纲领的几何版本，在上世纪 80 年代被提出。它提供了一种将数论方法和概念应用于几何问题（反之亦成立）的框架。

利用该猜想，可以为数学、物理领域诸多悬而未决的问题提供新思路和工具。比如可以应用于量子场论和弦理论研究。

因此，当几何朗兰兹猜想被证明，无疑会轰动数学界。

主要研究朗兰兹纲领的菲尔兹奖得主彼得・舒尔茨（Peter Scholze）将这一最新成果评价为 “30 年努力的巅峰”。

看到它能被解决真的太好了！

几何朗兰兹纲领创始人之一亚历山大・贝林森（Alexander Beilinson）也表示：

这个证明真的非常美丽，是同类中最好的。

该研究由丹尼斯・盖茨戈里（Dennis Gaitsgory）和山姆・拉斯金（Sam Raskin）领导完成。

9 人团队中，还包括中国学者陈麟。

他是清华大学丘成桐数学科学中心助理教授，曾在 15 岁时摘得 IMO 金牌。

几何，朗兰兹纲领的最后一环

朗兰兹纲领的提出在 1967 年。

30 岁的普林斯顿大学教授罗伯特・朗兰兹（Robert Langlands）给 “数学的罗塞塔石碑” 创始人安德烈・韦尔 (André Weil) 寄去了一封长达 17 页的手写信，信中向阐述了他的愿景。

（这里的 “罗塞塔石碑” 是一种比喻，指的是由数学家 André Weil 提出的一个数学领域之间的类比，这个类比把数论、几何学和函数域这三个看似不同的数学领域联系在了一起。）

朗兰兹写道，在 “罗塞塔石碑” 的数论和函数域中，有可能创建出傅里叶分析的推广。

傅里叶分析是一种将复杂波形表示为平滑振荡三角函数波的框架，是现代电信、信号处理、磁共振成像以及许多现代生活的基本技术。

类似于傅里叶分析中函数与其傅里叶变换之间的关系，朗兰兹纲领通过在这三个领域中建立类似的 “对应关系” 将它们联系起来。

傅里叶变换在波和频谱之间来回转换，朗兰兹纲领当中也有相应的 “波” 和 “频谱”。

其中 “波” 的一面由某些特殊函数构成，“频谱” 的一面则由某些代数对象构成，用以标记 “波” 的频率：

• 在数论中，函数是定义在 p-adic 数域或者阿德尔环上的特殊函数，代数对象是 Galois 群或者与之相关的群的表示；
• 在几何中，函数是定义在黎曼曲面上的特征层 (D - 模)，代数对象是黎曼曲面基本群在某个代数群 G 上的表示；
• 在函数域中，函数是定义在曲线上的特殊函数，代数对象是 Galois 群或者与之相关的群的表示。

因此，朗兰兹纲领提供了一个统一的视角，将数论、几何、函数域这三个数学分支联系起来，并由此带来了一系列深刻而广泛的数学问题和猜想。

通过朗兰兹纲领的框架，许多传统数论中的难题可以转化为表示论或其他领域中的问题，从而以新的视角和工具加以解决，朗兰兹纲领的思想和方法在许多具体的数学问题中得到了应用。

△罗伯特・朗兰兹

例如，费马大定理的证明就借鉴了朗兰兹纲领中的思想，将椭圆曲线和模形式联系起来，并最终通过这些联系取得了成功。

除了数学本身，朗兰兹纲领对物理学等其他学科也起到了重要作用，比如在量子场论和弦理论中，朗兰兹纲领的某些思想和方法得到了应用。

其中，几何朗兰兹猜想不仅拥有更广泛的应用和联系，还提供了几何视角的强大工具，因此在朗兰兹纲领中显得尤为重要。

但几何朗兰兹猜想证明的历程也十分艰难，前后一共跨越了跨越 30 年，最终的证明工作从 2013 年才开始。

核心的证明内容，是关于黎曼曲面上的自相似性和对称性的深层次对应关系。

再次借用傅里叶分析的模式来解释的话，就是数学家们很早就了解了几何朗兰兹猜想的 “频谱” 一侧，但对 “波” 一侧的理解则经历了漫长的过程。

甚至在朗兰兹刚提出这一纲领的时候，几何部分根本没有被包括在内，直到 80 年代，数学家弗拉基米尔・德林费尔德（Vladimir Drinfeld）意识到，通过用特征层替换特征函数，有可能创建一个几何版本的朗兰兹对应关系。

而几何朗兰兹猜想的精确表述，更是本世纪才出现 ——2012 年，丹尼斯・盖茨戈里（Dennis Gaitsgory）与迪玛・阿林金（Dima Arinkin）一起，用一篇 150 多页的论文给出了这一表述。

丹尼斯和阿林金指出，证明几何朗兰兹猜想的核心思想是找到一个等价关系，将代数曲线 X 上的 G - 丛（代数空间 G 上的纤维丛，其纤维是 G 的副本）的 D - 模（某些空间上的微分方程的解）范畴与朗兰兹对偶群𝐺^ 的局部系统的 Ind-Coh 范畴（包含了所有 Ind - 上同调对象）联系起来，即：

2013 年，丹尼斯写下了几何朗兰兹猜想证明的草图，但这个草图依赖于许多尚未被证明的中间结果，此后的几年，丹尼斯和他的合作者致力于证明这些结果。

2020 年，丹尼斯开始思考如何理解每个特征层对 “白噪声” 的贡献，这一思想后来成为证明的关键部分。

这里的 “白噪声” 指的是结合朗兰兹猜想中的庞加莱层（Poincaré sheaf），作者以此类比是基于傅里叶变换中的正弦波。

2022 年春，山姆・拉斯金（Sam Raskin）和他的学生乔阿基姆・费尔格曼（Joakim Færgeman）证明了每个特征层都以某种方式贡献于 “白噪声”，这一结果让丹尼斯确信他们很快就能完成证明。

从 2023 年起， 丹尼斯、山姆以及其他 7 位合作者向几何朗兰兹猜想发起了最后攻关，最终的证明包含 5 篇论文，篇幅超过 800 页，并于今年发表。

第一篇关于函子（functor）的构造，需要在特征为零的环境下，从自守（automorphic）到谱方向构造几何朗兰兹函子 LG 并证明其等价性，即能够在两个范畴之间建立一一对应的关系。

如果这一等价性能够得到证明，那么就能说明几何朗兰兹猜想成立。

第二篇研究了 Kac-Moody 定位与全局的相互作用，证明了该函子在特定条件下确实是一个等价性函子，从而推进了几何朗兰兹猜想的证明。

第三篇起到了桥梁的作用，不仅将已知的等价性结果扩展到了更一般的情况，而且还通过 Kac-Moody 局部化技术，为理解几何朗兰兹函子与常数项函子的兼容性提供了关键的洞见。

同时，通过证明在可约谱参数下几何朗兰兹猜想的兼容性，这一篇论文为进一步证明不可约谱参数下的几何朗兰兹猜想奠定了基础。

在第四篇论文中，作者们证明了一个关键的定理 ——Ambidexterity 定理。这个定理表明，LG-cusp（可以视为 LG 在一个特定的、更小的范畴上的行为）的左伴随和右伴随是同构的，这是证明 LG 是一个等价性函子的重要步骤。

最后一篇论文则利用这一结论将猜想推广到了一般情况，为旷日持久的证明工作画上了句号。

两代数学家合力攻坚

研究团队由哈佛大学教授丹尼斯・盖茨戈里（Dennis Gaitsgory）和耶鲁大学教授山姆・拉斯金（Sam Raskin）领衔。

其余作者从左至右顺时针方向分别是：达里奥・贝拉尔多（Dario Beraldo）、陈麟（Lin Chen）、凯文・林（Kevin Lin）、尼克・罗森布吕姆（Nick Rozenblyum）、乔阿基姆・费尔格曼（Joakim Færgeman）、贾斯廷・坎贝尔（Justin Campbell）和迪玛・阿林金（Dima Arinkin）。

△图源：Quantamagazine

值得关注的是，研究小组包括中国学者：陈麟。

陈麟，清华大学丘成桐数学科学中心助理教授。2016 在北京大学取得学士学位，2021 年博士毕业于哈佛大学，曾荣获哈佛 2020-2021 优秀奖学金。

他曾在十几岁时就展现出超强的数学天赋，12 岁进入中国数学奥林匹克（CMO）竞赛并获得满分，15 岁进入国家队并参加国际数学奥林匹克（IMO）竞赛取得金牌。

陈麟长期研究几何朗兰兹纲领，他与该方向的结缘，正是来自丹尼斯・盖茨戈里。

陈麟在此前采访中透露，他是在丹尼斯的带领下才进入几何朗兰兹这一领域。博士之前，他几乎对几何表示论一无所知，很多基础知识都是在丹尼斯的指导下学习的。

博士毕业后，陈麟也一直参与丹尼斯和其他合作者的研究项目，有关全局的范畴化几何朗兰兹猜想。

完成猜想证明以及论文撰写后，他还会继续思考关于局部几何朗兰兹的问题。

实际上，朗兰兹纲领吸引着诸多中国数学学者。北大黄金一代中的恽之玮、张伟、袁新意、朱歆文，也正在攀登这一高峰。

参考链接：
https://www.quantamagazine.org/monumental-proof-settles-geometric-langlands-conjecture-20240719/
http://www.mathchina.com/bbs/forum.php?mod=viewthread&tid=2060061

—完—

via：

• 几何朗兰兹猜想被解决！历时 30 年、证明论文达 800 余页，中国学者陈麟系主要作者 明敏 克雷西 发自 凹非寺 量子位 2024 年 07 月 23 日 17:59 北京

  https://mp.weixin.qq.com/s/CXXYP8AMtp_YB_j_GsomvQ

注： 机翻，未校对。

具有历史意义的证明解决了几何 Langlands 猜想

Monumental Proof Settles Geometric Langlands Conjecture

In work that has been 30 years in the making, mathematicians have proved a major part of a profound mathematical vision called the Langlands program.

Read Later

Nan Cao for Quanta Magazine

By Erica Klarreich

Contributing Correspondent
特约通讯员

July 19, 2024 7 月 19， 2024

Introduction 介绍

A group of nine mathematicians has proved the geometric Langlands conjecture, a key component of one of the most sweeping paradigms in modern mathematics.
由九位数学家组成的小组证明了几何朗兰兹猜想，这是现代数学中最广泛的范式之一的关键组成部分。

The proof represents the culmination of three decades of effort, said Peter Scholze, a prominent mathematician at the Max Planck Institute for Mathematics who was not involved in the proof. “It’s wonderful to see it resolved.”
马克斯・普朗克数学研究所（Max Planck Institute for Mathematics）的著名数学家彼得・舒尔茨（Peter Scholze）说，这个证明代表了三十年努力的顶峰，他没有参与证明。“很高兴看到它得到解决。”

The Langlands program, originated by Robert Langlands in the 1960s, is a vast generalization of Fourier analysis, a far-reaching framework in which complex waves are expressed in terms of smoothly oscillating sine waves. The Langlands program holds sway in three separate areas of mathematics: number theory, geometry and something called function fields. These three settings are connected by a web of analogies commonly called mathematics’ Rosetta stone.
Langlands 程序由 Robert Langlands 于 1960 年代发起，是对傅里叶分析的广泛推广，傅里叶分析是一个影响深远的框架，其中复杂波以平滑振荡的正弦波表示。Langlands 程序在数学的三个独立领域占据主导地位：数论，几何和称为函数场的东西。这三个设置通过一个类比网络连接起来，通常被称为数学的罗塞塔石碑。

Now, a new set of papers has settled the Langlands conjecture in the geometric column of the Rosetta stone. “In none of the [other] settings has a result as comprehensive and as powerful been proved,” said David Ben-Zvi of the University of Texas, Austin.
现在，一组新的论文已经确定了罗塞塔石碑几何柱中的朗兰兹猜想。“在 [其他] 环境中，没有一个结果得到如此全面和有力的证明，” 德克萨斯大学奥斯汀分校的 David Ben-Zvi 说。

“It is beautiful mathematics, the best of its kind,” said Alexander Beilinson, one of the main progenitors of the geometric version of the Langlands program.
“这是美丽的数学，是同类中最好的，” 亚历山大・贝林森（Alexander Beilinson）说，他是 Langlands 程序几何版本的主要祖先之一。

The proof involves more than 800 pages spread over five papers. It was written by a team led by Dennis Gaitsgory (Scholze’s colleague at the Max Planck Institute) and Sam Raskin of Yale University.
校样涉及 800 多页，分布在五篇论文中。它是由丹尼斯・盖茨戈里（朔尔茨在马克斯・普朗克研究所的同事）和耶鲁大学的山姆・拉斯金领导的团队撰写的。

Gaitsgory has dedicated the past 30 years to proving the geometric Langlands conjecture. Over the decades, he and his collaborators have developed a massive body of work on which the new proof rests. Vincent Lafforgue, of Grenoble Alps University, likened these advances to a “rising sea,” in the spirit of the preeminent 20th-century mathematician Alexander Grothendieck, who spoke of tackling hard problems by creating a gradually rising sea of ideas around them.
在过去的 30 年里，Gaitsgory 一直致力于证明几何朗兰兹猜想。几十年来，他和他的合作者已经开展了大量的工作，新的证明就建立在这些工作之上。格勒诺布尔阿尔卑斯大学的文森特・拉福格（Vincent Lafforgue）本着 20 世纪杰出的数学家亚历山大・格罗滕迪克（Alexander Grothendieck）的精神，将这些进步比作 “上升的海”，他谈到通过在它们周围创造一个逐渐上升的思想海洋来解决难题。

Newsletter

Get Quanta Magazine delivered to your inbox

Recent newsletters

Dennis Gaitsgory (left) and Sam Raskin led the nine-person team that proved the geometric Langlands conjecture.
丹尼斯・盖茨戈里（左）和山姆・拉斯金（Sam Raskin）领导的九人团队证明了几何朗兰兹猜想。

From left: Natasha Bershadsky; Charlotte Krontiris
左起：娜塔莎・贝尔沙德斯基；夏洛特・克朗蒂里斯

Introduction 介绍

It will take mathematicians a while to digest the new work, but many have expressed confidence that the core ideas are correct. “The theory has a lot of internal consistencies, so it’s difficult to believe there could be a mistake,” Lafforgue said.
数学家需要一段时间来消化这些新工作，但许多人表示相信核心思想是正确的。“这个理论有很多内部一致性，所以很难相信会有一个错误，” 拉夫福格说。

In the years leading up to the proof, the research team created not one but many routes into the heart of the problem, Ben-Zvi said. “The understanding that they’ve developed is so rich and so broad, they’ve encircled the problem from every direction,” he said. “It had no way to escape.”
Ben-Zvi 说，在证明之前的几年里，研究团队创造了一条不是一条而是多条进入问题核心的途径。“他们已经形成的理解如此丰富和广泛，他们已经从各个方向包围了这个问题，” 他说。“它没有办法逃脱。”

A Grand Unified Theory 大一统理论

In 1967, Robert Langlands, then a 30-year-old professor at Princeton University, laid out his vision in a handwritten 17-page letter to André Weil, the originator of the Rosetta stone. Langlands wrote that in the number theory and function field columns of the Rosetta stone, it might be possible to create a generalization of Fourier analysis with startling scope and power.
1967 年，时年 30 岁的普林斯顿大学教授罗伯特・朗兰兹（Robert Langlands）在一封长达 17 页的手写信中阐述了他的愿景，信中是罗塞塔石碑的创始人。Langlands 写道，在罗塞塔石碑的数论和函数场列中，有可能以惊人的范围和功效创建傅里叶分析的推广。

number theory

A Rosetta Stone for Mathematics
数学用的罗塞塔石碑

May 6, 2024

Read Later

In classical Fourier analysis, a procedure called the Fourier transform creates a correspondence between two different ways of thinking about the graph of a wave (such as a sound wave). On one side of the correspondence are the waves themselves. (We’ll call this the wave side.) These include both simple sine waves (which in acoustics are pure tones) and more complicated waves that are combinations of sine waves. On the other side of the correspondence is the spectrum of frequencies of the sine waves — that is, their pitches. (Mathematicians call this the spectral side.)
在经典的傅里叶分析中，一种称为傅里叶变换的过程在两种不同的思考波形图（如声波）的方式之间创建了对应关系。对应关系的一侧是波浪本身。（我们称之为波浪侧。它们既包括简单的正弦波（在声学中是纯音调），也包括更复杂的正弦波（正弦波的组合）。对应关系的另一面是正弦波的频率谱，即它们的音高。（数学家称其为光谱侧。

The Fourier transform goes back and forth between these two sides. In one direction, it allows you to break down a wave into a collection of frequencies; in the other, it allows you to reconstruct the wave from its constituent frequencies. The ability to move across this divide is central to a wide range of applications — without it, we wouldn’t have modern telecommunications, or signal processing, or magnetic resonance imaging, or numerous other essentials of modern life.
傅里叶变换在这两边之间来回切换。在一个方向上，它允许您将波分解为频率集合；另一方面，它允许您从其组成频率重建波。跨越这一鸿沟的能力对于广泛的应用至关重要 —— 没有它，我们就不会有现代电信、信号处理、磁共振成像或现代生活的许多其他必需品。

Langlands proposed that something similar occurs in the number theory and function field columns of the Rosetta stone, but with more complicated waves and frequencies.
Langlands 提出，在罗塞塔石的数论和函数场柱中也发生了类似的事情，但波和频率更复杂。

Video: Rutgers University mathematician Alex Kontorovich takes us on a journey through the continents of mathematics to learn about the awe-inspiring symmetries at the heart of the Langlands program.
视频：罗格斯大学数学家亚历克斯・康托罗维奇（Alex Kontorovich）带领我们穿越数学大陆，了解朗兰兹计划核心的令人敬畏的对称性。

Emily Buder / Quanta Magazine; Adrian Vasquez de Velasco, Björn Öberg, Rui Braz, and Guan-Huei Wu for Quanta Magazine

Introduction 介绍

In each of these columns separately, there is a wave side that consists of a collection of special functions analogous to repeating waves. The purest of these, which are called eigenfunctions (from the German for “characteristic”), play the role of sine waves. Each eigenfunction has a characteristic frequency. But whereas the frequency of a sine wave is a single number, the frequency of an eigenfunction is an infinite list of numbers.
在这些列中的每一列中，都有一个波侧，该波侧由类似于重复波的特殊函数集合组成。其中最纯粹的称为特征函数（来自德语的 “特性”），起着正弦波的作用。每个特征函数都有一个特征频率。但是，正弦波的频率是一个单一的数字，而特征函数的频率是一个无限的数字列表。

There’s also a spectral side. This consists of a collection of objects from number theory that, Langlands argued, label the spectrum of frequencies of the eigenfunctions. A procedure akin to the Fourier transform, he proposed, connects the wave side and the spectral side. “That’s kind of a miraculous thing,” Ben-Zvi said. “It’s not something, a priori, we had any reason to expect.”
还有一个光谱方面。Langlands 认为，它由数论中的一组对象组成，这些对象标记了特征函数的频率谱。他提出了一种类似于傅里叶变换的程序，将波侧和光谱侧连接起来。“这是一件神奇的事情，”Ben-Zvi 说。“这不是先验的事情，我们有任何理由期待。”

The waves and their frequency labels come from widely disparate realms of mathematics, so the correspondence between them — when it can be proved — often comes with bountiful rewards. For instance, a proof of the number theory Langlands correspondence for a comparatively small collection of functions in the 1990s enabled Andrew Wiles and Richard Taylor to prove Fermat’s Last Theorem, which for three centuries had been one of the most famous open questions in mathematics.
波及其频率标签来自截然不同的数学领域，因此它们之间的对应关系 —— 如果可以证明的话 —— 往往会带来丰厚的回报。例如，在 1990 年代，数论 Langlands 对应关系的证明使 Andrew Wiles 和 Richard Taylor 能够证明费马大定理，该定理在三个世纪以来一直是数学中最著名的开放性问题之一。

Langlands’ program came to be seen, in the words of Edward Frenkel of the University of California, Berkeley, as a “grand unified theory of mathematics.” Yet even as mathematicians turned their efforts to proving larger and larger pieces of Langlands’ vision, they were aware that this vision was incomplete. It didn’t seem to be able to tell a story of waves and their frequency labels in the third column of the Rosetta stone — the geometry portion.
用加州大学伯克利分校（University of California， Berkeley）的爱德华・弗伦克尔（Edward Frenkel）的话来说，朗兰兹的程序被看作是 “数学的大统一理论”。然而，即使数学家们将精力转向证明朗兰兹的视野越来越大的部分，他们也意识到这个愿景是不完整的。它似乎无法讲述罗塞塔石碑第三列（几何部分）中波及其频率标签的故事。

A Grain of Sand 一粒沙子

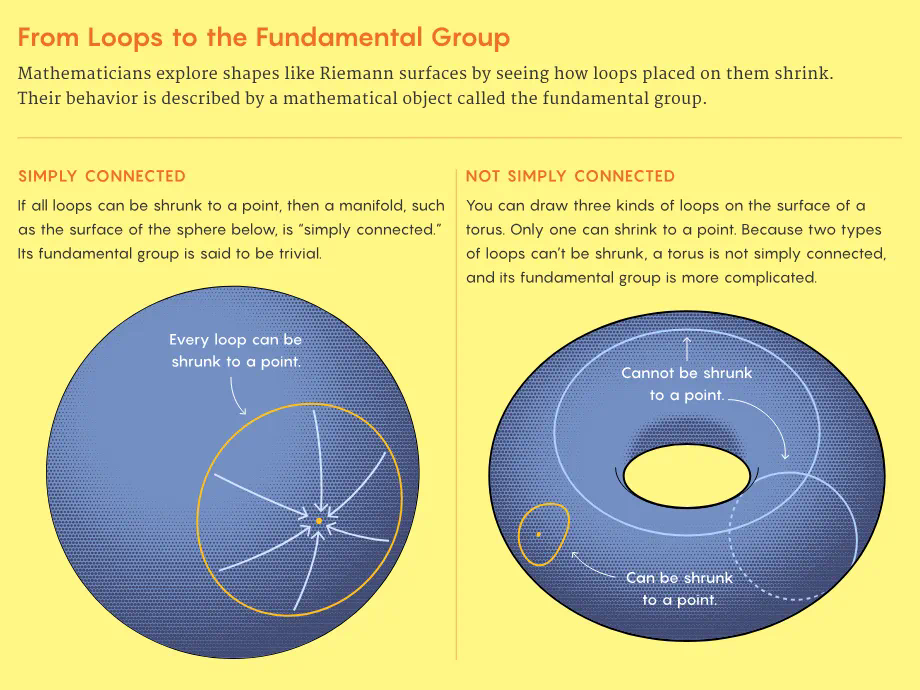
Right from the beginning of Langlands’ work, mathematicians had an idea of what the spectral side of a geometric Langlands correspondence should look like. This third column of Weil’s Rosetta stone concerns compact Riemann surfaces, which are spheres, doughnuts, and doughnuts with multiple holes. A given Riemann surface has a corresponding object called its fundamental group, which tracks the different ways that loops can wind about the surface. Mathematicians suspected that the spectral side of the geometric Langlands correspondence should consist of certain distillations of the fundamental group known as its “representations.”
从 Langlands 的工作开始，数学家们就已经知道了几何 Langlands 对应关系的光谱侧应该是什么样子。Weil 的 Rosetta 石的第三柱涉及致密的黎曼曲面，即球体、甜甜圈和带有多个孔的甜甜圈。给定的黎曼曲面有一个相应的对象，称为其基本群，它跟踪环围绕曲面蜿蜒的不同方式。数学家怀疑，几何朗兰兹对应关系的光谱侧应该由被称为其 “表示” 的基本群的某些提炼组成。

Mark Belan for Quanta Magazine
Mark Belan 为 Quanta Magazine 撰稿

Introduction 介绍

If the Langlands correspondence was to manifest in the geometric column of the Rosetta stone, then each representation of a Riemann surface’s fundamental group should be a frequency label — but of what?
如果朗兰兹对应关系要体现在罗塞塔石的几何柱中，那么黎曼曲面基本群的每个表示都应该是一个频率标签 —— 但是什么呢？

Mathematicians couldn’t find any collection of eigenfunctions whose frequencies seemed to be labeled by the representations of the fundamental group. Then in the 1980s, Vladimir Drinfeld, now at the University of Chicago, realized that it might be possible to create a geometric Langlands correspondence by replacing eigenfunctions with more complicated objects called eigensheaves — even though at the time, he only knew how to construct a few of these.
数学家找不到任何特征函数的集合，其频率似乎由基本群的表示标记。然后在 1980 年代，现在在芝加哥大学的弗拉基米尔・德林菲尔德 （Vladimir Drinfeld） 意识到，通过用更复杂的对象（称为特征层）替换特征函数来创建几何朗兰兹对应关系可能是可能的 —— 尽管当时他只知道如何构造其中的几个。

Sheaves are much more esoteric than functions, and number theorists didn’t know what to make of this proposed geometric cousin of the Langlands correspondence. But the geometric Langlands program, despite the abstruseness of its wave side, has one big advantage over the number theory version of Langlands. In geometric Langlands, the frequency of an eigensheaf is governed by the points on the Riemann surface, and each point on a sphere or doughnut looks pretty similar at close range. But in number theory Langlands, the frequencies are governed by prime numbers, and each prime has unique qualities. Mathematicians don’t know “how to go in a nice way from one prime to another,” said Ana Caraiani, a number theorist at Imperial College London.
滑轮比函数要深奥得多，数论家不知道该如何看待这个提议的 Langlands 对应的几何表亲。但是，几何 Langlands 程序，尽管它的波侧很深奥，但与 Langlands 的数论版本相比，它有一个很大的优势。在几何 Langlands 中，特征束的频率由黎曼曲面上的点控制，球体或圆环上的每个点在近距离内看起来非常相似。但在数论朗兰兹中，频率由素数控制，每个素数都有独特的品质。数学家不知道 “如何以一种好的方式从一个素数转到另一个素数，” 伦敦帝国理工学院的数论家安娜・卡拉亚尼（Ana Caraiani）说。

explainers

What Are Sheaves? 什么是滑轮？

July 19, 2024

Read Later

Riemann surfaces play a large role in physics, particularly in conformal field theory, which governs the behavior of subatomic particles in certain force fields. In the early 1990s, Beilinson and Drinfeld showed how to use conformal field theory to build certain particularly nice eigensheaves.
黎曼曲面在物理学中起着重要作用，特别是在共形场论中，共形场论控制着亚原子粒子在某些力场中的行为。在 1990 年代初期，Beilinson 和 Drinfeld 展示了如何使用共形场理论来构建某些特别漂亮的特征层。

The link to conformal field theory gave Beilinson and Drinfeld a place to start thinking about how to build a version of Fourier analysis for sheaves. “That’s the little grain of sand that this is crystallizing about,” Ben-Zvi said.
与共形场论的联系为 Beilinson 和 Drinfeld 提供了一个开始思考如何构建滑轮傅里叶分析版本的地方。“这就是正在结晶的一小粒沙子，”Ben-Zvi 说。

Beilinson and Drinfeld set forth a rich vision of how the geometric Langlands correspondence should work. It wasn’t only that each representation of the fundamental group should label the frequency of one eigensheaf. This correspondence, they believed, should also respect important relationships on both sides, a prospect Beilinson and Drinfeld took to calling the “best hope.”
Beilinson 和 Drinfeld 对几何 Langlands 对应关系应该如何工作提出了丰富的愿景。这不仅仅是说基本群的每个表示都应该标记一个特征堆的频率。他们认为，这种通信也应该尊重双方的重要关系，贝林森和德林菲尔德将这种前景称为 “最大的希望”。

In the mid-1990s, Beilinson gave a series of lectures on this developing picture at Tel Aviv University. Gaitsgory, then a graduate student there, drank in every word. “I got an imprinting like a new-hatched duckling,” Gaitsgory recalled.
在 1990 年代中期，贝林森在特拉维夫大学就这一发展中的图景进行了一系列讲座。盖茨戈里当时是那里的研究生，他的每一个字都喝得津津有味。“我有一个印记，就像一只刚孵化的小鸭子，” 盖茨戈里回忆道。

In the 30 years since, the geometric Langlands conjecture has been the main driver of Gaitsgory’s mathematical career. “All these years have been nonstop work, getting closer and closer, developing various tools,” he said.
在那之后的 30 年里，几何朗兰兹猜想一直是盖茨戈里数学生涯的主要驱动力。“这些年来，我一直在不停地工作，越来越接近，开发各种工具，” 他说。

The Rising Sea 上升的海平面

Beilinson and Drinfeld had stated their conjecture only loosely, and it turned out that they had been a bit too simplistic about how the relationships in their “best hope” should work. In 2012, Gaitsgory and Dima Arinkin, of the University of Wisconsin, Madison, figured out how make the “best hope” into a precise conjecture. The following year, Gaitsgory wrote an outline of how a proof of the geometric Langlands conjecture might go. That outline relied on a host of intermediate statements, many of which had not yet been proved. Gaitsgory and his collaborators set out to prove them.
Beilinson 和 Drinfeld 只是粗略地陈述了他们的猜想，事实证明，他们对他们 “最大希望” 中的关系应该如何运作有点过于简单化了。2012 年，威斯康星大学麦迪逊分校的 Gaitsgory 和 Dima Arinkin 弄清楚了如何将 “最大的希望” 变成一个精确的猜想。第二年，盖茨戈里写了一份关于几何朗兰兹猜想的证明可能如何进行的大纲。该纲要依赖于一系列中间陈述，其中许多陈述尚未得到证实。盖茨戈里和他的合作者开始证明他们。

Over the next few years, Gaitsgory and Nick Rozenblyum of the University of Toronto wrote two books about sheaves totaling nearly 1,000 pages. Only once in the two-volume set is the geometric Langlands program even mentioned. “But its purpose was to lay the foundations, which we ultimately used very intensively,” Gaitsgory said.
在接下来的几年里，多伦多大学的 Gaitsgory 和 Nick Rozenblyum 写了两本关于滑轮的书，总共近 1000 页。在两卷本的集合中，只有一次甚至提到了几何朗兰兹程序。“但它的目的是奠定基础，我们最终非常密集地使用了这些基础，” 盖茨戈里说。

When Covid-19 struck in 2020, Gaitsgory suddenly found his calendar emptied. “I spent three months lying on my bed and just thinking,” he said. That thinking eventually led to a six-author paper that, while primarily about the function field column of the Langlands program, held the seed of what would later become a crucial component of the proof of the geometric Langlands conjecture: a way to understand how each eigensheaf contributes to what we can think of as “white noise.”
当 Covid-19 在 2020 年来袭时，Gaitsgory 突然发现他的日历是空的。“我花了三个月的时间躺在床上思考，” 他说。这种想法最终导致了一篇由六位作者撰写的论文，虽然这篇论文主要是关于 Langlands 程序的函数场列的，但它为后来成为几何 Langlands 猜想证明的关键组成部分埋下了种子：一种理解每个特征束如何贡献我们可以认为的 “白噪声” 的方法。

Clockwise from left: Dario Beraldo, Lin Chen, Kevin Lin, Nick Rozenblyum, Joakim Færgeman, Justin Campbell and Dima Arinkin.
左起顺时针方向：达里奥・贝拉尔多、林晨、凯文・林、尼克・罗森布柳姆、约基姆・费格曼、贾斯汀・坎贝尔和迪玛・阿林金。

Giancarlo Rado; Yau Mathematical Science Center; Wyatt Reeves; Diana Tyszko; Lisa Smith; Jean Lachat; Alex Arinkin
吉安卡洛・拉多；丘成桐数学科学中心；怀亚特・里夫斯；戴安娜・蒂什科；丽莎・史密斯；让・拉查特；亚历克斯・阿林金

Introduction 介绍

In classical signal processing, sound waves get built up out of sine waves whose frequencies correspond to the pitches contained in the sound. It’s not enough to know which pitches the sound contains — you must also know how loud each pitch is. That information allows you to write your sound as a combination of sine waves: just start with the sine waves of amplitude 1, then multiply each sine wave by an appropriate loudness factor before adding the sine waves together. The sum of all the different amplitude-1 sine waves is what we commonly refer to as white noise.
在经典信号处理中，声波是由正弦波构成的，正弦波的频率对应于声音中包含的音高。仅仅知道声音包含哪些音高是不够的 —— 您还必须知道每个音高有多大。这些信息使您可以将声音编写为正弦波的组合：只需从振幅为 1 的正弦波开始，然后将每个正弦波乘以适当的响度因子，然后再将正弦波相加。所有不同振幅 1 的正弦波之和就是我们通常所说的白噪声。

In the world of the geometric Langlands program, eigensheaves are supposed to play the role of sine waves. Gaitsgory and his collaborators had identified something called the Poincaré sheaf that seemed to be serving the role of white noise. But the researchers didn’t know whether each eigensheaf is even represented in the Poincaré sheaf, let alone whether they all have the same amplitude.
在几何朗兰兹程序的世界里，特征滑轮应该起到正弦波的作用。盖茨戈里和他的合作者发现了一种叫做庞加莱束的东西，它似乎起到了白噪声的作用。但是，研究人员并不知道每个特征堆是否都在庞加莱堆中表示，更不用说它们是否都具有相同的振幅了。

In the spring of 2022, Raskin, together with his graduate student Joakim Færgeman, showed how to use the ideas in the six-author paper to prove that each eigensheaf does contribute to the Poincaré sheaf. “After Sam’s and Joakim’s paper, I was certain we’ll do it within a short period of time,” Gaitsgory said of proving the geometric Langlands conjecture.
2022 年春天，Raskin 和他的研究生 Joakim Færgeman 一起展示了如何使用六位作者论文中的想法来证明每个特征堆确实对庞加莱束做出贡献。“在 Sam 和 Joakim 的论文之后，我确信我们会在很短的时间内完成，”Gaitsgory 在谈到证明几何 Langlands 猜想时说。

The researchers needed to show that all the eigensheaves make equal contributions to the Poincaré sheaf, and that the fundamental-group representations label the frequencies of these eigensheaves. The trickiest part, they came to realize, was handling representations of the fundamental group called irreducible representations.
研究人员需要证明所有特征层对庞加莱束的贡献相等，并且基本群表示标记了这些特征层的频率。他们逐渐意识到，最棘手的部分是处理称为不可约表示的基本群的表示。

The solution for these irreducible representations came to Raskin at a moment when his personal life was filled with chaos. A few weeks after he and Færgeman posted their paper online, Raskin had to rush his pregnant wife to the hospital, then return home to take his son to his first day of kindergarten. Raskin’s wife remained in the hospital until the birth of their second child six weeks later, and during this time Raskin’s life revolved around keeping life normal for his son and driving in endless loops between home, his son’s school and the hospital. “My whole life was the car and taking care of people,” he said.
这些不可简化的表征的解决方案是在拉斯金的个人生活充满混乱的那一刻出现的。在他和 Færgeman 将他们的论文发布到网上的几周后，拉斯金不得不赶紧把怀孕的妻子送到医院，然后回家带儿子去上幼儿园的第一天。拉斯金的妻子一直在医院里，直到六周后他们的第二个孩子出生，在这段时间里，拉斯金的生活围绕着保持儿子的正常生活，并在家、儿子的学校和医院之间无休止地开车。“我的一生就是汽车和照顾人，” 他说。

He took to calling Gaitsgory on his drives to talk math. By the end of the first of those weeks, Raskin had realized that he could reduce the problem of irreducible representations to proving three facts that were all within reach. “For me it was this amazing period,” he said. His personal life was “filled with anxiety and dread about the future. For me, math is always this very grounding and meditative thing that takes me out of that kind of anxiety.”
他开始在开车时打电话给盖茨戈里，让他们聊数学。在那几个星期的第一周结束时，拉斯金已经意识到，他可以将不可简化的表征问题简化为证明三个都可以实现的事实。“对我来说，这是一个了不起的时期，” 他说。他的个人生活 “充满了对未来的焦虑和恐惧。对我来说，数学总是一件非常接地气和冥想的事情，它让我摆脱了那种焦虑。

I spent three months lying on my bed and just thinking.
我花了三个月的时间躺在床上思考。

Dennis Gaitsgory 丹尼斯・盖茨戈里

By early 2023, Gaitsgory and Raskin, together with Arinkin, Rozenblyum, Færgeman and four other researchers, had a complete proof of Beilinson and Drinfeld’s “best hope,” as modified by Gaitsgory and Arinkin. (The other researchers are Dario Beraldo of University College London, Lin Chen of Tsinghua University in Beijing, and Justin Campbell and Kevin Lin of the University of Chicago.) It would take the team another year to write up the proof, which they posted online in February. While the papers follow aspects of the outline Gaitsgory developed back in 2013, they both simplify his approach and go beyond it in many ways. “Very bright people contributed a lot of new ideas to this crowning achievement,” Lafforgue said.
到 2023 年初，Gaitsgory 和 Raskin 以及 Arinkin、Rozenblyum、Færgeman 和其他四名研究人员完全证明了 Beilinson 和 Drinfeld 的 “最大希望”，正如 Gaitsgory 和 Arinkin 所修改的那样。（其他研究人员包括伦敦大学学院的达里奥・贝拉尔多（Dario Beraldo）、北京清华大学的陈林（Lin Chen）以及芝加哥大学的贾斯汀・坎贝尔（Justin Campbell）和凯文・林（Kevin Lin）。该团队还需要一年的时间才能写出证明，并于 2 月份在网上发布。虽然这些论文遵循了 Gaitsgory 在 2013 年制定的大纲的某些方面，但它们都简化了他的方法，并在许多方面超越了它。“非常聪明的人为这一最高成就贡献了很多新想法，” 拉夫福格说。

“It wasn’t just that they went and proved it,” Ben-Zvi said. “They developed whole worlds around it.”
“这不仅仅是他们去证明了这一点，”Ben-Zvi 说。“他们围绕它开发了整个世界。”

Further Shores 更远的海岸

For Gaitsgory, the fulfillment of his decades-long dream is far from the end of the story. A host of further challenges await mathematicians — exploring the connection to quantum physics more deeply, extending the result to Riemann surfaces with punctures, and figuring out the implications for the other columns of the Rosetta stone. “It feels (at least to me) more like that one piece of a big rock has been chipped off, but we are still far from the core,” Gaitsgory wrote in an email.
对于盖茨戈里来说，他长达数十年的梦想的实现远非故事的结局。还有一大堆进一步的挑战等待着数学家 —— 更深入地探索与量子物理学的联系，将结果扩展到带有穿刺的黎曼曲面，并弄清楚对罗塞塔石碑其他柱子的影响。“感觉（至少对我而言）更像是一块大石头被切掉了，但我们离核心还很远，” 盖茨戈里在一封电子邮件中写道。

Researchers working in the other two columns are now eager to translate what they can. “The fact that one of the major pieces has fallen should have major repercussions throughout the Langlands correspondence,” Ben-Zvi said.
在其他两个专栏工作的研究人员现在急于翻译他们能翻译的内容。“其中一个主要部分已经掉落的事实应该对 Langlands 的通信产生重大影响，”Ben-Zvi 说。

Not everything can carry over — for instance, in the number theory and function field settings, there is no counterpart to the conformal field theory ideas that enabled researchers to construct special eigensheaves in the geometric setting. Much of the proof will need serious adjustment before it can be made to work in the other two columns, warned Tony Feng of Berkeley. It remains to be seen, he said, whether “we can even transport the ideas to a different context where it was not designed to work.”
并非所有事物都可以延续 —— 例如，在数论和函数场设置中，没有与共形场论思想相对应的，这些思想使研究人员能够在几何设置中构建特殊的特征层。在可以用于其他两个专栏之前，大部分证据需要进行认真的调整，伯克利的托尼・冯（Tony Feng）警告说。他说，“我们是否甚至可以将这些想法带到一个不同的环境中，在那里它并不是为了工作而设计的。

But many researchers are optimistic that the rising sea of ideas will eventually reach these other domains. “It’s going to seep through all the barriers between subjects,” Ben-Zvi said.
但许多研究人员乐观地认为，不断涌现的思想海洋最终将到达这些其他领域。“它将渗透到主题之间的所有障碍中，”Ben-Zvi 说。

In the past decade, researchers have started turning up unexpected connections between the geometric column and the other two. “If [the geometric Langlands conjecture] had been proved 10 years ago, then the results would be very different,” Feng said. “It wouldn’t have been appreciated that it could potentially have ramifications outside [the geometric Langlands] community.”
在过去的十年中，研究人员已经开始在几何柱和其他两根柱子之间发现意想不到的联系。“如果 [几何朗兰兹猜想] 在 10 年前得到证明，那么结果将会非常不同，” 冯说。“它不会被理解，它可能会在 [几何 Langlands] 社区之外产生影响。”

Gaitsgory, Raskin and their collaborators have already made progress on translating their geometric Langlands proof to the function field column. (Some of the discoveries Gaitsgory and Raskin made on the latter’s long car drives are “still to come,” Raskin hinted.) If successful, this translation will prove a much more precise version of function field Langlands than mathematicians knew or even conjectured before now.
Gaitsgory、Raskin 和他们的合作者在将他们的几何 Langlands 证明转化为函数场列方面已经取得了进展。（拉斯金暗示，盖茨戈里和拉斯金在后者的长途驾驶中发现的一些发现 “仍在后面”。如果成功，这种转化将证明函数域 Langlands 的精确版本比数学家以前知道甚至猜想的要精确得多。

Most translations from the geometry column to the number theory column pass through function fields along the way. But in 2021, Laurent Fargues, of the Mathematics Institute of Jussieu in Paris, and Scholze devised what Scholze called a wormhole that carries ideas from the geometric column directly over to a part of the number theory Langlands program.
从几何列到数论列的大多数转换都在此过程中经过函数字段。但在 2021 年，巴黎 Jussieu 数学研究所的 Laurent Fargues 和 Scholze 设计了 Scholze 所谓的虫洞，将几何列的思想直接传递到数论 Langlands 程序的一部分。

Related: 相关：New Shape Opens ‘Wormhole’ Between Numbers and Geometry
新形状在数字和几何图形之间打开了 “虫洞”Echoes of Electromagnetism Found in Number Theory
在数论中发现的电磁学的回声 The Mathematician Who Delights in Building Bridges
喜欢搭建桥梁的数学家

“I’m definitely one of the people who are now trying to translate all this geometric Langlands stuff,” Scholze said. With the rising sea having spilled over into thousands of pages of text, that is no easy matter. “I’m currently a few papers behind,” Scholze said, “trying to read what they did in around 2010.”
“我绝对是现在试图翻译所有这些几何朗兰兹东西的人之一，” 舒尔茨说。随着海平面上升，已经蔓延到数千页的文字中，这绝非易事。“我目前落后了几篇论文，” 朔尔茨说，“试图阅读他们在 2010 年左右所做的事情。

Now that the geometric Langlands researchers finally have their lengthy proof down on paper, Caraiani hopes they will have more time to talk to researchers on the number theory side. “It’s people who have very different ways of thinking about things, and there’s always a benefit if they manage to slow down and talk to each other and see the other’s perspective,” she said. It’s only a matter of time, she predicted, before the ideas from the new work permeate number theory.
现在，几何 Langlands 的研究人员终于把他们冗长的证明写在纸上了，Caraiani 希望他们能有更多的时间与数论方面的研究人员交谈。“这些人对事情的思考方式截然不同，如果他们设法放慢脚步，互相交谈，看到对方的观点，总会有好处，” 她说。她预测，这只是时间问题，在新工作的思想渗透到数论中之前。

As Ben-Zvi put it, “These results are so robust that once you get started, it’s hard to stop.”
正如 Ben-Zvi 所说，“这些结果是如此强大，以至于一旦你开始，就很难停止。

via:

• Monumental Proof Settles Geometric Langlands Conjecture | Quanta Magazine

  https://www.quantamagazine.org/monumental-proof-settles-geometric-langlands-conjecture-20240719/

朗兰兹纲领

朗兰兹纲领（Langlands program）是数学中一系列影响深远的构想，联系数论、代数几何与约化群表示理论；纲领最初由罗伯特·朗兰兹于1967年在一封给韦伊的信件中提出。 朗兰兹纲领被广泛视为现代数学研究中最大的单项项目，被爱德华·弗伦克尔描述为“数学的一种大统一理论”。

起源：数论

我们可以二次互反律之推广阿廷互反律为朗兰兹纲领之起点： 给定一个Q上的、伽罗瓦群为可交换群的数域，阿廷互反律向这个伽罗瓦群的任何一支一维表示配上一枚L函数，并断言：此等L-函数俱等于某些 狄利克雷L函数（黎曼ζ函数的类推，由狄利克雷特征表达）。此二种L-函数之间的准确的联系构成了阿廷互反律。

若给定不可交换伽罗瓦群及其高维表示，我们仍可定义一些自然的相配的L-函数——阿廷L函数。

推广：自守表示理论架构

朗兰兹洞察到：当找到适当的狄利克雷L-函数的推广，便有可能推广阿廷互反律。

赫克（Erich Hecke）曾联系全纯自守形式（定义于上半复平面上、满足某些函数方程的全纯函数）与狄利克雷L函数。朗兰兹推广赫克理论，以应用于自守尖点表示（自守尖点表示是Q-阿代尔环上一般线性群 GLn 的某类无限维不可约表示）。

朗兰兹为这些自守表示配上L-函数，然后猜想：

若要建立一一对应，须考虑较伽罗瓦群的适当扩张，称作韦依-德利涅群。在可交换的例子，这相当于将狄利克雷特征推广为赫克特征（德文旧称 Größencharakter）。互反猜想蕴含阿廷猜想。

再推广：函子性原则

朗兰兹再进一步推广：

• 以任何连通约化群 G 代替上文中的一般线性群 GLn；
• 构筑复李群 LG（所谓朗兰兹对偶群，或L群）；
• 以自守表示的L包代替自守表示；每个L包是自守表示组成的有限集，属同一L包的表示称作L不可辨的。
• 向每一个 G的自守尖点表示和每一个 LG的有限维表示，配与一个L-函数；同一L包中的表示有相同的 L-函数及 ϵ -因子。朗兰兹并猜想 （页面存档备份，存于互联网档案馆）：此两个 L-函数满足某函数方程。

朗兰兹更构想了一道非常广泛的函子性原则（Functoriality Principle （页面存档备份，存于互联网档案馆））：

函子性猜想蕴含广义拉马努金猜想。

函子性构想本质上是一种诱导表示构造（在传统的自守形式理论中称为提升，在某些特殊情况下已知），因而是协变的（相反地，受限表示构造是逆变的）。各种直接构造的尝试只产生了一些条件性的结果。

上述各猜想亦有其他域上的版本：数域（最早期的版本）、局部域及函数域（即Fp(t)的有限扩张； 其中p 是一 素数 ， Fp(t) 是 p 元有限域上的有理函数域）。局部域的与数域的朗兰兹纲领满足一些相容性，二者之方法亦互为用。

朗兰兹纲领的指导思想

朗兰兹纲领建基于当时已存在的念头：盖尔范德之前几年写的 《尖点形式之启示》（The Philosophy of Cusp Forms）；哈瑞希·昌得拉（Harish-Chandra）研究 半单李群 的结果和方法；而技术上则有塞尔伯格等的塞尔伯格迹公式。

朗兰兹的创见，除技术之深以外，在于他提出上述理论与数论的直接联系，以及其构想中丰富的总体结构（即所谓函子性者也）。

例如在哈瑞希·昌得拉的工作中，我们可见以下原则：

故一旦认清一些低维李群 —如 GL2 —在模形式理论之角色，并反观 GL1 在类域论之角色，我们至少可推测一般 GLn 的情况。

尖点形式之念头来自模曲线上的尖点，在谱理论上对应于离散谱；对比之下连续谱则来自艾森斯坦级数。但当给定的李群越大，则抛物子群越多，技术上则越复杂。

在此等研究途径中不乏各种技巧——通常基于列维分解等事实、具诱导表示的性质 ——但这领域一直都很困难。

在模形式方面，亦有例如希尔伯特模形式、 西格尔模形式 和 theta-级数等等面向。

内窥现象

内窥（英语：Endoscopy）意谓“在一般共轭中窥见稳定共轭”；共轭意谓群的共轭作用 $x\mapsto gx{g}^{-1}$ ；稳定共轭则意谓可取 $g\in G(\bar{F})$ ；稳定共轭类可分解为有限个一般共轭类。稳定共轭与一般共轭之别造成上述的 $L$-不可辨性。

亚瑟-塞尔伯格迹公式是处理函子性猜想及志村簇的哈瑟-韦伊ζ函数之利器。在技术上，我们需要一稳定迹公式，稳定化有赖于将 $G$ 之一般轨道积分表成内窥群上的稳定轨道积分。内窥理论旨在配对群及其内窥群的轨道积分，称作内窥传递；其关键则是所谓的基本引理。

内窥传递不仅是工具，也涵摄函子性猜想的一些特例。

几何朗兰兹纲领

几何朗兰兹纲领(geometric Langlands program)是由数论中的朗兰兹纲领陈述在代数曲线的函数域上而得到的一系列猜想与结论。它联系了代数几何、表示论与量子场论，并对这些学科都产生了深远的影响。在定义于有限域的代数曲线上证明朗兰兹纲领的想法出自于德林费尔德对 ${\mathrm{GL}}_2$ 情形的证明。洛朗·拉福格推广了他的技巧，给出了 ${\mathrm{GL}}_n$ 情形的证明，而后樊尚·拉福格给出了对于一般约化群 $G$ 的自守形式的伽罗华分解。另一方面，柏林森与德林费尔德提出了特征为零的代数曲线上的朗兰兹纲领，并运用无穷维李代数的表示论构造了赫克特征 $D$ -模。阿林金与盖茨哥利根据他们的构造提出了范畴化几何朗兰兹纲领，将伽罗华表示与自守形式之间的关系解释为两个无穷范畴的等价关系。卡普斯汀与爱德华·威滕将黎曼曲面上的几何朗兰兹纲领解释为量子场论的 $S$ -对偶性。

基本想法

根据安德烈·韦伊的想法，数域与黎曼曲面的函数域之间有密切的关系，而定义于有限域 ${\mathbb{F}}_q$ 上的代数曲线与两者都有相似之处。在数域上困难的命题，往往可以在代数曲线、甚至黎曼曲面上陈述并给出证明。几何朗兰兹纲领可以视为数域上的朗兰兹纲领在代数曲线上的表述。

若给定数域 $F$ 和约化群 $G$ ，则自守形式是 $G({\mathbb{A}}_F)$ 上满足特定性质的函数（这里， ${\mathbb{A}}_F$ 指的是 $F$ 的赋值向量环）。朗兰兹纲领的目标是把自守形式联系到伽罗华群 $\mathrm{Gal}(\overline{F}/F)$ 在对偶群 $\check{G}$ 中取值的表示。在定义于 ${\mathbb{F}}_q$ 的代数曲线 $X$ 上，（不分歧的）自守形式应当理解为定义于 $G$ -主丛构成的模空间 ${\mathrm{Bun}}_G$ 的有理点上的 ${\overline{\mathbb{Q}}}_l$ -值函数，而伽罗华表示应当理解为 $X$ 的平展基本群 ${\pi }_1(X)$ 到 $\check{G}$ $\check{G}({\overline{\mathbb{Q}}}_l)$ 的映射。

有限域上的几何朗兰兹纲领

考虑定义在 ${\mathbb{F}}_q$ 上的光滑、射影、几何连通的代数曲线 $X$ 。

几何类域论

在 $G={\mathrm{GL}}_1$ 的情形下，朗兰兹纲领等价于类域论。后者指的是一个拓扑群的同态，称作阿廷互反律(Artin reciprocity)：

$\theta :\mathrm{Pic}({\mathbb{F}}_q)\to {\pi }_1(X{)}_{\mathrm{ab}}$。

这里， ${\pi }_1(X)$ 是曲线 $X$ 的平展基本群， ${\pi }_1(X{)}_{\mathrm{ab}}$ 是它的阿贝尔化。阿廷互反律在投射有限化后会成为同构。不严格地说，几何类域论所表达的现象是 ${\pi }_1(X{)}_{\mathrm{ab}}$ 内所有的关系都由 X 上的亚纯函数给出。

我们现在解释德利涅构造阿廷互反律的方法。首先，通过格罗滕迪克的faisceaux-fonctions对应，若给定概形 $\mathrm{Pic}$ 上的一个平展 ${\overline{\mathbb{Q}}}_l$ -层，则在每一个 ${\mathbb{F}}_q$ 点上，我们可以取弗罗贝尼乌斯自同构的迹而得到一个 ${\overline{\mathbb{Q}}}_l$ -值，这样就能构造 $\mathrm{Pic}({\mathbb{F}}_q)$ 上的一个函数。另一方面，一个映射 ${\pi }_1(X)\to {\overline{\mathbb{Q}}}_l^{\times }$ 可以视为 X 上的光滑 ${\overline{\mathbb{Q}}}_l$ -层 $E$ 。所以，给定 $E$ ，如果我们可以构造 $\mathrm{Pic}$ 上的一个一阶平展 ${\overline{\mathbb{Q}}}_l$ -层（且满足一定性质），那么通过取迹，我们就能构造 $\theta$ 的拓扑对偶：

${\theta }^{\ast }:\mathrm{Hom}({\pi }_1(X),{\overline{\mathbb{Q}}}_l^{\times })\to \mathrm{Hom}(\mathrm{Pic}({\mathbb{F}}_q),{\overline{\mathbb{Q}}}_l^{\times })$

这个方法几何化了阿廷互反律。通过取 $X$ 的交换积，并使用阿贝尔-雅可比映射的性质，德利涅解决了这个几何问题。

一般约化群的情形

在一般约化群的情形下，现在最强的定理由樊尚·拉福格给出，它描述了尖点自守形式的向量空间按伽罗华参量的正交分解：

$C_c^{\mathrm{cusp}}(G(F)\backslash G({\mathbb{A}}_F)/K_N\Xi ;{\overline{\mathbb{Q}}}_l)\stackrel{\sim }{\to }\underset{\sigma }{⨁}{\mathfrak{H}}_{\sigma }$

在 $G={\mathrm{GL}}_n$ 的情形下，上述正交分解由德林费尔德和洛朗·拉福格给出，并且构成了从尖点自守表示到伽罗华表示的一一对应。樊尚·拉福格的定理并不能用来证明朗兰兹所预测的一一对应，所以可以被视为“自守-到-伽罗华”单方面的结果。

我们现在解释上述分解中各项的含义。首先， $F$ 是代数曲线 $X$ 的函数域， ${\mathbb{A}}_F$ 是它的赋值向量环。我们取 $X$ 的一个有限子概形 $N$ ；这是我们考虑的自守形式和伽罗华表示允许分歧的位置。假定 $G$ 是定义在 $F$ 上的分解可约群(split reductive group)，设 $K_N$ 为 $G({\mathbb{O}}_F)\to G({\mathcal{O}}_N)$ 的核， $\Xi$ 为由 $G$ 的中心(center)引出的拓扑群 $Z(F)\backslash Z({\mathbb{A}}_F)$ 中的格(lattice)。左侧的含义是定义在 $G(F)\backslash G({\mathbb{A}}_F)/K_N\Xi$ 上满足尖点性质的 ${\overline{\mathbb{Q}}}_l$ -值紧支撑函数。右侧的下标是伽罗华表示 $\mathrm{Gal}(\overline{F}/F)\to \check{G}({\overline{\mathbb{Q}}}_l)$ （满足如下性质：定义在一个有限扩张 ${\mathbb{Q}}_l\subset E$ 、连续、半单(semisimple)、且在 $N$ 外非分歧）的共轭类。樊尚·拉福格的正交分解可以推广到 $G$ 不分解(non-split)的情形，以及元辛(metaplectic)的情形 $\tilde{G}$ 。

在证明这个分解中，拉福格使用的主要工具是几何佐武同构和德林费尔德的штука。他运用佐武同构构造了一个作用在自守形式上的交换代数 $\mathcal{B}$ ，其元素称为远足算符(excursion operator)。不严格地说， $\mathcal{B}$ 可以被视为伽罗华表示所构成的模空间上的结构层，所以每个伽罗华表示都呈现于他们的共同特征值；上述分解即是向量空间 $C_c^{\mathrm{cusp}}(G(F)\backslash G({\mathbb{A}}_F)/K_N\Xi ;{\overline{\mathbb{Q}}}_l)$ 关于 $\mathcal{B}$ -作用的特征分解。

$\ell$ -进赫克特征层

德利涅对几何类域论的证明启发了一个更强的“伽罗华-到-自守”的几何问题：给定一个 $\check{G}({\overline{\mathbb{Q}}}_l)$ -值的伽罗华表示 E ，是否能构造一个对应于 $E$ 的、定义在代数栈 ${\mathrm{Bun}}_G$ 上的 ${\overline{\mathbb{Q}}}_l$ -层 ${\mathrm{Aut}}_E$ ？为了表述这个对应关系，我们要求 ${\mathrm{Aut}}_E$ 满足以 $E$ 为特征值的赫克特征条件。

在 $G={\mathrm{GL}}_n$ 的情形下，这个构造由弗兰克尔-盖茨哥利-维罗宁给出。它基于一个消灭猜想(vanishing conjecture)。在有限域的情形下，这个消灭猜想可以从洛朗·拉福格的工作中得出。2004年，盖茨哥利给出了消灭猜想的单独证明，从而将赫克特征层的构造推广到任意域的情形。

零特征域上的几何朗兰兹纲领

设 $k$ 是一个特征为零的代数闭域，并考虑定义在 $k$ 上的光滑、射影代数曲线 $X$ 。这一情形下的几何朗兰兹纲领与无穷维李代数的表示论和共形场论密切相关。在零特征域的情形下，自守形式由代数栈 ${\mathrm{Bun}}_G$ 上的 $D$ -模取代。因为弗洛贝尼乌斯同态的缺失，层与函数之间不再具有直接关系，所以零特征域上的朗兰兹纲领不能直接用来获得“古典”信息。

希钦系统的量子化

希钦系统诞生于于微分几何学家奈杰尔·希钦对希格斯场(Higgs field)的研究。他发现由希格斯场构成的模空间上有一个完全可积系统。在代数几何的观点下，希格斯场的模空间可以理解为 ${\mathrm{Bun}}_G$ 的余切空间 $T^{\ast }{\mathrm{Bun}}_G$ 。这一空间具有射向一个向量概形 ${\mathrm{Hitch}}_G$ 的映射：

$h:T^{\ast }{\mathrm{Bun}}_G\to {\mathrm{Hitch}}_G$

而希钦系统由 ${\mathrm{Hitch}}_G$ 上函数的拉回给出。柏林森与德林费尔德提出了这一可积系统的量子化。对于半单群 $G$ ，他们证明了如下结论：若给定一个 $X$ 上具有oper结构的局部系统 $E$ ，则在 ${\mathrm{Bun}}_G$ 上存在一个以 $E$ 为特征值的赫克特征 $D$ -模 $F$。

范畴化几何朗兰兹纲领

范畴化几何朗兰兹纲领(categorical geometric Langlands program)由阿林金与盖茨哥利提出。它有两个分支：局部与全局，且两者都具有量子形变。全局的朗兰兹纲领描述了两个无穷范畴间的等价关系。设 $G$ 为 $k$ 上的约化群， $\check{G}$ 为它的朗兰兹对偶群。我们可以构造两个代数栈：

• $G$ -主丛构成的模空间 ${\mathrm{Bun}}_G$ ；
• $\check{G}$ -局部系统构成的模空间 ${\mathrm{LocSys}}_{\check{G}}$ 。

范畴化几何朗兰兹纲领猜想如下的无穷范畴等价：

${\mathbb{L}}_G:\mathcal{D}\text{-}\mathrm{Mod}({\mathrm{Bun}}_G)\stackrel{\sim }{\to }{\mathrm{IndCoh}}_{\mathrm{Nilp}}({\mathrm{LocSys}}_{\check{G}})$

这里，自守形式方面的范畴由 ${\mathrm{Bun}}_G$ 上的 D -模构成，而伽罗华方面的范畴需要一些额外的解释。首先， $\mathrm{IndCoh}(Y)$ 指的是一个代数栈 $Y$ 上的归纳凝聚层。若 $Y$ 是拟光滑的，则它具有一个奇点栈 $\mathrm{Sing}(Y)$ ，并且任意一个 $Y$ 上的归纳凝聚层 $F$ 都有一个奇支撑 $\mathrm{SingSupp}(\mathcal{F})$ ，是 $\mathrm{Sing}(Y)$ 上的一个锥形闭子集。阿林金与盖茨哥利证明 ${\mathrm{LocSys}}_{\check{G}}$ 是拟光滑的，并且描述了 $\mathrm{IndCoh}({\mathrm{LocSys}}_{\check{G}})$ 中的一个闭子集 $\mathrm{Nilp}$ ，称为全局幂零锥(global nilpotent cone)。在上述等价中，伽罗华方面的范畴 I${\mathrm{IndCoh}}_{\mathrm{Nilp}}({\mathrm{LocSys}}_{\check{G}})$ 指的是 $\mathrm{IndCoh}({\mathrm{LocSys}}_{\check{G}})$ 中由奇支撑属于 $\mathrm{Nilp}$ 的归纳凝聚层构成的完全子范畴。伽罗华方面幂零锥的出现可以理解为数论中亚瑟参量的几何体现。上述无穷范畴间的等价可以用来实现赫克特征 $\mathcal{D}$ -模的构造；对于任意一个 $X$ 上的 $\check{G}$ -局部系统 $E$ ，它对应于 ${\mathrm{LocSys}}_{\check{G}}$ 上的一个skyscraper层，于是它在 L G 下的像即是以 $E$ 为特征值的赫克特征 D -模。

在 $G={\mathrm{GL}}_1$ 时，上述等价关系即是傅立叶-向井-洛蒙变换。在 $G={\mathrm{GL}}_2$ 的情形下，盖茨哥利给出了上述等价关系的证明题纲。范畴化几何朗兰兹的研究在很大程度上需要依靠导出代数几何的工具。

量子几何朗兰兹纲领

为了描述全局几何朗兰兹纲领的量子形变，需要引入带旋 $\mathcal{D}$ -模 (twisted D-module)的概念。对于一个光滑的代数簇 $X$ ，一个带旋 $\mathcal{D}$ -算子是一个带有 ${\mathbb{Z}}_{\ge 0}$ 流 (filtration)的结合代数层，其关联有次代数与 $X$ 的切丛 $TX$ 所生成的对称代数作为泊松代数同构。该代数的模称为带旋 $\mathcal{D}$ -模。这一定义可以拓张到任何光滑代数栈。 为了说明的简便，在本节中我们限制 $G$ 是一个单群，并引入以下记号：

• $\mathfrak{g}$ 是 $G$ 所对应的李代数；
• $h^{\vee }$ 是 $\mathfrak{g}$ 的对偶考克斯特数(dual Coxeter number)；
• $r$ 是 $\mathfrak{g}$ 的带数(lacing number)，亦即其登金图中相邻两顶点间最大的边数；
• 对于任何 $c\in k$ ，令 $[c]=\frac{c-h^{\vee }}{2h^{\vee }}$ 。

在这种情况下，对于每一个 $c\in k$ （对应于 $\mathfrak{g}$ 所对应的仿射李代数的一个中心扩张），存在一个 ${\mathrm{Bun}}_G$ 上的带旋 D -算子 ${\mathcal{D}}^c$ ，对应于 ${\mathcal{L}}_{\det }^{[c]}$ 到自身的微分算子，其中 ${\mathcal{L}}_{\det }$ 是 ${\mathrm{Bun}}_G$ 上的自带的行列式线丛。其对应的带旋 $\mathcal{D}$ -模范畴记作 $\mathcal{D}\text{-}{\mathrm{Mod}}^c({\mathrm{Bun}}_G)$ 。

在柏林森与德林费尔德对量子化希钦系统的研究中，赫克特征 $\mathcal{D}$ -模自然处于的范畴是对应于临界值(critical level) c = 0 （对应于 $[c]=-\frac{1}{2}$ 的 $\mathcal{D}$ -模范畴，而该范畴与 [ c ] = 0 的范畴（亦即上文中的 $\mathcal{D}\text{-}\mathrm{Mod}({\mathrm{Bun}}_G)$ ）等价。而另一方面，伽罗华侧的对象 ${\mathrm{IndCoh}}_{\mathrm{Nilp}}({\mathrm{LocSys}}_{\check{G}})$ 的某种近似 $\mathcal{D}\text{-}{\mathrm{Mod}}^c({\mathrm{Bun}}_{\check{G}})$ 在 $c\to \infty$时同构。这自然地引出几何朗兰兹纲领是否可以沿着 c 的方向形变的问题。量子全局几何朗兰兹纲领猜想如下的无穷范畴等价：

${\mathbb{L}}_G^c:\mathcal{D}\text{-}{\mathrm{Mod}}^c({\mathrm{Bun}}_G)\stackrel{\sim }{\to }\mathcal{D}\text{-}{\mathrm{Mod}}^{-\frac{1}{rc}}({\mathrm{Bun}}_{\check{G}})$

这一猜想亦隐式地出现于卡普斯汀与威滕对于几何朗兰兹纲领的物理诠释中。

via: encyclopedia