机器学习算法逻辑回归（LR）的学习与应用（疾病问诊）

实验目的

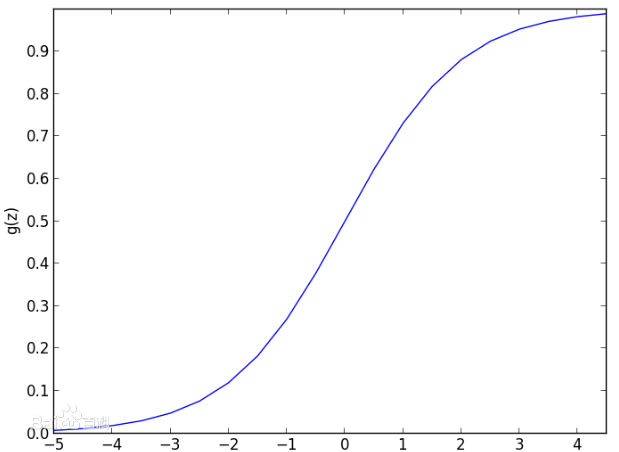
逻辑回归(Logistic Regression, LR)模型其实仅在线性回归的基础上，套用了一个逻辑函数，但也就由于这个逻辑函数，使得逻辑回归模型成为了机器学习领域一颗耀眼的明星，更是计算广告学的核心。单纯的使用线性回归去对数据进行分类，系统的鲁棒性很差，所以一般会对线性回归的结果做一个逻辑函数的映射，在这里，逻辑函数为sigmoid函数，函数模型为S形：

实验介绍

语言： Python

GitHub地址： luuuyi/logistic_regression

实验步骤

1）原理介绍

回归是一种极易理解的模型，就相当于y=f(x)，表明自变量x与因变量y的关系。最常见问题有如医生治病时的望、闻、问、切，之后判定病人是否生病或生了什么病，其中的望闻问切就是获取自变量x，即特征数据，判断是否生病就相当于获取因变量y，即预测分类。

但是对于一个单纯的线性模型，分类效果受数据集噪点的影响，分类表现不会特别突出，但是通过增加一个结果对于逻辑函数的映射，在辅与优化方法，能够很好地对训练数据集进行收敛训练，最终得到一个依托于训练数据集求出的最完美的参数集合。

具体介绍可以百度或者参考以下两篇博文：

逻辑回归

逻辑回归模型基础

2）简单实现

①梯度上升方法

照惯例，先简单实现以下LR的核心代码：

def sigmoid(in_datas):
    return 1.0/(1.0+exp(-in_datas))

def gradientAscent(datas,labels):
    datas_mat = mat(datas)
    labels_mat = mat(labels).transpose()
    h, w = shape(datas_mat)
    alpha = 0.001
    max_iter = 500
    weights = ones((w,1))
    for i in range(max_iter):
        res = sigmoid(datas_mat*weights)
        errors = (labels_mat - res)
        weights = weights + alpha*datas_mat.transpose()*errors          #梯度上升变形，朝着标准标签的方向缓慢移动
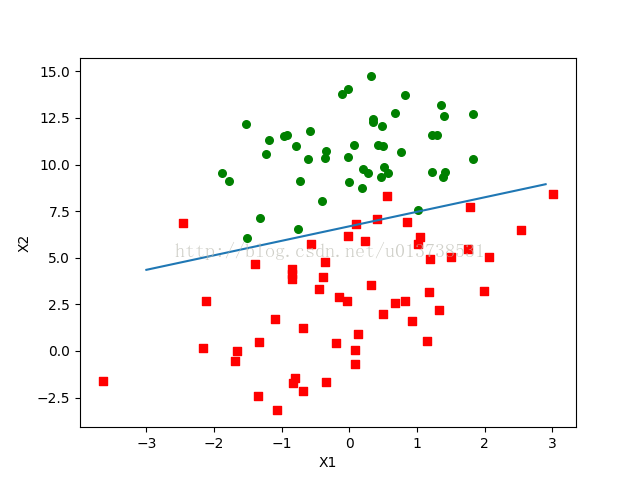
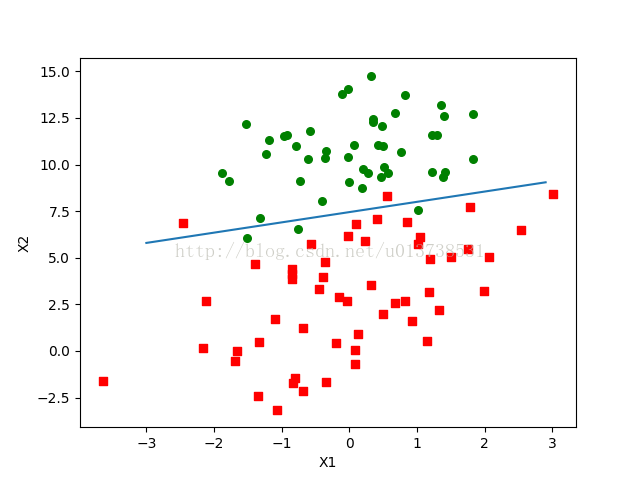
    return weights

第一个是逻辑函数，也就是sigmoid函数的实现；第二个是梯度上升的训练方法，对于数据集，与初始的模型参数做线性运算之后将结果通过sigmoid函数映射到（0,1）区间，对于一个简单的二分类问题，正样本为1，负样本为0，当结果处于（0,1）区间范围内时，可以通过结果与端点的差值，反向调整权值数据，最终目的是缩小这一差值，达到收敛，这里使用的是梯度上升的方法去迭代500次计算，学习率为0.001，之后对模型进行可视化表现：

可以看出分类还是比较准确的，只有两个数据被错误分类。

②随机梯度上升

但是这其实是对于整个数据集进行划分，每一次迭代的时候都读入了所有的数据集进行计算，当样本量和特征维度特别大的时候计算耗时特别久，虽然能得出很好的结果，但是开销太大。现在介绍一个随机梯度上升的优化方法；系统每一次在数据集中随机选择一条数据进行训练，训练次数为样本总数：

def randomGradientAscent(datas,labels):
    datas_arr = array(datas)            #array和matrix有区别
    h, w = shape(datas_arr)
    alpha = 0.01
    weights = ones(w)                   #一维矩阵
    for i in range(h):
        res = sigmoid(sum(datas_arr[i]*weights))
        errors = labels[i] - res
        weights = weights + alpha*errors*datas_arr[i]
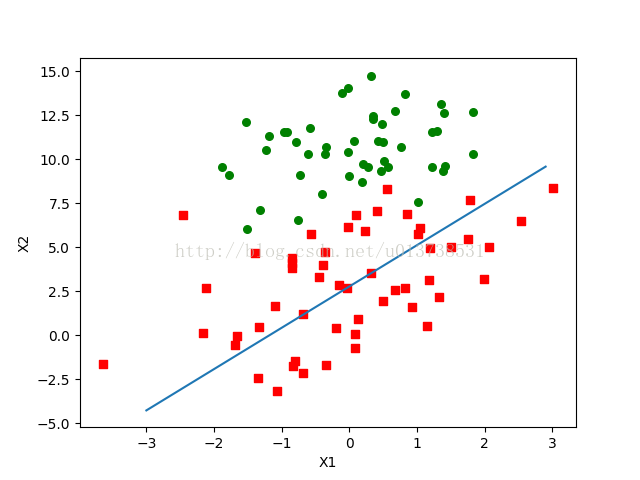
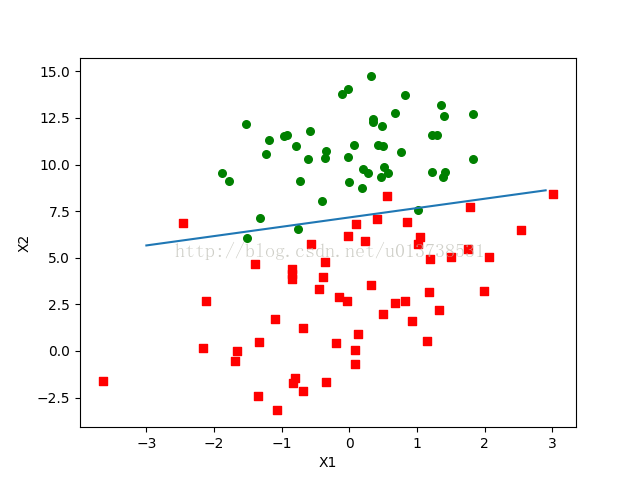
    return weights

对结果可视化看一下：

可以看出训练效果并没有上一个那么理想，但这其实并不能说明什么，上一个参数值是通过了500次迭代，每一次都是对整个训练样本数据集进行计算的结果，计算量之间没有可比性，结果也没有代表意义。

③改进的随机梯度上升

但是随机梯度上升方法一个好处就是，训练系统对于数据集，无论有多少样本，或者是样本的特征维度有多大，都有很好的计算优势，因为每一次只用读取一条数据进行训练，对于之后新采集到的样本也能加入其中。基于这个基础，我们改进了一下该方法：

def advancedRandomGradientAscent(datas,labels,iter_nums=150):
    import random
    datas_arr = array(datas)           
    h, w = shape(datas_arr)
    weights = ones(w)                  
    for i in range(iter_nums):
        indexs = range(h)
        for j in range(h):
            alpha = 4/(1.0+j+i)+0.01
            random_index = int(random.uniform(0,len(indexs)))
            res = sigmoid(sum(datas_arr[random_index]*weights))
            errors = labels[random_index] - res
            weights = weights + alpha*errors*datas_arr[random_index]
            del(indexs[random_index])
    return weights

大体上和上一个函数差不多，不同点在于首先在学习率上，将不再使用一个固定的值，通俗点来说体现在与随着迭代次数的增加，权值向着标准位置偏移的步幅变缓，能这样理解，经过多次迭代之后，其实系统的分类能力已经趋于稳定，当前训练的权值相对于标准的权值来说已经无限接近了，步幅太大会导致权值在标准权值左右大幅振动，可能带来误差，为了能够得到一个很好的收敛效果，可以适当降低学习率。

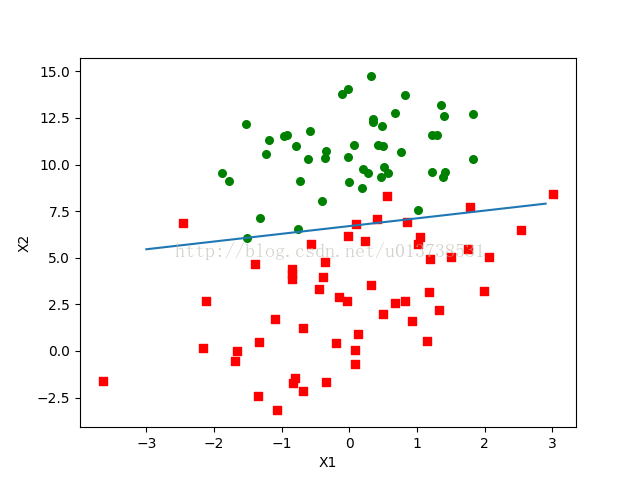
来看一下分类效果的可视化结果：

可以看出改进的随机梯度上升方法，在迭代次数为150次的时候其实效果已经比较理想了，但是与第一个500次迭代的结果还是有一点点差距。

当将迭代次数改为500次和1000次之后又会发生什么样的变化：

500次：

1000次：

其实效果上倒是没有多大的改进了，不过在一些临界数据的分类上会更加的细致，由此能看出到模型趋于稳定的情况下，单纯提高迭代次数对于模型的优化改进已经不是特别明显了；对于数据集中的一些噪点干扰，LR回归模型还是不能做到绝对的线性可分；

3）场景应用

这里使用了一份网上的数据，为马匹疝病的诊断数据，将其一分为二，一部分为训练数据，一部分为测试数据，原数据中每一行（每一条数据）有21个特征，最后的0,1标签代表是否致死，通过对训练数据的迭代训练，我们构建一个简单的分类模型，进而使用模型对测试集进行模型误差分析。

def colicTest():
    fd_train = open('horseColicTraining.txt')
    fd_test = open('horseColicTest.txt')
    train_datas=[]; train_labels=[]
    for line in fd_train.readlines():
        line_data_list = line.strip().split('\t')
        tmp_list=[]
        for i in range(21):
            tmp_list.append(float(line_data_list[i]))
        train_datas.append(tmp_list)
        train_labels.append(float(line_data_list[21]))
    weights = advancedRandomGradientAscent(train_datas,train_labels,500)
    error_count = 0; total_size = 0.0
    for line in fd_test.readlines():
        total_size += 1.0
        line_data_list = line.strip().split('\t')
        test_data = []
        for i in range(21):
            test_data.append(float(line_data_list[i]))
        if int(classifyResult(array(test_data),weights)) != int(line_data_list[21]):
            error_count += 1
    error_rate = float(error_count)/total_size
    print "The Error Ratio is: %f" % error_rate
    return error_rate

通过对前面介绍的几个函数集合整理，得到上面这个分析函数，最终的输出结果为：

上面的警告为浮点数位数计算溢出了，解决方法可以使用Python pip安装一个叫做bigfloat的包，在安装之前还要给系统先配置一个什么环境，反正是一个C++的库，有兴趣可以去看一下；

结果为38%，看起来好像很糟糕，但其实不然，这份数据其实是通过一个残缺的数据集修复得到的，关于数据集的修复，网上还有学术界有大量的研讨资料，这里使用的方法是残缺数据补0的做法，因为补0并不会对回归的权值更新带来额外的问题，回顾一下这条代码：

weights = weights + alpha*errors*datas_arr[random_index]

在做权值更新的时候，某一条数据的某一维特征假如说因为残缺补全为0，那么在这一维的梯度上升计算中，他结果为0，也就是该数据的该特征对于权值的更新没有贡献，它不影响权值的结果，这是一个比较折中同时也比较保守的方法，因为对于最终结果是没有贡献的。

最后，博主最近开始学习机器学习，希望结识更多的有识之士一起探讨交流，下一章研究SVM。