分解质因数

定义

• 质因数分解是将一个大于1的整数写成一些质数的乘积的过程。
• 每个合数（即非质数的整数）都有唯一的一种质因数分解方式，不计因子的顺序。

运用情况

• 数学运算：如求最大公约数（GCD）和最小公倍数（LCM）时，质因数分解非常有用。
• 简化分数：通过质因数分解分子和分母，可以更容易地约简分数。
• 解方程：在解决某些代数方程时，质因数分解可以帮助找到未知数的值。
• 算术基本定理：每个大于1的整数要么是一个质数，要么可以唯一地表示为一组质数的乘积。

注意事项

• 分解时，应从最小的质数开始尝试除法，通常先除以2，然后是3，接着是5等。
• 当一个数不能被任何小于它的平方根的质数整除时，这个数就是质数。
• 质因数分解可能需要多次尝试不同的质数，直到所有因子都被分解出来。

解题思路

1. 选择最小的质数：从2开始，看它是否能整除给定的数。
2. 持续除法：如果可以整除，就不断除以这个质数，直到不能再整除为止。
3. 移动到下一个质数：一旦当前的质数不能整除了，就尝试下一个质数（例如3，5，7...）。
4. 重复步骤：继续上述过程，直到最后剩下的数是一个质数。
5. 记录结果：将所有的质数因子按照它们出现的次数记录下来。

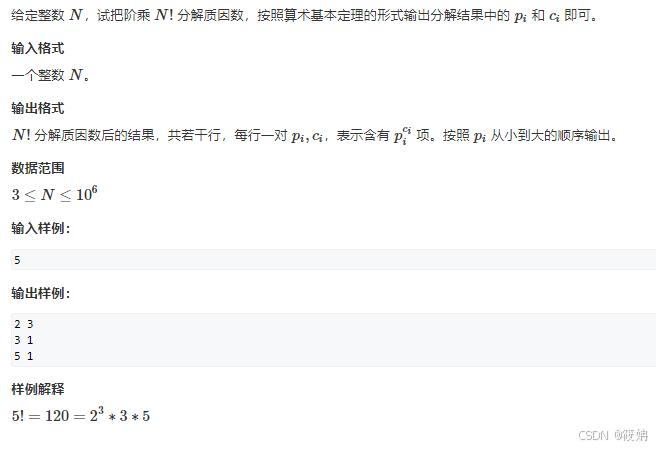
AcWing 197. 阶乘分解 

题目描述

197. 阶乘分解 - AcWing题库

运行代码

#include <iostream>
using namespace std;

const int MAXN = 1000006;
int primes[MAXN], cnt;
bool st[MAXN];

void get_primes(int n) {
    for (int i = 2; i <= n; i++) {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] * i <= n; j++) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int main() {
    int n;
    cin >> n;
    get_primes(n);
    int c[MAXN] = {0};
    // 优化：只计算每个质数在 n! 中的出现次数
    for (int i = 0; i < cnt; i++) {
        int p = primes[i];
        int num = 0;
        for (int j = p; j <= n; j += p) {
            int x = j;
            while (x % p == 0) {
                num++;
                x /= p;
            }
        }
        c[i] = num;
    }
    for (int i = 0; i < cnt; i++) {
        if (c[i]) cout << primes[i] << " " << c[i] << endl;
    }
    return 0;
}

代码思路

1. 初始化和获取质数:

   • get_primes函数使用了埃拉托斯特尼筛法（Sieve of Eratosthenes）来找出从2到n之间的所有质数，并存储在primes数组中。
   • st数组用于标记哪些数已经被筛掉（即非质数），而cnt用于跟踪已经找到的质数数量。

2. 计算质因数在n!中的幂次:

   • 主函数main中，首先读入一个整数n，然后调用get_primes函数来获得所有不大于n的质数。
   • 接着，对于每一个质数p，程序计算出p在n!中作为因子出现了多少次。
   • 这是通过遍历从p到n的每个数，检查每个数能够被p整除多少次来实现的。每次能够整除时，计数器num增加，直到该数不再能被p整除。

3. 输出结果:

   • 最后，遍历所有找到的质数及其在n!中出现的次数，并将它们输出。如果某个质数在n!的质因数分解中出现，则输出该质数及其对应的次数。

注意：代码中的注释“优化：只计算每个质数在 n! 中的出现次数”意味着，代码并没有直接计算n!，而是计算了n!的质因数分解，这比直接计算阶乘更有效率，因为阶乘的值会变得非常大，可能会超出计算机可以处理的范围。

改进思路

其它代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1000010;

int primes[N], cnt;
bool st[N];

void init(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] * i <= n; j ++ )
        {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int main()
{
    int n;
    cin >> n;
    init(n);

    for (int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        int s = 0;
        for (int j = n; j; j /= p) s += j / p;
        printf("%d %d\n", p, s);
    }

    return 0;
}

代码思路

1. 初始化质数列表:

   • init函数使用埃拉托斯特尼筛法（Sieve of Eratosthenes）来生成小于等于nn的所有质数，并存储在primes数组中。
   • st数组用于标记哪些数已被筛去（即已知的合数）。
   • 当遇到一个新的质数ii，它会被添加到primes数组中，并且所有它的倍数都会被标记为合数。

2. 计算质因数在n!n!中的幂次:

   • 在main函数中，首先读取一个整数n，然后调用init函数生成所有小于等于n的质数。
   • 遍历生成的质数列表，对于每个质数pp，使用一个循环计算pp在n!n!中作为因子出现的总次数。
   • 这个次数可以通过不断除以pp并累加商的方式计算，直到商小于1为止。具体地，对于每个pp，s初始化为0，然后使用一个循环，每次将j除以p，并将商加到s上，直到j不足以再被p整除。

3. 输出结果:对于每个质数pp和它在n!n!中出现的次数p和s，使用printf函数输出这对质数和次数。

代码优化点

• 使用Legendre公式计算每个质数在n!n!中的幂次，避免了原始代码中对于每个数都做一次完整的质因数分解，大大减少了计算量。
• 使用printf和scanf（虽然这里只用了cin）通常比cout和cin快，尤其是在大量数据的输入输出时。