HDU1753——大明A+B

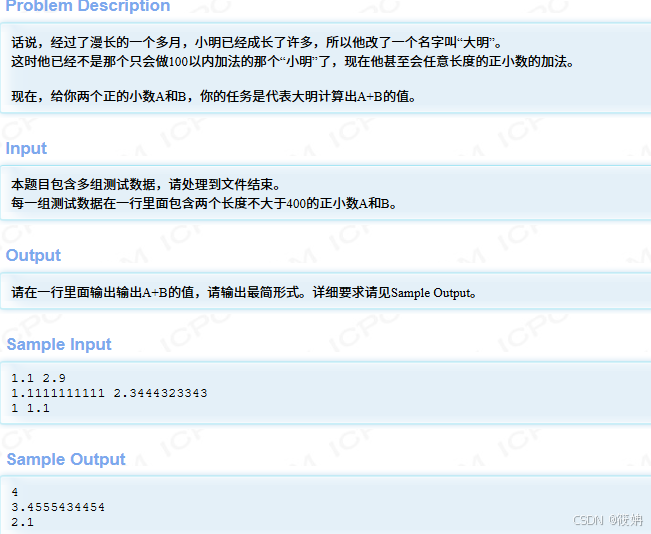
题目描述

Problem - 1753 (hdu.edu.cn)

运行代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <map>
#define ll long long
using namespace std;

char a[505], b[505];
int a1[505], b1[505];
int sum[505];

int main() {
    while (~scanf("%s %s", a, b)) {
        memset(sum, 0, sizeof(sum));
        int p = -1, q = -1, pd = 0, qd = 0;
        int kk = -1;
        int i = 0;
        // 处理小数点后的部分
        while (a[i] && a[i]!= '.') i++;
        if (a[i] == '.') {
            pd = 1;
            for (i++; a[i]; i++) a1[++p] = a[i] - '0';
        }
        i = 0;
        while (b[i] && b[i]!= '.') i++;
        if (b[i] == '.') {
            qd = 1;
            for (i++; b[i]; i++) b1[++q] = b[i] - '0';
        }
        // 补零使小数点后位数相同
        if (p < q) {
            for (int i = p + 1; i <= q; i++) a1[i] = 0;
            p = q;
        } else if (p > q) {
            for (int i = q + 1; i <= p; i++) b1[i] = 0;
            q = p;
        }
        // 小数点后相加
        for (int i = p; i >= 0; i--) {
            sum[++kk] += a1[i] + b1[i];
            if (sum[kk] > 9 && i!= 0) {
                sum[kk + 1]++;
                sum[kk] -= 10;
            }
        }
        // 处理小数点前的部分
        p = q = -1;
        for (i = 0; a[i] && a[i]!= '.'; i++) a1[++p] = a[i] - '0';
        for (i = 0; b[i] && b[i]!= '.'; i++) b1[++q] = b[i] - '0';
        // 小数点后可能进位
        if (sum[kk] > 9) {
            sum[kk + 1]++;
            sum[kk] -= 10;
        }
        kk++;
        sum[kk + 1] = sum[kk];
        sum[kk] = -1;
        if (kk == -1) kk = 0;
        // 小数点前数字相加
        if (p == q) {
            for (int i = p; i >= 0; i--) {
                sum[++kk] += a1[i] + b1[i];
                if (sum[kk] > 9) {
                    sum[kk + 1]++;
                    sum[kk] -= 10;
                }
            }
        } else if (p > q) {
            while (p >= 0 && q >= 0) {
                sum[++kk] += a1[p] + b1[q];
                if (sum[kk] > 9) {
                    sum[kk + 1]++;
                    sum[kk] -= 10;
                }
                p--;
                q--;
            }
            for (int i = p; i >= 0; i--) {
                sum[++kk] += a1[i];
                if (sum[kk] > 9) {
                    sum[kk + 1]++;
                    sum[kk] -= 10;
                }
            }
        } else if (p < q) {
            while (p >= 0 && q >= 0) {
                sum[++kk] += a1[p] + b1[q];
                if (sum[kk] > 9) {
                    sum[kk + 1]++;
                    sum[kk] -= 10;
                }
                p--;
                q--;
            }
            for (int i = q; i >= 0; i--) {
                sum[++kk] += b1[i];
                if (sum[kk] > 9) {
                    sum[kk + 1]++;
                    sum[kk] -= 10;
                }
            }
        }
        // 去除前导零和后导零
        int j = 0;
        while (sum[j] == 0) j++;
        if (sum[kk + 1]) kk++;
        if (sum[kk] == 0 && sum[kk - 1]!= -1) kk--;
        for (int i = kk; i >= j; i--) {
            if (sum[i] == -1 && i!= j) printf(".");
            else if (sum[i]!= -1) printf("%d", sum[i]);
        }
        printf("\n");
    }
    return 0;
}

代码思路

一、整体思路

这段代码的目的是实现两个数字字符串的加法运算，允许输入的数字字符串包含小数点，并且可以处理小数点前后不同位数的情况。

1. 首先，分别读取两个数字字符串 a 和 b。
2. 然后，将两个数字字符串分为小数点前和小数点后两部分分别进行处理。对于小数点后的部分，找到两个数字字符串中小数点的位置，提取出小数点后的数字部分，进行补零操作使得小数点后的位数相同，然后逐位相加，处理进位情况。对于小数点前的部分，同样提取出数字部分，根据位数的不同情况进行逐位相加，同样处理进位情况。
3. 最后，去除结果中的前导零和后导零，并输出结果。

二、具体步骤原理

1. 输入与初始化通过 while (~scanf("%s %s", a, b)) 循环不断读取两个数字字符串。使用 memset(sum, 0, sizeof(sum)) 初始化存储结果的数组 sum。设置一些变量如 p、q、pd、qd、kk 等用于记录小数点位置和位数等信息。

2. 处理小数点后的部分

   • 遍历数字字符串 a 和 b，找到小数点的位置，如果存在小数点，则记录下小数点后的数字部分到数组 a1 和 b1 中，并设置标志 pd 和 qd。
   • 如果两个数字字符串小数点后的位数不同，通过补零操作使得它们的位数相同。
   • 逐位相加 a1 和 b1 中的数字，将结果存储在 sum 数组中，同时处理进位情况。

3. 处理小数点前的部分

   • 再次遍历数字字符串 a 和 b，提取小数点前的数字部分到数组 a1 和 b1 中。
   • 如果小数点后的相加产生了进位，需要在处理小数点前的部分时考虑进去。
   • 根据两个数字字符串小数点前的位数情况，分为相等、第一个字符串位数多、第二个字符串位数多三种情况进行逐位相加，并处理进位情况。

4. 去除前导零和后导零并输出结果

   • 找到结果中第一个非零数字的位置，去除前导零。
   • 如果结果的最高位为零且不是唯一的数字，去除后导零。
   • 遍历结果数组 sum，输出最终的加法结果，遇到标记为小数点的位置输出小数点。

HDU1115——Lifting the Stone

题目描述

Problem - 1115 (hdu.edu.cn)

运行代码

#include <iostream>
#include <iomanip>
#include <cmath>
const int N = 1000005;
struct Point {
    double x, y;
};

Point barycenter(Point* points, int n) {
    Point p = points[0];
    double area = 0.0, tpx = 0.0, tpy = 0.0;
    for (int i = 1; i <= n; ++i) {
        Point s = points[(i == n) ? 0 : i];
        double tp = (p.x * s.y - s.x * p.y);
        area += tp / 2;
        tpx += (p.x + s.x) * tp;
        tpy += (p.y + s.y) * tp;
        p = s;
    }
    Point result;
    result.x = tpx / (6 * area);
    result.y = tpy / (6 * area);
    return result;
}

int main() {
    int t, n;
    std::cin >> t;
    while (t--) {
        std::cin >> n;
        Point points[N];
        for (int i = 0; i < n; i++) {
            std::cin >> points[i].x >> points[i].y;
        }
        Point ss = barycenter(points, n);
        std::cout << std::fixed << std::setprecision(2) << ss.x << " " << ss.y << '\n';
    }
    return 0;
}

代码思路

一、整体思路

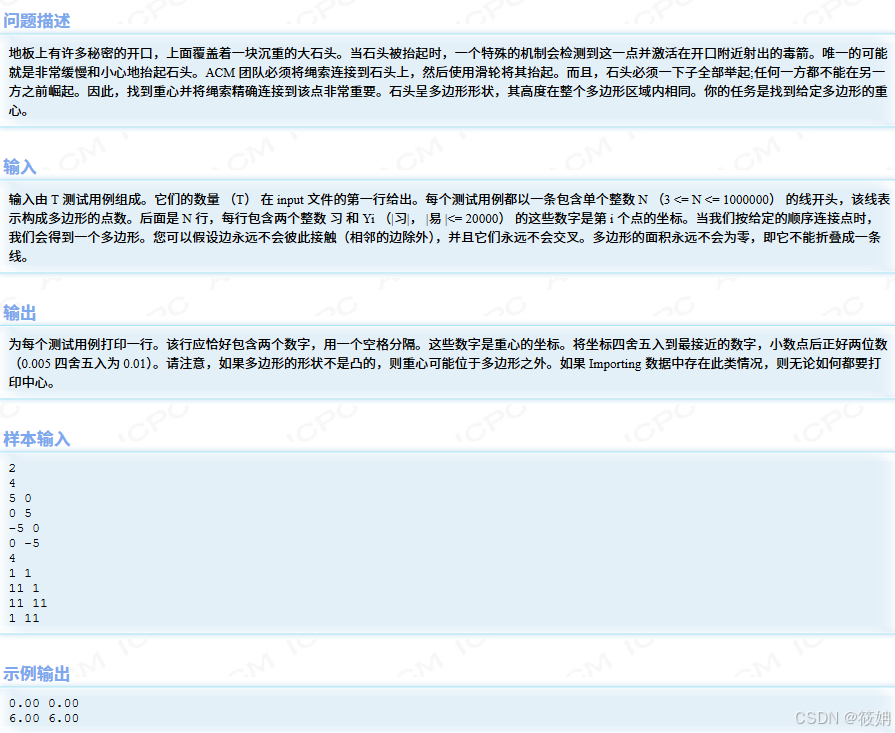
这段代码的目的是计算给定多边形的重心。多边形由一系列点表示，代码通过遍历多边形的各个边，利用向量叉积的方法来计算多边形的面积和重心坐标。

二、具体步骤原理

1. 定义结构体和函数

   • 定义了一个结构体 Point 来表示点的坐标，包含两个成员变量 x 和 y。
   • 定义了一个函数 barycenter，用于计算多边形的重心。这个函数接受一个指向 Point 结构体数组的指针和多边形的点数作为参数，并返回一个 Point 结构体表示重心坐标。

2. 主函数 main

   • 首先读取测试用例的数量 t。
   • 对于每个测试用例：读取多边形的点数 n。读取 n 个点的坐标，存储在 Point 结构体数组 points 中。调用 barycenter 函数计算多边形的重心，并将结果存储在 ss 中。输出重心坐标，保留两位小数。

3. 计算重心的函数 barycenter

   • 初始化一些变量：p 初始化为第一个点。area 初始化为 0.0，用于累加多边形的面积。tpx 和 tpy 初始化为 0.0，分别用于累加重心坐标在 x 和 y 方向上的贡献。
   • 遍历多边形的各个边：对于每个边，取当前点和下一个点（如果是最后一个点，则取第一个点）作为 s。计算当前边和第一个点组成的三角形的有向面积 tp，通过向量叉积公式 (p.x * s.y - s.x * p.y) 计算。将 tp 累加到总面积 area 中（注意面积是有向的，需要除以 2）。计算重心坐标在 x 和 y 方向上的贡献，分别累加 (p.x + s.x) * tp 到 tpx 和 (p.y + s.y) * tp 到 tpy。
   • 计算重心坐标：最终的重心坐标 result.x 等于 tpx / (6 * area)，result.y 等于 tpy / (6 * area)。这里的 6 * area 是根据重心的计算公式推导出来的系数。
   • 返回重心坐标。

HDU1140——War on Weather

题目描述

问题 - 1140 (hdu.edu.cn)

运行代码

#include <iostream>
#include <cmath>
const int N = 1000005;
const double pi = acos(-1.0);

struct Point {
    double x, y, z;
};

double dist(Point a, Point b) {
    return std::pow(a.x - b.x, 2) + std::pow(a.y - b.y, 2) + std::pow(a.z - b.z, 2);
}

int main() {
    int n, m;
    double R = 20000.0 / pi;
    while (std::cin >> n >> m) {
        if (n == 0 && m == 0) break;
        Point points[N];
        for (int i = 0; i < n; ++i) {
            std::cin >> points[i].x >> points[i].y >> points[i].z;
        }
        int cnt = 0;
        for (int i = 0; i < m; ++i) {
            Point p;
            std::cin >> p.x >> p.y >> p.z;
            for (int j = 0; j < n; ++j) {
                double D2 = points[j].x * points[j].x + points[j].y * points[j].y + points[j].z * points[j].z;
                double L2 = D2 - R * R;
                if (dist(points[j], p) <= L2) {
                    cnt++;
                    break;
                }
            }
        }
        std::cout << cnt << '\n';
    }
    return 0;
}

代码思路

一、整体思路

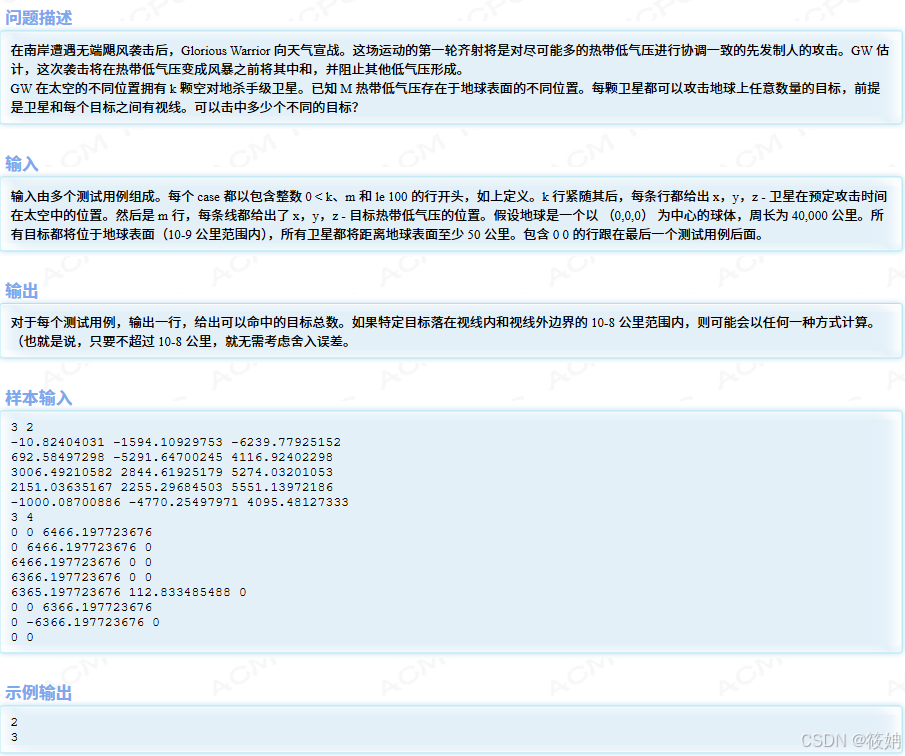
这段代码的目的是计算在给定的卫星和目标点的情况下，有多少目标点在卫星的特定范围内。

1. 首先定义了一个点的结构体 Point，包含三个坐标 x、y、z。
2. 定义了一个函数用于计算两个点之间的距离平方（dist函数）。
3. 在主函数中，通过循环读取多个测试用例。每个测试用例包含卫星数量 n 和目标数量 m。
4. 对于每个测试用例，读取卫星的坐标并存储在数组中。然后遍历目标点，对于每个目标点，检查它是否在某一个卫星的特定范围内，如果在，则增加命中目标的计数。最后输出命中目标的总数。

二、具体步骤原理

1. 常量定义和结构体定义：定义圆周率 pi 和点的结构体 Point。圆周率用于后续计算地球半径的相关值。

2. 距离计算函数 dist：接受两个点作为参数，通过计算它们在三个维度上的坐标差的平方和来得到两点之间的距离平方。

3. 主函数 main

   • 定义地球半径 R，其值是通过一个特定的公式计算得出（这里 20000.0/pi 的含义可能与问题背景中的地球周长等因素相关）。
   • 通过 while(std::cin >> n >> m) 循环不断读取测试用例的卫星数量 n 和目标数量 m。如果 n 和 m 都为 0，则跳出循环。
   • 对于每个测试用例：
     • 读取 n 个卫星的坐标存储在 points 数组中。
     • 初始化命中目标计数 cnt 为 0。
     • 遍历 m 个目标点：读取目标点的坐标。对于每个卫星，计算卫星到地心的距离平方 D2，然后计算一个与卫星半径相关的阈值 L2。如果目标点到当前卫星的距离平方小于等于 L2，说明目标点在该卫星的范围内，增加命中目标计数 cnt 并跳出当前内层循环，因为一个目标点只需要被一个卫星命中即可。
   • 输出当前测试用例中命中目标的总数 cnt。