背景&基本思想介绍
在实际的评价类问题中,在前面所说的层次分析法以及Topsis法中,指标权重的确定往往是通过主观的评价得来的,如果在没有专家的情况下,我们自己的权重分配往往可能带有一定的主观性,有没有一种可以客观确定指标的权重的方法呢?这就是本次要介绍的熵权法的由来。
总的来说,从方法的名字来看我们可以知道,所谓熵,就是离散或者说混乱程度,熵权法的核心思想在于,我们可以通过一个指标在不同的评价对象上的离散程度来确定这个指标的重要性。这样讲可能有点抽象,下面我来举一个例子帮助大家理解。
假如现在要对几个不同的城市的空气质量情况进行评估排名,每个城市在进行评价的时候有如下几个指标:第一个是PM2.5浓度,第二个是空气能见度,第三个是空气中含氮化合物的浓度,第四个是含硫化合物的浓度,在这几个城市中经过调查,发现他们的含氮化合物的浓度基本一致,那么大家想一想,当我们在进行评估的时候,极端情况下,假如我们只能拿出一个指标来评判,我们会拿含氮化合物浓度这个指标来进行评估吗?相信大家肯定都不会选择这个指标,理由很简单,因为这几个城市都是一样的,那怎么进行评价呢?
所以相信大家能够从这个例子中大概了解到熵权法的一些思想,所谓离散程度,就是指这个指标在几个对象的身上的差异大不大,差异越大,离散程度越大,那么这个指标在评价的过程中,所能发挥的作用越大;反之,如果差异不大,离散程度越低,那么这个指标对评价的帮助就越小。我们肯定是要给帮助大的指标分配更多的权重,给帮助越小的分配更少的权重,这就是熵权法的基本思想。
方法具体实现
在所有的工作开始前,我么还要偶先对指标进行正向化处理,这一点在Topsis法的文章中有提及,大家可以看一下这个文章:数学建模笔记(2):Topsis分析法。
矩阵的标准化处理
首先还是一样,标准化的目的就是消除量纲的影响,这一点在前面的文章中已经有所提及,由于不同的物理量的单位不同,因此我们要消除因为单位不同所带来的数据上的差异影响。
这里采用的方法还是和Topsis法的处理方法一样,即用每一个指标所在的列的平方和的二次方根作为分母,每一个元素除以该列所有元素的平方和的二次方根即可。(PS:这里的矩阵,每一行是一个评价对象,每一列是一个指标)。
概率矩阵计算
虽然这个概率矩阵的名字听起来挺唬人,但是本质上就是在前面的标准化矩阵的基础上,再对每一列(指标是列)进行归一化处理,即每一列的元素除以这列元素的和,让这个列所有的元素的和为一即可。
计算熵权
这里的熵权是针对每一个指标来说的,具体的公式如下:

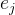
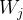
这样的话,最终的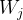
代码实现
下面是熵权法的MatLab代码,供大家参考,是我自己写的,难免会有错误,还请大家指正。
clc;
clear;
X=input("请输入正向化后的指标矩阵:");
[n,m]=size(X);
%对矩阵进行标准化操作
for i=1:size(X,2)
judge=find(X<0); %find函数如果找不到在矩阵X中小于0的数就会返回空
if isempty(judge)
Z(:,i)=X(:,i)/(sum(X(:,i).^2).^(1/2));%针对没有负数的情况,采用的是每一列除以这一列的平方和的归一化方法
else
Z(:,i)=(X(:,i)-min(X(:,i)))/(max(X(:,i))-min(:,i)); %有负数就采用这种办法
end
end
%另外一种标准化的代码
%Z=X./repmat(sum(X.*X).^0.5,n,1);%相当于是先利用sum函数是计算得到矩阵的每一列之和,得到每列和开方的行向量,再把这个行向量沿着行方向复制n次得到一个和原来矩阵大小一样的矩阵,进行逐项相除。
disp("标准化后的矩阵为:")
disp(Z);
%计算熵权
for j=1:m
P(:,j)=Z(:,j)/sum(Z(:,j));%对标准化后的矩阵进行归一化,即每一列之和都变为1
e(j)=-sum(P(:,j).*mylog(P(:,j)))/log(n);%按照公式计算熵权
d(j)=1-e(j);
end
disp("归一化后的矩阵为:")
disp(P);
disp("每个指标的熵权为:")
disp(e);
disp(d);
W=d/sum(d); %对熵权进行归一化处理
disp("最终经过归一化处理的熵权为:")
disp(W);
由于害怕出现log函数中有0的情况,还有一个mylog函数文件
function [res]=mylog(j)
n=length(j);
res=zeros(n,1);
for i=1:n
if j(i)==0
res(i)=0;
else
res(i)=log(j(i));
end
end
end好了以上就是熵权法的介绍,希望能够得到大家的一键三连~~~

