哈夫曼编码主要用于数据压缩，通常可以节省20%-90%的空间，具体的压缩率依赖于数据的特性。下面举个简单的例子说明对于字符不同编码方式所使用的空间大小。

从图中可以看出：

1、定长编码6个字符使用的二进制位数为 （45*3+13*3+12*3+16*3+9*3+5*3）= 300 个二进制位来编码文件。

2、变长编码中6个字符使用的二进制位数为 （45*1+13*3+12*3+16*3+9*4+5*4） = 224 个二进制位来编码文件。

3、变长编码与定长编码相比节约了(300-224)/300 = 25%的空间。

哈夫曼编码是有贪心算法来构造的最优前缀码。哈夫曼编码是通过二叉树的形式构造表示的，其中构造出的二叉树一定是一颗满二叉树。

下面简述哈夫曼编码的构造过程：

1、由给定的m个权值{w(1),w(2),w(3),...,w(m)}，构造m课由空二叉树扩充得到的扩充二叉树{T(1),T(2),....T(m)}。每个T(i)(1<= i <= m)只有一个外部节点（也是根节点），它的权值置为m(i)。概括一下就是把原先的节点封装成二叉树结点的形式。

2、在已经构造的所有扩充二叉树中，选取根结点的权值最小和次最小的两棵，将他们作为左右子树，构造成一棵新的扩充二叉树，它的根结点（新建立的内部结点）的权值置为其左、右子树根结点权值之和。

3、重复执行步骤（2），每次都使扩充二叉树的个数减少一，当只剩下一棵扩充二叉树时，它便是所要构造的哈夫曼树。

下面是哈夫曼编码的具体操作步骤：

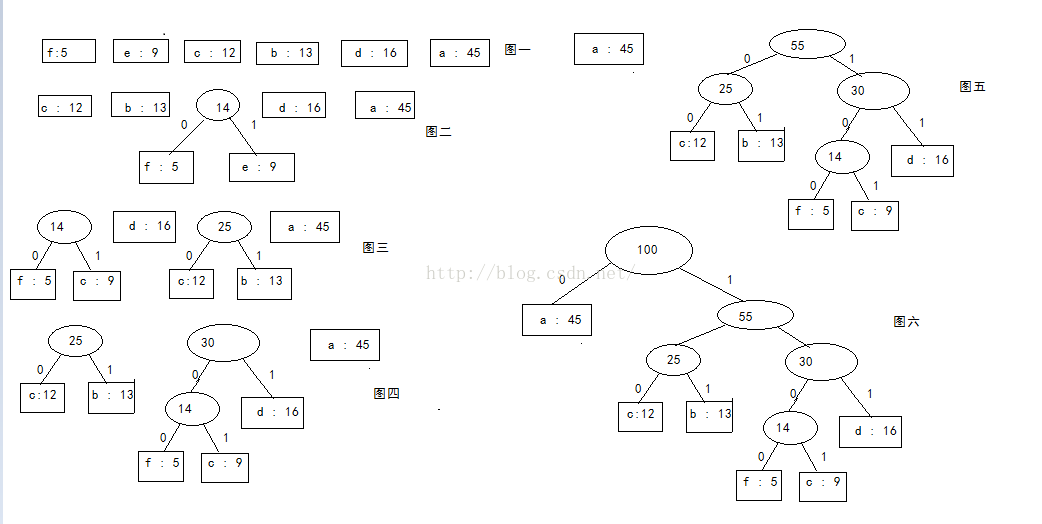
从图中可以看出，每次选择两个最小的结点，生成新的二叉树之后，新二叉树的根结点重新加入到原结点序列中。