欧几里得算法
欧几里德算法又称辗转相除法,用于计算两个整数a,b的最大公约数。基本算法:设a=bq+r,其中a,b,q,r都是整数,则gcd(a,b)=gcd(b,r),即gcd(a,b)=gcd(b,a%b)。
证明引自离散数学课本:
先看一个整除定理与推论:
接下来是证明过程:
代码实现:
int gcd(int a,int b)
{
if(b==0)
{
return a;
}
return gcd(b,a%b);
}现在我们知道了 a 和 b 的最大公约数是 gcd ,那么,我们一定能够找到这样的 x 和 y ,使得: a*x + b*y = gcd 这是一个不定方程(其实是一种丢番图方程),有多解是一定的,但是只要我们找到一组特殊的解 x0 和 y0 那么,我们就可以用 x0 和 y0 表示出整个不定方程的通解:
x = x0 + (b/gcd)*t
y = y0 – (a/gcd)*t
为什么不是:
x = x0 + b*t
y = y0 – a*t
那是因为:
b/gcd 是 b 的因子, a/gcd 是 a 的因子是吧?那么,由于 t的取值范围是整数,你说 (b/gcd)*t 取到的值多还是 b*t 取到的值多?同理,(a/gcd)*t 取到的值多还是 a*gcd 取到的值多?那肯定又要问了,那为什么不是更小的数,非得是 b/gcd 和a/gcd ?
注意到:我们令 B = b/gcd , A = a、gcd , 那么,A 和 B 一定是互素的吧?这不就证明了 最小的系数就是 A 和 B 了吗?
现在,我们知道了一定存在 x 和 y 使得 : a*x + b*y = gcd , 那么,怎么求出这个特解 x 和 y 呢?只需要在欧几里德算法的基础上加点改动就行了。
扩展欧几里得算法
扩展欧几里德算法是欧几里得算法的扩展。
定理:若a和b为正整数,则存在整数x,y使得gcd(a,b)=ax+by;
换句话说gcd(a,b)可以表示为a,b的整洗数线性组合,例如:gcd(6,14)=2,而2=(-2)*6+1*14.
已知整数a、b,扩展欧几里得算法可以在求得a、b的最大公约数的同时,能找到整数x、y(其中一个很可能是负数),使它们满足贝祖等式ax+by=gcd(a,b).有两个数a,b,对它们进行辗转相除法,可得它们的最大公约数,然后,收集辗转相除法中产生的式子,倒回去,可以得到ax+by=gcd(a,b)的整数解。
用类似辗转相除法,求二元一次不定方程252x+198y=18的整数解。
252=1*198+54
198=3*54+36
54=1*36+18
36=2*18
用倒数第二个除法(正数第三个),可以把gcd(254,198)=18表示为54和36的线性组合,即
18=54-1*36
第二个除法说明:
36=198-3*54
将36的这一表达式带入前一等式,可以把18表示为54和198的线性组合,也就是:
18=54-1*36=54-1*(198-3*54)=4*54-1*198.
第一个除法说明:
54=252-1*198.
带入上面等式:
18=4*(252-1*198)-1*198=4*252-5*198.
结论问题得解:x=4,y=-5.
基本算法:对于不完全为 0 的非负整数 a,b,gcd(a,b)表示 a,b 的最大公约数,必然存在整数对 x,y ,使得 gcd(a,b)=ax+by。
欧几里德算法停止的状态是: a= gcd , b = 0 //1
推理2,ab!=0时
设 ax1+by1=gcd(a,b);
bx2+(a%b)y2=gcd(b,a%b);
根据朴素的欧几里德原理有 gcd(a,b)=gcd(b,a%b);
则:ax1+by1=bx2+(a%b)y2;
即:ax1+by1=bx2+(a-(a/b)*b)y2=ay2+bx2-(a/b)*by2;
令a/b=k;
得ax1+by1=bx2+(a-k*b)y2=ay2+b(x2-k*y2)=ay2+b(x2-a/b*y2);
根据恒等定理得:x1=y2; y1=x2-(a/b)*y2; //2
这样我们就得到了求解 x1,y1的方法:x1,y1的值基于 x2,y2.
上面的思想是以递归定义的,因为 gcd不断的递归求解一定会有个时候 b=0,所以递归可以结束。
扩展欧几里德的递归代码:
#include <iostream>
#include <stdio.h>
using namespace std;
int exgcd(int a,int b,int &x,int &y)
{
if(b==0)
{ //1的情况
x=1;
y=0;
return a;
}
int r=exgcd(b, a%b, x, y);
int t=y;
y=x-(a/b)*y; //2的情况
x=t;
return r;
}
int main()
{
int x,y;
exgcd(252,198, x, y);
cout<<"252x+198y=18的一个整数解为:"<<endl;
cout<<"x="<<x<<" "<<"y="<<y<<" "<<endl;
return 0;
}扩展欧几里德的非递归代码:
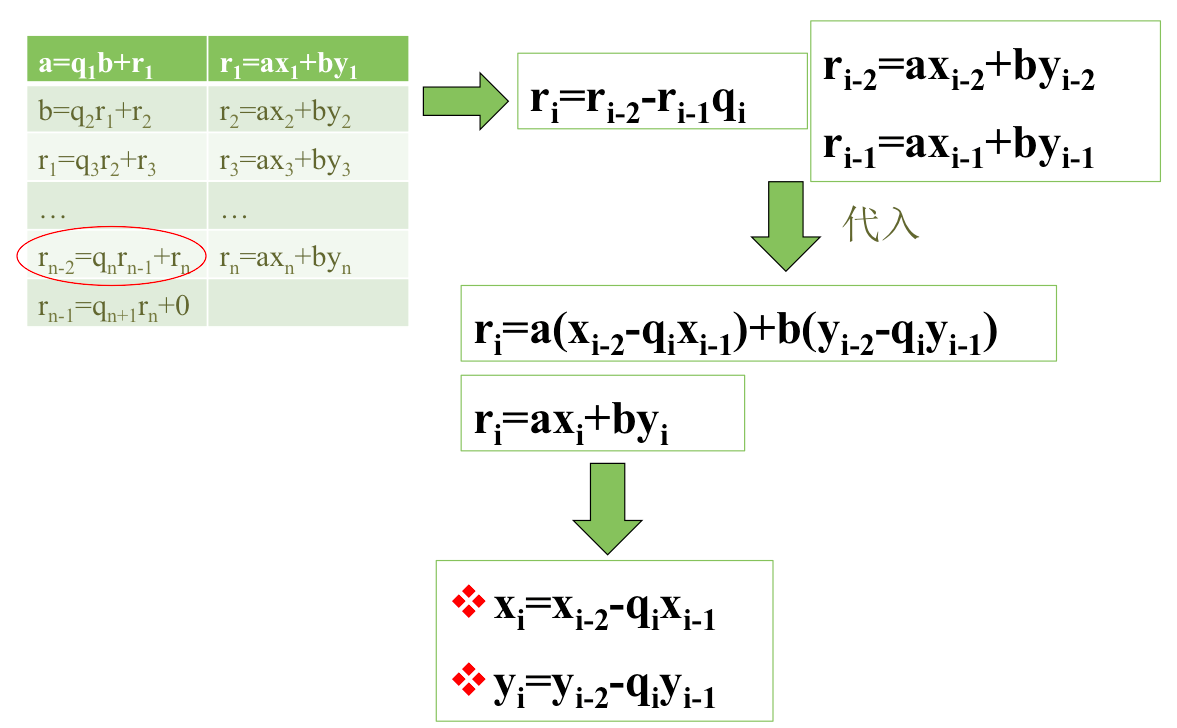
先来理解下面推的公式。
int exgcd(int a,int b,int &x,int &y)
{
int xi_1,yi_1,xi_2,yi_2;
xi_2=1,yi_2=0;
xi_1=0,yi_1=1;
x=0,y=1;
int r=a%b;
int q=a/b;
while (r)
{
x=xi_2-q*xi_1;
y=yi_2-q*yi_1;
xi_2=xi_1;
yi_2=yi_1;
xi_1=x,yi_1=y;
a=b;
b=r;
r=a%b;
q=a/b;
}
return b;
}扩展欧几里德算法的应用
扩展欧几里德算法的应用主要有以下三方面:
(1)求解不定方程;
(2)求解模的逆元;
(3)求解模线性方程(线性同余方程);
一、解不定方程
对于不定整数方程pa+qb=c,若 c mod gcd(p, q)=0,则该方程存在整数解,否则不存在整数解。
上面已经列出找一个整数解的方法,在找到p * a+q * b = gcd(p, q)的一组解p0,q0后,p * a+q * b = gcd(p, q)的其他整数解满足:
p = p0 + b/gcd(p, q) * t
q = q0 - a/gcd(p, q) * t(其中t为任意整数)
至于pa+qb=c的整数解,只需将p * a+q * b = gcd(p, q)的每个解乘上 c/Gcd(p, q) 即可。
在找到p * a+q * b = gcd(a, b)的一组解p0,q0后,应该是得到p * a+q * b = c的一组解p1 = p0*(c/Gcd(a,b)),q1 = q0*(c/Gcd(a,b)),
p * a+q * b = c的其他整数解满足:
二、求乘法逆元
如果a×b≡1 mod n,则a、b互为乘法逆元(也就是(a*b)%n=1)。
若a与b不互素,则a模b没有乘法逆元!
一般,我们能够找到无数组解满足条件,但是一般是让你求解出最小的那组解,怎么做?我们求解出来了一个特殊的解 x0 那么,我们用 x0 % m其实就得到了最小的解了。为什么?
可以这样思考:
x 的通解不是 x0 + n*t(n>=0的整数) 吗?
那么,也就是说, a 关于 m 的逆元是一个关于 m 同余的,那么根据最小整数原理,一定存在一个最小的正整数,它是 a 关于m 的逆元,而最小的肯定是在(0 , m)之间的,而且只有一个,这就好解释了。
可能有人注意到了,这里,我写通解的时候并不是 x0 + (m/gcd)*t ,但是想想一下就明白了,gcd = 1,所以写了跟没写是一样的,但是,由于问题的特殊性,有时候我们得到的特解 x0 是一个负数,还有的时候我们的 m 也是一个负数这怎么办?
当 m 是负数的时候,我们取 m 的绝对值就行了,当 x0 是负数的时候,他模上 m 的结果仍然是负数(在计算机计算的结果上是这样的,虽然定义的时候不是这样的),这时候,我们仍然让 x0 对abs(m) 取模,然后结果再加上abs(m) 就行了,于是,我们不难写出下面的代码求解一个数 a 对于另一个数 m 的乘法逆元:
int cal(int a,int n)
{
int x,y;
int gcd(ex_gcd(a, n, x, y));
if(1%gcd!=0)
{
return -1;
}
x*=1/gcd;
n=abs(n);
int ans=x%n;
if(ans<=0)
ans+=n;
return ans;
}