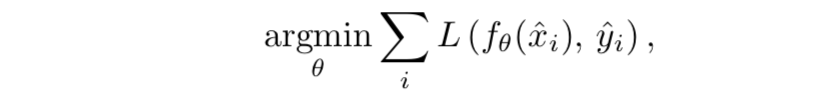知乎同名账号同步发表

无/自监督去噪(2)——Noise2Noise (N2N) 理论分析(从损失函数入手)

1. 前沿

N2N，即Noise2Noise: Learning Image Restoration without Clean Data，2018 ICML的文章。
N2V，即Noise2Void - Learning Denoising from Single Noisy Images，2019 CVPR的文章。

这两个工作都是无监督去噪的重要开山之作，本文先对其进行简单总结，然后引出一个变体：HQ-SSL（2019 NIPS）。

本系列会对近一两年的顶会顶刊无监督图像恢复（主要是去噪）工作、时间有点久远但是非常经典的无监督图像恢复工作进行学习总结。欢迎大家评论交流、关注、批评。

2. N2N

相信大家对这句话不算陌生：同一场景下的两次含噪声的观测（noisy observation）。

上图就是该方法的训练策略，$x_i$和$y_i$分别表示同一个场景下的两次相互独立的含噪声的观测。$f_{\theta }(\cdot )$表示网络。

为什么这样训练就能让$f_{\theta }(\cdot )$学会去噪呢？这是因为有如下假设：

• 第一，噪声零均值假设；
• 第二，$x_i$和$y_i$是同一场景下的两次观测；
• 第三，不同次的含噪声的观测之间，噪声相互独立。

为了简便起见，我们将一张noisy image表示为如下形式：
$$image=signal+noise$$
即含噪声的图片是由信号和噪声想加而成（这样不严谨，因为噪声未必是加性噪声，但是此处为了方便，我们可以这样阐述）。我们可以将$x_i$和$y_i$分别用上述形式表示如下：
$$x_i=s_i+x{n}_i,y_i=s_i+y{n}_i$$
我们将$x_i$和$y_i$两张图片都表示为信号+噪声的形式，再用前文的损失函数，即网络尝试学会将$x_i$映射为$y_i$。由于噪声相互独立这一假设，$x{n}_i$和$y{n}_i$毫无关联，但由于这是同一场景下的两次观测，所以两者中信号的部分都用$s_i$表示。

网络尝试学会将$x_i$映射为$y_i$，就是将$s_i+x{n}_i$映射为$s_i+y{n}_i$：
$$f_{\theta }(x_i)=f_{\theta }(s_i+x{n}_i)\to s_i+y{n}_i$$
由于$x{n}_i$和$y{n}_i$毫无关联，将$x{n}_i$映射为$y{n}_i$是不可能的。此时用数学语言表述，网络的输出可以表示为如下形式：
$$f_{\theta }(x_i)=f_{\theta }(s_i+x{n}_i)\to s_i+随机噪声$$
网络并没有办法建立xn_i和yn_i的联系，这种$随机\to 随机$的映射，最终会演变为$随机\to E(随机)$的映射。由于噪声零均值这一假设，上式可以进一步写为：
$$f_{\theta }(x_i)=f_{\theta }(s_i+x{n}_i)\to E(s_i+随机噪声)=s_i+E(随机噪声)=s_i$$

所以，只要满足噪声零均值假设、两次观测x和y在同一场景下、两次观测的噪声相互独立，那么就可以通过让网络学习从x映射到y的方式学会去噪。作者亦通过实验证明了有效性。

3. N2V——盲点网络（BSNs，Blind Spot Networks）开创者

N2V可以视为对N2N的批判，理由如下：

N2N的训练数据是相同场景的两次不同noisy observation组成的pair，实际使用的时候，两次不同的观测很难是相同场景的。比如医学图像，两次拍摄的时间不一样，也许器官在位置上发生了细微的变化，这就不能叫做严格的相同场景。

以上的问题，核心在于训练需要两张noisy image。那么能否只用一张noisy image就完成训练呢？当然可以，其实N2N之后涌现了Neighbor2Neighbor、N2V这样优秀的工作，这些都可以不必依赖于noisy image pair，而是依赖于single noisy image就能够完成训练。Neighbor2Neighbor是对一张noisy image进行采样得到pair，然后采用N2N的方式进行训练，并通过loss消除location gap；N2V则完全采用了和N2N不一样的思路，接下来我们主要介绍一下N2V，因为它是BSNs的开创者（to my best knowledge，所以此说法如有不对请评论区指出）。

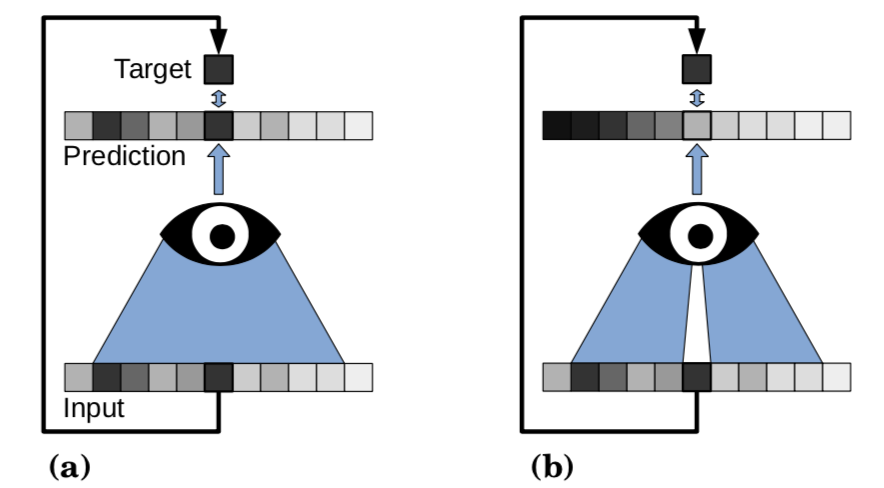
这是N2V论文中的图，在有监督学习中，给网络输入Input，获得Prediction，通过让Prediction接近GT，就能够让网络学会去噪。如果是无监督，那么这个Label是不存在的。如上图左侧（a），由于Prediction最终要接近Input，所以网络会学习恒等映射。但是我们的目标就是中single noisy image完成训练，既没有GT，也没有相同场景下的另一个噪声观测，实验要怎么做呢？

我们可以选择如上图（b）的做法，对比图（a）的感受野，我们将（b）中的感受野的中心部分挖掉一个像素，然后将剩余的部分作为Input，我们记为$Inpu{t}_{blind}$。由于网络看不到Input的中心像素点，我们称这个像素点为Blind Spot，也就是盲点。所有存在盲点的方法，我们都可以归类为Blind Spot Networks，也就是BSNs。我们将没有挖掉中心像素的Input记为$Inpu{t}_{total}$，网络的输出Prediction和$Inpu{t}_{total}$做loss，就可以促进网络学会去噪。

所以，N2V就讲完了（bushi…

简单说一下，我们只需要对Input做一件事——挖掉它的中心像素，然后扔给网络。网络的输出和Input之间的差距作为loss，就能让网络学会去噪。但是，这一切是有前提的，N2V有如下假设：

（我们依旧将像素视为信号+噪声）

• 不同像素位置，信号是相互有关联的；
• 不同像素位置，噪声是相互没有关联的（在一些文章中称为噪声独立假设）；
• 噪声的均值为0。

网络可以看到除了中心像素以外的全部像素，包括它们的信号和噪声。网络实际学习的事情就是：如何根据周围的像素点，推测出中心像素点。由于不同像素位置的信号互有关联，比如你鼻孔边缘像素的附近可能是鼻屎，鼻子像素的附近可能有黑头，所以通过周围像素的信号，可能可以推测出中心像素的信号；但是依据噪声独立假设，无法通过周围像素的噪声推测出中心像素的噪声。所以将网络输出的中心像素$x_{pre}$和Input中被屏蔽的中心像素$x_{in}$做loss：
$$x_{pre}-x_{in}=s_{pre}+n_{pre}-(s_{in}+n_{in})=s_{pre}-s_{in}+(n_{pre}-n_{in})$$
s和n分别表示信号和噪声。为了表述方便，上式直接用了减法。根据在N2N部分的讲解，相信你已经猜到了网络的输出会是如下形式：
$$x_{pre}=s_{pre}+n_{pre}\to E(s_{in}+随机噪声)=s_{in}+E(随机噪声)$$
根据噪声零均值假设，我们有：
$$x_{pre}\to s_{in}+E(随机噪声)=s_{in}$$

3.1. N2V实际是如何训练的？

上文所述，我们将Input中心像素点挖掉，并让网络的输出和完整的Input做loss。可是这样会导致每次只有一个像素影响训练过程。此部分我们简单讲下N2V原文是如何训练模型的。

N2V实际的训练方式：随机选取$64\times 64$大小的patch，记为x。在x中随机选取N个点，对每个点p，都随机用一个点的像素替换它（具体地，在以p为中心、以网络感受野为大小的区域，如上图（b），用该区域内的一个随机像素（蓝色）替换中心像素（红色））。这样，x中就被创造了N个盲点，将这样的x记为$x_{blind}$。将$x_{blind}$输入到网络，获得输出记为y。我们将x中N个点和y中对应位置的N个点做loss。这样，输入一个$64\times 64$的patch做训练，一次就能够计算N个点对应的梯度。（注意采样N个点的过程中采用了stratified sampling以避免clustering，这个stratified sampling是分层采样，本文不进行讲解）

4. HQ-SSL——认为N2V效率不够高

本文是2019 NeurIPS的论文：High-Quality Self-Supervised Deep Image Denoising，作者认为N2V存在的问题是：N2V将输入的一部分pixel进行屏蔽，也只有这一部分pixel才能对loss进行贡献，作者认为这样会相对降低训练效率。本文本质上还是盲点网络派系BSNs的思想。

在4.1中，我们先阐述HQ-SSL的架构，以及作者认为他们比N2V更优的原因，并在4.2中阐述此架构的实际实现。在4.3中简单回顾本工作中盲点思想的体现。最后在4.4讲述一些公式，阐明本工作如何利用所设计的架构进行训练和去噪。

4.1. HQ-SSL的理论架构

主要是对卷积和下采样的改进，下面详细阐述。

4.1.1. 对卷积的改进

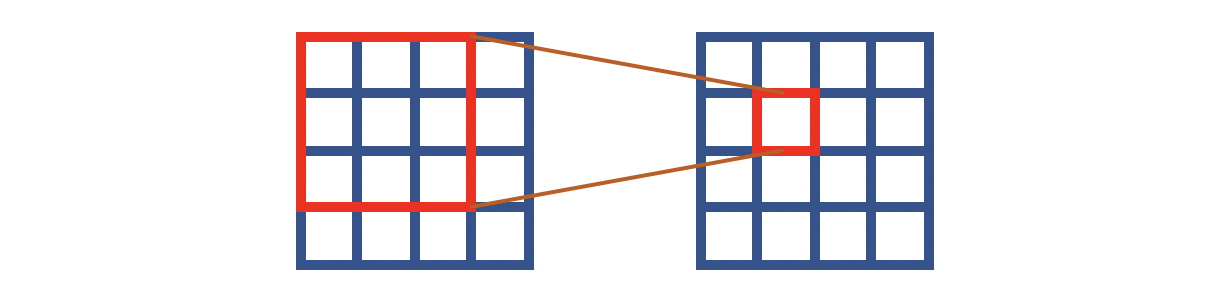
传统的卷积如上图所示，这里假设是$3\times 3$大小的卷积。注意输入和输出的对应关系：输出像素是输入对应感受野的中心位置。这就意味着网络推测一个像素，实际上用的是所有相邻位置+自身位置的像素。在N2V中，我们已经见识了盲点的思想，即像素的推测靠的是所有相邻位置的像素，但不包含自身位置的像素。如果将这种思想转换为卷积操作，姑且可以认为等价于下图的形式：

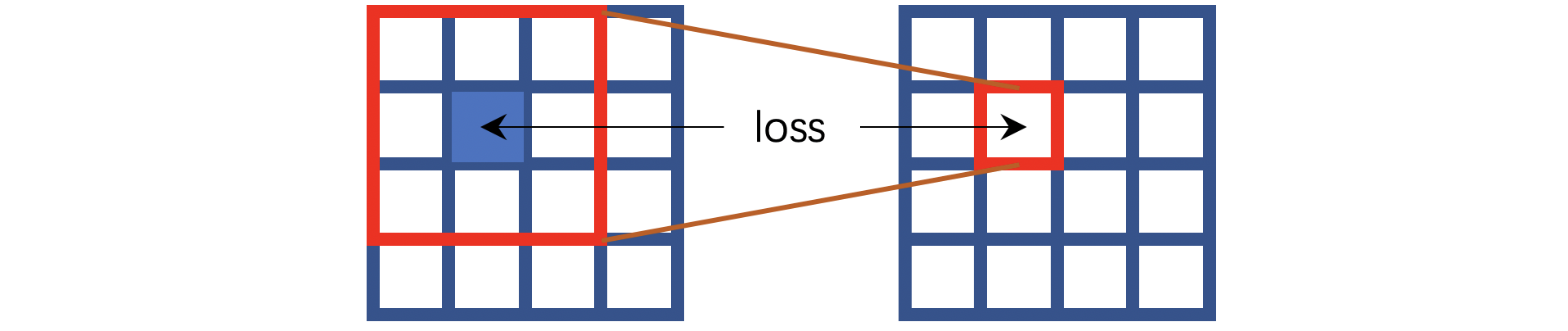
我用蓝色表示这个像素点是不可见的，也就是说卷积操作是无法看见中心像素点的。但是要求这样的计算能够推测中心位置的像素。这就是HQ-SSL的中心思想，不过这个工作并没有按照上图那样操作，它将卷积操作改造成了如下的方式：

HQ-SSL将卷积操作分为了四个方向，上图对应的是其中一种方向——输出像素取决于对应输入像素的上方相邻像素。如果算上所有四个方向，那么输出像素就取决于对应输入像素的上方、左方、下方、右方的若干相邻像素。

⚠️注意作者的思路是：N2V工作中的盲点本质上是让模型根据周围的像素点推测中心像素点，那么我们可以改造卷积操作，让每一次卷积运算都只能看见中心位置像素的若干相邻像素。

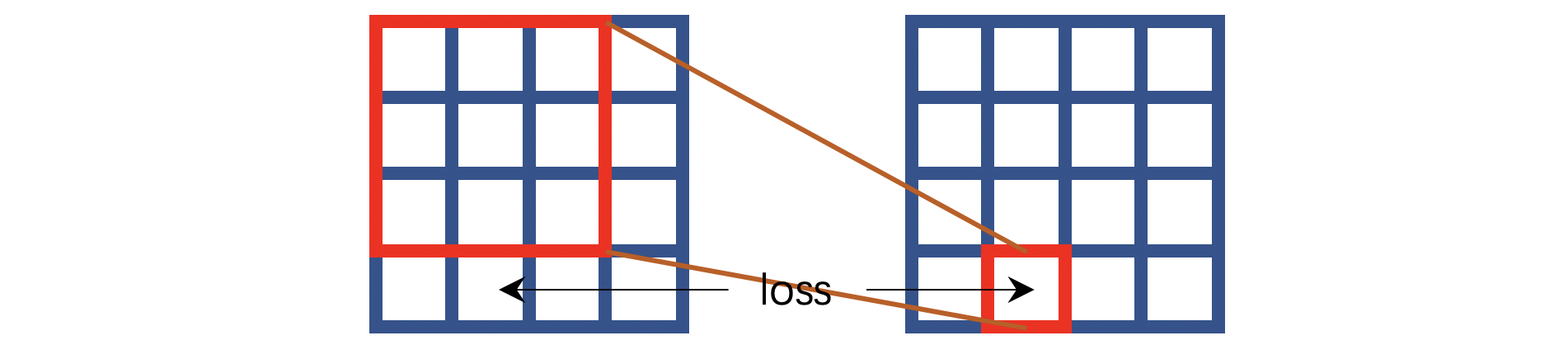
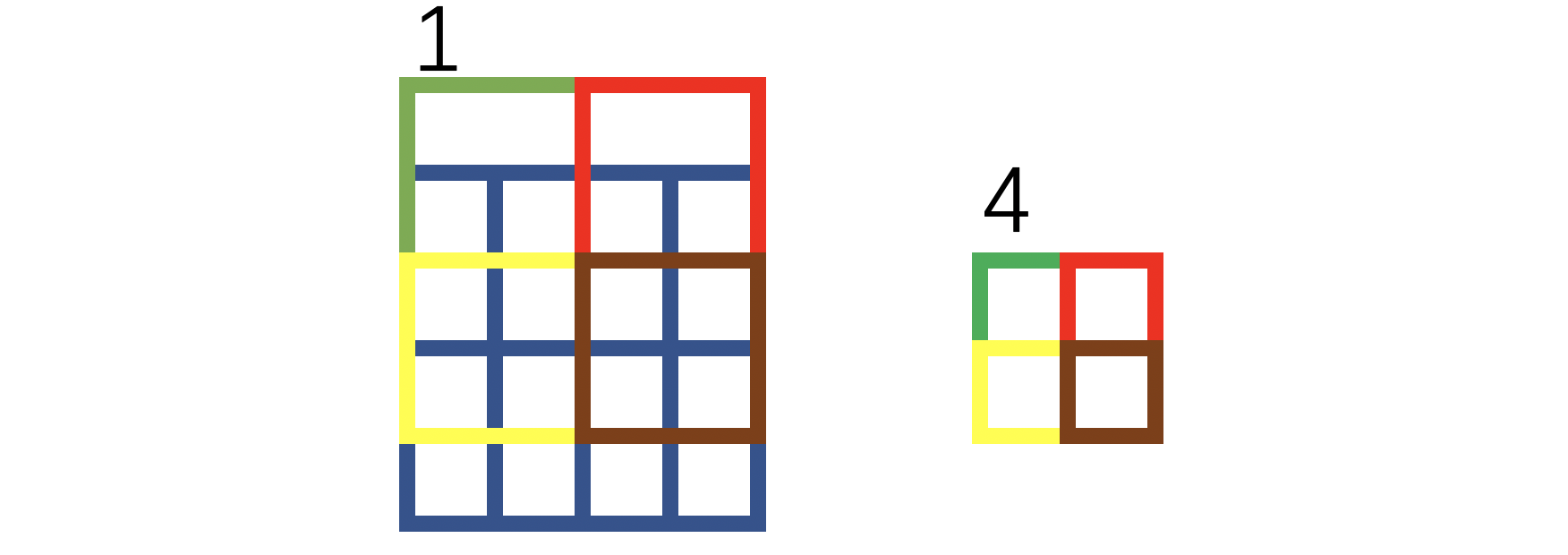
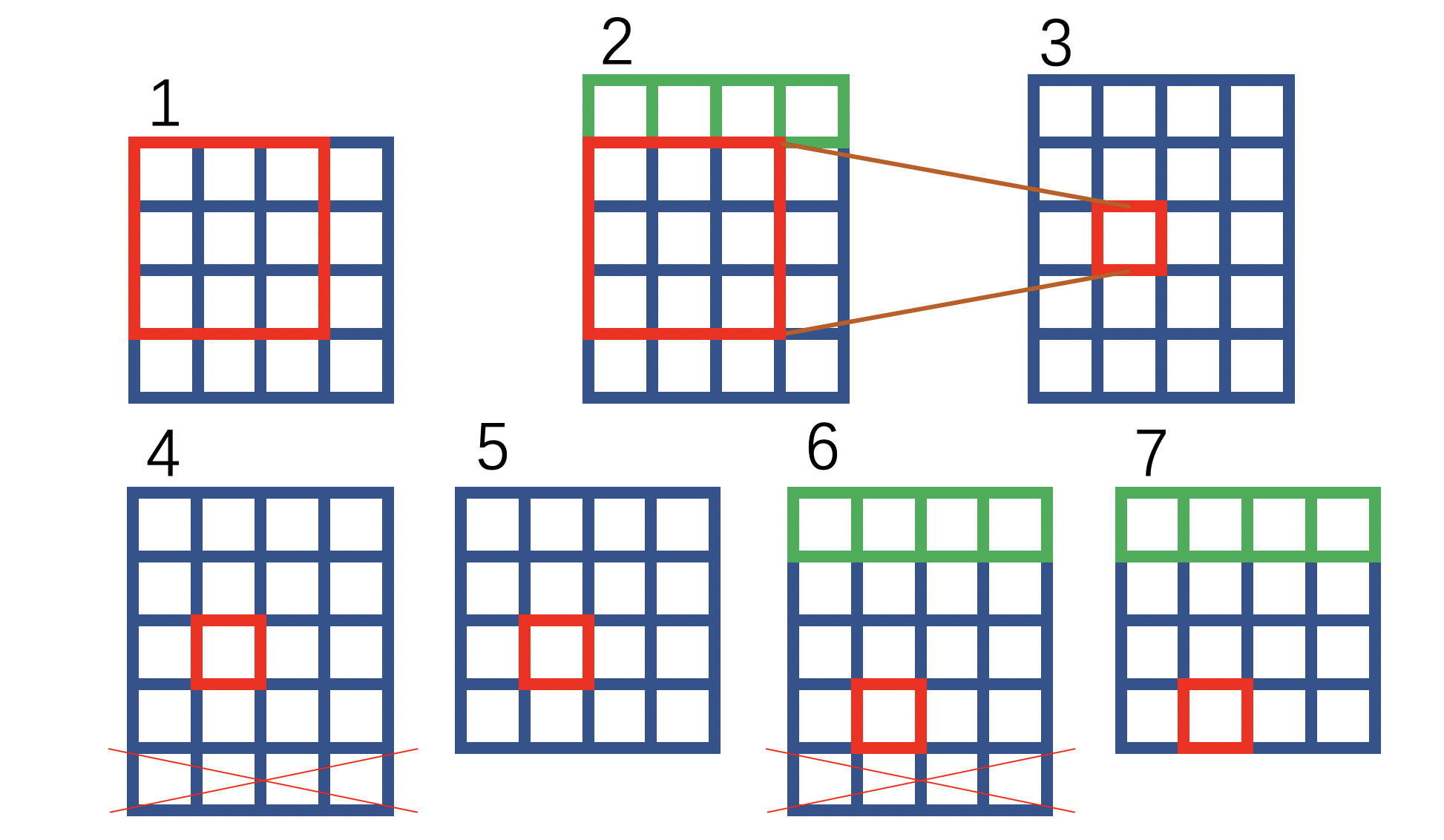
⭐️在实现上，作者采用的是$平移+补0+裁剪$的操作，用下图简单阐述：

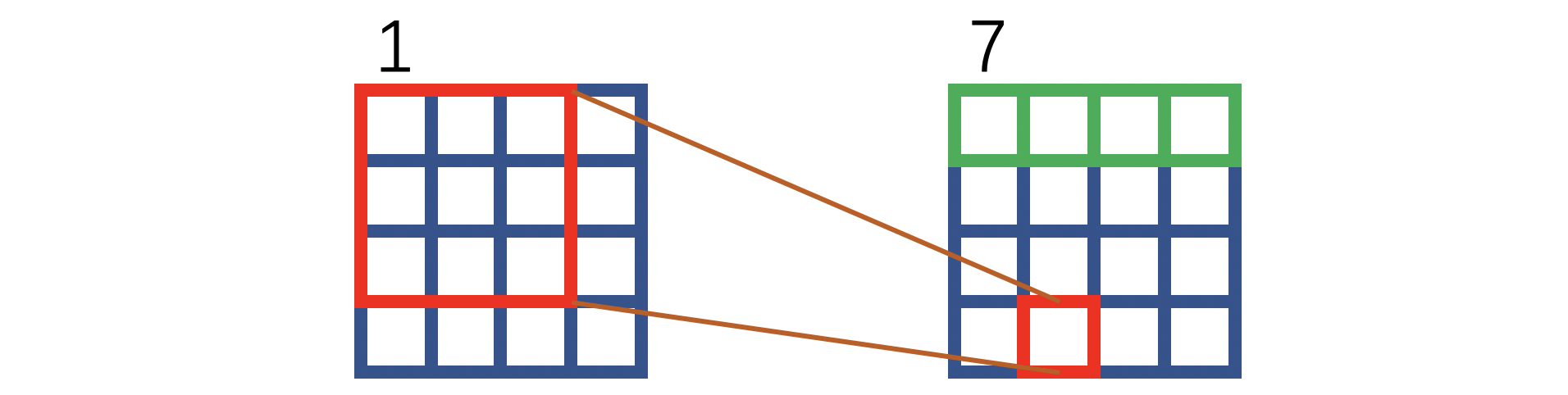
绿色表示补零操作，红色叉叉表示裁剪。可以看到，如上图操作之后，1和7的对应位置关系等价于上文所述HQ-SSL对卷积操作的改进方式：

注意：上述内容是根据作者提供的源代码获知，如果读者需要使用HQ-SSL，可以直接使用官方提供的代码。2023 CVPR有一篇工作引用了HQ-SSL，其官方代码和HQ-SSL的代码在卷积操作上是一致的。之所以写这段话，是因为HQ-SSL个人认为文章的关键段落较为晦涩，看不懂的读者朋友可以考虑直接看官方的代码，写的还是很易懂的。

⚠️注意：上述内容的补零和裁剪可以视为平移，上图仅平移了1个像素，是因为卷积核大小是$3\times 3$。如果是更大的卷积核，那么可以考虑不同的平移像素数量。

4.1.2. 对下采样的改进

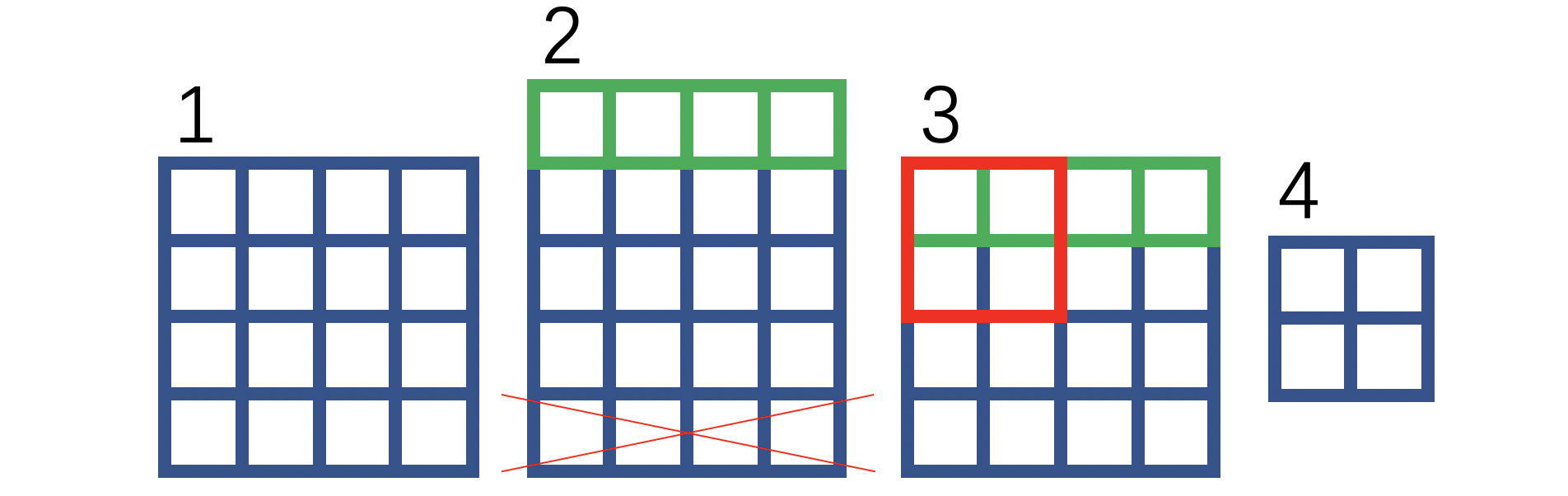
如果采用传统的$2\times 2$下采样，那么在上采样后，$2\times 2$区域内的四个像素，分别将和对应输入的同位置区域的四个像素相关联。作者针对下采样才用了和对卷积一样的改进方案——$平移+裁剪$：

绿色方框表示补0，红色叉叉表示裁剪。我们将1和4放到下图，并用不同的颜色，这样可以直观理解：

通过上图你可以认为下采样也有一个感受野，每个像素的感受野对应于该像素的位置以及该像素位置的上方位置。

和卷积一样，下采样也会对应四个方向。下采样的方向和卷积的方向是一致的。

注意上采样没有被改造。

4.1.3. 比N2V好在哪？

这里我就直接摘录原文的内容了：

N2V是将输入的一部分pixel进行屏蔽，只有这部分pixel才能对loss做贡献，或者只有这部分pixel才是loss的组成部分。作者认为这样会降低训练效率，所以采用HQ-SSL的设计思想，通过对卷积和下采样进行改造，可以等价出盲点网络BSN的效果。而且，由于仅仅改变了卷积和下采样，所有pixel都是loss的组成部分，或者说所有pixel都能对loss做贡献、对训练做贡献。

4.2. HQ-SSL的实际实现

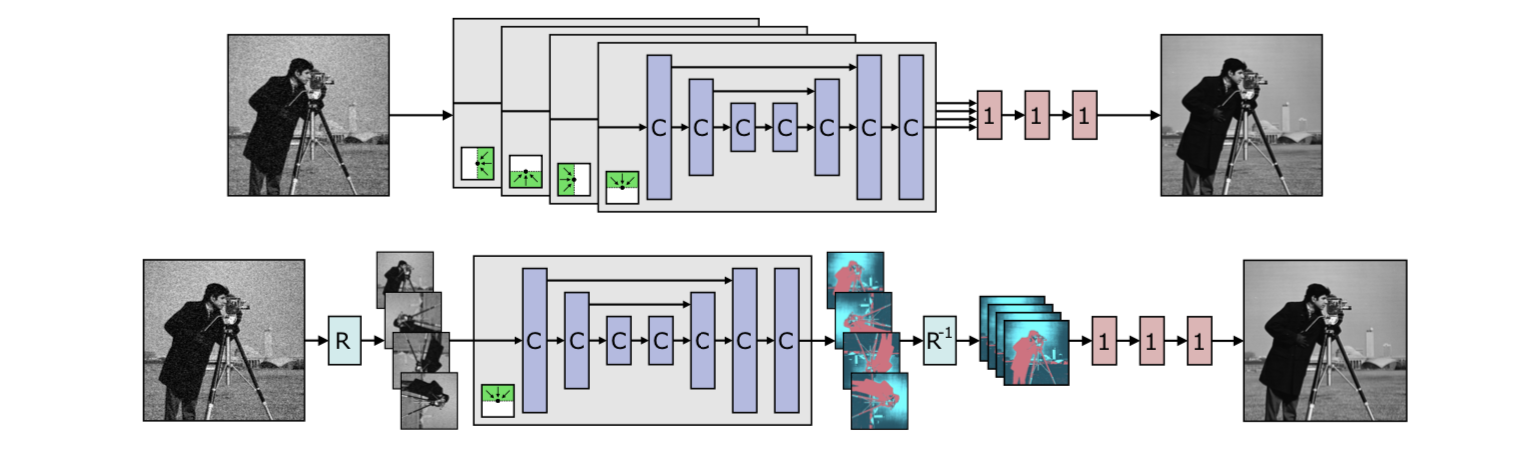
先看上图的上半部分，拥有4个branch。C表示4.1中所讲述的改造后的卷积，1表示$1\times 1$的卷积。绿色的部分表示四个方向的感受野，对应四个方向的卷积和下采样。再看上图的下半部分，表示作者实际的实现方式，虽然只有一个branch，但是通过旋转操作（图中的R）等价出了四个方向的卷积和下采样。由于只有一个branch，显然网络的参数量被大幅减少。

补：HQ-SSL的训练和测试须知

⭐️如果没有此部分内容，我们会根据对N2V的印象认为HQ-SSL的训练方式是：将上图右端的预测结果和左边的输入做loss，并以此训练。在测试阶段则是直接将noisy image输入网络，就能够获得对应的去噪结果。

实际上不是，在论文的第三节（3 Self-supervised Bayesian denoising with blind-spot networks），作者对训练和测试过程进行了阐述。摘录网上博客对此部分的分析（我没有深究这地方）：

网络输出噪声的一些分布参数，利用预测的参数可以进行去噪。

具体内容我不太感兴趣，所以不深究了。我阅读这篇论文主要目的是学习它的盲点思想。后续也有2023 CVPR的文章Spatially Adaptive Self-Supervised Learning for Real-World Image Denoising采用了HQ-SSL的盲点网络的设计（下一篇博客我将讲述它，届时我会将链接放在这里）。