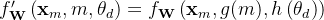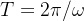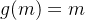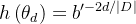前言
下半年以来,我全力推动我司大模型项目团队的组建,我虽兼管整个项目团队,但为了并行多个项目,最终分成了三个项目组,每个项目都有一个项目负责人,分别为霍哥、阿荀、朝阳
- 在今年Q4,我司第一项目组的第一个项目「AIGC模特生成平台」得到CSDN蒋总的大力支持,并亮相于CSDN举办的1024程序员节,一上来就吸引了很多市里领导、媒体、观众的关注,如今该平台的入口链接已在七月官网右上角
- 而第二项目组的论文审稿GPT,我和阿荀则一直全程推动整个流程的开发(第一版详见此文的第三部分、第二版详见:七月论文审稿GPT第2版:从Meta Nougat、GPT4审稿到Mistral、LongLora Llama)
到12月中旬,进入了模型训练阶段,选型的时候最开始关注的两个模型,一个Mistral 7B,一个Llama-LongLora,但考虑到前者的上下文长度是8K,面对一些论文时可能长度还是不够,于是我们便考虑让Mistral结合下YaRN
所以本文重点介绍下YaRN,顺带把位置编码外推ALiBi、线性插值等相关的方法一并总结下 - 至于第三项目组的知识库问答项目则也一直在并行推进,核心还是一系列各种细节问题的优化,而这个优化过程还是比较费时的
YaRN本质上是一种新的RoPE扩展方法(至于RoPE详见此文),可以比较高效的扩展大模型的上下文窗口,本文的写就基于YaRN论文:YaRN: Efficient Context Window Extension of Large Language Models,且为方便大家更好的理解本文,特地提前列下本文重要的几个参考文献(当下文出现带中括号的[6]、[7]、[9]时,便特指的以下相关文献)
-
[6] bloc97. NTK-Aware Scaled RoPE allows LLaMA models to have extended (8k+) context size without any fine-tuning and minimal perplexity degradation., 2023.
URL https://www.reddit.com/r/LocalLLaMA/comments/14lz7j5/ntkaware_ scaled_rope_allows_llama_models_to_have/
提出了NTK-Aware插值 -
[7] bloc97. Add NTK-Aware interpolation "by parts" correction, 2023. URL https://github.com/jquesnelle/scaled-rope/pull/1.
提出了 “NTK-by-parts”插值 -
[9] S. Chen, S. Wong, L. Chen, and Y. Tian. Extending context window of large language models via positional interpolation, 2023. arXiv: 2306.15595.
该研究团队来自Meta,该篇论文提出了 位置内插PI
有何问题 欢迎随时留言评论,thanks
第一部分 背景知识:从进制表示谈到直接外推、线性内插、进制转换
1.1 从进制表示到直接外推
注,本部分内容援引自苏剑林博客中的部分内容,为更易懂,我在其基础上做了一定的修改、解读
1.1.1 进制表示
假设我们有一个1000以内(不包含1000)的整数
- 最朴素的想法是直接作为一维浮点向量输入,然而0~999这涉及到近千的跨度,对基于梯度的优化器来说并不容易优化得动。那缩放到0~1之间呢?也不大好,因为此时相邻的差距从1变成了0.001,模型和优化器都不容易分辨相邻的数字
- 进一步,对于一个整数,比如759,这是一个10进制的三位数,每位数字是0~9。既然我们自己都是用10进制来表示数字的,为什么不直接将10进制表示直接输入模型呢?也就是说,我们将整数n以一个三维向量[a,b,c]来输入,a,b,c分别是n的百位、十位、个位
至于如果想要进一步缩小数字的跨度,我们还可以进一步缩小进制的基数,如使用8进制、6进制甚至2进制,代价是进一步增加输入的维度
1.1.2 直接外推
苏剑林说,假设我们还是用三维10进制表示训练了模型,模型效果还不错。然后突然来了个新需求,将n上限增加到2000以内,那么该如何处理呢?
如果还是用10进制表示的向量输入到模型,那么此时的输入就是一个四维向量了。然而,原本的模型是针对三维向量设计和训练的,所以新增一个维度后,模型就无法处理了。可能有读者想说,为什么不能提前预留好足够多的维度呢?
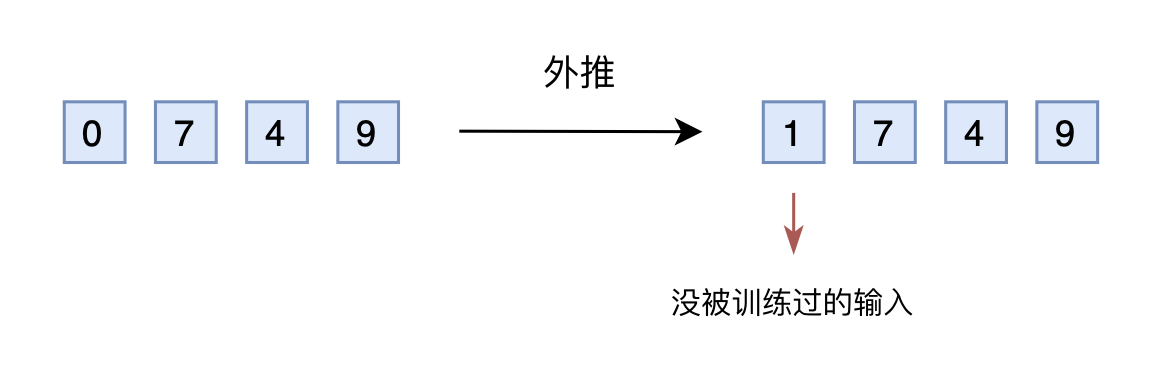
没错,是可以提前预留多几维,训练阶段设为0,推理阶段直接改为其他数字,这就是外推(Extrapolation)
然而,训练阶段预留的维度一直是0,如果推理阶段改为其他数字,效果不见得会好,因为模型对没被训练过的情况不一定具有适应能力。也就是说,由于某些维度的训练数据不充分,所以直接进行外推通常会导致模型的性能严重下降。
1.2 从线性内插到进制转换
1.2.1 线性内插
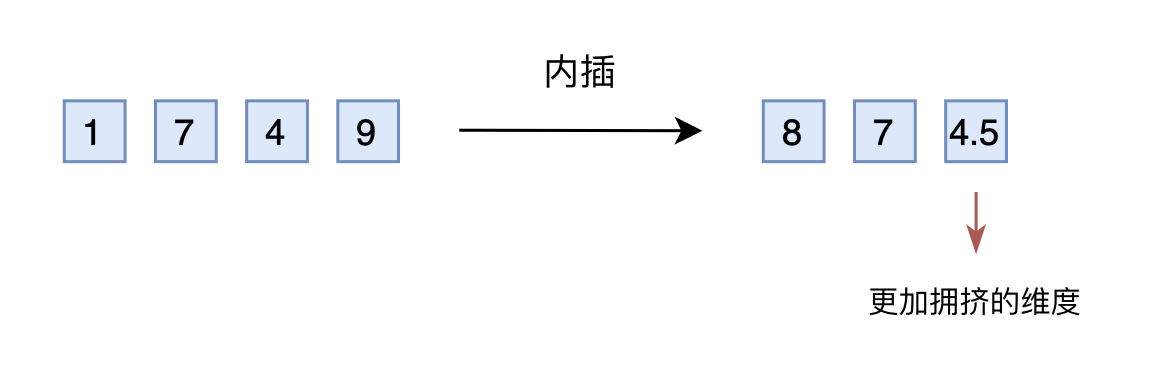
于是,有人想到了将外推改为内插(Interpolation),简单来说就是将2000以内压缩到1000以内
- 比如通过除以2,1749就变成了874.5,然后转为三维向量[8,7,4.5]输入到原来的模型中
从绝对数值来看,新的[7,4,9]实际上对应的是1498,是原本对应的2倍,映射方式不一致;
从相对数值来看,原本相邻数字的差距为1,现在是0.5,最后一个维度更加“拥挤” - 所以,做了内插修改后,通常都需要微调训练,以便模型重新适应拥挤的映射关系
当然,有读者会说外推方案也可以微调。是的,但内插方案微调所需要的步数要少得多
- 因为很多场景(比如位置编码)下,相对大小(或许说序信息)更加重要,换句话说模型只需要知道874.5比874大就行了,不需要知道它实际代表什么多大的数字。而原本模型已经学会了875比874大,加之模型本身有一定的泛化能力,所以再多学一个874.5比874大不会太难
- 不过,内插方案也不尽完美,当处理范围进一步增大时,相邻差异则更小,并且这个相邻差异变小集中在个位数,剩下的百位、十位,还是保留了相邻差异为1
换句话说,内插方法使得不同维度的分布情况不一样,每个维度变得不对等起来,模型进一步学习难度也更大
1.2.2 进制转换
有没有不用新增维度,又能保持相邻差距的方案呢?有,那就是进制转换
- 三个数字的10进制编码可以表示0~999
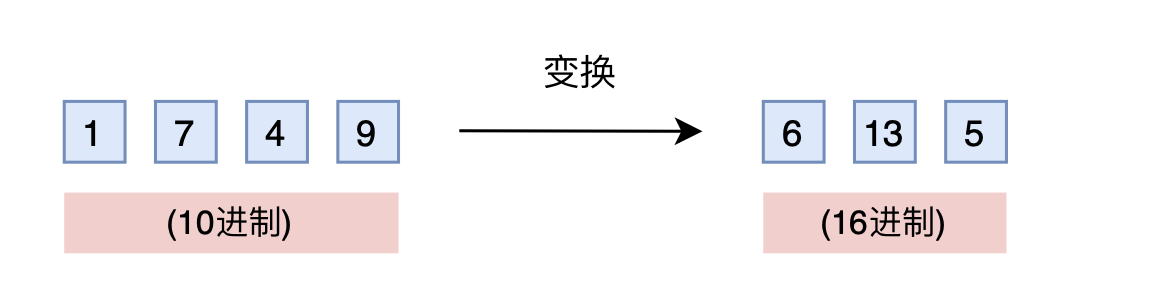
- 如果是16进制呢?它最大可以表示
所以,只需要转到16进制,如1749变为(咋计算得来的?很简单,1749不断除以16,并记录下每次的余数,
,这些余数从最后一个到第一个组成了1749的十六进制表示,即“6 13 5”),那么三维向量就可以覆盖目标范围,代价是每个维度的数字从0~9变为0~15
刚才说到,我们关心的场景主要利用序信息
- 原来训练好的模型已经学会了
,而在16进制下同样有
,比较规则是一模一样的
- 唯一担心的是每个维度超过9之后(10~15)模型还能不能正常比较,但事实上一般模型也有一定的泛化能力,所以每个维度稍微往外推一些是没问题的。所以,这个转换进制的思路,甚至可能不微调原来模型也有效
另外,为了进一步缩窄外推范围,我们还可以换用更小的![\lceil\sqrt[3]{2000} \mid=13](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNsY2VpbCU1Q3NxcnQlNUIzJTVEJTdCMjAwMCU3RCUyMCU1Q21pZCUzRDEz)
第二部分 从RoPE、直接外推到位置内插Position Interpolation
基于transformer的大型语言模型已经成为许多NLP任务的首选模型,其远程能力(如上下文学习(ICL))至关重要。在执行NLP任务时,其上下文窗口的最大长度一直是预训练LLM的主要限制之一。故,是否能够通过少量的微调(或不进行微调)来动态扩展上下文窗口已经变得越来越受关注。为此,transformer的位置编码是经常讨论的核心焦点问题
- 最初的Transformer架构使用了绝对正弦位置编码,后来被改进为可学习的绝对位置编码[Convolutional sequence to sequence learning]。此后,相对位置编码方案[Self-attention with relative position representations]进一步提升了transformer的性能
目前,最流行的相对位置编码是T5 relative Bias[Exploring the limits of transfer learning with a unified text-to-text transformer]、RoPE[34]、XPos[35]和ALiBi[Attention with linear biases enables input length extrapolation] - 位置编码的一个反复出现的限制是无法对「训练期间看到的上下文窗口之外的情况」进行泛化
One reoccurring limitation with positional encodings is the inability to generalize past the context window seen during training
虽然ALiBi等一些方法能够进行有限的泛化,但没有一种方法能够泛化到明显长于预训练长度的序列 - 好在已经有一些工作正在尝试克服这种限制。比如位置插值(Position Interpolation, PI)[Extending context window of large language models via positional interpolation]通过对RoPE进行轻微修改,并对少量数据进行微调,从而扩展上下文长度
- 作为一种替代方案,Reddit一网友bloc97通过该帖子,提出了“NTK-aware”插值方法[NTK-Aware Scaled RoPE allows LLaMA models to have extended(8k+) context size without any fine-tuning and minimal perplexity degradation],该方法考虑到高频信号的损失
此后,对“NTK感知”插值提出了两项改进
- 无需微调的预训练模型的“动态NTK”插值方法[14]
- 在对少量较长的上下文数据进行微调时表现最佳的“NTK-by-parts”插值方法[7]
“NTK感知”插值和“Dynamic NTK”插值已经在开源模型中出现,如Code Llama[31](使用“NTK感知”插值)和Qwen 7B[2](使用“动态NTK”)
2.1 旋转位置嵌入
2.1.1 RoPE的快速回顾
YaRN的基础是[RoFormer: Enhanced transformer with rotary position embedding]中介绍的旋转位置嵌入(RoPE)
RoPE是理解本文的重要基础,但考虑到本博客内已有另一篇文章详细阐述了位置编码与RoPE,所以如果你对本节有任何疑问,可进一步参考此文《一文通透位置编码:从标准位置编码、欧拉公式到旋转位置编码RoPE、ALiBi》
所以下面只参照YaRN论文做个最简单的回顾
- 首先,我们在一个隐藏层上工作,隐藏神经元的集合用
表示。给定向量序列
,遵循RoPE的表示法,注意力层首先将向量转换为查询向量和关键向量:
- 接下来,注意力权重被计算为
其中、
被认为是列向量,因此
就是简单的欧氏内积。在RoPE中,我们首先假设
是偶数,并将嵌入空间和隐藏状态识别为complex vector spaces
其中内积转化为
的实部「where the inner product q T k becomes the real part of the standard Hermitian inner product Re(q ∗k),如对该点有疑问的,请参见此文的3.2.1节」,更具体地说,同构将实数部分和复数部分交织在一起(the isomorphisms interleave the real part and the complex part)
- 为了将嵌入
、
转换为查询向量和键向量,我们首先给出了R-linear算子
在复坐标中,函数,
分别由以下的式子计算得到
这样做的好处是,查询向量和关键向量之间的点积只取决于如下所示的相对距离
在实坐标中,RoPE可以用下面的函数来表示
如此,便有
2.1.2 位置 的旋转位置编码(RoPE),本质上就是数字
的旋转位置编码(RoPE),本质上就是数字 的
的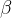 进制编码
进制编码
首先,如苏剑林所说,位置

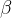
- 为了理解这一点,我们首先回忆一个10进制的数字
,我们想要求它的
进制表示的(从右往左数)第
位数字,方法是根据下面的公式计算得到(记为公式1)
也就是先除以
以上咋推导得来的呢?为方便大家一目了然,我再解释下
例如,让我们找到十进制数12345中从右边数的第三位的数字,相当于
,
(因为是十进制),
(因为要找的是第三位)
- 按照公式,我们首先计算
- 然后,我们计算
除以
,即
- 接下来,我们取这个结果的向下取整值,也就是去掉小数部分,得到
- 最后,我们对
取模,得到
所以,12345的从右边数的第三位数字是3
其次,苏剑林在其博客中再说道
- RoPE的构造基础是Sinusoidal位置编码,可以改写为下面的公式(记为公式2)
其中,
可能有的读者还是有点问题,可能还是得再解释下
首先,我们通过上文已多次提到的此文《一文通透位置编码:从标准位置编码、欧拉公式到旋转位置编码RoPE、ALiBi》,来回顾下transformer原始论文中的Sinusoidal位置编码
如阿荀所说,可知
其中
的取值范围为
,啥意思?意味着
所以,也就有了上面的公式2
pos
(0 2 4等偶数维用sin函数计算)公式2中 的指数项
0 0 1 0 2 1 3 1 4 2 5 2 6 .... 510 511
![\left[\cos \left(\frac{n}{\beta^{0}}\right), \sin \left(\frac{n}{\beta^{0}}\right), \cos \left(\frac{n}{\beta^{1}}\right), \sin \left(\frac{n}{\beta^{1}}\right), \cdots, \cos \left(\frac{n}{\beta^{d/2 -1}}\right), \sin \left(\frac{n}{\beta^{d/2 -1}}\right)\right]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNsZWZ0JTVCJTVDY29zJTIwJTVDbGVmdCUyOCU1Q2ZyYWMlN0JuJTdEJTdCJTVDYmV0YSU1RSU3QjAlN0QlN0QlNUNyaWdodCUyOSUyQyUyMCU1Q3NpbiUyMCU1Q2xlZnQlMjglNUNmcmFjJTdCbiU3RCU3QiU1Q2JldGElNUUlN0IwJTdEJTdEJTVDcmlnaHQlMjklMkMlMjAlNUNjb3MlMjAlNUNsZWZ0JTI4JTVDZnJhYyU3Qm4lN0QlN0IlNUNiZXRhJTVFJTdCMSU3RCU3RCU1Q3JpZ2h0JTI5JTJDJTIwJTVDc2luJTIwJTVDbGVmdCUyOCU1Q2ZyYWMlN0JuJTdEJTdCJTVDYmV0YSU1RSU3QjElN0QlN0QlNUNyaWdodCUyOSUyQyUyMCU1Q2Nkb3RzJTJDJTIwJTVDY29zJTIwJTVDbGVmdCUyOCU1Q2ZyYWMlN0JuJTdEJTdCJTVDYmV0YSU1RSU3QmQvMiUyMC0xJTdEJTdEJTVDcmlnaHQlMjklMkMlMjAlNUNzaW4lMjAlNUNsZWZ0JTI4JTVDZnJhYyU3Qm4lN0QlN0IlNUNiZXRhJTVFJTdCZC8yJTIwLTElN0QlN0QlNUNyaWdodCUyOSU1Q3JpZ2h0JTVE)
现在,对比公式1、公式2,是不是也有一模一样的
至于模运算,它的最重要特性是周期性,而公式2的cos、sin是不是刚好也是周期函数?所以,除掉取整函数这个无关紧要的差异外,RoPE(或者说Sinusoidal位置编码)其实就是数字
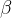
// 待更
2.2 直接外推之ALiBi
此文《一文通透位置编码:从标准位置编码、欧拉公式到旋转位置编码RoPE、ALiBi》的第4部分已经详细介绍过了ALiBi
简言之,ALiBi是对Transformers进行长度外推,即在短上下文窗口上进行训练,并在较长的上下文窗口上进行推理
- 好处是虽然一开始不用对模型结构做任何更改
- 但坏处是直接把位置外推到没有见到的地方会导致模型灾难性的崩坏(例如体现在PPL陡增),为了弥补,需要再做一些微调
// 待更..
2.3 位置内插:基于Positional Interpolation扩大模型的上下文窗口
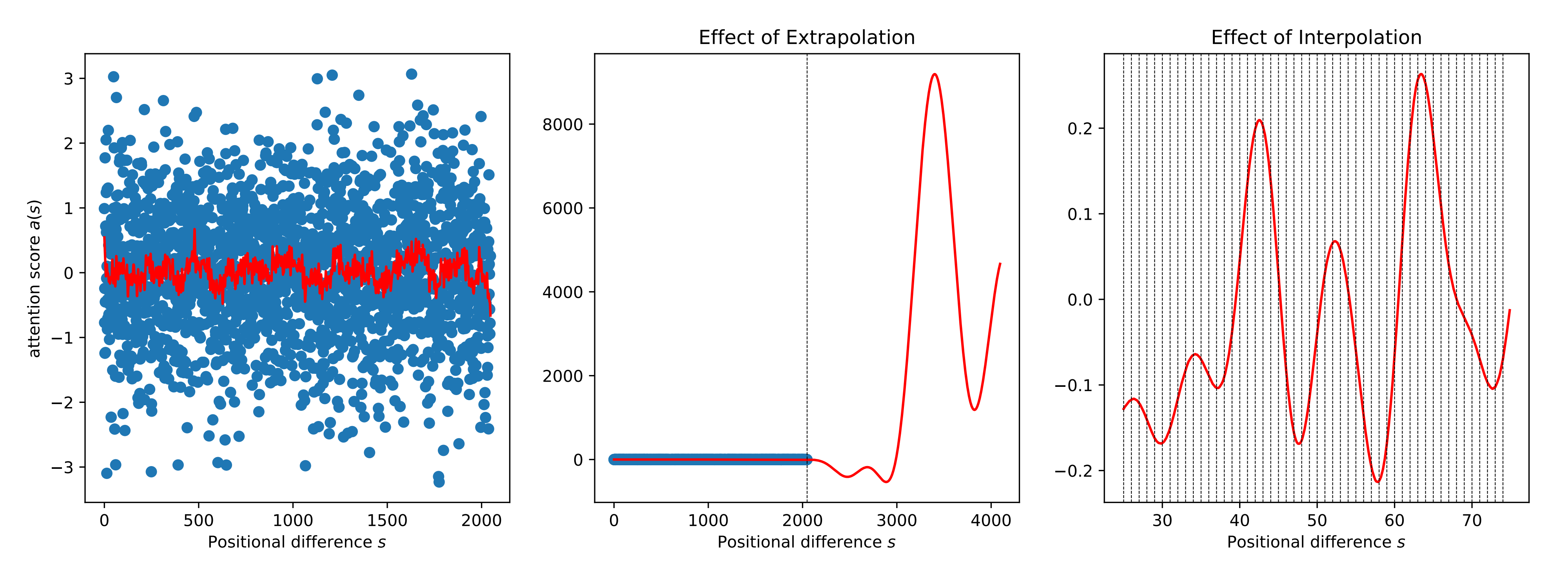
2.3.1 RoPE的问题:直接外推会出现比较大的Attention Score
再次回顾一下RoPE
给定位置索引
![\mathbf{x}:=\left[x_{0}, x_{1}, \ldots, x_{d-1}\right]^{\top}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNtYXRoYmYlN0J4JTdEJTNBJTNEJTVDbGVmdCU1QnhfJTdCMCU3RCUyQyUyMHhfJTdCMSU3RCUyQyUyMCU1Q2xkb3RzJTJDJTIweF8lN0JkLTElN0QlNUNyaWdodCU1RCU1RSU3QiU1Q3RvcCU3RA%3D%3D)
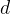
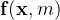
其中
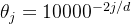
把这个自注意得分的公式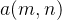
可知,这个自注意力得分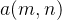
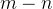
虽然RoPE的上界确实随着 |m − n|的减小而衰减,但上界仍然可能相当大(即上界可能严重依赖于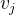
实际上,如果我们将所有三角函数视为基函数(即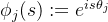
其中 
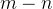
是依赖于
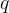
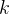
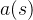
根本原因在于三角函数族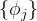
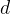
因此,对于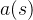
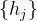
2.3.2 什么是位置内插Positional Interpolation
由于语言模型通常是用固定的上下文长度进行预训练的,自然会问如何通过在相对较少的数据量上进行微调来扩展上下文长度
对于使用RoPE作为位置嵌入的语言模型,Chen等人[9]和kaiokendev[21]同时提出了位置插值(position Interpolation, PI),将上下文长度扩展到预训练极限之外,对于后者Super-HOT kaiokendev(2023)的工作,它在RoPE中插入了位置编码,将上下文窗口从2K扩展到8K
对于前者Chen等人的工作,按照该篇论文《Extending context window of large language models via positional interpolation》,可知
- 关键思想是,我们不是进行外推,而是直接将位置索引缩小(不是插值位置嵌入,而是插值位置索引,这对于RoPE等位置编码更合适,并且可能需要较少的训练,因为没有添加可训练参数,即Instead of interpolating position embeddings, our method interpolates position indices, which is more suitable for RoPE like position encodings and may require less training since no trainable parameters are added),使最大位置索引与预训练阶段的先前上下文窗口限制相匹配(we directly down-scale the position indices so that the maximum position index matches the previous context window limit in the pre-training stage)
至于理论依据就是可以在相邻的整数位置上插值位置编码,毕竟位置编码可以应用在非整数的位置上
we interpolate the position encodings at neighboring integer positions,utilizing the fact that position encodings can be applied on non-integer positions
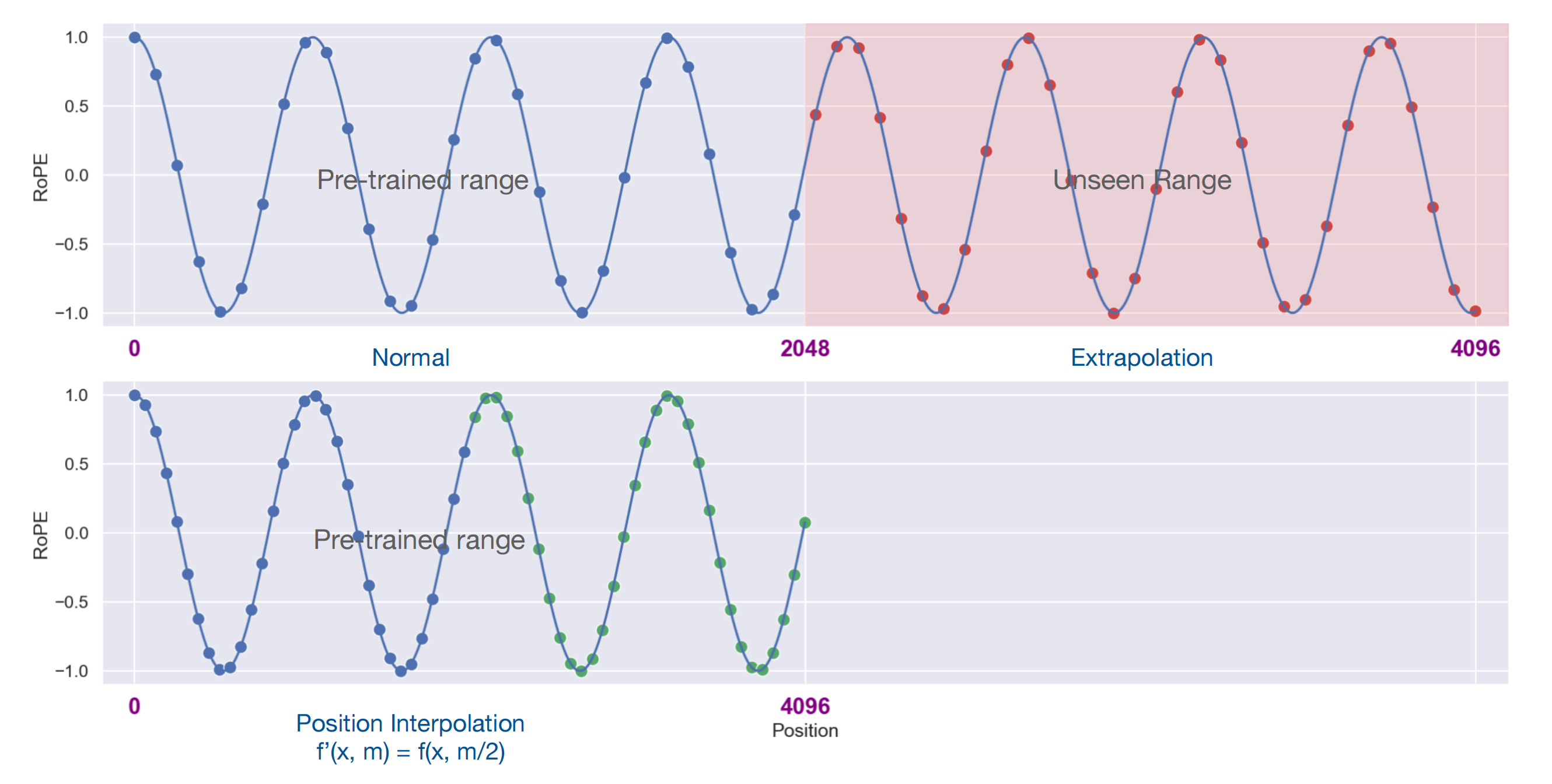
如下图所示,下图左上角为预训练阶段的位置向量范围[0,2048],右上角为长度外推的部分(2048,4096]
如果直接使用位置(2048,4096]进行推理,那么因为模型没有见过这一部分的位置,效果会出现灾难性的下降。那么,就把[0,4096]这个区间”压缩“到[0,2048]不就可以了嘛
于是,原先的1就变成了0.5,4096就变成了2048,这就是位置内插法,即把没见过的位置映射到见过的位置 - 相当于对于绝对位置
,我们把它”缩放“一下,变成
。其中,
为原先支持的长度(如2048),
为需要扩展的长度(如4096)。这样,在计算query和key的时候,就有
其中是超出预训练限制的新上下文窗口
- 考虑到扩展的上下文长度与原始上下文长度之间的比例一直特别重要,我们以此定义
有了这个定义(这个
其实本质上即指位置内插需要扩大的倍数),我们便可以将公式
重写并简化为以下一般形式(其中
,
):
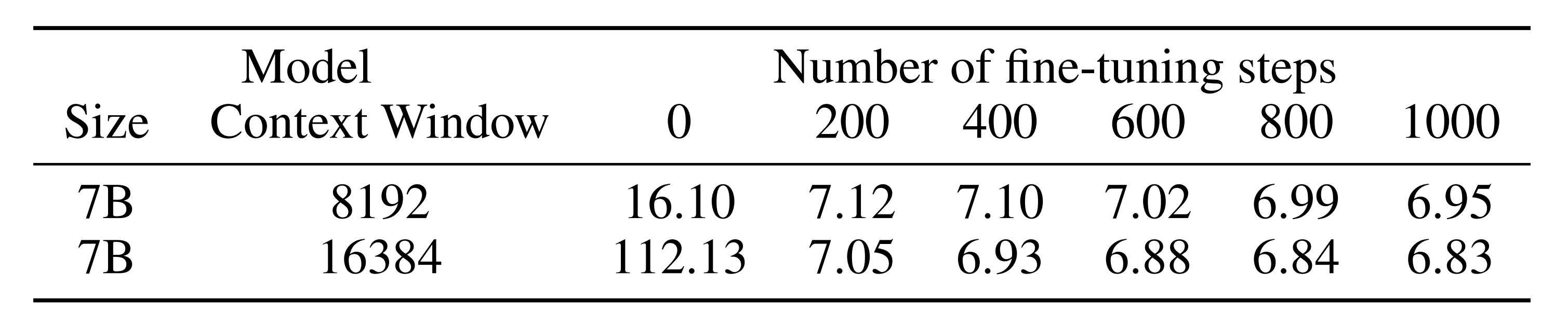
- 最终,通过位置插值方法,将预训练的7B、13B、33B和65B LLaMA模型(Touvron等人,2023)扩展到大小为32768的各种上下文窗口,只需要在Pile(是个书籍语料库)等数据集上上进行1000步的微调即可获得良好的质量(Position Interpolation can easily enable very long context windows (e.g. 32768), requiring only fine-tuning for 1000 steps on the Pile (Gao et al., 2020) to achieve a good quality),这与预训练成本相比,微调的成本可以忽略不计
且微调过程只需要数万到数十万个示例,微调的结果对示例的选择不敏感。 原因在于模型在微调阶段仅适应新的上下文窗口,从良好的初始化开始,而不是获取新的知识
(We also find that the result of the fine-tuning is not sensitive to the choice of examples. The reason may be that the model is only adapting to the new context window during the fine-tuning phase, starting from a good initialization, as opposed to acquiring new knowledge)总之,PI除了重新缩放使用位置插值扩展的模型的位置索引外,没有以任何方式修改LLaMA模型架构(包括其中的自注意力机制,从而减轻了上下文窗口扩展对注意力分数计算的影响)
那PI之后,是否一定要微调呢?也不一定,只是效果有所区别而已,具体而言
- PI之后,在没有微调的情况下(在步骤0),模型可以展示出一定的语言建模能力,如扩展到8192上下文窗口的困惑度<20所示(相比之下,直接外推方法导致困惑度>
)
- PI之后,经过微调,困惑度迅速改善。 在200步时,模型超过了2048上下文窗口大小的原始模型困惑度,表明模型能够有效地使用比预训练设置更长的序列进行语言建模。 在1000步时,我们可以看到模型稳步改善,并取得了显著更好的困惑
此外,PI也比直接微调的效果更好,相比之下,仅通过直接微调扩展的LLaMA模型仅将有效上下文窗口大小 kmax从2048增加到2560,即使经过10000多步的微调也没有明显加速窗口大小的增长迹
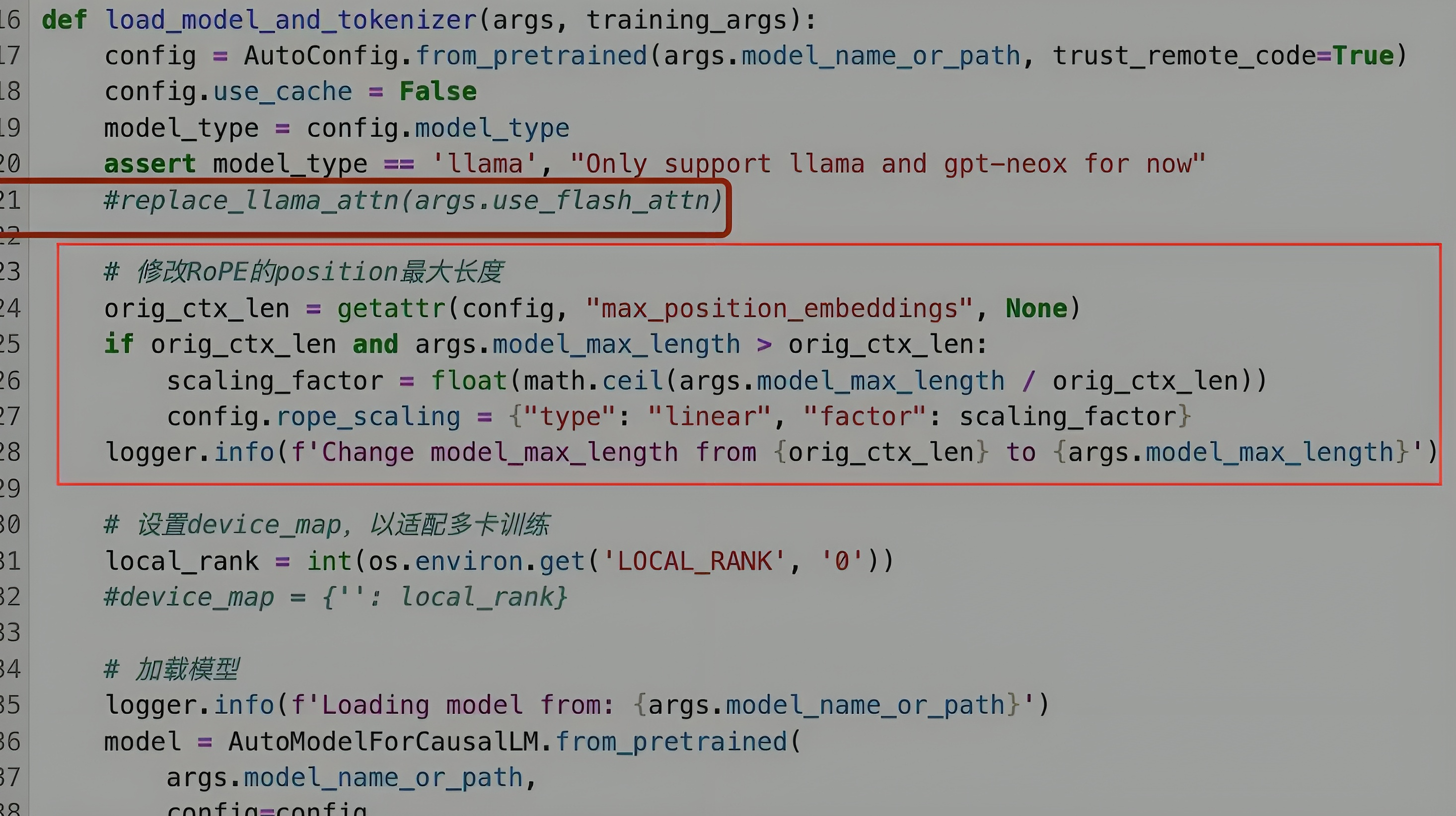
以下是我司在通过PI微调llama 3时(更多详见:一文速览Llama 3及其微调:如何通过paper-review数据集微调Llama3 8B)
- 直接用的longlora的代码「至于什么是longlora,请参见此文:《从LongLoRA到LongQLoRA(含源码剖析):大模型上下文长度的超强扩展》」
- 因为longlora的代码实现了PI + S2-attn,故把S2-attn相关的部分注释掉后,即相当于通过PI微调llama 3了
2.3.3 位置内插的问题
话说,位置插值法有什么问题呢?
- 我们先看下三角函数
,它的周期是
对应到RoPE里的每个维度,其中
(其中,
是指位置,
是指维度)
- 计算得到周期为:
,其中,用
表示base,即10000
从周期计算的公式我们可以知道,针对不同的维度编码,每个维度对应的三角函数周期是越来越大的(即对应到低频、高频)
如果插值是针对绝对位置,那么对每个维度
都同等地生效;但是周期小(高频)维度,插值之后会变得很密集(本来一个周期包含10个值,但是内插之后能包含20个值),这样高频的维度就变的很拥挤
第三部分 从NTK-aware、NTK-by-parts到Dynamic NTK插值
3.1 “NTK-aware”插值:高频外推,低频内插
为了解决RoPE嵌入插值时丢失高频信息(losing high frequency information when interpolating the RoPE embeddings)的问题,Reddit一网友通过[NTK-Aware Scaled RoPE allows LLaMA models to have extended (8k+) context size without any fine-tuning and minimal perplexity degradation]开发了“NTK-aware”插值,核心思想是:高频外推,低频内插
- 我们不是将RoPE的每个维度平均缩放一个因子
,而是通过减少高频的缩小和增加低频的放大来将插值压力分散到多个维度(Instead of scaling every dimension of RoPE equally by a factor s, we spread out the interpolation pressure across multiple dimensions by scaling high frequencies less and low frequencies more)
- 虽然人们可以通过许多方法获得这样的变换,但最简单的方法是对θ的值进行基础更改(One can obtain such a transformation in many ways, but the simplest would be to perform a base change on the value of θ)
啥意思呢,其实我们是要把2.1.2节中的公式2
该公式2中的最低频项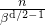

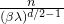


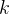
从而解得
而公式2中的最高频是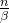

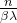
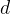

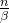
从而,NTK-aware便这样把外推和内插给结合起来了
YaRN论文中对“NTK-aware”的内插方案是如下表述的(虽和上面的表示一个本质,但符号和表述上有不同)
“NTK-aware”插值是对RoPE的修改,使用
和以下函数
且
其中
相当于上面的
,且
类似于上面的
,
相当于上面的
可能有同学有疑问了,咋和上面的表示不一致呢?
原因如阿荀所说
- 上面(进制角度)的
和这里(YaRN论文)的
才是一回事(容易把上面的
和这里的
混淆看做同一个)
- 且上面(进制角度)的计数范围是从0到d/2-1的,而这里(YaRN论文)的计数范围是从1到|D|/2的
与位置插值PI相比,该方法在扩展非微调模型的上下文大小方面表现得更好
- 然而,这种方法的一个主要缺点是,由于它不仅仅是一种插值方案,一些维度被轻微外推到“超出边界”的值,因此使用“NTK-aware”插值[6]进行微调的结果不如PI[9]
- 此外,由于存在“越界”值,理论尺度因子
并不能准确描述真实的上下文扩展尺度。在实践中,对于给定的上下文长度扩展,尺度值s必须设置得高于预期尺度
我们注意到,在本文发布前不久,Code Llama[31]发布了,并通过手动将基数b扩展到1M(使用“NTK-aware”扩展)
3.2 相对局部距离的损失-“NTK-by-parts”插值
在本节伊始,得先介绍一个概念,即波长,所谓波长,其描述的在维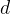
一般而言,把
定义为RoPE嵌入在第
隐维处的波长:
有一些插值方法(例如位置插值PI)不关心波长的维数,我们将这些方法称为“盲”插值方法(blind interpolation),比如像PI和“NTK-aware”插值这样的blind interpolation方法中,我们面对所有RoPE隐藏维度的没有做任何针对性的处理(因为它们对网络有相同的影响),而其他方法(如YaRN),我们将其归类为“有针对性的”插值方法
进一步,关于RoPE嵌入的一个有趣的观察是
- 给定上下文大小
,有一些维度
的波长长于预训练期间看到的最大上下文长度(
),这表明一些维度的嵌入可能在旋转域中不均匀分布(might not be distributed evenly in therotational domain)
在这种情况下,我们假设拥有所有唯一的位置对意味着绝对的位置信息保持完整(we presume having all unique position pairs implies that theabsolute positional information remains intact)
相反,当波长较短时,只有相对位置信息可以被网络访问(when the wavelength is short, onlyrelative positional information is accessible to the network) - 此外,当我们以
的比例或使用
的基数将RoPE的所有维度进行拉伸时,所有tokens都变得更接近彼此,因为两个向量的点积旋转较小的量更大(as the dot product of two vectors rotated by a lesser amountis bigger)
这种缩放严重损害了LLM理解其内部嵌入之间的小型和局部关系的能力。我们假设,这种压缩导致模型在邻近标记的位置顺序上被混淆,从而损害模型的能力
This scaling severely impairs a LLM’s ability to understand small and local relationshipsbetween its internal embeddings. We hypothesize that such compression leads to the model beingconfused on the positional order of close-by tokens, and consequently harming the model’s abilities.
为了解决上述问题,选择不插值更高频率的维度,而总是插值更低频率的维度(we choose not to interpolate the higher frequency dimensions at all while always interpolating the lower frequency dimensions)。特别是
- 如果波长
比上下文长度
小得多,此时不插值
- 如果波长
等于或大于上下文长度
,此时只做插值,不做任何外推(不像以前的“NTK-aware”方法)
- 两者之间的维度可以兼而有之(dimensions in-between can have a bit of both),类似于“NTK-aware”插值
因此,在原始上下文大小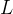

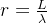
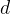

为了确定上述不同插值策略的边界,引入两个额外参数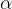
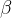
- 如果是
(比如
,意味着波长大于上下文长度),则将线性插入一个尺度
(完全像PI,避免任何外推)
- 至于如果是
则不插值
接下来,定义斜坡函数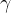
从而借助该函数,“NTK-by-parts”方法可以定义如下
“NTK-by-parts”插值是对RoPE的一种修改,基于以下函数
和
的值根据具体情况进行调整。当然,通过实验发现,对于Llama家族的模型而言,其中
和
的比较好的取值是
和
// 待更
3.3 "Dynamic NTK"插值
在很多用例中,以从1到最大上下文大小不等的序列长度进行多次前向传递。一个典型的例子是自回归生成,其中序列长度在每一步之后递增1
有两种方法可以应用使用比例因子
- 方法1:在整个推理周期中,嵌入层是固定的,包括缩放因子
,其中
是固定数量的扩展上下文大小
- 方法2:在每次前向传递中,位置嵌入更新缩放因子(the position embedding updates the scale factor):
,其中
是当前序列的序列长度
上述方法中,方法1的问题在于模型在长度小于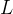

对此,故提出了方法2,我们称这种推理时间方法为动态缩放方法,当再与“NTK-aware”插值相结合时,我们称之为“动态NTK”插值
一个值得注意的事实是,“动态NTK”插值在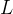

第四部分 YaRN全面解析
介绍完“NTK-aware”插值、“NTK-by-parts”插值、"Dynamic NTK"插值之后,接下来即将介绍YaRN(另一种RoPE扩展方法),这是一种改进的方法,可以有效地扩展使用旋转位置嵌入(RoPE)训练的模型的上下文窗口,包括LLaMA[38]、GPT-NeoX[5]和PaLM[10]家族的模型
4.1 YaRN怎么来的:基于“NTK-by-parts”插值修改注意力
除了前述的插值技术,我们还观察到,在对logits进行softmax操作之前引入温度t可以统一地影响困惑度,无论数据样本和扩展上下文窗口上的token位置如何,更准确地说,我们将注意力权重的计算修改为
通过将RoPE重新参数化为一组2D矩阵对,给实现注意力缩放带来了明显的好处(The reparametrization of RoPE as a set of 2D matrices has a clear benefit on the implementation of this attention scaling)
- 我们可以利用“长度缩放”技巧,简单地将复杂的RoPE嵌入按相同比例进行缩放,使得qm和kn都以常数因子
进行缩放
这样一来,在不修改代码的情况下,YaRN能够有效地改变注意力机制
we can instead use a "length scaling" trick which scales both qm and kn by a constant factor p 1/t by simply scaling the complex RoPE embeddings by the same amount.
With this, YaRN can effectively alter the attention mechanism without modifying its code. - 此外,在推理和训练期间,它没有额外开销,因为RoPE嵌入是提前生成并在所有向前传递中被重复使用的。结合“NTK-by-parts”插值方法,我们就得到了YaRN方法
Furthermore, it has zero overhead during both inference and training, as RoPE embeddings are generated in advance and are reused for all forward passes. Combining it with the "NTK-by-parts" interpolation, we have the YaRN method
对于LLaMA和LLaMA 2模型,我们推荐以下值:
上式是在未进行微调的LLaMA 7b、13b、33b和65b模型上,使用“NTK-by-parts”方法对各种因素的尺度扩展进行最小困惑度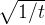
且相同的t值也适用于Llama 2模型(7b、13b和70b),这表明熵增加和温度常数t的性质可能具有一定的“普遍性”,并且可以推广到某些模型和训练数据中(It suggests that the property of increased entropy and the temperature constant t may have certain degree of "universality" and may be generalizable across some models and training data)
- YaRN方法在微调和非微调场景中均超过以前所有方法,由于其占用空间较小,YaRN与修改注意力机制库(如Flash Attention 2[13])直接兼容
- 且在对不到0.1%的原始预训练数据进行微调后,YaRN在上下文窗口扩展中达到了最先进的性能
同时,如果YaRN与动态缩放的推理技术相结合而得到的Dynamic-yarn,其允许在超过2倍的上下文窗口扩展,而无需任何微调
4.2 实际应用效果
// 待更
第五部分 LongLora所用的Shifted Sparse Attention(S2-Attn)
此部分独立成文为:从LongLoRA到LongQLoRA(含源码剖析):超长上下文大模型的高效微调方法
参考文献与推荐阅读
- 了解几种外推方案做了什么
https://zhuanlan.zhihu.com/p/647145964
https://zhuanlan.zhihu.com/p/642398400 - Transformer升级之路:7、长度外推性与局部注意力
- Transformer升级之路:10、RoPE是一种β进制编码
- 大语言模型结构之:RoPE位置外推
- 大模型上下文长度扩展的一篇综述文献
The What, Why, and How of Context Length Extension Techniques in Large Language Models -- A Detailed Survey - RoPE外推的缩放法则 —— 尝试外推RoPE至1M上下文
创作、修订、完善记录
- 12.19,开始写本文的前两部分
- 12.21,修订第二部分..
- 12.22,新增一节:“2.1.2 位置
的旋转位置编码(RoPE),本质上就是数字
的
进制编码”
且结合苏剑林的博文,补充说明:2.4.1 “NTK-aware”插值:高频外推,低频内插
另,开始写:2.4.2 相对局部距离的损失-“NTK-by-parts”插值,和第三部分 YaRN的全面解析 - 24年4.28,根据PI的论文多次优化本文2.3节的内容
- 4.29,新增第五部分的标题
第五部分 LongLora所用的Shifted Sparse Attention(S2-Attn) - 5.8,把原来属于「第二部分 从RoPE、直接外推、位置内插到NTK-aware/NTK-by-parts/Dynamic NTK插值」的内容拆成两部分,成为如今的
第二部分 从RoPE、直接外推到位置内插Position Interpolation
第三部分 从NTK-aware、NTK-by-parts到Dynamic NTK插值
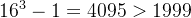
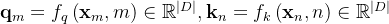
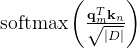
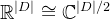
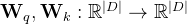
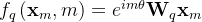
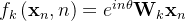
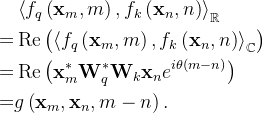
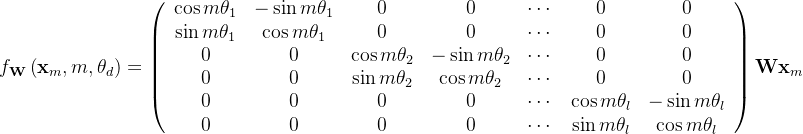
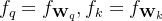
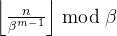

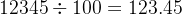
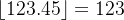
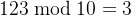

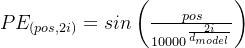
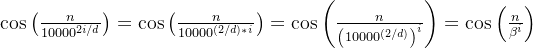









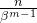
![\mathbf{f}(\mathbf{x}, m)=\left[\left(x_{0}+\mathrm{i} x_{1}\right) e^{\mathrm{i} m \theta_{0}},\left(x_{2}+\mathrm{i} x_{3}\right) e^{\mathrm{i} m \theta_{1}}, \ldots,\left(x_{d-2}+\mathrm{i} x_{d-1}\right) e^{\mathrm{i} m \theta_{d / 2-1}}\right]^{\top}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNtYXRoYmYlN0JmJTdEJTI4JTVDbWF0aGJmJTdCeCU3RCUyQyUyMG0lMjk%3D%3D%5Cleft%5B%5Cleft%28x_%7B0%7D+%5Cmathrm%7Bi%7D%20x_%7B1%7D%5Cright%29%20e%5E%7B%5Cmathrm%7Bi%7D%20m%20%5Ctheta_%7B0%7D%7D%2C%5Cleft%28x_%7B2%7D+%5Cmathrm%7Bi%7D%20x_%7B3%7D%5Cright%29%20e%5E%7B%5Cmathrm%7Bi%7D%20m%20%5Ctheta_%7B1%7D%7D%2C%20%5Cldots%2C%5Cleft%28x_%7Bd-2%7D+%5Cmathrm%7Bi%7D%20x_%7Bd-1%7D%5Cright%29%20e%5E%7B%5Cmathrm%7Bi%7D%20m%20%5Ctheta_%7Bd%20/%202-1%7D%7D%5Cright%5D%5E%7B%5Ctop%7D)
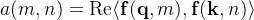
![a(s)=\operatorname{Re}\left[\sum_{j=0}^{d / 2-1} h_{j} e^{\mathrm{i} s \theta_{j}}\right]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9hJTI4cyUyOSUzRCU1Q29wZXJhdG9ybmFtZSU3QlJlJTdEJTVDbGVmdCU1QiU1Q3N1bV8lN0JqJTNEMCU3RCU1RSU3QmQlMjAvJTIwMi0xJTdEJTIwaF8lN0JqJTdEJTIwZSU1RSU3QiU1Q21hdGhybSU3QmklN0QlMjBzJTIwJTVDdGhldGFfJTdCaiU3RCU3RCU1Q3JpZ2h0JTVE)