混合专家模型（MoE）From Sparse to Soft Mixtures of Experts

先引用一个写的不错的帖子：混合专家模型（MoE）的概念介绍和应用案例_moe 大模型-CSDN博客

MoE是一种深度学习架构，它由多个专家网络（experts）和一个门控网络（gating network）组成。每个输入样本会被分配给一个或多个专家进行处理，而门控网络则决定每个专家对输入的贡献程度。

在《From Sparse to Soft Mixtures of Experts》这篇论文中，作者提出了一种将稀疏专家模型（Sparse Mixture of Experts, Sparse MoE）转变为软专家混合模型（Soft Mixture of Experts, Soft MoE）的算法。以下是算法实现的关键步骤和原理：

1. 稀疏专家模型概述

在稀疏专家模型中，每次只激活一部分专家，从而减少计算量。常见的方法是使用门控网络（Gating Network）来选择哪些专家被激活。这种方法的一个主要问题是梯度不连续和训练不稳定性。

2. 软专家混合模型的核心思想

软专家混合模型的核心思想是：在稀疏选择的基础上，每个专家的激活程度不再是0或1，而是一个连续的值。通过这种方式，所有专家都可以在一定程度上参与计算，从而提高模型的稳定性和性能。

3. 算法实现步骤

3.1 门控网络

门控网络接受输入特征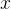，输出一个表示专家激活程度的向量 g(x) 。对于个专家，这个向量的长度也是。在稀疏模型中，向量 g(x) 是一个稀疏向量，大部分元素为0，只有少数元素为1。

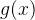
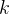
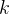
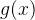
在软专家模型中，这个向量的元素是连续值，表示每个专家的激活权重。可以使用softmax函数将输出转化为概率分布：

g(x)=softmax(W_gx + b_g))

其中， W_g 和 b_g 是门控网络的参数。

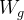
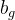
3.2 专家网络

每个专家网络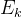 E_k 接受输入特征并输出预测值。软专家模型中，每个专家的输出 E_k 会被其激活权重 g_k(x) 加权：

$y=\sum^{K}_{k=1}g_k(x)E_k(x)$

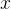
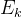
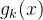
其中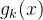， g_k(x) 是第个专家的激活权重， E_k(x) 是第个专家的输出。

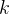
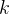
3.3 损失函数

损失函数通常是任务相关的标准损失（如交叉熵损失、均方误差等）。需要注意的是，由于软专家模型中所有专家都参与计算，因此可以对每个专家的梯度进行反向传播，确保模型的稳定性和收敛性。

4. 训练过程

软专家混合模型的训练过程与传统神经网络类似，主要包括前向传播、损失计算和反向传播。在训练过程中，通过优化算法（如SGD、Adam等）更新模型参数。

5. 实验和验证

论文通过实验验证了软专家混合模型的效果。实验表明，相对于稀疏专家模型，软专家混合模型在多个任务上表现更好，具有更高的稳定性和更好的收敛性。

伪代码示例

下面是一个简单的伪代码示例，展示了软专家混合模型的实现步骤：

import torch
import torch.nn as nn
import torch.optim as optim

class GatingNetwork(nn.Module):
    def __init__(self, input_dim, num_experts):
        super(GatingNetwork, self).__init__()
        self.fc = nn.Linear(input_dim, num_experts)
    
    def forward(self, x):
        return torch.softmax(self.fc(x), dim=-1)

class ExpertNetwork(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(ExpertNetwork, self).__init__()
        self.fc = nn.Linear(input_dim, output_dim)
    
    def forward(self, x):
        return self.fc(x)

class SoftMoE(nn.Module):
    def __init__(self, input_dim, output_dim, num_experts):
        super(SoftMoE, self).__init__()
        self.gating_network = GatingNetwork(input_dim, num_experts)
        self.expert_networks = nn.ModuleList([ExpertNetwork(input_dim, output_dim) for _ in range(num_experts)])
    
    def forward(self, x):
        gating_weights = self.gating_network(x)
        expert_outputs = torch.stack([expert(x) for expert in self.expert_networks], dim=1)
        output = torch.sum(gating_weights.unsqueeze(-1) * expert_outputs, dim=1)
        return output

# 示例训练代码
input_dim = 10
output_dim = 1
num_experts = 5
model = SoftMoE(input_dim, output_dim, num_experts)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 假设有训练数据 inputs 和 targets
inputs = torch.randn(32, input_dim)
targets = torch.randn(32, output_dim)

# 前向传播
outputs = model(inputs)
loss = criterion(outputs, targets)

# 反向传播和优化
optimizer.zero_grad()
loss.backward()
optimizer.step()

这个伪代码展示了一个简单的软专家混合模型的实现，包括门控网络、专家网络以及模型的前向传播、损失计算和训练过程。通过这种方式，可以实现稀疏专家模型向软专家混合模型的转变。

MOE（Mixture of Experts）模型在训练和推理阶段的工作方式确实有所不同。具体来说：

训练阶段：在训练过程中，MOE模型通常会激活所有的专家（experts）。这样做是为了让每个专家都有机会学习，并且能够更好地分工合作。每个专家的参数都会根据训练数据进行更新，从而使整个模型能够更好地拟合数据。
推理阶段：在推理阶段，MOE模型会选择性地激活一部分专家，而不是全部。这通常是通过一个门控机制（gating mechanism）来实现的。门控机制根据输入数据的特征，决定激活哪些专家。这样做的目的是提高计算效率，减少计算资源的消耗，同时保持较高的模型性能。这种选择性激活的机制使得MOE模型具有稀疏性，因此被称为稀疏MOE。

简而言之，在训练时所有的专家都参与，而在推理时则根据输入选择性地激活部分专家，从而实现稀疏性。

术语：

slots：

"slots"在这里指的是每个输入令牌可以分配给专家的槽位数量

在MoE模型中，改变“槽位数量”（即每个令牌分配给的专家数量）会影响模型的性能和效率。如果每个令牌分配的槽位太多，可能会导致模型过于复杂，难以训练。如果每个令牌分配的槽位太少，可能无法充分利用所有专家的专长。