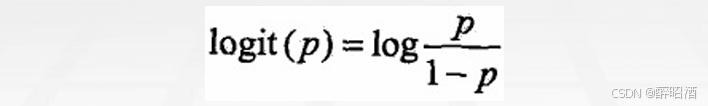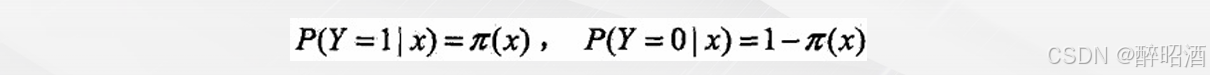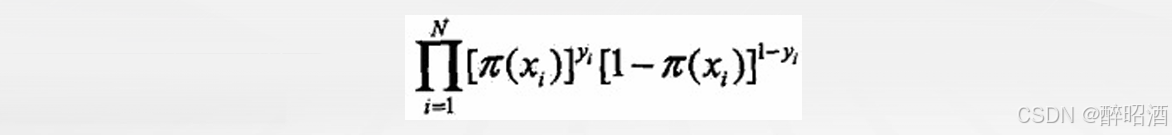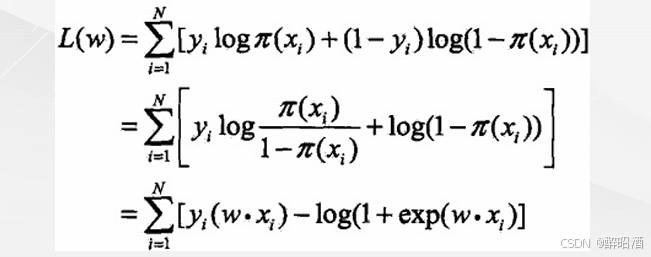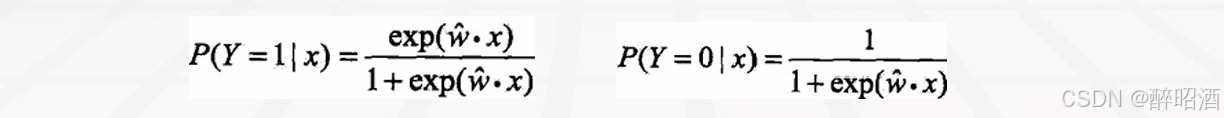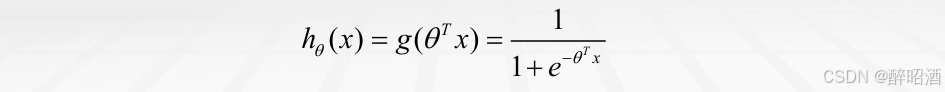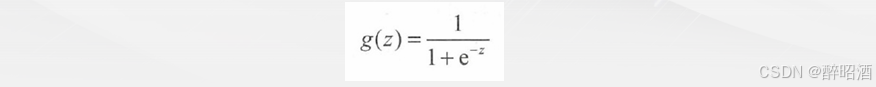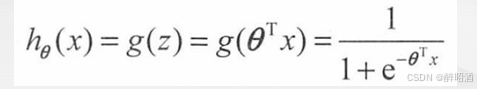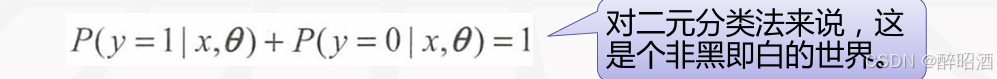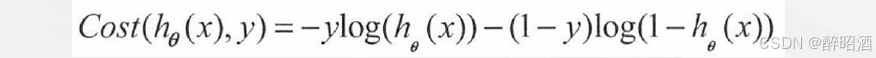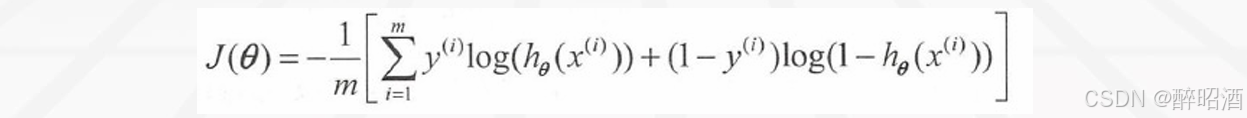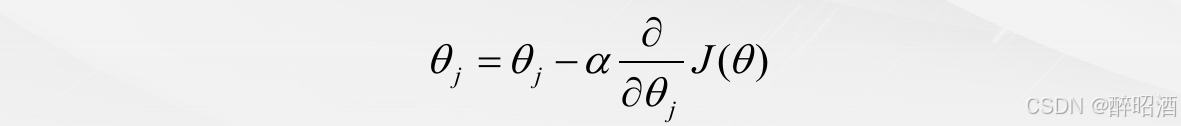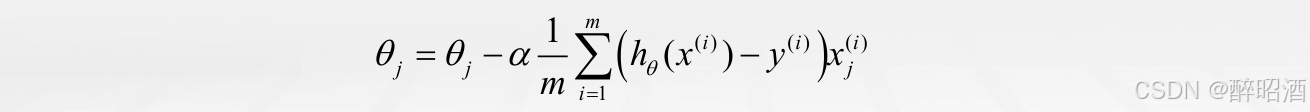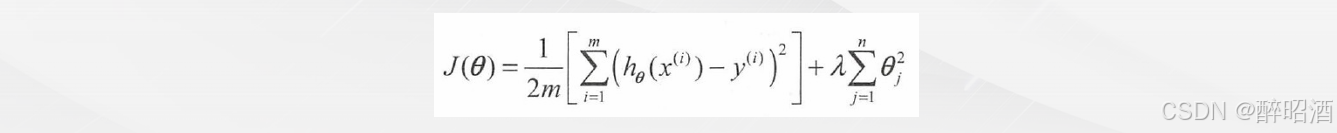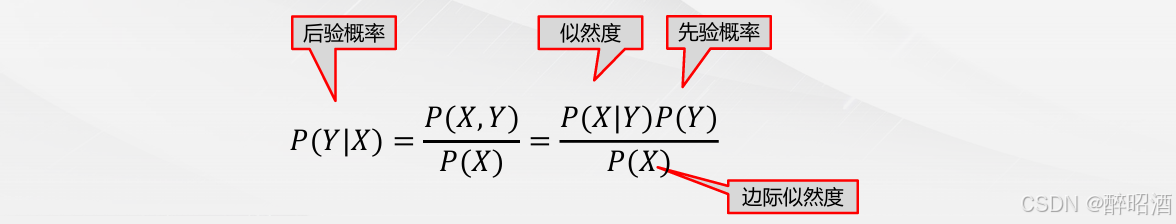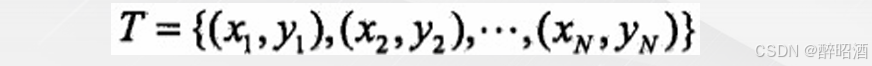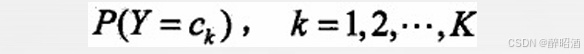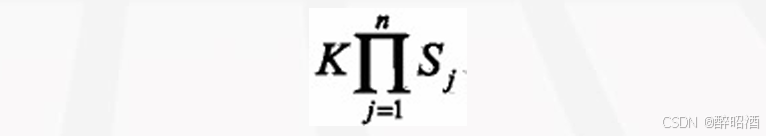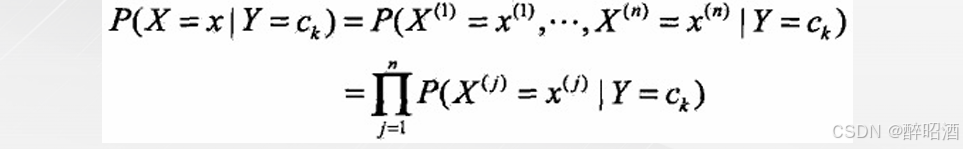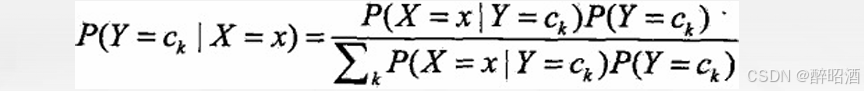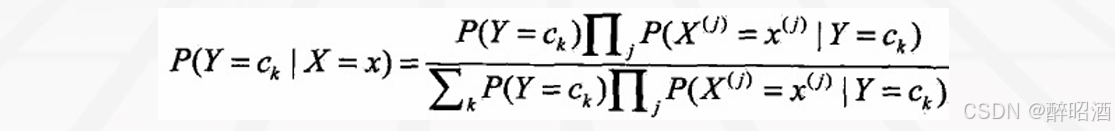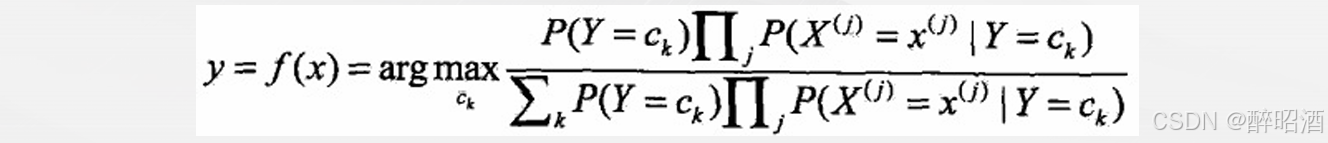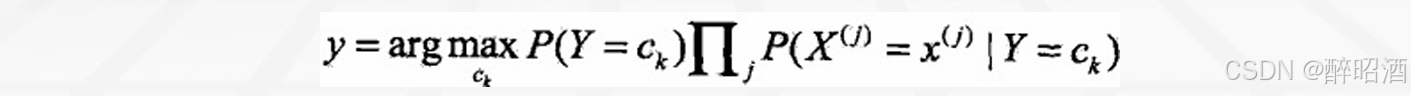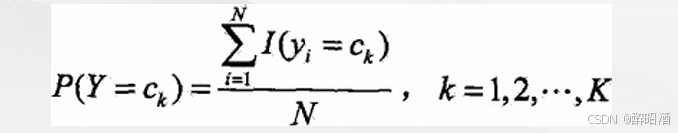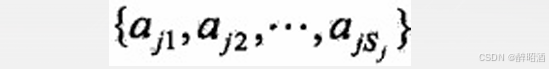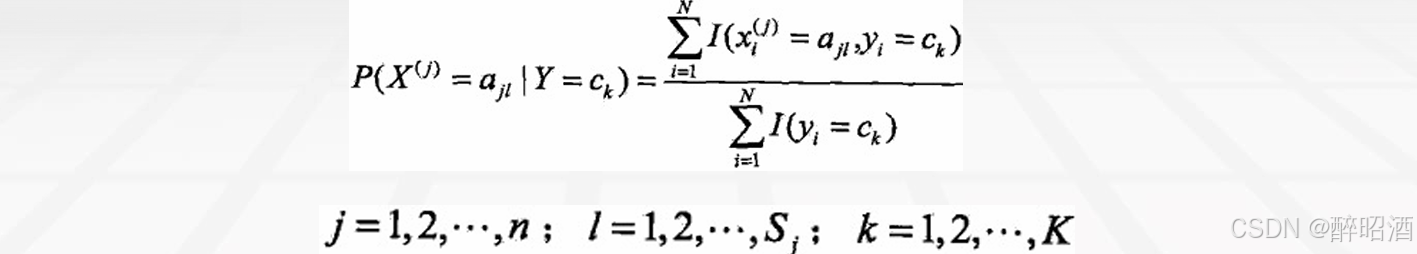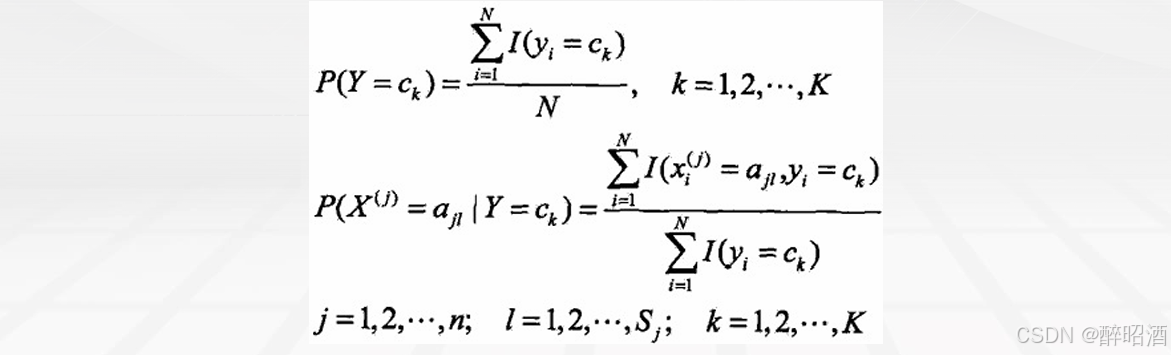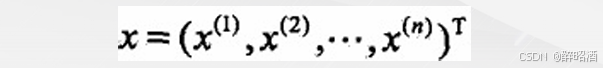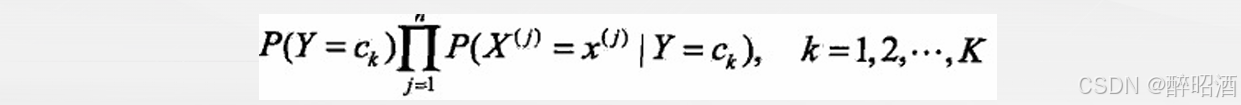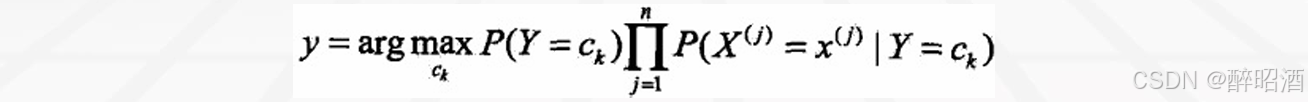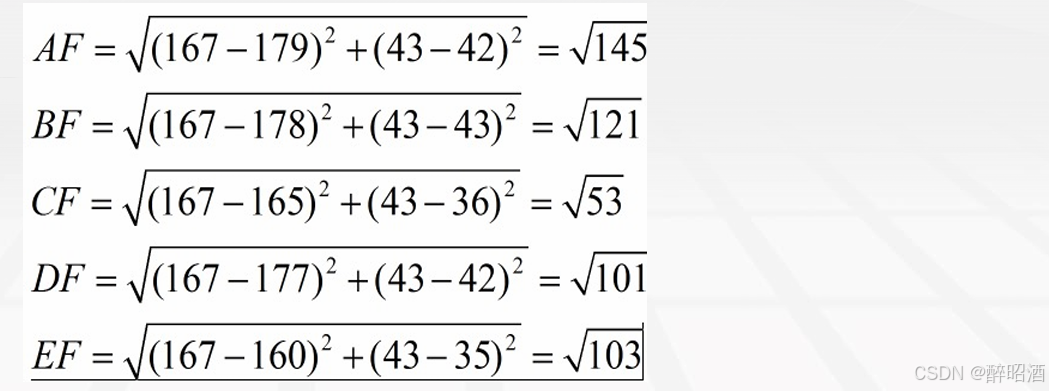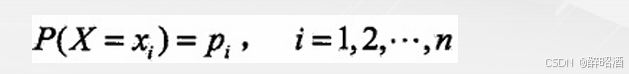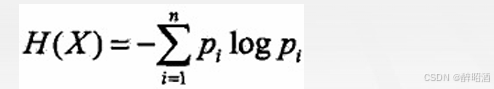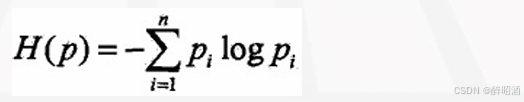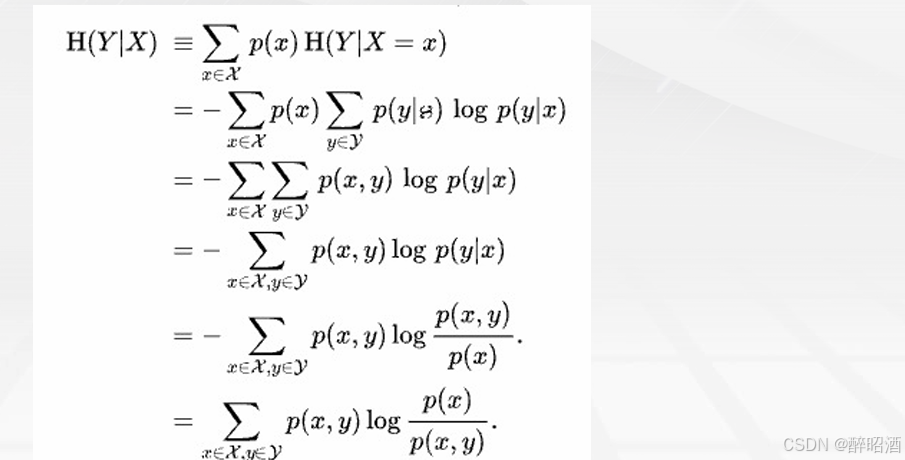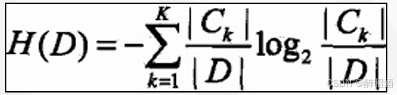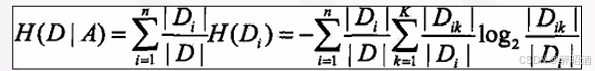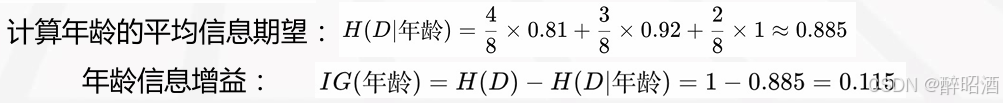一、逻辑回归

1.1逻辑回归

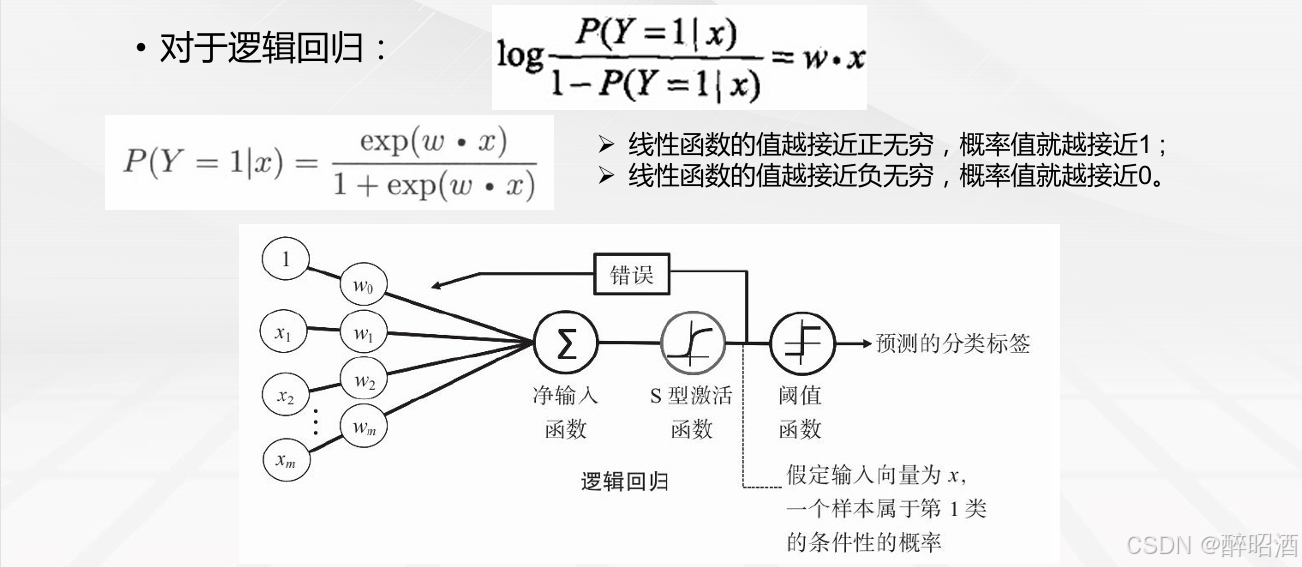
二项逻辑回归

• Binomial logistic regression model是一种分类模型

        • 由条件概率P(Y|X)表示的分类模型

        • 形式化为logistic distribution

        • X取实数，Y取值1,0

特点：

• 事件的几率odds：事件发生与事件不发生的概率之比为

• 称为事件的发生比(the odds of experiencing an event),

• 对数几率：

似然函数

• 那么对于上述i个观测事件，设

• 其联合分布函数，即似然函数为：

• 目标：求出使这一似然函数的值最大的参数估计，w1,w2,…,wn， 使得L(w)取得最大值。

• 对L(w)取对数：

模型参数估计

• 对数似然函数：

• 对L(w)求极大值，得到w的估计值。

• 通常采用梯度下降法及拟牛顿法，学到的模型：

多项logistic回归

• 设Y的取值集合为 ： {1，2，...，K}

• 多项logistic回归模型：

• 二项逻辑回归的参数估计法也可以推广到多项逻辑回归。

逻辑回归与线性回归联系和区别

• 联系：逻辑回归本质上还是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和，然后使用函数sigmoid函数g(z)将连续结果值映射到（0，1）之间，我们将线性回归模型的表达式代入到Logistic(Sigmoid)函数之中，就得到了逻辑回归的表达式：

• 区别：

①线性回归要求变量服从正态分布，logistic回归对变量分布没有要求。

②线性回归要求因变量是连续性数值变量，而logistic回归要求因变量是分类型变量。

③线性回归要求自变量和因变量呈线性关系，而logistic回归不要求自变量和因变量呈线性关系。

④logistic回归是分析因变量取某个值的概率与自变量的关系，而线性回归是直接分析因变量与自变量的关系。

logistic回归与线性回归实际上有很多相同之处，最大的区别就在于他们的因变量不同，其他的基本都差不多，正是因为如此，这两种回归可以归于同一个家族，即广义线性模型（generalized linear model）。

这一家族中的模型形式基本上都差不多，不同的就是因变量不同，

• 如果是连续的，就是多重线性回归，

• 如果是二项分布，就是logistic回归。

logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释。所以实际中最为常用的就是二分类的logistic回归。

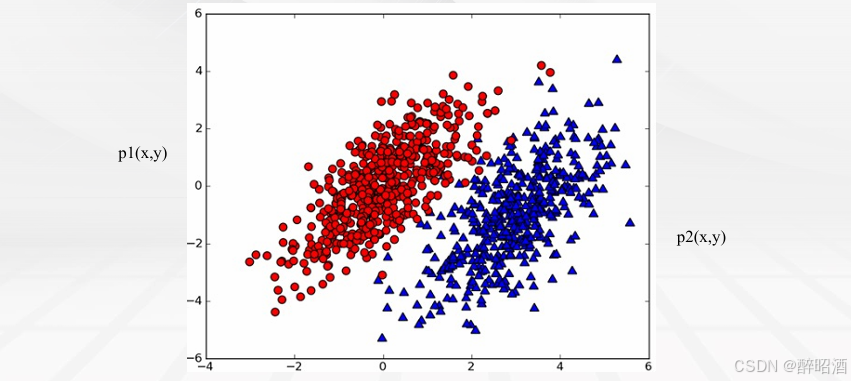
1.2逻辑回归的决策边界

• 假设有一场足球赛，我们有两支球队的所有出场球员信息、历史交锋成绩、比赛时间、主客场、裁判和天气等信息，根据这些信息预测球队的输赢。假设比赛结果记为y，赢球标记为1，输球标记为0，这个就是典型的二元分类问题，可以用逻辑回归算法来解决。

从这个例子里可以看出，逻辑回归算法的输出y∈{0,1}是个离散值，这是与线性回归算法的最大区别。

预测函数

需要找出一个预测函数模型，使其值输出在［0, 1 ］之间。然后选择一个基准值，如0.5，如果算出来的预测值大于0.5 ，就认为其预测值为1，反之则其预测值为0 。预测函数定义为：

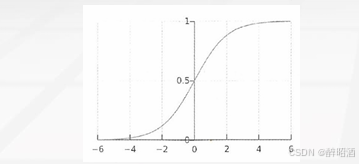
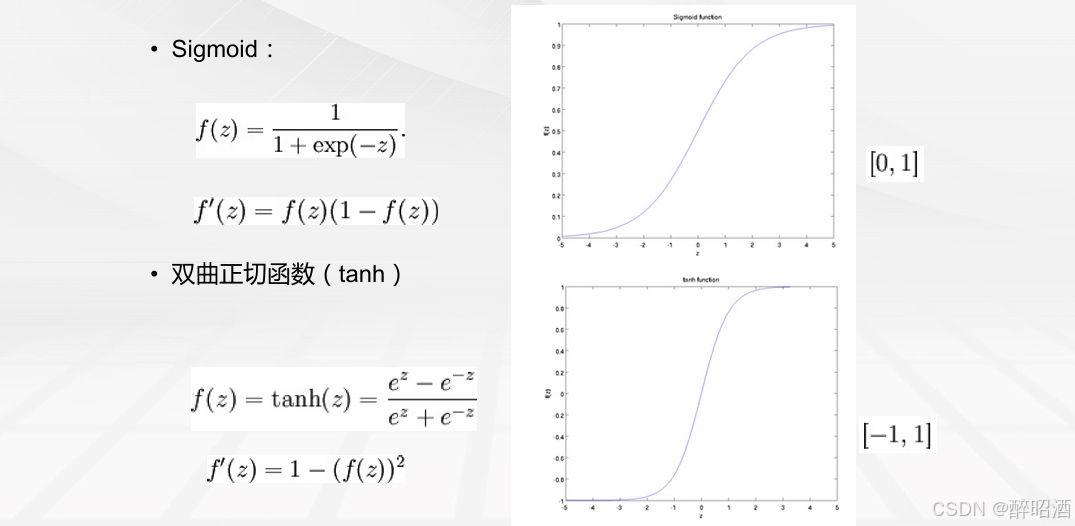
其中e是自然对数的底数。函数g(z）称为Sigmoid 函数，也称为Logistic 函数。以z为横坐标，以g(z）为纵坐标，画出的图形如下：

从图中可以看出，当z=0时，g(z)=0.5。当 z>0时，g(z)>0.5，当z越来越大时，g(z)无限接近于1。当z<0时，g(z)<0.5，当z越来越小时，g(z）无限接近于0。这正是我们想 要的针对二元分类算法的预测函数。

怎样把输入特征和预测函数结合起来呢？

结合线性回归函数的预测函数hθ(x)＝θTX ，假设令z(x)＝θTX ，则逻辑回归算法的预测函数如下：

从这个例子里可以看出，逻辑回归算法的输出y∈{0,1}是个离散值，这是与线性回归算法的最大区别。

hθ(x)表示在输入值为x，参数为θ 的前提条件下y=1的概率。用概率论的公式可以写成：

即：在输入x 及参数θ条件下y= 1的概率，这是个条件概率公式。由概率论的知识可以推导出：

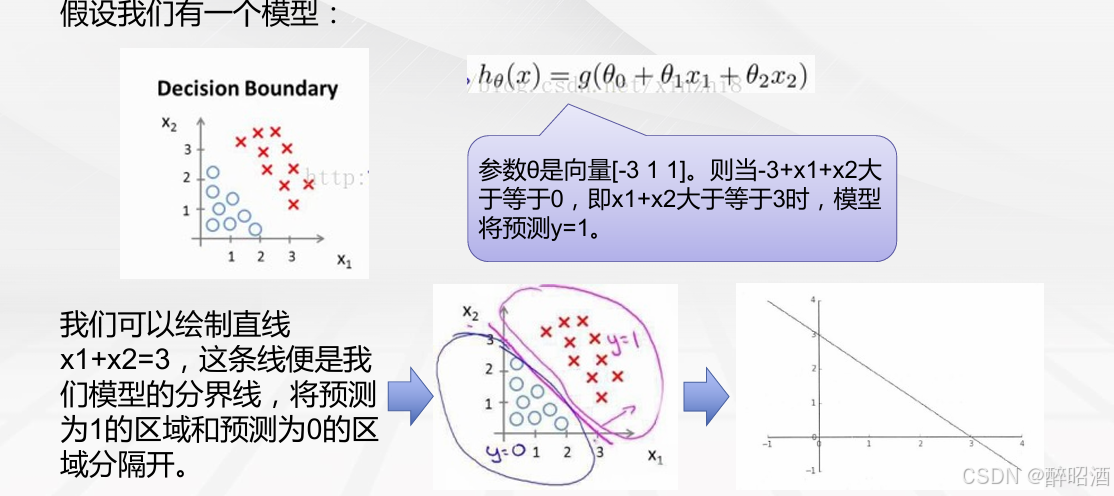
决策边界

对于逻辑回归能够解决分类问题。这里引入一个概念，叫做决策边界（decision boundary）的概念，可以理解为是用以对不同类别的数据分割的边界，边界的两旁应该是不同类别的数据。

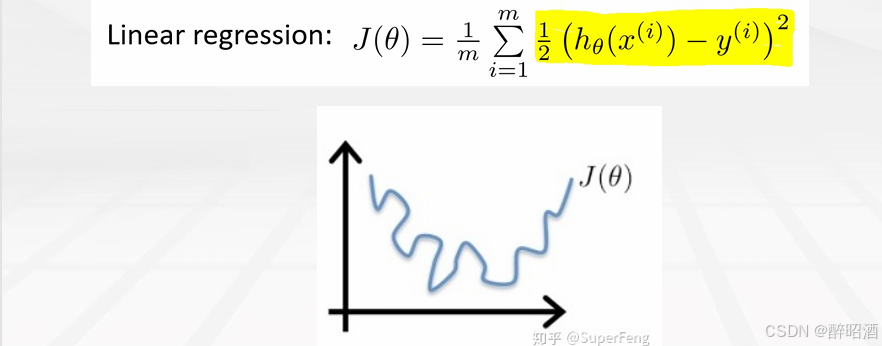
1.3逻辑回归的代价函数及梯度下降

代价函数

我们不能使用线性回归模型的代价函数来推导逻辑回归的代价函数，因为那样的代价函数太复杂，最终很可能会导致无法通过迭代找到代价函数值最小的点。

为了容易地求出代价函数的最小值，我们分成y=1和y=0两种情况来分别考虑其预测值与真实值的误差。我们先考虑最简单的情况，即计算某个样本x，y其预测值与真实值的误差，我们选择的代价函数公式如下：

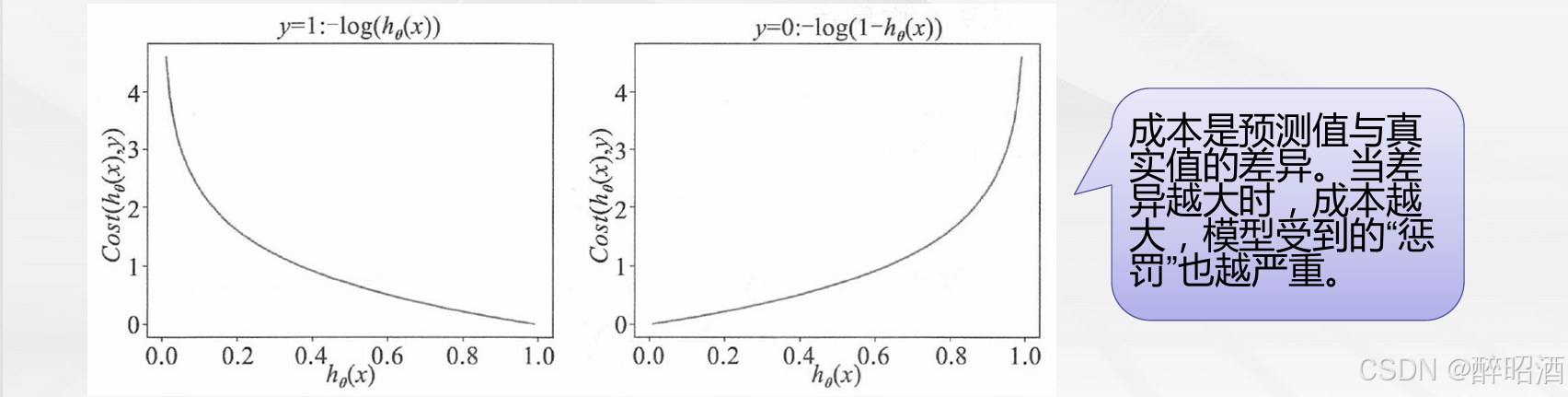
我们以hθ(x)为横坐标，以成本值Cost(hθ(x) ,y）为纵坐标，把上述两个公 式分别画在二维平面上，如下图所示。

• 在左图中，当y=1时，随着hθ(x)的值（预测为1的概率〉越来越大，预测值越来越接近真实值，其成本越来越小。

• 在右图中，当y=0时，随着hθ(x)的值（预测为1的概率）越来越大，预测值越来越偏离真实值，其成本越来越大。

思考： 符合上述规律的函数模型很多，为什么我们要选择自然对数函数来作为成本函数呢？

逻辑回归模型的预测函数是Sigmoid 函数，而Sigmoid 函数里有e的n次方运算，自然对数刚好是其逆运算，比如：log(en)＝n 。

• 选择自然对数，最终会推导出形式优美的逻辑回归模型参数的迭代函数，而不需要去涉及对数运算和指数函数运算。这就是我们选择自然对数函数来作为成本函数的原因。

更进一步，把输入值x从负无穷大到正无穷大映射到［0, 1 ］区间的模型很多，逻辑回归算法为什么要选择Sigmoid 函数作为预测函数的模型呢？

• 严格地讲，不一定非要选择Sigmoid 函数作为预测函数。但如果不选择 Sigmoid 函数，就需要重新选择性质接近的成本函数，这样才能在数学上得到既方便表达、效率又高的成本函数。

成本函数的统一写法问题:

分开表述的成本计算公式始终不方便，能不能合并成一个公式呢？考虑下面的公式：

由于y∈{0,1}是个离散值，当y = 1 时，1-y = 0 ，上式的后半部分为0 ；当y = 0 时，上式的前半部分为0 。因此上式与分开表达的成本计算公式是等价的。

根据一个样本的成本计算公式，很容易写出所有样本的成本平均值，即成本函数：

梯度下降算法

和线性回归类似，我们使用梯度下降算法来求解逻辑回归模型参数。根据梯度下降算法的定义，可以得出：

这里的关键是求解代价函数的偏导数。最终推导出来的梯度下降算法公式为：

1.4逻辑回归的正则化

我们先来看线性回归模型的成本函数是如何正则化的：

•公式中前半部分就是原来我们学过的线性回归模型的成本函数，也称为预测值与实际值的误差。

•后半部分为加λ的正则项。

其中λ的值有两个目的，即要维持对训练样本的拟合，又要避免对训练样本的过拟合。如果λ值太大，则能确保不出现过拟合，但可能会导致对现有训练样本出现欠拟合。

这样，通过调节参数λ就可以控制正则项的权重，从而避免线性回归算法过拟合。

二、朴素贝叶斯

问题引出

2.1基础知识回顾

贝叶斯分类：贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。

先验概率：根据以往经验和分析得到的概率。我们用𝑃(𝑌)来代表在没有训练 数据前假设𝑌拥有的初始概率。

后验概率：根据已经发生的事件来分析得到的概率。以𝑃(𝑌|𝑋)代表假设𝑋成立的情况下观察到𝑌数据的概率，因为它反映了在看到训练数据𝑋后𝑌成立的置信度。

联合概率：是指在多元的概率分布中多个随机变量分别满足各自条件的概率。𝑋与𝑌的联合概率表示为𝑃(𝑋,𝑌)、𝑃(𝑋𝑌)或𝑃(𝑋∩𝑌)。

假设𝑋和𝑌都服从正态分布，那么𝑃(𝑋<5,𝑌<0)就是一个联合概率，表示𝑋<5,𝑌<0两个条件同时成立的概率。表示两个事件共同发生的概率。

全概率公式：

贝叶斯公式：

朴素贝叶斯法是典型的生成学习方法。生成方法由训练数据学习联合概率分布𝑃(𝑋,𝑌)，然后求得后验概率分布𝑃(𝑌|𝑋)。

具体来说，利用训练数据学习𝑃(𝑋|𝑌)和𝑃(𝑌)的估计，得到联合概率分布：P(𝑋,𝑌)＝𝑃(𝑋|𝑌)𝑃(𝑌)

2.2基本方法

• 训练数据集：

• 由X和Y的联合概率分布P(X,Y)独立同分布产生

• 朴素贝叶斯通过训练数据集学习联合概率分布P(X,Y) ，

        •即先验概率分布：

        •及条件概率分布：

       •注意：条件概率为指数级别的参数

        •假设每个特征有Sj种取值

• 条件独立性假设：

• “朴素”贝叶斯名字由来，牺牲分类准确性。

• 贝叶斯定理：

• 代入上式：

• 贝叶斯分类器：

• 分母对所有ck都相同：

2.3参数估计

• 应用极大似然估计法估计相应的概率：

• 先验概率P(Y=ck)的极大似然估计是：

• 设第j个特征x(j)可能取值的集合为：

• 条件概率的极大似然估计：

2.4流程

2.5参数估计

• 1、计算先验概率和条件概率

• 2、对于给定的实例

• 计算

• 3、确定y的类别

2.6优缺点

• 优点：所需估计的参数少，对于缺失数据不敏感。

• 缺点：假设属性之间相互独立，这往往并不成立。（喜欢吃番茄、鸡蛋，却不喜欢吃番茄炒蛋）

三、K近邻法（KNN）

3.1K近邻

𝑘近邻法（k-Nearest Neighbor, kNN）是一种比较成熟也是最简单的机器学习算法，可以用于基本的分类与回归方法。

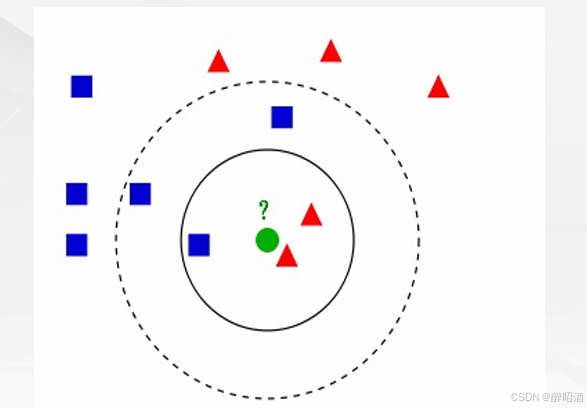
算法的主要思路：

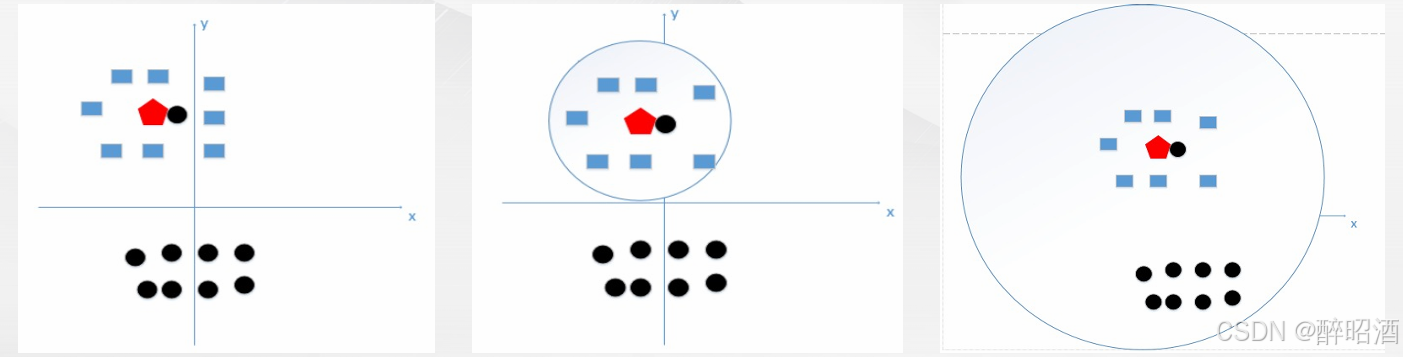
如果一个样本在特征空间中与𝑘个实例最为相似(即特征空间中最邻近)，那么这𝑘 个实例中大多数属于哪个类别，则该样本也属于这个类别。

• 对于分类问题：对新的样本，根据其𝑘个最近邻的训练样本的类别，通过多数表决等方式进行预测。

• 对于回归问题：对新的样本，根据其𝑘个最近邻的训练样本标签值的均值作为预测值。

KNN算法流程如下：

1.计算测试对象到训练集中每个对象的距离

2.按照距离的远近排序

3.选取与当前测试对象最近的k的训练对象， 作为该测试对象的邻居

4.统计这k个邻居的类别频次

5.k个邻居里频次最高的类别，即为测试对象的类别

KNN算法优点：

1.理论成熟，思想简单，既可以用来做分类又可以做回归

2.可以用于非线性分类

3.训练时间复杂度比支持向量机之类的算法低

4.和朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感

缺点：

1.计算量大，尤其是特征数非常多的时候

2.样本不平衡的时候，对稀有类别的预测准确率低

3.是慵懒散学习方法，基本上不学习，导致预测时速度比起逻辑回归之类的算法慢

4.相比决策树模型，KNN模型的可解释性不强

3.2距离度量

欧氏距离(Euclideandistance)

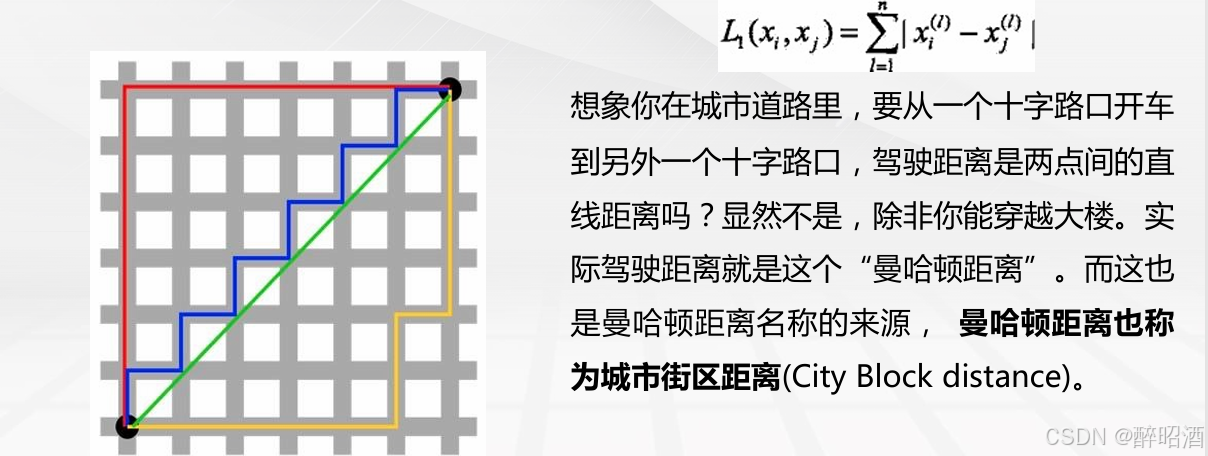
曼哈顿距离(Manhattandistance)

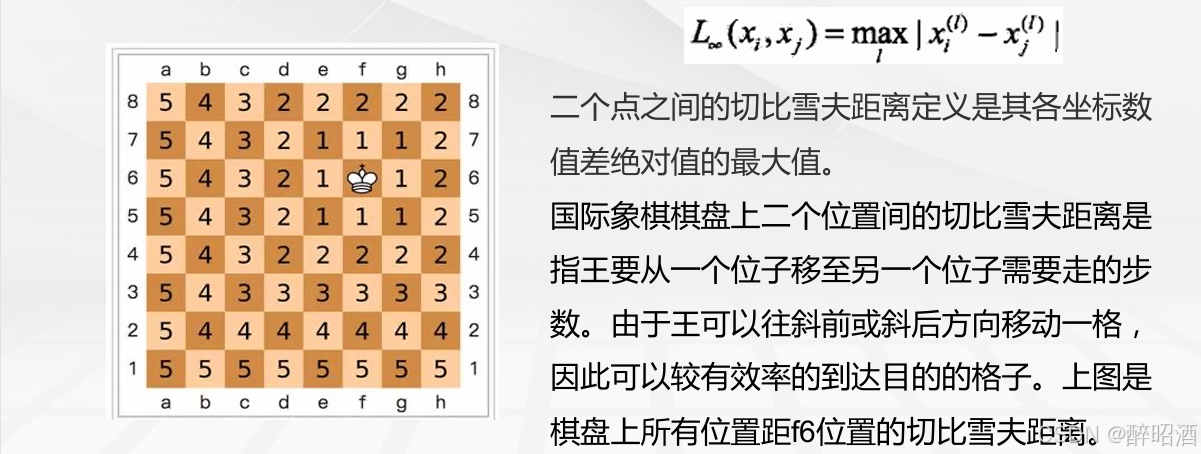
切比雪夫距离(Chebyshev distance)

闵可夫斯基距离(Minkowskidistance)

3.3K值选取与特征归一化

K值选取

除了距离的度量，在KNN算法中，K值的选取也非常重要。

K值太小，容易学到噪声，进而将输入数据判定为噪声类别；

K值太大，就相当于用较大邻域中的训练数据进行预测，这时与输入实例较远的（不相似）训练实例也会对预测起作用，使预测发生错误。

特征归一化

首先举例如下，我们用一个人身高(cm)与脚码（尺码）大小来作为特征值，类别为男性或者女性。我们现在如果有5个训练样本，分布如下：

A[(179,42),男] B[(178,43),男] C[(165,36)女] D[(177,42),男] E[(160,35),女]

现在我来了一个测试样本F(167,43)，让我们来预测他是男性还是女性，我们采取k=3来预测。下面我们用欧式距离分别算出F离训练样本的欧式距离，然后选取最近的3个，多数类别就是我们最终的结果，计算如下：

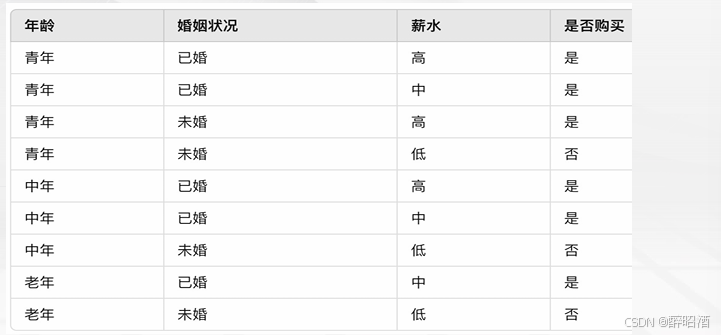
四、决策树

4.1决策树概述

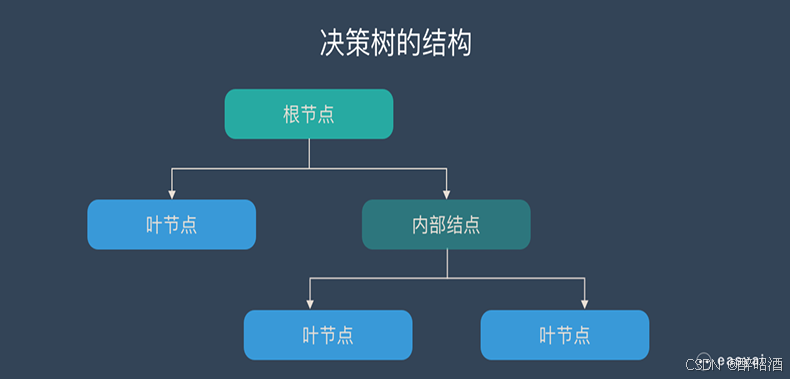
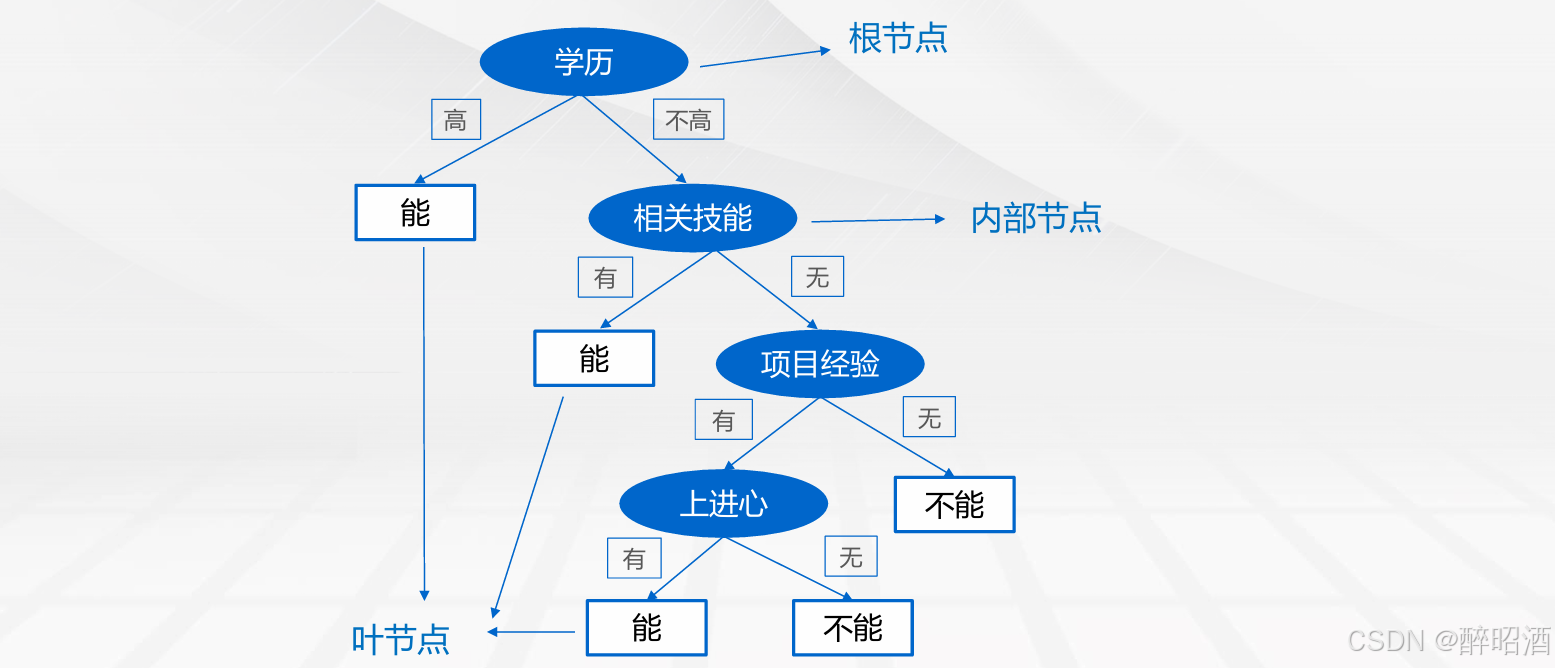
根节点：包含样本的全集

内部节点：对应特征属性测试

叶节点：代表决策结果

预测时，在树的内部节点处用某一属性值进行判断，根据判断结果决定进入哪个分支节点，直到到达叶节点处，得到分类结果。这是一种基于if-then-else 规则的有监督学习算法，决策树的这些规则通过训练得到，而不是人工制定的。

决策树的特点

优点：

1.不需要任何领域知识或参数假设。

2.适合高维数据。

3.简单易于理解。

4.短时间内处理大量数据，得到可行且效果较好的结果。

缺点：

1.容易造成过拟合，需要采用剪枝操作。

2.忽略了数据之间的相关性。

3.对于各类别样本数量不一致的数据，信息增益会偏向于那些更多数值的特征。 

决策树的三种基本类型

建立决策树的关键，即在当前状态下选择哪个属性作为分类依据。根据不同的目标函数，建立决策树主要有以下三种算法：

ID3 (Iterative Dichotomiser)、C4.5、CART(ClassificationAndRegressionTree)。

4.2ID3算法

1.ID3算法最早是由罗斯昆（J.RossQuinlan）于1975年提出的一种决策树构建算法，算法的核心是“信息熵”，期望信息越小，信息熵越大，样本纯度越低。

2.ID3算法是以信息论为基础，以信息增益为衡量标准，从而实现对数据的归纳分类。

3.ID3算法计算每个属性的信息增益，并选取具有最高增益的属性作为给定的测试属性。

其大致步骤为：

1.初始化特征集合和数据集合；

2.计算数据集合信息熵和所有特征的条件熵，选择信息增益最大的特征作为当前决策节点；

3.更新数据集合和特征集合（删除上一步使用的特征，并按照特征值来划分不同分支的数据集合）；

4.重复2，3两步，若子集只包含单一决策结果，则为分支叶子节点。

信息增益

•熵的理论解释：

•设X是一个取有限个值的离散随机变量，其概率分布为：

•则随机变量X的熵定义为：

•对数以2为底或以e为底(自然对数)，这时熵的单位分别称作比特(bit)或纳特(nat)，熵只依赖于X的分布，与X的取值无关。

• 条件熵H(Y|X)：表示在已知随机变量X的条件下随机变量Y的不确定性，定义为X给定条件下Y的条件概率分布的熵对X的数学期望：

• 当熵和条件熵中的概率由数据估计（特别是极大似然估计）得到时，所对应的熵与条件熵分别称为经验熵（empirical entropy)和经验条件熵（empirical conditional entropy )

• 定义(信息增益)：特征A对训练数据集D的信息增益，g(D，A), 定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差， 即    g(D，A)=H(D)-H(D|A)

• 信息增益表示得知特征X的信息而使得数据集的信息的不确定性减 少的程度。

• —般地，熵H(Y)与条件熵H(Y|X)之差称为互信息（mutual information)。

• 决策树学习中的信息增益等价于训练数据集中数据与特征的互信息。

信息增益的算法

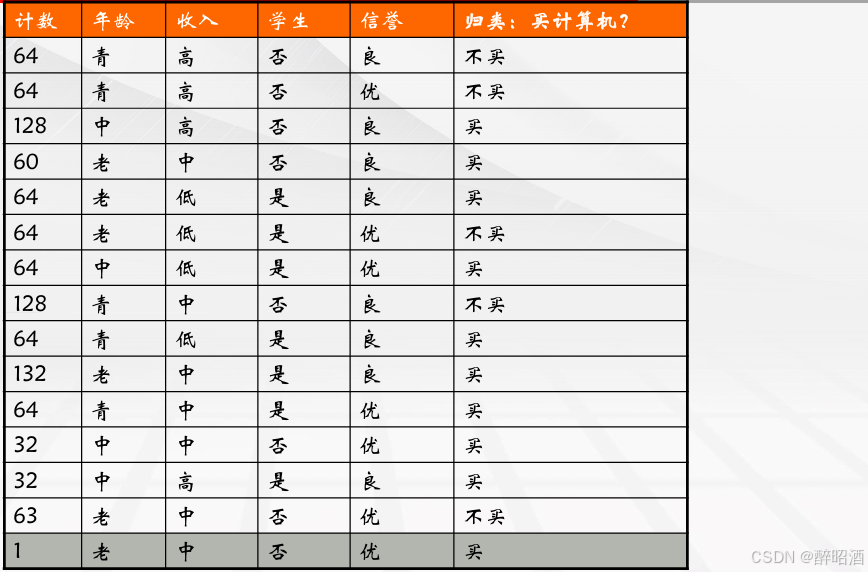
e.g.：

第1步计算决策属性的熵：

决策属性“买计算机？”。 该属性分两类：买/不买

|C1|(买)=641         |C2|（不买）= 383         |D|=|C1|+|C2|=1024

P1=641/1024=0.6260         P2=383/1024 = 0.3740

H(D)=-P1log2P1-P2log2P2 = - (P1log2P1+P2log2P2) = 0.9537

第2步计算条件属性的熵：

条件属性共有4个： 年龄、收入、学生、信誉。 分别计算不同属性的信息增 益。

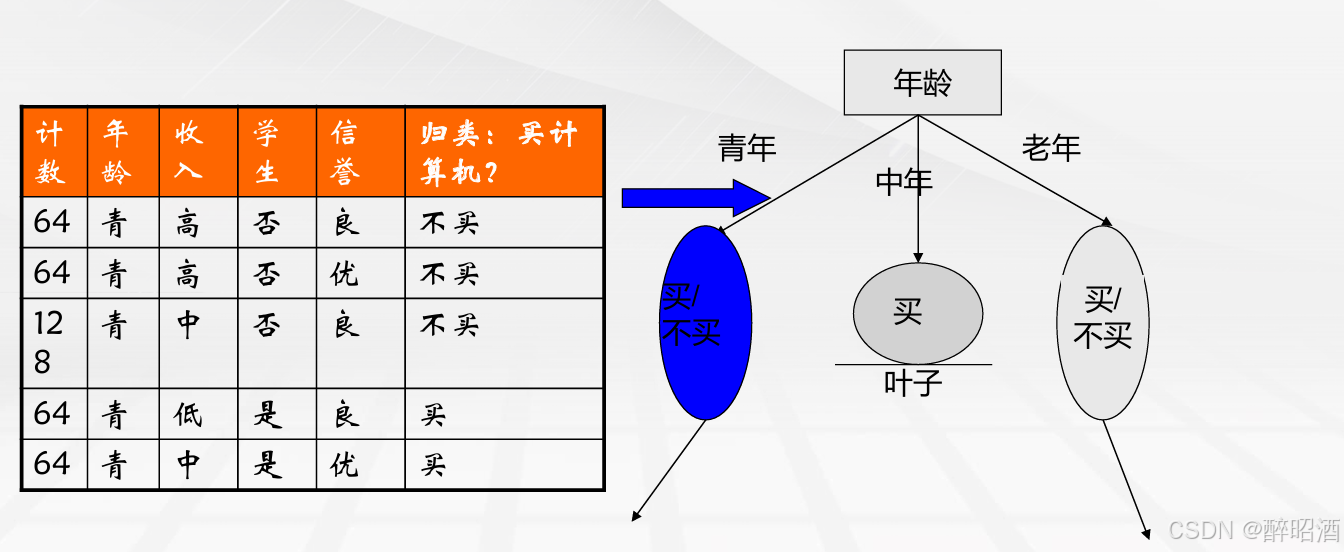
第2-1步计算年龄的熵：

年龄共分三个组： 青年、中年、老年

青年买与不买比例为128/256

|D11|(买)=128         |D12|(不买)= 256         |D1|=384

P1=128/384         P2=256/384

H(D1)=-P1log2P1-P2log2P2 = - (P1log2P1+P2log2P2) = 0.9183

第2-2步计算年龄的熵：

年龄共分三个组： 青年、中年、老年

中年买与不买比例为256/0

|D21|(买)=256         |D22|(不买)= 0         |D2|=256

P1=256/256         P2=0/256

H(D2)=-P1log2P1-P2log2P2 =-(P1log2P1+P2log2P2) =0

第2-3步计算年龄的熵:

年龄共分三个组： 青年、中年、老年

老年买与不买比例为125/127

|D31|(买)=125         |D32|（不买）=127         |D3|=|D31|+|D32|=252

P1=125/252         P2=127/252

H(D3)=-P1log2P1-P2log2P2 =-(P1log2P1+P2log2P2) =0.9157

第2-4步计算年龄的熵：

年龄共分三个组： 青年、中年、老年

所占比例：

青年组384/1025=0.375         中年组256/1024=0.25         老年组384/1024=0.375

计算年龄的平均信息期望

E（年龄）=0.375*0.9183+ 0.25*0+ 0.375*0.9157 =0.6877

G（年龄信息增益） =0.9537-0.6877 =0.2660 （1）

第3步计算收入的熵：

收入共分三个组： 高、中、低

E（收入）=0.9361

收入信息增益=0.9537-0.9361 =0.0176 (2)

第4步计算学生的熵：

学生共分二个组： 学生、非学生

E（学生）=0.7811

年龄信息增益=0.9537-0.7811 =0.1726 （3）

第5步计算信誉的熵：

信誉分二个组： 良好，优秀

E（信誉）= 0.9048

信誉信息增益=0.9537-0.9048 =0.0453 （4）

第6步计算选择节点：

年龄信息增益=0.9537-0.6877 =0.2660（1）

收入信息增益=0.9537-0.9361 =0.0176（2）

学生信息增益=0.9537-0.7811 =0.1726 （3）

信誉信息增益=0.9537-0.9048 =0.0453 （4）

缺点 ：

ID3没有剪枝策略，容易过拟合；

信息增益准则对可取值数目较多的特征有所偏好，类似“编号”的特征其信息增益接近于1；

只能用于处理离散分布的特征。

4.3C4.5算法

C4.5 算法

C4.5算法是Ross对ID3算法的改进。

• 用信息增益率来选择属性。ID3选择属性用的是子树的信息增益， 而C4.5用的是信息增益率。

• 在决策树构造过程中进行剪枝。

• 对非离散数据也能处理。

• 能够对不完整数据进行处理。

信息增益比

• 以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题

• 使用信息增益比可以对这一问题进行校正

• 定义5.3（信息增益比）特征A对训练数据集D的信息增益比定义为信息增益与训练数据集D关于特征A的值的熵之比

缺点：

• 剪枝策略可以再优化；

• C4.5 用的是多叉树，用二叉树效率更高；

• C4.5 只能用于分类；

• C4.5 使用的熵模型拥有大量耗时的对数运算，连续值还有排序运算；

• C4.5 在构造树的过程中，对数值属性值需要按照其大小进行排序，从中选择一个分割点，所以只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时，程序无法运行。

4.4CART算法

• Classification  and   Regression  Tree(CART)是决策树的一种。 

• 用基尼指数来选择属性（分类），或用均方差来选择属性（回归）。 

• 顾名思义，CART算法既可以用于创建分类树，也可以用于创建回归 树，两者在构建的过程中稍有差异。 

• 如果目标变量是离散的，称为分类树。 

• 如果目标变量是连续的，称为回归树。

（多选）下列关于ID3、C4.5和CART算法的描述中，哪些是正确的？ ( A、B、C)

A. ID3算法使用信息增益作为选择特征的标准，而C4.5算法使用信息增益比。

B. C4.5算法可以处理连续属性和缺失值，而ID3算法不能。

C. CART算法既可以用于分类问题也可以用于回归问题，而ID3和C4.5算法只能用于分类问题。

D. 所有这些算法都使用熵作为决策树构建的标准。

五、支持向量机SVM

5.1支持向量机概述

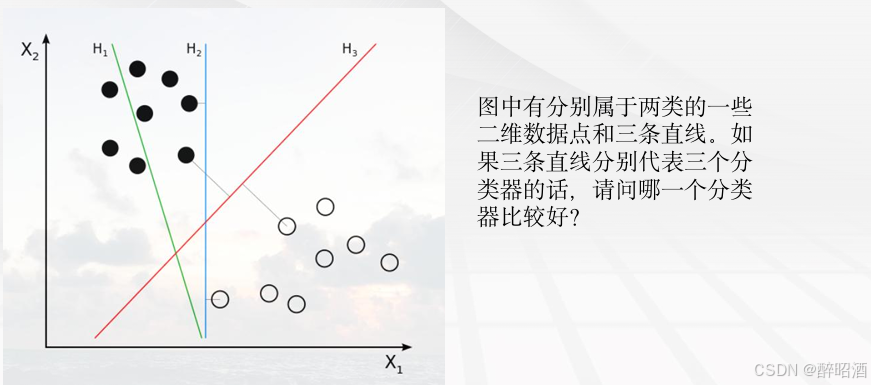
H1不能把类别分开；

H2分割线与最近的数据点只 有很小的间隔，如果测试数据有一些噪声的话可能就会被H2错误分类(即对噪声敏感、泛化能力弱)；

H3以较大间隔将它们分开， 这样就能容忍测试数据的一些噪声而正确分类，是一个泛化能力不错的分类器。

支持向量机（Support Vector Machine, SVM） 是一类按监督学习（supervised learning）方式对数据进行二元分类的广义线性分类器 （generalized linear classifier），其决策边界是对学习样本求解的最大边距超平面 （maximum-margin hyperplane） 。

与逻辑回归和神经网络相比，支持向量机，在学习复杂的非线性方程时提供了一种更为清晰，更加强大的方式。

硬间隔、软间隔和非线性 SVM

假如数据是完全的线性可分的，那么学习到的模型可以称为硬间隔支持向量机。换个说法，硬间隔指的就是完全分类准确，不能存在分类错误的情况。软间隔，就是允许一定量的样本分类错误。

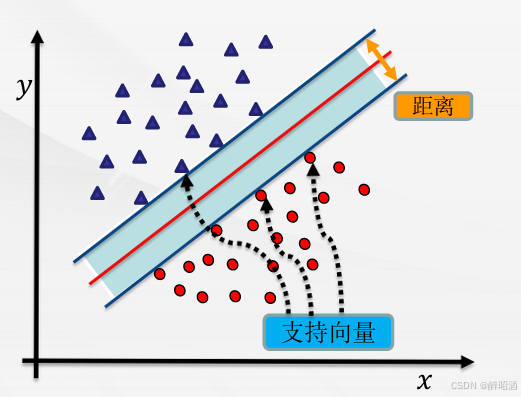
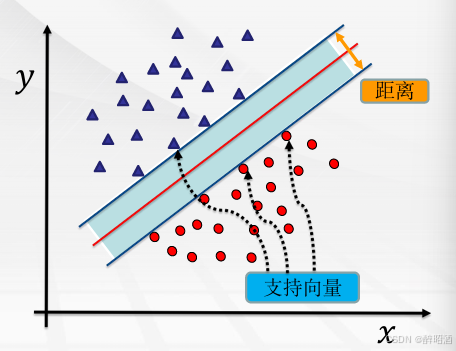
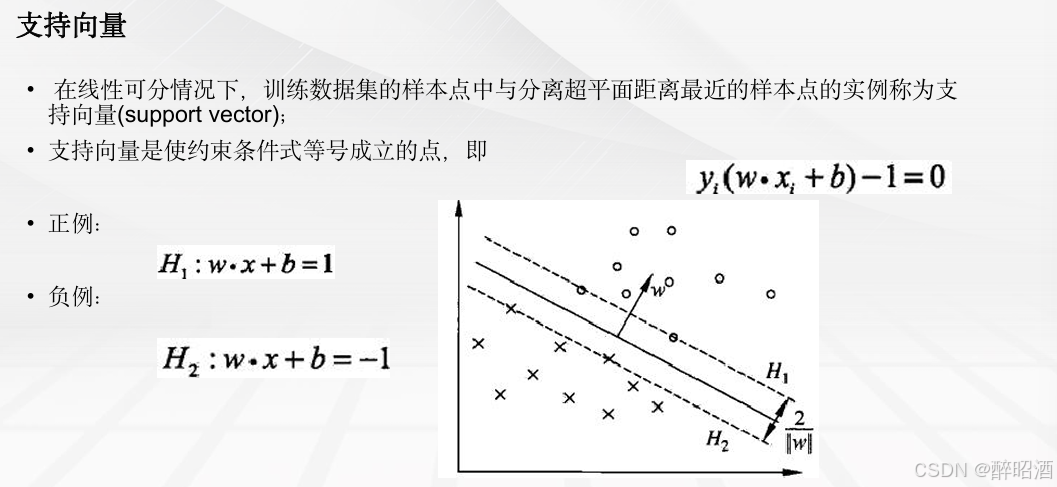
算法思想

找到集合边缘上的若干数据（称为支持向量（Support Vector））， 用这些点找出一个平面（称为决策面），使得支持向量到该平面的距离最大。

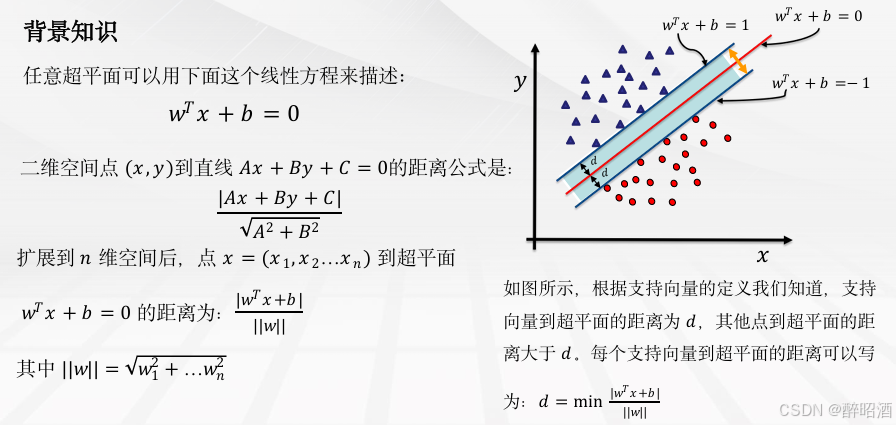
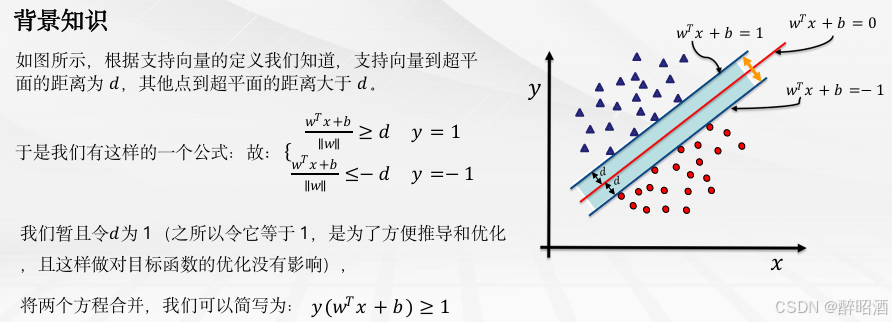
背景知识

5.2线性可分支持向量机

5.3线性支持向量机

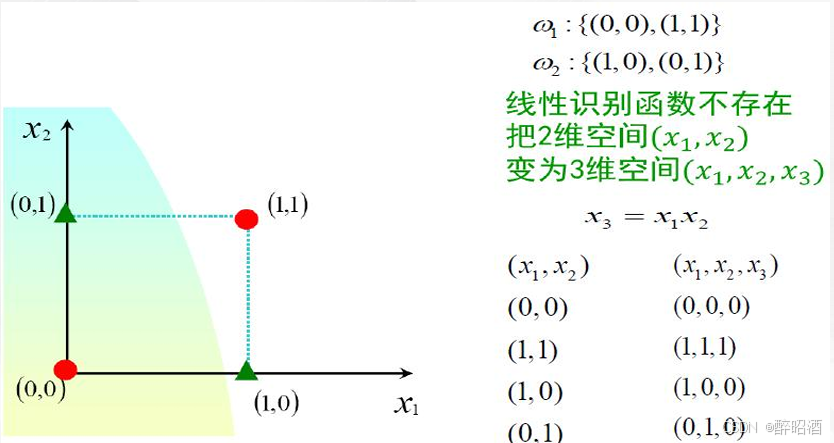
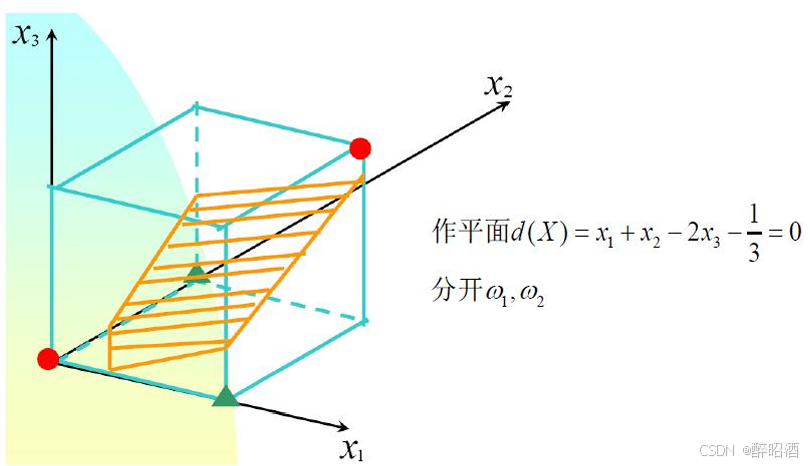
5.4线性不可分支持向量机

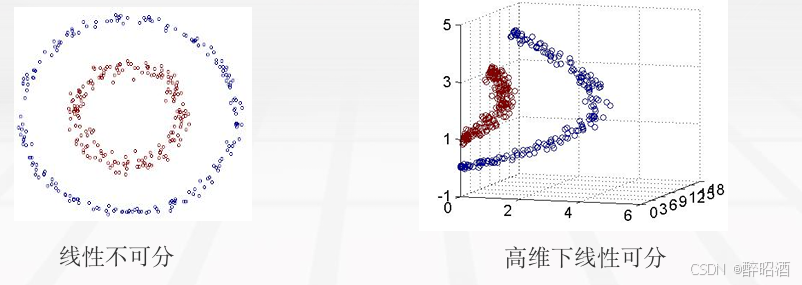
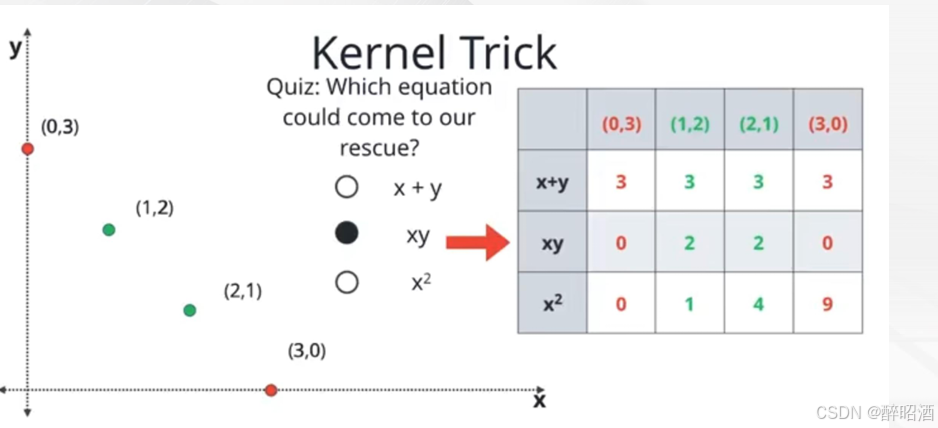
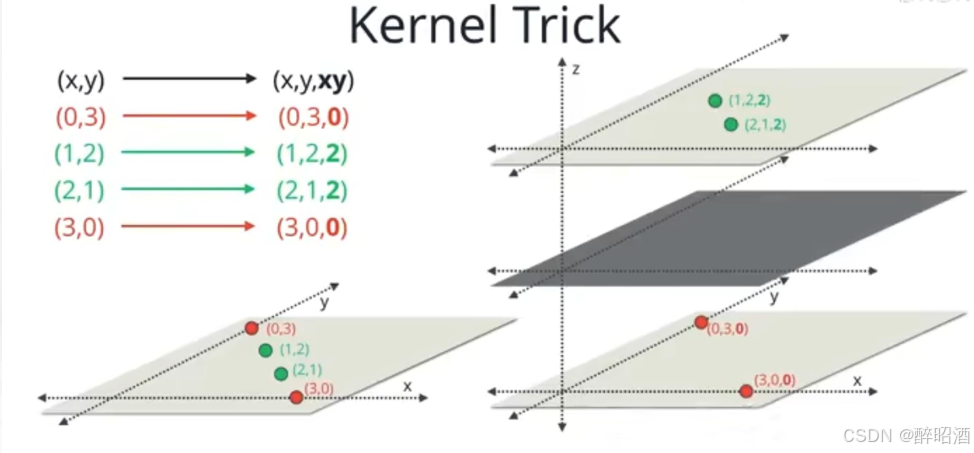
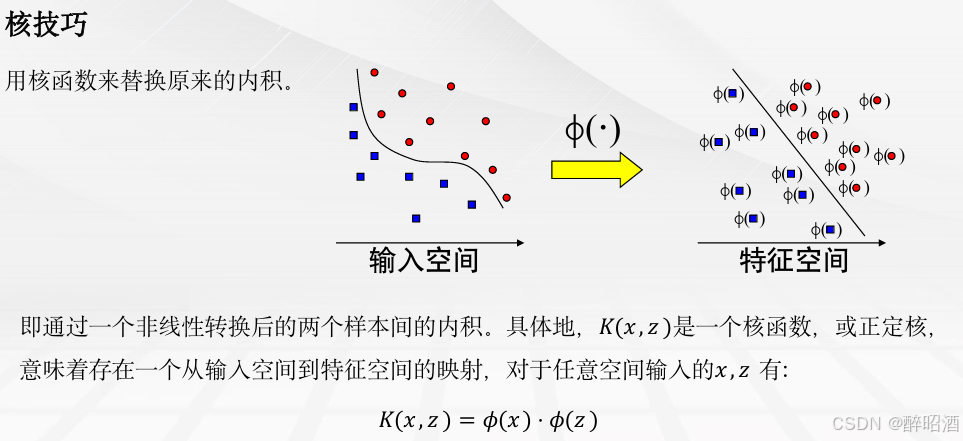
核技巧

在低维空间计算获得高维空间的计算结果，满足高维，才能在高维下线性可分。 我们需要引入一个新的概念：核函数。它可以将样本从原始空间映射到一个更高维的特质空间中，使得样本在新的空间中线性可分 。这样我们就可以使用原来的推导来进行计算，只是所有的推导是在新的空间，而不是在原来的空间中进行，即用核函数来替换当中的内积。

核技巧

5.5总结

优点:

1.由于SVM是一个凸优化问题，所以求得的解一定是全局最优而不是局部最优。

2.不仅适用于线性问题还适用于非线性问题(用核技巧)。

3.理论基础比较完善(例如神经网络就更像一个黑盒子)。

缺点:

1.二次规划问题求解将涉及m阶矩阵的计算(m为样本的个数), 因此SVM不适用于超大数据集。

2.只适用于二分类问题。(SVM的推广SVR也适用于回归问题；可以通过多个SVM的组合来解决多分类问题)

六、集成学习

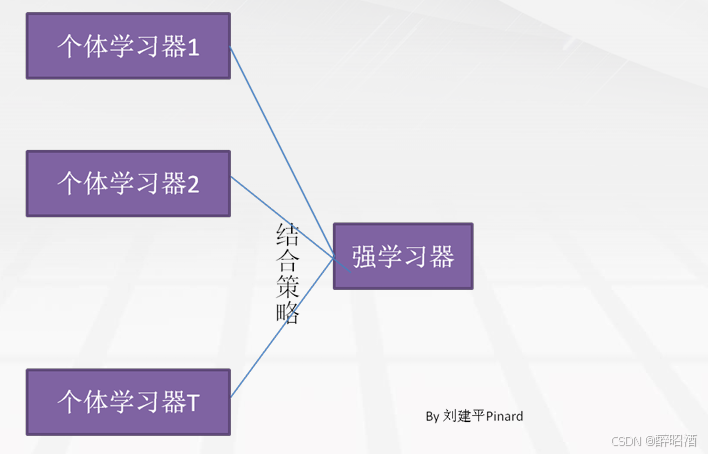
对于训练集数据，我们通过训练若干个个体学习器，通过一定的结合策略，就可以最终形成一个强学习器，以达到博采众长的目的。

集成方法分类：

序列集成方法：其中参与训练的基础学习器按照顺序生成。序列方法的原理是利用基础学习器之间的依赖关系。通过对之前训练中错误标 记的样本赋值较高的权重，可以提高整体的预测效果，代表算法为 boosting系列算法（提升法）。

并行集成方法：其中参与训练的基础学习器并行生成。并行方法的原理是利用基础学习器之间的独立性，通过平均可以显著降低错误，代表算法为Bagging系列算法（套袋法）。

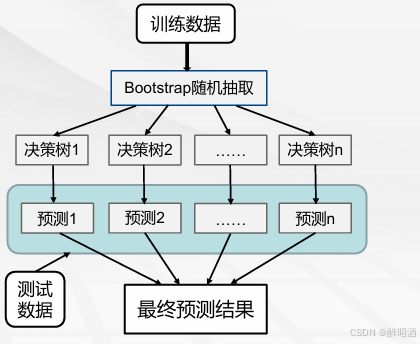
套袋法（Bagging）

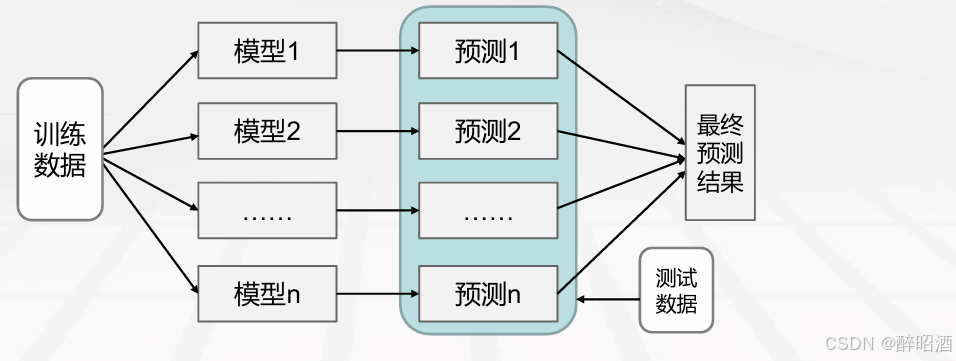
它主要对样本训练集合进行随机化抽样，通过反复的抽样训练新的模型，最终基 于这些预测模型的预测结果进行综合产生最终的预测结果。

基本思想：

1.从原始样本集中抽取训练集。每轮采取有放回的抽样从原始样本集中抽取M个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行N轮抽取，得到N个训练集。（N个训练集之间是相互独立的）

2.每次使用一个训练集得到一个模型，N个训练集共得到N个模型。（注：这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类 或回归方法，如决策树、感知器等）

3.对分类问题：将上步得到的N个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

随机森林（Random  Forest）

是Bagging 的扩展变体，它在以决策树为基学习器构建Bagging 集成的基础上，进一步在决策树的训练过程中引入了随机特征选择，因此可以概括随机森林包括四个部分： 1.随机选择样本（放回抽样）； 2.随机选择特征； 3.构建决策树； 4.随机森林投票（平均）。

• 深度太大的决策树容易受过拟合的影响。但是随机森林通过在随机特征子集上构建决策树防止过拟合，主要原因是它会对所有树的结果进行投票，从而消除了单棵树的偏差。

• 随机森林为模型增加了额外的随机性。它在分割节点时，不是搜索全部样本最重要的特征，而是在随机特征子集中搜索最佳特征。这种方式使得决策树具有多样性，从而能够得到更好的模型

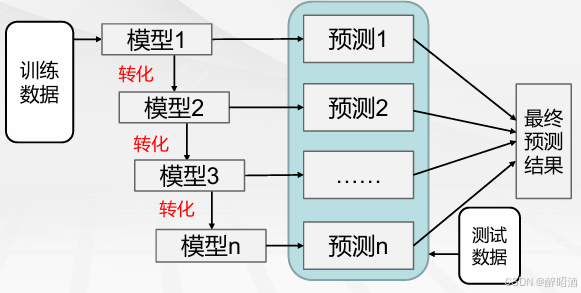
提升法（Boosting）

常用的有效的统计学习算法，属于迭代算法，它通过不断地使用一个个体学习器模型弥补前一个个体 学习模型的“不足”的过程，来串行地构造一个较强的学习器，这个强学习器能够使学习性能足够好。

常见的boosting算法：Adaboost 和梯度提升树。

基本思想：

1.利用初始训练样本集训练得到一个基学习器。

2.提高被基学习器误分的样本的权重，使得那些被错误分类的样本在下一轮训练中可以得到更大的关注，利用调整后的样本训练得到下一个基学习器。

3.重复上述步骤，直至得到N个学习器。

4.对于分类问题，采用有权重的投票方式；对于回归问题，采用加权平均得到预测值。

七、分类问题的评估指标

混淆矩阵(Confusion Matrix)：将分类问题按照真实情况与判别情况两个维度进行归类的一个矩阵，在二分类问题中，可以用一个2 ×2 的矩阵表示。

八、总结