数据库无限层级结构左右之值算法

数据库无限层级结构模型又叫嵌套集模型（Nested Set Model）是一种用于表示树状结构的数据模型，它通过左值和右值来表示树中节点的层次关系。Joe Celko在20世纪70年代首次提出了这种模型并在后来写入他的的著作《SQL for Smarties》(中文版翻译为《SQL权威指南》)中，在后来的数据库设计中得到了广泛普及和应用。

左右值的定义

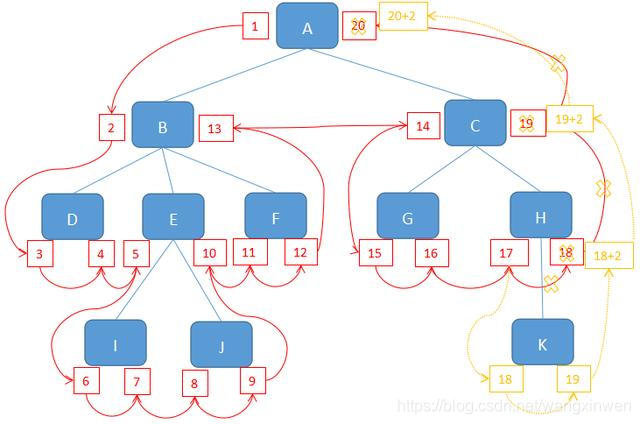
在嵌套集模型中，每个节点都有两个值，即左值（Left Value）和右值（Right Value）。左值表示节点在树中的进入顺序，右值表示节点在树中的离开顺序。通过这两个值，可以确定每个节点的子树范围、父子关系、兄弟关系等信息。

特点和优势

快速查询：通过左值和右值，可以快速确定节点的父子关系、兄弟关系等信息，从而加快了树状结构的查询速度。
空间效率：相比其他树状结构表示方法（如邻接列表、路径枚举等），嵌套集模型通常需要更少的存储空间。
简单的操作：对于嵌套集模型的节点插入、删除和移动等操作，通常只需要更新左右值，而不需要对整个树进行重组。

注意事项

更新代价：当节点插入、删除或移动时，可能需要更新树中大量节点的左值和右值，这可能会增加更新的代价。
不适用于频繁修改的树：由于更新代价较高，嵌套集模型不适用于频繁修改的树状结构，适用于静态或者修改较少的树。

SQL实例

求某节点(node)下面有多少个子孙节点

select (@node.right- @node.left -1) / 2 from tree;

求某节点(node)下面所有子孙节点

select * from tree where left>@node.left and right<@node.right order by left;

求某节点(node)所有父祖节点

select * from tree where left<@node.left and right>@node.right order by left;

在某节点(parent)下新增一节点（做为parent幼子）

update tree set right= right + 2 where right>= @parent.right;
update tree set left = left + 2 where left >= @parent.right;
insert into tree( name, left , right ) values (@name, @parent.right, @parent.right + 1);

在某节点(parent)下新增一节点（做为parent长子）

update tree set right= right + 2 where right> @parent.left ;
update tree set left = left + 2 where left > @parent.left ;
insert into tree( name, left , right ) values (@name, @parent.left + 1, @parent.left + 2);

在某节点(brother)同级左侧增加一节点(兄):

update tree set right= right + 2 where right>= @brother.right;
update tree set left = left + 2 where left>= @brother.left;
insert into tree( name, left , right ) values (@name, @brother.left, @brother.right );

在某节点(brother)同级右侧增加一节点（弟）:

update tree set right= right + 2 where right> @brother.right;
update tree set left = left + 2 where left> @brother.right;
insert into tree( name, left , right ) values (@name, @brother.right + 1, @brother.right + 2 );

删除某子节点(node)及下面孙节点:

delete from tree where left >= @node.left and right <= @node.right ;
update tree set left = left - (@node.right - @node.left + 1)  where left > @node.right;
update tree set right = right - (@node.right - @node.left + 1)  where right > @node.right;

删除某子节点(node),但不删除孙节点（孙节点上移一级）:

delete from tree where left = @node.left;
update tree set left = left - 1, right = right - 1 where left > @node.left and right < @node.right;
update tree set left = left - 2, right = right - 2 where left > @node.right;

移动节点A及下面子孙节点到节点B下面:

-- 获取节点A的左右边界值和层级
select @left_bound := left,
       @right_bound := right,
       @level := right - left + 1
from tree where id = 'A';


-- 获取节点B的右边界值
select @target_right := right from tree where id = 'B';


-- 计算节点A的移动距离
set @distance = @target_right - @left_bound;


-- 更新节点A及其子节点的左右边界值和层级
update tree
set left = case
              when left between @left_bound and @right_bound then left + @distance
              else left
           end,
    right = case
               when right between @left_bound and @right_bound then right + @distance
               else right
            end
where right >= @left_bound;

-- 更新节点A的父节点为节点B
update tree set parent_id = 'B' where id = 'A';